一种基于压缩感知的单样本人脸识别方法①

周建华

(1.湖南警察学院，湖南 长沙410138;2.湖南大学 信息科学与工程学院，湖南 长沙410082)

0 引 言

近年来，压缩感知在图像处理理论与实践方面均匀重大突破，作为一种全新的信号采样理论，采用非线性重建模型以较高质量地重构原始信号，在压缩感知框架下进行人脸识别能利用信号的稀疏结构和不相关性，可以大大提高识别效率.

1 人脸图像压缩感知过程

将人脸图像一维化成n 的离散信号x，记作x(n)，n ∈［1，2，…，N］［1］.根据信号表示变换理论，X 用一组基ΨT=［Ψ1，Ψ2，…，Ψn，…，ΨN］的线性组合表示，则

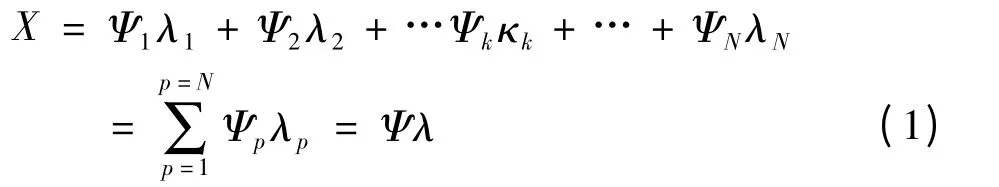
式中，λp=＜X，Ψp＞假设人脸图像信号X 在某个变换基Ψ 上有且仅有K 个大系数(其他系数等于零或者接近于零)，则认为变换基是X 上的其中一个稀疏基(可以找到图像信号多个稀疏基).如果只有k 项非零系数，而其他系数均为零，定义其图像信号为严格稀疏信号，但在复杂背景、光照及表情变化下导致拍摄人脸图像信号基本上满足不了其要求，若信号在某变换基下系数快速衰减，并呈指数级变化趋向于零，则认为该图像信号是广义上的稀疏信号(有时定义为可压缩信号)，则(1)式经压缩观测变换表示为

式中:Φ 称为测量矩阵，大小为M×N，y 为观测所得向量M×1，x 为原信号N×1(M ＜＜N)，但x 一般不是稀疏的，但在某个变换域Ψ 是稀疏的，即x=Ψθ，其中θ 为K 稀疏的，Ψ 称为变换矩阵，大小为N×N，是信号x 在Ψ 变换域的稀疏表示，即θ 只有K 项非零项.此时y=ΦΨθ，令A=ΦΨ，A 称为CS信息算子，大小为M×N，则y=Aθ.Ψ 在对拍摄的原始人脸图像进行小波变换或小波包变换得到稀疏系数按照低频、横向高频、纵向高频和斜向高频分块处理之后，在满足约束等距性RIP 条件下构建一个与小波正交基线性不相关的观测矩阵Φ，RIP性质能保证观测矩阵Φ 把两个不同的K 稀疏信号映射到同一个集合中(保证原空间到稀疏空间的一一映射关系)的概率为零，构成的条件为观测矩阵中抽取的任意M 个列向量构成的矩阵是非奇异的［2］.将人脸图像信号矩阵与观测矩阵Φ 乘积运算，经过降维计算后得到与观测矩阵维度相同的观测测量值Y 矩阵，对其小波域系数以特征点为中心进行重新排列分块，通过块稀疏的正交匹配算法BOMP 求解最优化重建恢复，其问题核心是获取测量矩阵值y 和给定观测矩阵Φ 的基础上，通过变换求解上式(2)得到原人脸图像信号矩阵X，重建过程是求解下式最优问题为

上式可通过匹配追踪算法BP、正交匹配追踪算法OMP、梯度投影算法GP 等来实现人脸模糊图像信号重建，本文考虑人脸图像分块特性，采用基于图像小波域特征点为中心的分块采样策略，分块分频率重建.上式中但我们常对将0 范数转化为1范数问题进行求解，使病态问题具体化求解［3］.

2 基于稀疏特征的冗余样本

定义三角网络人脸模型中前额、眉毛、瞳孔、眼白、耳朵、面颊、鼻子、嘴唇、下颚等特征点，通过文献［3］算法在三维网络人脸模型定位后确定其N个特征点的三维坐标并创建特征点数据库.令其对象N 个特征点υ1，υ2，…，υN，设π(υi)(i=1，2，…，M)是从输入源空间到特征目标空间的映射，设其均值为Ψ，即=Ψ(其中Ψ →0)，假定在特征目标空间中的协方差矩阵 ζ =通过λσ=ζσ 来计算ζ 的特征值λ，可变换成

由(4)、(5)、(6)综合，可得

令kij=π(υi)π(υj)，可将(4)式化简为Mλa=ka，求出其特征点特征值和向量［4］.设λ1≥λ2≥，…，≥λn按照特征显著性排列表示其m 个光照、姿态、纹理综合三维特征值，a1，a2，…，am表示其对应的三维特征向量，那么第i 个输入特征矢量在三维人脸模型空间中的降维变换表示为

将原始人脸的N 个顶点的三维模型特征点样本集表示为

图1 同一张人脸在q 取不同的值时重构的人脸图像

图2 实验选取的ORL 库人脸图像

其中X 表示其特征点光照特征向量，Y 表示其特征点姿态特征向量，Z 表示其特征点纹理特征向量.令γ 为变换组合系数，从而可以冗余生成出多个光照、表情及姿态的人脸特征表示为

令kij=π(υi)π(υj)，可将上式化简为Mλa=ka，可求出其特征点特征值和特征向量.构造训练样本为人脸样本的超完备字典，对其进行稀疏化特征表示为测试样本，寻找最佳稀疏表示自然能区分出训练样本中的不同类别［5］.取前k 个最大特征值对应的特征向量构成稀疏变换矩阵P =［p1，p2，…，pk］，根据确定K 的，其中为样本协方差矩阵的特征值.q 的取值范围为0 至1 之间，q 越大，其变换在光照、姿态、纹理等方面相似性越大，对原始人脸图像经过上述稀疏变换、块分解作为稀疏训练样本q 取不同值，对应不同特征人脸图像，如图1 所示.

3 实验过程及结果分析

本文根据上述方法，从ORL 人脸数据库中选择五个人其中任意一张人脸图像为训练样本，ORL库中剩下的其他的人脸图像(包括本人和他人的)为测试样本进行实验.选取的ORL 库人脸图像如图2 所示.

在单样本情况下，基于压缩感知和稀疏特征点，获取了更多的细节信息生成多样本人脸，通过多样本多特征匹配进行识别分类.通过10 副图像进行识别平均计算，本文所提的算法在时间复杂度上有所降低，在识别精度上大大提高，如表1 所示.

表1 几种人脸识别算法在复杂度、精确度及耗时的比较

4 结 论

本文利用压缩感知在图像处理上的优势提出的基于压缩感知单样本人脸识别方法，对原始人脸图像进行小波变换或小波包变换得到稀疏系数按照低频、横向高频、纵向高频和斜向高频分块处理之后，将人脸图像信号矩阵与观测矩阵乘积运算，得到与观测矩阵维度相同的观测测量值矩阵，在三维网络人脸模型定位后确定其显著性特征点的三维坐标，以坐标为中心点重新排列分块，通过块稀疏的正交匹配算法求解最优化重建恢复，该方法充分利用信号的稀疏结构和不相关性，大大提高人脸识别效率.

［1］ Gross R，Matthews I，Cohn J.Multi－PIE［J］.Image and Vision Computing，2010，28(5):807－813.

［2］ Chang Xueping，Zheng Zhonglong，Duan Xiaohui，et al.Sparse Representation －based Face Recognition for one Training Image Per Person［A］.Advanced Intelligent Computing Theories and Applications［C］.Berlin Heidelberg:Springer，2010:407－414.

［3］ Lu Jiwen，Tan Yap－peng，Wang Gang.Discriminative time Analysis for Face Recognition From a Single Training Sample Per Person［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence.2013，35(1):39－51.

［4］ 方红，章权兵，韦穗.基于非常稀疏随机投影的图像重建方法［J］.计算机工程与应用，2007，43(22):25－27.

［5］ 周建华.一种PCA 和SVM 多生物特征融合的视频人脸识别［J］.佳木斯大学学报(自然科学版)，2010，28(4):1－4.