关于对整系数多项式在有理数域内不可约问题的研究①

孙 慧

(吉林师范大学 数学学院，吉林 长春130000)

0 引 言

文献［1］中给出了整系数多项式在有理数域内不可约的一种判别方法—Eisenstein 判别法，此判别法仅是判别整系数多项式在有理数域上不可约的充分条件，而非必要条件.本文主要研究了一类整系数多项式虽然所给的具体形式无法应用Eisenstein 判别法，但将其进行变量替换后，则可转化成Eisenstein 判别法的应用范围.此外，还借鉴了Eisenstein 判别法的研究思路，给出了一类整系数多项式在有理数域上不可约的判别方法.

1 预备知识

定理1［1］(Eisenstein 判别法) 设f(x)=anxn+an－1xn－1+…+a1x+a0是一个整系数多项式.如果有一个素数p，使得1a0;3，那么f(x)在有理数域上是不可约的.

2 主要结果

定理2 设f(x)为一个有理系数多项式，g(x)为任意次数大于等于1 有理系数多项式，则f(x)在有理数域上可约的充分必要条件是f(g(x))在有理数域上可约.

证 充分性

若f(x)在有理数域上可约，则f(x)在有理数域上可以分解为两个次数较低的多项式的乘积.即f(x)= f1(x)f2(x)其中∂(f(x))＞ ∂(f1(x))，∂(f2(x))，将 x 换 成 g(x)可 得 f(g(x))=f1(g(x))f2(g(x))， 易 知 ∂(f(g(x))) ＞∂(f1(g(x)))，∂(f2(g(x)))，且由于g(x)为有理系数多项式，故f1(g(x))，f2(g(x))均为有理系数多项式.综上，可知f(g(x))在有理数域上可约.

必要性

若f(g(x))在有理数域上可约，则f(g(x))在有理数域上可以分解为两个次数较低的多项式的乘积.即f(g(x))=f1(g(x))f2(g(x))，其中.

∂(f(g(x)))＞∂(f1(g(x)))，∂(f2(g(x)))

由于g(x)为任意次数大于等于1 有理系数多项式，取g(x)=x，从而有f(x)=f1(x)f2(x)，易知∂(f(x))＞∂(f1(x))，∂(f2(x)).综上，f(x)在有理数域上可约.

推论2.1 设f(x)为一个有理系数多项式，g(x)为任意次数大于等于1 有理系数多项式，则f(x)在有理数域上不可约的充分必要条件是f(g(x))在有理数域上不可约.

证 推论1 为定理1 的逆否命题.

推论2.2 设f(x)为一个有理系数多项式，g(x)=ax+b，(a，b 均为有理数且a ≠0)，则f(x)在有理数域上不可约的充分必要条件是f(ax+b)在有理数域上不可约.

借鉴Eisenstein 判别法的研究思路，给出一类整系数多项式在有理数域上不可约的判别方法.

定理3 设f(x)=x4+ax3+bx2+cx+d 是一个整系数多项式.且f(x)没有有理根，如果b，c，d 均为奇数，那么f(x)在有理数域上是不可约的.

证 假设f(x)在有理数域上是可约的，由已知f(x)没有有理根，故f(x)没有一次有理因式，从而f(x)在有理数域上可分解为两个二次整系数多项式的乘积.设

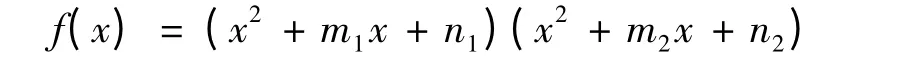
比较上面式子中x2，x 的系数及常数项有

因为d 为奇数，则n1，n2也为奇数，从而n1+n2为偶数.因为b 为奇数，由(1)可知m1m2=b－(n1+n2)为奇数，可得m1，m2也为奇数，从而m1n2+n1m2为偶数，这与c=m1n2+n1m2是奇数矛盾，从而f(x)在有理数域上是不可约的.

3 举 例

例1 证明:整系数多项式f(x)=xp+px+1(p 是奇素数)在有理数域上不可约.

证明 显然此题不能直接应用Eisenstein 判别法.令x=y－1，代入f(x)=xp+px+1，由于p是奇素数，可得

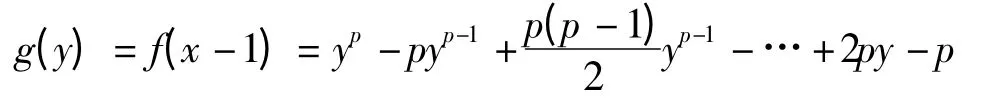
例2 证明:整系数多项式f(x)=x4+kx3+17x2+11+1(k 为奇数)在有理数域上是不可约多项式.

证明 整系数多项式f(x)在有理数域上可能的有理根为1.易知

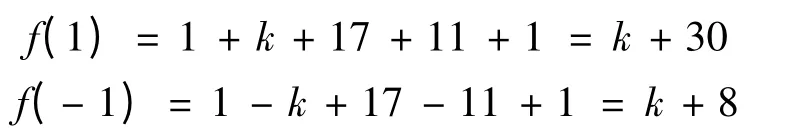
［1］ 北京大学数学系几何与代数教研室前代数小组编.高等代数［M］.北京:高等教育出版社，2003:33－34.