基于相对熵的区间型直觉模糊集多属性决策方法①

闫颖慧，祖 璇

(安徽大学数学科学学院，安徽 合肥230601)

0 引 言

随着科学技术的不断发展，我们经常会遇到一些不确定性、不精确性和模糊性问题，一般他们不能用传统的数学知识加来描述和分析.为了很好的研究和解决这些问题，学者充分的利用了模糊集理论［1～2］，区间数理论［3］，粗糙集理论［4］和概率论［5］等不确定理论，并使之得到得到了广泛的发展.后人又在这些理论的基础上进行了改进于是Atanassov［3］在1986 年首次推广了模糊集理论定义了非隶属度和犹豫度的等相关概念，同时还验证直觉模糊集的运算法则，使得该理论在解决模糊性和不确定性问题方面更具有更好的灵活性和实用性.因此最近年来有关模糊集理论的研究得到了人们的高度关注，并广泛的应用于决策、系统工程、模式识别等诸多领域.

在模糊集理论中，有关熵［10］的研究一直是一个比较重要课题.熵的类型也比较多比如模糊熵、信息熵、相对熵等等，本文基于相对熵处理区间直觉模糊集处理多属性决策出发，定义了区间型直觉模糊集的相对熵，并通过熵最小化的原理建立了非线性规划模型从而确定属性权重，同分别从隶属度、非隶属度和犹豫度三个角度出发，并根据决策者的态度引入了个参量提出了一种新的得分函数，证明了个性质.得到了区间型直觉模糊集信息环境下给出了一种有效的多属性决策方法.

1 区间型直觉模糊集的相对熵及新的得分函数

定义1［8］设X 是一个非空集合，则称A={＜x，［uAL(x)，uAU(x)］，［vAL(x)，vAU(x)］x ∈X＞}为区间直觉模糊集，其中0 ≤uAU(x)+vAU(x)≤1，uAL(x)≥0，vAL(x)≥0，则其犹豫度πA(x)=［1－uAU(x)－vAU(x)，1－uAL(x)－vAL(x)］.在实际的生活中经常会遇到决策者所给的信息是区间型，基于以前的理论定义了区间型模糊集的相对熵.

定义2 设论域X 中的两个区间直觉模糊集A和B 之间的相对熵为

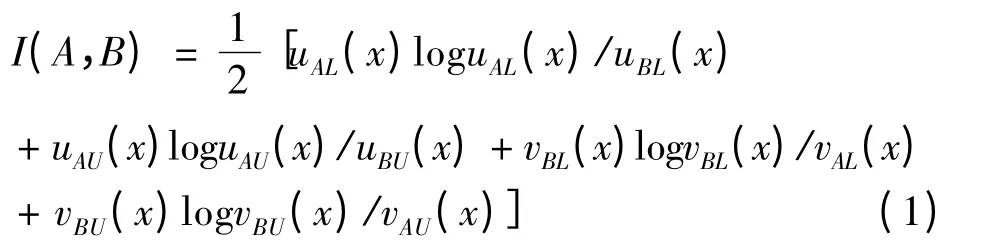
区间直觉模糊集的相对熵体现的是两个区间直觉模糊集之间的差异性，实际上它不是系统间的真正距离，在解决实际问题中可以把它看作是两者之间的距离.

性质:(1)I(A，A)=0

在区间直觉模糊集属性决策问题解决中，对对象进行综合评价，需要确定一种有效的评价标准，文献分别提出了几类得分函数［8］，但是他们没有充分考虑到犹豫度以及犹豫度的分配问题.为此本文根据决策者的态度不同犹豫度的分配也不相同基础上，引入了参量构造了一种新的得分函数.

定义3 设A={［a，b］，［c，d］}是一个区间直觉模糊集，则基于犹豫度上的得分函数为

其中λ ≥1/2.

定理1 设A，B 两个直觉模糊集，若A ⊆B，则L(A)≤L(B).

证明 不妨设A={［a1，b1］，［c1，d1］}，B={［a2，b2］，［c2，d2］}，由A ⊆B 可知a1≤a2，b1≤b2，c1≥c2，d1≥d2

证明 不妨设A={［a1，b1］，［c1，d1］}，B={［a2，b2］，［c2，d2］}，由A ⊆B 可知a1≤a2，b1≤b2，c1≥c2，d1≥d2;

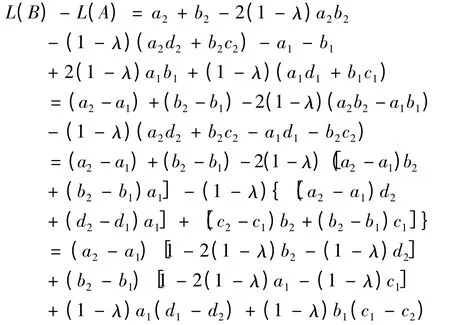
由已知条件可知

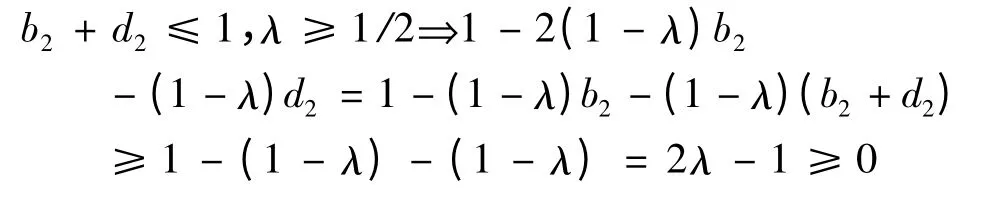
因此可以判断L(B)－L(A)≥0，即L(B)≥L(A)证毕.

直觉模糊集由模糊性和直觉性两部分构成，模糊性有隶属度和非隶属度决定的，直觉性有犹豫度决定的，上式充分的考虑了直觉性和模糊性的情况下，引入了个参量，根据决策者的态度将犹豫度合理的分配.当1/2 ≤λ ＜1 时表示决策者的态度消极;当λ=1 时决策者态度中立;当λ ＞1 时决策者态度积极.

2 属性权重未知多属性决策方法

2.1 属性权重的确定方法

对于属性权重完全未知的多属性决策问题，需要从决策信息中得到属于权重的信息，这里借鉴TOPSIS 方法的思想［9］，首先在在决策信息中提取正理 想 对 象O = (o1，o2，…，on)= {■maxaij，maxbij」，■mincij，mindij」1 ≤i ≤m，1 ≤j ≤n}.在实际生活中，如果在某个属性与正理想对象区别越小则对应的权重就应该越大反之则越小.因为相对熵可视为两者之间的距离，所以确定权重的方法就是与正理想的相对熵越小权重越大.基于此准则，可以建立如下的非线性模型:

为了解此规划模型的最优解先构造拉格朗日函数:

设则有一下函数

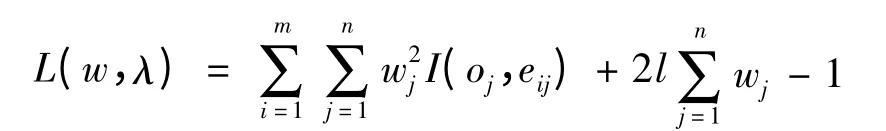
分别对wj，λ 求偏导，并令之为零可得:

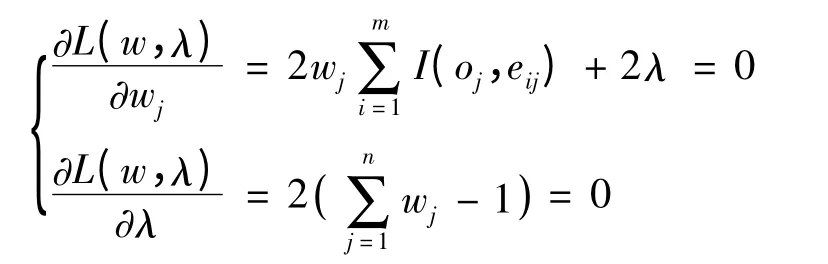
求解上述方程可得:

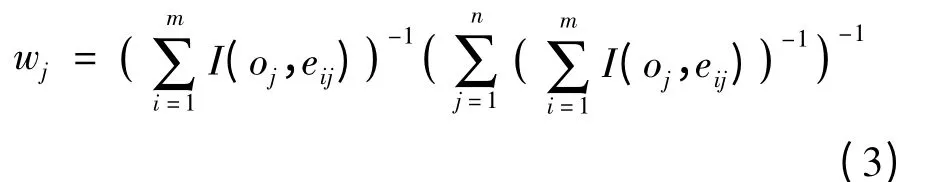
从式(3)不难看出在所有属性中，若某个属性与正理想对象的相对熵越小时对应的权重越大，相对熵越大时权重越小，满足前述准则.

2.2 决策步骤

基于上面的考虑，利用相对熵求权重，含参量犹豫度下的得分函数，结合加权算术平均算子加权几何平均算子，可以得到如下的多属性决策方法:

步骤一根据相对熵求权重的公式(3)得出各个属性的权重.

步骤二 利用加权算术平均算子或加权几何平均算子［6］计算综合区间直觉模糊集E=(E1，E2，…，Em)，其中Ei={［ai，bi］，［ci，di］};

步骤三分别利用得分函数计算得分函数值.

步骤四根据所计算的得分函数值对对象Ai进行排序.从而选出最佳对象.

3 实例分析

某公司要进行干部考核选拔，选出最佳候选人对象为此公司制定了三项考核指标aj:(a1，a2，a3)，其中文化(a1)，思想品德(a2)，领导能力(a3)然后由公司员工进行推荐从中确定4 个候选人.不妨设每位候选人在各指标下的评估信息经过处理后可表示为区间直觉模糊集的形式，决策矩阵如表1 所示:

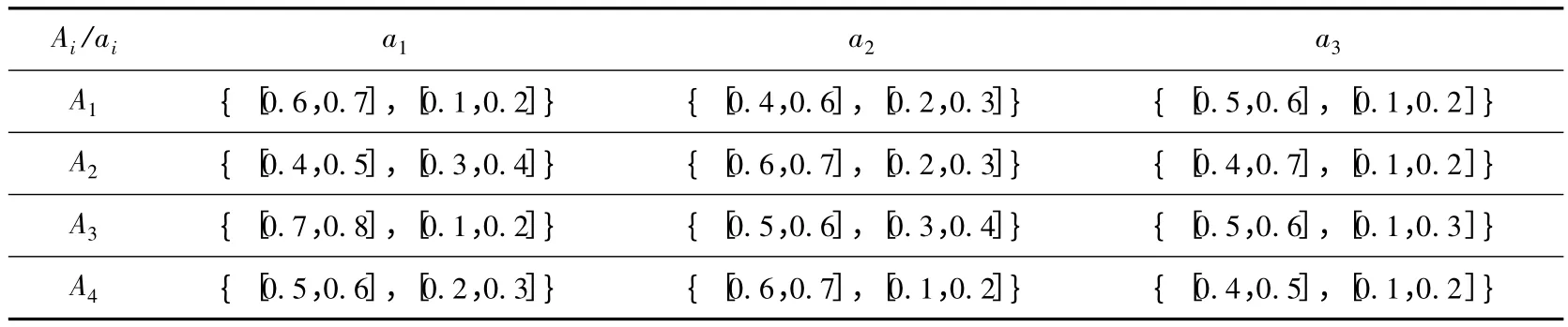
表1 决策矩阵

Step1:由公式(3)可得各属性的标准权重为w1=0.21，w2=0.23，w3=0.56

Step2:利用加权算术平均算数算子对数据进行结集可得综合区间直觉模糊集

Step3:取λ=2 即专家为积极型，利用得分函数计算可得

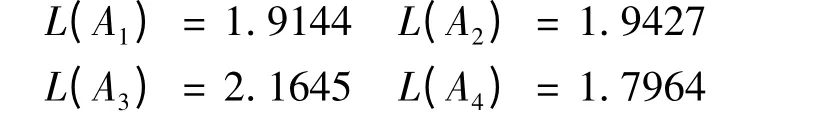
Step4:L(A3)＞L(A2)＞L(A1)＞L(A4)，从而A3＞A2＞A1＞A4即三位选人较好.

4 结束语

本文给出了一种新的求权重的方法，并且结合决策者的类型基于犹豫度的基础上引进了参数给出了度量区间型直觉模糊集的一种新的得分函数.然后结合加权算术平均算子，给出了处理多属性区间直觉模糊集信息的方法，最后结合实例说明了这种方法可以直接应用到综合评价的问题中，具有很好的应用前景.

［1］ Zadeh LA.Fuzzy sets［J］.Information and Control，1965，8(3):338－353.

［2］ 徐泽水.不确定多属性决策方法与应用［M］.北京:清华大学出版社，2005.

［3］ Atanassov K.Intuitionistic Fuzzy Sets［J］.Fuzzy Sets and Systems，1986，20(1):87－96.

［4］ Pawlak Z.Rough sets［J］.International Journal of Information and Computer Sciences，1982，11:341－356.

［5］ 缪柏其，胡太忠.概率论教程(第二版)［M］.合肥:中国科学技术大学出版社，2009.

［6］ 徐泽水.直觉模糊信息的集成方法以及在决策中的应用［J］.控制与决策，2007，22(2):215－219.

［7］ 徐泽水.直觉模糊偏好下的多属性决策途径［J］.系统工程理论与实践，2007，(11):62－70.

［8］ 姚登宝，毛军军，查道丽等 基于犹豫度下区间直觉模糊信息的决策方法及其应用［J］.合肥学院学报，2011，3(21):1－4.

［9］ 朱芳霞，陈华友.确定区间数决策矩阵属性权重的方法－－熵值法［J］.安徽大学学报:自然科学版，2006，23(1):13－19.

［10］ 冯向前，钱钢.基于熵权的区间数多属性决策方法［J］.计算机工程与应用，2010，46(33):236－238.

［11］ 王泽炎，王春霞，张金辉.一种基于理想区间数和熵的多指标评价法［J］.工程数学学报，2006，23(1):13－19.