运用信息论对于传统和精益生产信息流的考察①

杨国峰

(同济大学汽车学院，上海201804)

传统大规模生产系统和精益生产系统其基本理念和理论背景有着很大的不同.区别它们最重要的特征表现在对信息的传递和处理方面.20 世纪50 年代以后，社会进入了一个市场需求多样化发展的新阶段，要求工业生产向多品种，小批量方向发展.为了顺应时代要求，由丰田汽车首创的精益生产系统被创造出来.与传统生产企业采用的通过削减材料、人工、投资等可见财务项目以达到成本控制的手段不同，精益生产企业更致力于消除普遍存在但又被忽视的隐形成本，例如信息传递和沟通的成本.在企业中，此类隐形成本并非真的隐形，只是由于难以量化而被忽视.下面运用信息论的方法，对传统大规模生产系统和精益生产系统中的信息产生和传递进行研究，并量化评价两者的区别.

1 信息论基础

信息论(Information theory)由美国数学家克劳德?香农于1948 年创立，是运用概率论与数理统计的方法研究信息，信息熵，通信系统，数据传输，密码学，数据压缩等问题的应用数学学科［1］.

信息熵:自信息的数学期望.是从整个集合的统计特性来考虑的信源的平均信息量水平，代表总体特征.H 是p1，p2，…，pn的n 元函数，p 为事件的先验概率.表示成:

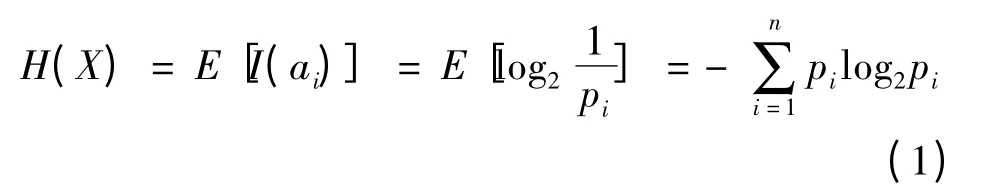
信息熵对于理解信息的价值和作用非常重要，代表了信源输出后每个消息所提供的平均信息量，或信源输出前的平均不确定度.信息熵越大，系统的不确定也越大.对于特定的系统，其信息熵是一个确定的数值［2］.

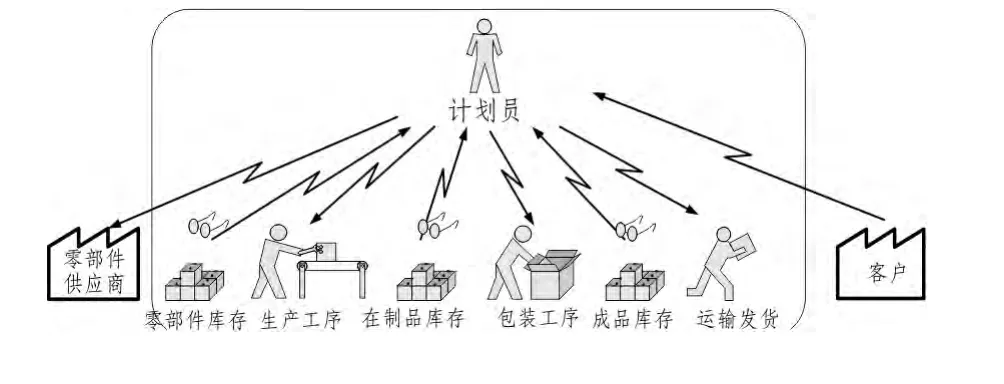
图1 传统大规模生产系统生产工序过程中的信息传递

2 传统生产系统和精益生产系统中的信息传递与处理

信息论认为，任何系统都是通过获取、传递、加工与处理信息而实现其有目的的运动的［1］，生产系统也不例外.以一个产品的生产工序过程为例，通过研究在传统生产系统中和精益生产系统中信息如何传递、变换和反馈;分析和计算的信源、信息传递路径和信息熵变化;以此来比较不同生产系统之间的信息传递效率.

传统大规模生产系统中设定的规则及其信息传递路径绘制如下:各道工序均听从计划员指令进行工作，各道工序完成指令后将停止工作直到接到新的指令.各工序间设有库存点，库存点没有最大最小储存量规定.客户向计划员发送不同数量产品的订单进行订货.其订单概率分布情况是:其中25%的订单产品数量为1，50%的订单产品数量为2，25%的订单产品数量为3.假设计划员可向各工序(包括零部件供应商)发布三种可能的指令:操作/生产产品数量1，操作/生产产品数量2，操作/生产产品数量3.

观察该系统可知，共8 条信息传递路径，分别计算其信息熵如下:

(1)客户→计划员的信息传递路径(共1 条).该信源的信息熵为:H(x)= (1/4)×log24 +(1/2)×log22+(1/4)×log24=1.5 比特/事件.

(2)计划员→各工序(运输发货，包装工序，生产工序，零部件供应商)的信息传递路径(共4条).其各事件概率ppx未知(因为各工序间库存未知，生产数量与客户订单数量可能不同)，此处简化推断为均匀概率，即:ppx1=ppx2=ppx3=1/3.则该类信源的信息熵为:H(x)=(1/3)×log23 +(1/3)×log23+(1/3)×log23 ≈1.58 比特/事件.

(3)各库存点→＞计划员的信息传递路径(共3 条).在传统大规模生产系统中，库存点所存放产品数量通常没有设置最高和最低值，因此其产品数量可以为0 至n(n 受限于存放点的实际储存条件)，这里将≥3 件产品的存放事件归为一类，并简化认为各库存点的概率分布相同.则该类信源的信息熵为:H(x)=(1/4)×log24+(1/2)×log22+(1/8)×log28+(1/8)×log28=1.75 比特/事件.

当客户下达订单时，系统通过上述8 条信息传递路径的信息传递所产生的信息熵量化变化如表1 所示.根据信息熵可加性的基本性质，汇总后可得，其信息熵总量变化为13.07 比特/事件.

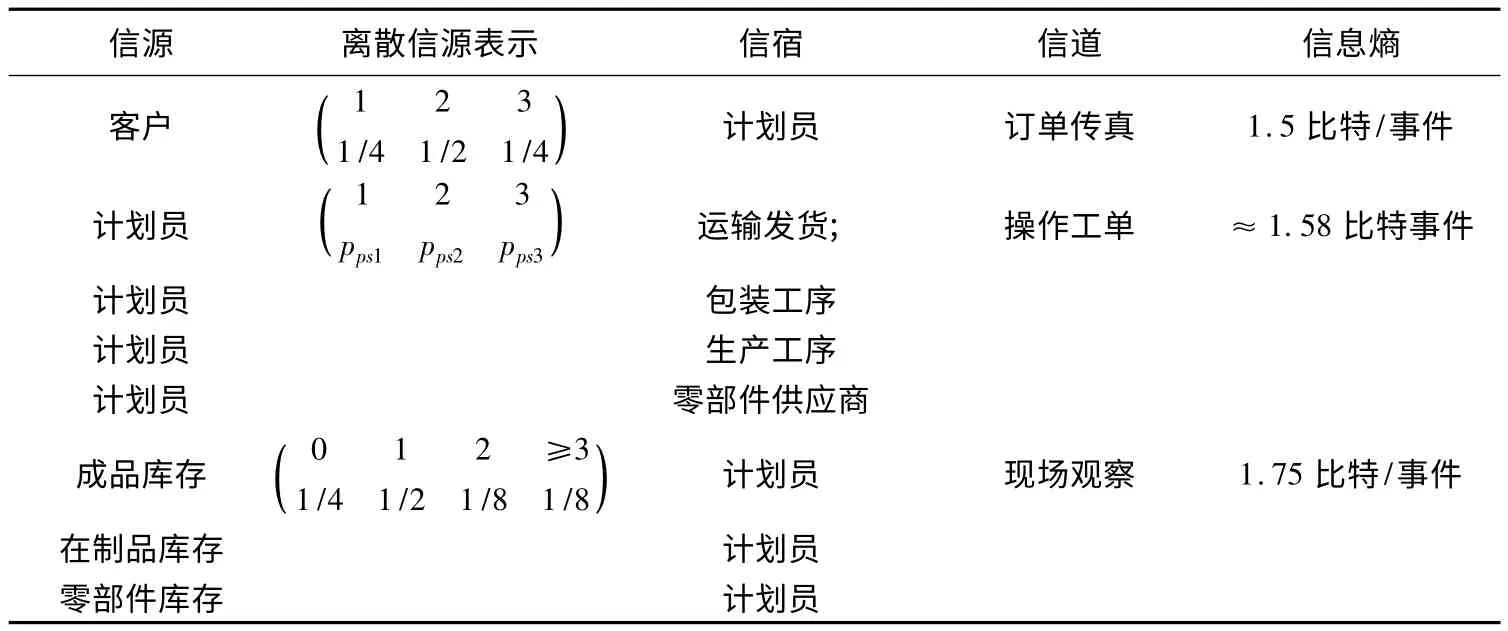
表1 传统生产系统中信息传递所产生的信息熵变化量

同样的生产工序过程，考察其在精益生产系统中的典型信息传递，绘制如下:

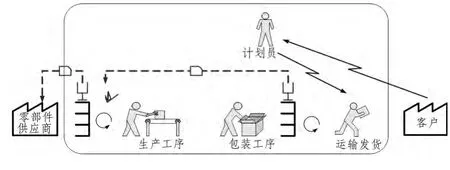
图2 精益生产系统生产工序过程中的信息传递

精益生产系统中设定的规则:计划员仅向运输发货工序发出工作指令，其余各道工序在接到生产看板时进行工作，完成生产看板后将停止工作直到新的看板出现.零部件供应商与生产工序之间设有原料超市，包装工序与运输发货之间设有成品超市.各超市遵循先进先出原则，有最大最小储存量规定.外部条件不变，客户向计划员发送相同概率分布的不同数量产品订单进行订货.计划员可向运输发货工序发布三种可能的指令:发送产品数量1，发送产品数量2，发送产品数量3.

观察该系统可知，共5 条信息传递路径，分别计算其信息熵如下:

(1)客户→计划员的信息传递路径(共1 条).该信源的信息熵为:H(x)= (1/4)×log24 +(1/2)×log22+(1/4)×log24=1.5 比特/事件.

(2)计划员→运输发货工序的信息传递路径(共1 条).此处事件概率ppx 可以简化推断为同产品数量下客户订单概率(假定产品超市的最小储存量可以满足至少一次出货要求)，即:ppx1=1/4，ppx2=1/2，ppx3=1/4.则该类信源的信息熵为:H(x)=(1/4)×log24+(1/2)×log22+(1/4)×log24=1.5 比特/事件.

(3)看板→其余工序(零部件供应商，生产工序，包装工序)的信息传递路径(共3 条).运输出货完成后，成品看板将随空箱流转至生产工序处触发产品生产，生产工序提取零部件，将零部件看板返回至零部件供应商处触发零部件生产.其中，看板的流转物理上是由物料员完成，但是物料员不接触看板所包含的信息，所以物料员在这里是信道的作用.而看板所能触发的信息只有两种:有看板时生产，无看板时不生产.其事件概率pcx未知，根据最大离散熵定理(等概率即pi=1/n 时熵最大)，则该类信源的信息熵为:H(x)＜(1/2)×log22+(1/2)×log22=1 比特/事件.

当外部事件(客户下达订单)发生时，系统通过上述5 条信息传递路径的信息传递所产生的信息熵量化变化如表2 所示.根据信息熵可加性的基本性质，汇总后可得，其系统信息熵总量变化为6比特/事件.

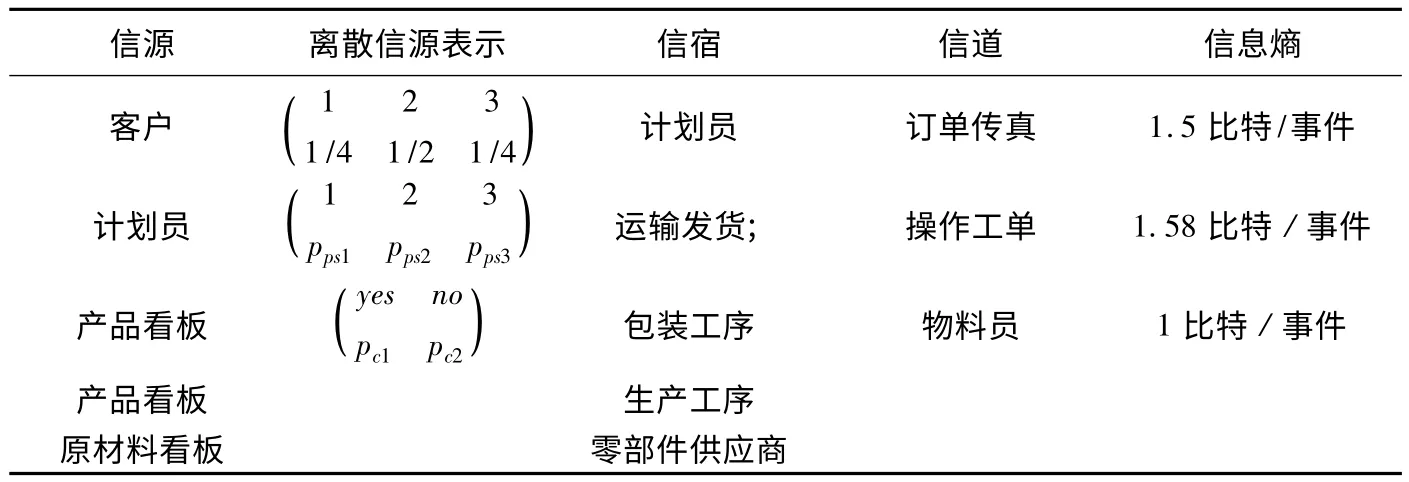
表2 传统生产系统中信息传递所产生的信息熵变化量

对比两个系统在同一个外部信息触发下的不 同信息传递以及所发生的信息熵变化如表3 所示:

表3 传统生产与精益生产系统中信息传递所产生的信息熵变化量对比

上表中可以看到，本例中传统生产系统比精益生产系统对应相同环境信息(如客户订单)做出反应需要维护和提取更多信息，精益生产系统在信息总量有效传递方面有明显优势.考虑两个系统各自增加一个工序n 的情况，在精益生产系统中，需要增加1 条信息传递:看板→工序n，系统熵增加1 比特/事件.在传统生产系统中，需要增加2 条信息传递:计划员→工序n 以及工序n 前库存→计划员，系统熵增加1.58+1.75=3.33 比特/事件.可以看到，在系统扩展性方面，增加一个子系统环节，传统生产系统的信息熵增加值是精益生产系统的三倍以上.

3 结 语

综上所述，精益生产系统与传统生产系统相比，精益生产系统在信息传递方面的效率更高.在同等系统内外部条件下，完成同样产出，所需产生和使用的信息熵只有后者的一半，同时信息的信源和信宿分布更均匀.精益生产系统更重要的优势则是在系统扩展性方面，同样的子系统增加所需的信息熵增加是传统生产系统的三分之一.由此可得，产品本身越复杂，精益生产系统在信息传递和处理方面的优势则越大.

［1］ 田宝玉，杨洁，贺志强，王晓湘.信息论基础［M］.北京:人民邮电出版社，2008:26－28.

［2］ 段建国，李爱平，谢楠，徐立云.基于状态熵的制造系统结构复杂性建模与评价［J］.机械工程学报，2012，48(5):92－100.

［3］ 曹雪虹.信息论与编码［M］.北京:清华大学出版社，2009.

［4］ 詹姆斯，格雷克著，高博译.信息简史［M］.北京:人民邮电出版社，2008.