关于大气中PM2.5浓度的综合预测

谢心庆，许英

(新疆财经大学应用数学学院，新疆乌鲁木齐 830012)

关于大气中PM2.5浓度的综合预测

谢心庆，许英

(新疆财经大学应用数学学院，新疆乌鲁木齐 830012)

鉴于PM2.5对人体的危害，为了提前预测PM2.5浓度值并及时通过降雨方法降低其浓度，开展了PM2.5浓度综合预测研究。通过对西安市一个空气质量监测点收集到观测数据分析与PM2.5浓度强相关的因素，随后综合考虑天气、温度、风力风向对PM2.5浓度观测值的影响，通过添加虚拟变量及因子分析提取因子的方法，将强相关因素、提取的天气、温度、风力风向因子与PM2.5浓度观测值进行回归预测，最终得到较好预测效果。

PM2.5;虚拟变量;因子分析;多元回归

0 引言

2013年7月12日《中国新闻网》报道:“2013年初以来，中国发生大范围持续雾霾天气。据统计，受影响雾霾区域包括华北平原、黄淮、江淮、江汉、江南、华南北部等地区，受影响面积约占国土面积的1/4，受影响人口约6亿人”。在北美和欧洲研究人员对环境颗粒物对人体的危害做了广泛的流行病学研究［1－6］。对于颗粒物PM2.5(空气质量标准中颗粒粒径小于等于2.5μm浓度限值)可以进入人体的下呼吸道，通过液泡进入血液，对人体肺功能及生长发育的儿童有严重危害［7］。因此，若是对PM2.5浓度值在模型上有很好的预测，便可应用人工降雨或降雪等方式减少污染。

近年来，我国雾霾现象的出现主要来源于二次颗粒物(即通过与大气组成成分发生化学反应后生成的颗粒物)。形成 PM2.5的前体物包括:SO2、NOx、挥发性有机化合物(VOCS)、NH3等。但由于PM2.5进入研究视线较短，综合考虑天气、温度、风力风向的PM2.5综合预测研究较少［8］。

1 PM2.5相关因素分析

对西安市一个空气质量监测点(高压开关厂) 2013年3月至4月间采集的SO2、NO2、可吸入颗粒物(PM10)、CO、臭氧、PM2.5、空气质量指数等数据进行分析，并根据相关分析方法判断哪些因素与PM2.5浓度值强相关，结果见表1。

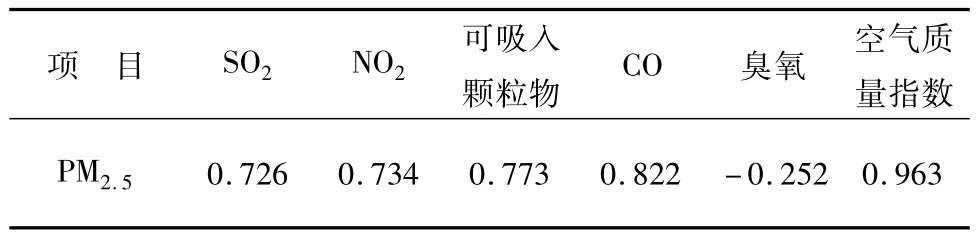
表1 各观测数据与PM2.5相关系数分析

从表1可以看出，除臭氧浓度与PM2.5浓度值相关性不大，其余各因素 SO2、NO2、可吸入颗粒物(PM10)、CO的浓度均与PM2.5浓度值强相关。

2 虚拟变量的选定

2.1 虚拟变量的数据处理［9］

为了考虑天气、温度、风力风向对PM2.5浓度值变化的影响，先将天气、温度、风力的变量数值化进行以下处理:

对于天气，将天气变量设为Dij(i=1，2;j=1，2，3…6)，i=1代表白天，i=2代表夜间;j=1，2，3…6分别代表晴、阴、雨、多云、浮尘、雪等天气。

D的取值为1和0，1代表是，0代表不是。

对于温度，将温度变量设为Ti(i=1，2)，i=1代表一天的最高温度;i=2代表一天的最低温度。

对于风力，将风力变量设为Wij(i=1，2;j=1，2，3…9)，i=1代表白天，i=2代表夜间;j=1，2，3…9分别代表北风、东北风、东风、东南风、南风、西南风、西风、西北风、最大风力。其中，除最大风力值为具体数值外，其余Wij取值为1和0，1代表是，0代表不是。

2.2 方差分析

为了辨别天气、风向对PM2.5浓度值变化的影响，首先应用方差分析方法分析天气、风向对PM2.5浓度值变化是否有显著性影响，结果见表1～9。

对于天气，将天气变量设为Di(i=1，2，…，6)，Di=i分别代表晴、阴、雨、多云、浮尘、雪等天气。

表2 白天天气情况对PM2.5浓度值变化的分析结果

表3 方差分析(单因素方差分析)

从表2、3中P=0.453＞α=0.05，可以看出白天天气情况对PM2.5浓度值变化没有显著性差异。

表4 夜间天气情况对PM2.5浓度值变化的分析

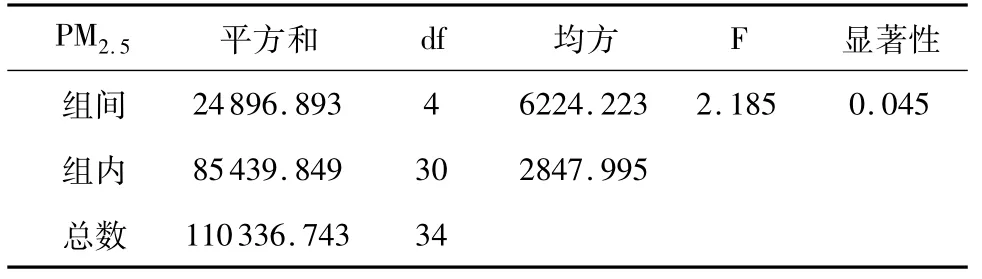
表5 方差分析(单因素方差分析)

从表4、5中P=0.045＜α=0.05，可以看出白天天气情况对PM2.5浓度值变化存在显著性差异。

对于风向，将风向变量设为Wi(i=1，2，…，8)，Wi=i分别代表北风、东北风、东风、东南风、南风、西南风、西风、西北风等风向。

表6 白天风向情况对PM2.5浓度值变化的分析

从表6、7中P=0.039＜α=0.05，可以看出白天风向情况对大气中PM2.5浓度值的变化存在着显著性差异。

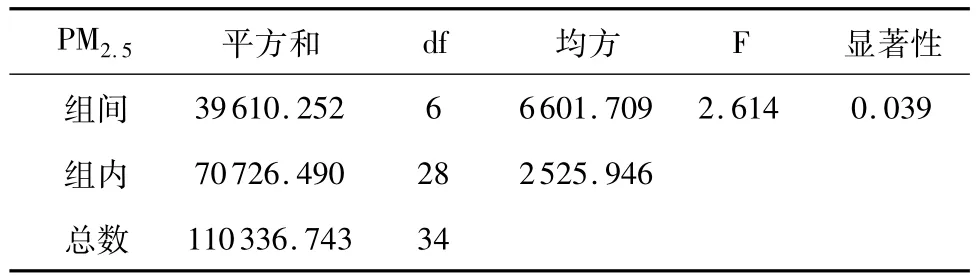
表7 方差分析(单因素方差分析)

表8 夜间风向情况对PM2.5浓度值变化的分析

表9 方差分析(单因素方差分析)

从表8、9中P=0.923＞α=0.05，可以看出白天风向情况对PM2.5浓度值变化没有显著性差异。

3 模型的建立

3.1 PM2.5回归分析的模型建立

为了综合考虑天气、温度、风力风向对PM2.5浓度值变化的影响，及综合相关分析和方差分析结果，建立(OLS)回归模型:

式中:Dij、Tij、Wij分别为上述虚拟变量选定设置。

3.2 模型的检验与结果分析

将搜集到的数据带入回归模型，由SPSS软件得到计算结果如表10所示。

表10 回归模型系数计算与检验

表10中B代表各自变量的系数，SPSS自动排出变量天气白天晴、多云，天气夜间晴，白天东风及夜间东风。而变量天气白天阴、雨、雪，天气夜间多云，气温最高，白天北风、东北风、南风、西南风、西北风、最大风力，夜间东南风、南、西南风、北风其系数的置信区间都过零点，可以看出这些变量与上文相关分析和方差分析结果一致的。

3.3 模型的改进［10］

用因子分析方法［9］分别对天气、温度、风向风力提取因子，带入回归模型中，得到改进模型:

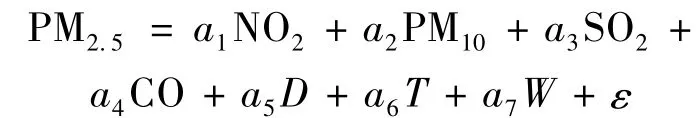
3.4 模型的改进的结果分析与检验

改进的回归模型系数计算与检验结果见11。改进的回归模型的回归显著性检验见表12。

表11 改进的回归模型系数计算与检验

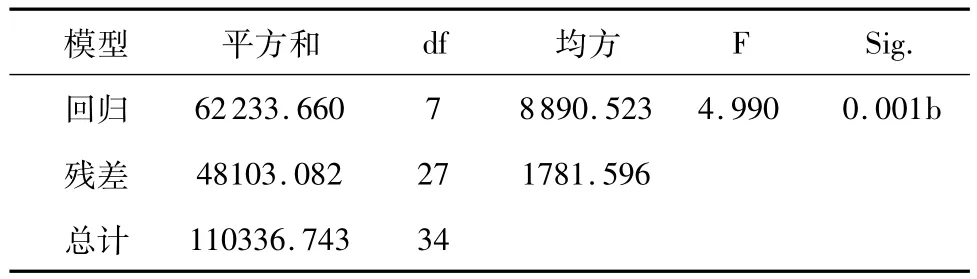
表12 改进的回归模型的回归显著性检验

表11模型检验的R平方值为87.5%，说明模型拟合程度较好。表12的F检验通过，说明回归模型显著，且P值=0.001＜0.1。对于残差的自相关检验D－W值为2.099，说明残差之间没有相关性。

3.5 PM2.5浓度值的预测

将近期2014年4月搜集到的各因素浓度及天气、温度、风力风向数据进行预测，其PM2.5浓度实际值与预测值关系见图1。

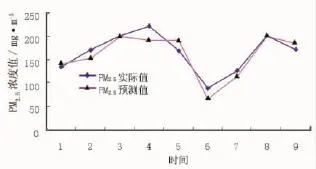
图1 PM2.5浓度实际值与预测值

从图1中可以看出，观测值与预测值很接近，说明预测效果较好。

4 结语

通过加虚拟变量的方法综合考虑天气、温度、风力风向的因素对PM2.5浓度值变化的影响。起初得到的回归模型检验性质较差，随后用因子分析方法将模型进行改进，得到天气因子、温度因子、风力风向因子，将因子、SO2、NO2、可吸入颗粒物(PM10)、CO的浓度与PM2.5浓度值进行拟合，得到拟合效果较好的回归函数，即PM2.5浓度值可由温度成份、风向风力、天气成份以及SO2、NO2、PM10、CO的浓度等七个变量解释的程度达到87.5%。将近期PM2.5浓度观测值与预测值相比较，发现数值很接近，说明预测效果较好。

［1］Appel B R，Tokiwa JH，Hsu J，et al.Visibility as related to atmospheric aerosol constituents［J］.Atmospheric Environment，1985，19 (9):1525－1534.

［2］Senaratne I.Elemental composition in source identification of brown haze in Auckland，New Zealand［J］.Atmospheric Environment，2004，38(19):3049－3059.

［3］Sisler JF，Malm W C.The relative importance of soluble aerosols to spatial and seasonal trends of impaired visibility in the United States［J］.Atmospheric Environment，1994，28(5):851－862.

［4］Chen LW A，Chow JC，Doddridge BQ et al.Analysis of a summertime PM2.5and haze episode in themid－Atlantic region［J］.Jounal of Air＆Waste Manage Association，2003，(53):946－956.

［5］Watson JG.Visibility:Science and regulation［J］.Journal of the Air＆Waste Management Association，2002，52(6):628－713.

［6］Schichtel B A，Husar R B，Falke SR，et al.Haze trends over the U-nited States，1980－1995［J］.Atmospheric Environment，2001，35 (30):5205－5210.

［7］Muraleedharan T R，Radojevic M，Waugh A，et al.Chemical characterization of the haze in Brunei Darussalam during the 1998 episode［J］.Atmospheric Environment，2000，34(17):2725－2731.

［8］杨龙，贺克斌，张强，等.北京秋冬季近地层PM2.5质量浓度垂直分布特征［J］.环境科学研究，2005(18):23－28.

［9］张涛.计量经济学精要［M］.北京:机械工业出版社2009.

［10］林海明.因子分析模型的改进与应用［J］.数理统计与管理.2009(6):135－168

Comprehensive prediction about PM2.5concentrations in the atmosphere

In view of the harm to hamen body PM2.5，in order to predict the PM2.5density and reduce its concentration throough the methods，com prehensive prediction research of PM2.5concentrations are carried out.The research through to the Xian a collection to the observation data analysis of air quality monitoring sites and PM2.5concentrations related factors，and then considering the weather，tem perature，w ind direction on the concentrations o f PM2.5observed value，by adding virtual variable and the method of factor analysis to extract factor，the related factors，the extraction of the weather，temperature，w ind direction factor and PM2.5observed concentration value regression prediction，finally get good prediction effect.

PM2.5;virtual variables;factor analysis;multip le regression

X701.2

:B

:1674－8069(2015)02－001－04

2014-12-20;

:2015-01-12

谢心庆(1988-)，女，回族，河南商丘人，在读研究生，研究方向为统计学。E－mail:celebration.1988@163.com

国家社科基金“新疆地区冰雹灾害预测研究”(14BTJ021)