配方法在初中数学解题中的应用

任秀娟

（陕西师范大学成州中学）

所谓配方，就是把一个解析式利用恒等变形的方法，把其中的某些项配成一个或几个多项式正整数次幂的和的形式。通过配方解决数学问题的方法叫配方法。其中，用得最多的是配成完全平方式：a2±2ab+b2=（a±b）2。配方法是数学中一种重要的恒等变形的方法，它的应用非常广泛，在分解因式、求二次函数的最值、化简求值、判定几何图形的形状、证明等式、比较大小、推导一元二次方程的求根公式等方面都经常用到它，下面我来例谈“配方法”在初中数学解题中的应用。

一、应用于分解因式

例1.分解因式x4＋4

解：原式=x4＋4x2＋4-4x2＝（x2＋2）2-（2x）2=（x2＋2x＋2）（x2-2x＋2）

例2.分解因式a2-4ab＋3b2-2bc-c2

解：原式=（a2-4ab＋4b2）-（b2+2bc＋c2）＝（a-2b）2-（b＋c）2＝（a-b＋c）（a-3b-c）

二、应用于求二次函数的最值

例3.已知x 是实数，求y＝x2-4x+5 的最小值。

解：由配方得y＝x2-4x＋4-4＋5=（x-2）2＋1

∵x 是实数，∴（x-2）2≥0，当x-2=0

即当x=2 时，y 最小，y最小=1

三、应用于化简求值

分析：本题若把x，y 直接代入，较为复杂，但用配方法将代数式适当变形，则可简化运算。

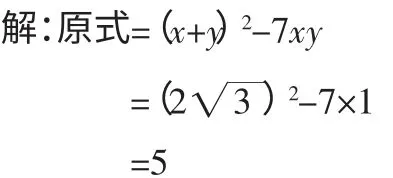
四、应用于判定几何图形的形状

例5. 已知：a、b、c 是△ABC 的三边，且满足a2＋b2＋c2-ab-bcca＝0，判定△ABC 是正三角形。

证明：由已知等式两边乘以2，得2a2＋2b2＋2c2-2ab-2bc-2ca=0，拆项、配方，得（a2-2ab＋b2）＋（b2-2bc＋c2）＋（c2-2ca＋a2）＝0，

（a-b）2＋（b-c）2+（c-a）2＝0.由实数的非负性，得：

a-b=0，b-c=0，c-a=0，∴a＝b，b＝c，c＝a，a=b=c.

故△ABC 是等边三角形。

五、应用于证明等式

例6.已知：（p2+q2）s2-2q（p+r）s+q2+r2=0，求证：q2=pr。

分析：本题要将已知方程左边拆开重组，进行配方变形，然后由非负数性质，便可找出其中奥妙。

证明：∵（p2+q2）s2-2q（p+r）s+q2+r2=0

∴p2s2+q2s2-2qps-2qrs+q2+r2=0

∴（ps-q）2+（qs-r）2=0

由非负数的性质，得ps-q=0 且qs-r=0，∴ps=q，qs=r

∴q2=pr

六、应用于比较大小

例7.若代数式M=10a2+b2-7a+8，N=a2+b2+5a+1，则M-N 的值（B）

A.一定是负数 B.一定是正数

C.一定不是负数 D.一定不是正数

分析：本题通过作差法拆项、配成完全平方，使差大于零来比较大小。

解：（作差法）M-N=10a2+b2-7a+8-（a2+b2+5a+1）

=10a2+b2-7a+8-a2-b2-5a-1

=9a2-12a+7=9a2-12a+4+3=（3a-2）2+3＞0，故选B。

七、应用于推导一元二次方程的求根公式

公式法是由配方法解一元二次方程的一般形式得来的：

用配方法解关于x 的方程ax2+bx+c=0（a≠0），

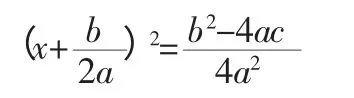
∵a≠0，∴a2≠0

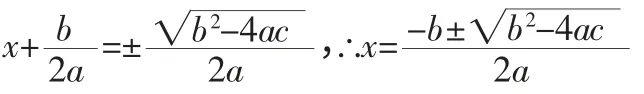
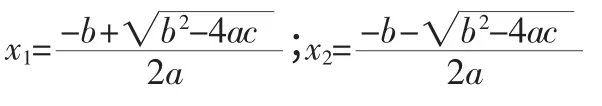
当b2-4ac＜0 时，此方程无实数根。

一元二次方程ax2+bx+c=0（a≠0），求根公式:

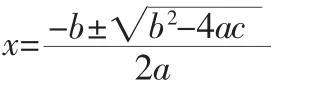
因为配方法在初中数学中占有非常重要的地位，是恒等变形的重要手段，是研究相等关系，讨论不等关系的常用技巧，是挖掘题目中隐含条件的有力工具，所以一定要让学生掌握这种方法。