基于多分类支持向量机和D-S证据理论的轴承故障诊断

梅检民，赵慧敏，肖云魁，周 斌

(1.军事交通学院汽车工程系，天津 300161; 2.天津大学机械工程学院，天津 300072)



2015021

基于多分类支持向量机和D-S证据理论的轴承故障诊断

梅检民1,2，赵慧敏1，肖云魁1，周 斌2

(1.军事交通学院汽车工程系，天津 300161; 2.天津大学机械工程学院，天津 300072)

针对支持向量机(SVM)硬判定输出分类结果缺乏定量评价的问题，提出了一种多分类SVM后验概率建模的改进方法。通过引入D-S证据理论，得到多分类SVM在D-S证据理论识别框架下的基本概率分配，使样本在分类时同时具有定性解释和定量评价。接着，将多源信息送入SVM之后在决策级对多个SVM分类输出进行证据融合，以提高诊断精度。最后，将该方法应用于轴承故障的诊断中。结果表明，该方法能正确分类采用单源信息时所错分样本，降低识别的整体误差，显著提高故障诊断的准确性。

故障诊断；支持向量机；后验概率；D-S证据理论；信息融合

前言

机械故障样本获取困难，限制了人工神经网络在机械故障模式分类中的应用。20世纪90年代初由Vapnik等人提出的支持向量机(support vector machine, SVM)能够在训练样本较少的情况下得到较强的分类推广能力，较好地解决了小样本、非线性和高维数等模式识别问题[1]。然而传统SVM不提供概率输出，在进行样本分类学习时，只考虑两种极端情况，即属于某一类的概率为1或0，因此SVM对故障模式识别的不确定性问题缺乏识别结果的准确性解释[2]。D-S证据理论引入了信任函数，满足比概率论弱的公理，并能区分不确定性的差异。D-S证据理论作为一种不确定性推理方法，利用多源冗余信息进行融合，可以有效提高推理准确度，在故障诊断领域受到越来越多的关注[3]。本文中提出多分类SVM后验概率输出建模方法，并将其与D-S证据理论相结合，对轴承故障进行融合诊断，提高诊断精度和准确率。

1 SVM后验概率输出建模

1.1 二分类SVM后验概率输出

Wahha和Platt最早在二分类SVM方法中引入后验概率，通过样本的后验概率来确定样本的类别，使样本在分类时不仅具有定性解释，而且具有定量评价。SVM的标准输出[4]为

(1)

支持向量到分类面之间的距离记为

dsvm=1/‖ω‖

(2)

则任意样本点x到分类面之间的距离为

dx=f(x)/‖ω‖

(3)

从SVM分类超平面的几何角度，可通过样本与最优分类面间距离的远近来定量评价分类问题中的样本属于所在类可能性的大小，即后验概率。由式(2)和式(3)得出f(x)=dx/dsvm，f(x)反映了样本x经非线性映射至高维隐空间的最优分类超平面的相对代数距离，反映了对类别的相对支持程度。

概率输出函数须满足两个条件：(1)函数的值域为[0,1]；(2)函数满足单调性。Platt提出将后验概率视为sigmoid函数，将SVM的输出fi(x)映射到[0,1]，后验概率输出形式[5]为

(4)

(5)

式中：i=1,2,…,l；yi为样本的类别标签。

1.2 多分类SVM后验概率输出

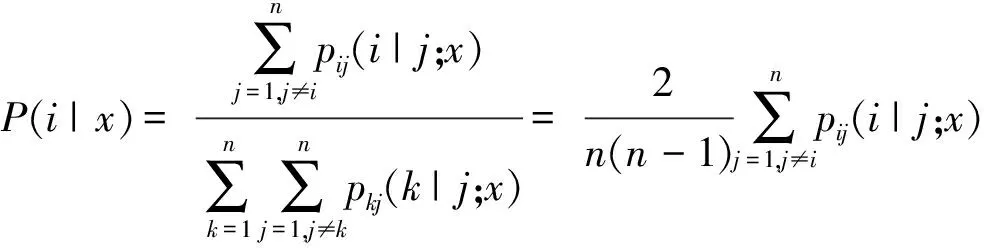
(6)

式中：pij(i|j;x)表示由第i类和第j类构成的两类分类器计算所得x属于第i类的后验概率。

(7)

简记pi=p(i|x)，p(i|j)=pij(i|j,x)，式(7)可以整理为

(8)

式中p(i|j)=1-p(j|i)，同时满足约束条件：

(9)

求解方程组，可以得到样本x在各类中的后验概率pi。式(6)和式(8)组合为一个超定方程组，其系数矩阵的列向量组线性无关，得到的最小二乘解是唯一的。

2 D-S证据理论基本原理

设Θ为识别框架，若集函数m：2θ→[0,1](2θ为Θ的幂集)满足

(1) 不可能事件的基本概率为0，即：m(φ)=0；

u(Θ)=Pls(A)-Bel(A)

(10)

[Bel(A),Pls(A)]称为置信区间，表示对A的不确定区间。

设Bel1和Bel2是基于同一识别框架Θ的两个置信度函数，m1和m2分别是对应的基本可信数，焦元分别为A1,A2,…,AK和B1,B2,…,BL，并假设

(11)

合成后的基本概率分配函数m：2θ→[0,1]则为

(12)

从式(12)可以看出，多个证据的合成与次序无关，多个证据的合成计算可以用两个证据合成的计算递推得到。

3 多分类SVM后验概率与证据理论的结合

3.1 后验概率的BPA输出

Platt给出的仿真结论表明：式(4)的概率输出模型并没有明显提高分类器的识别精度，而是与原SVM精度相近[8]。其原因在于sigmoid函数只是将SVM的输出映射到[0,1]，并没有真正反映样本的后验概率。因此SVM的后验概率输出更符合证据理论框架下的基本概率分配，首先将其转换为证据理论识别框架下的基本概率分配函数BPA。

定理：如果一组训练样本能够被一个最优分类面或广义最优分类面分开，则对于测试样本分类错误率期望的上界是训练样本中平均的支持向量占总训练样本数的比例[9]：

E(Perror)≤E(nsv)/(N2-1)

(13)

式中：N2表示训练样本的总数；E(nsv)表示支持向量个数的平均值。一个SVM分类器的上限正好反映了SVM对样本x的不确知性，即识别框架的u(Θ)。由此得到多分类SVM证据理论识别框架下的基本概率分配

mi(x)=pi(1-E(Perror))，i=1,2,…,M

(14)

mΘ=E(Perror)

(15)

3.2 融合决策

诊断决策层采用D-S证据理论推理方法，通过对同一识别框架上的各证据体进行融合推理，最终形成决策结果。作用到框架上的证据体由特征诊断层输出结果组成。采用如下方法进行判定：如果x点满足m+(x)>m-(x)，m+(x)-m-(x)>ε1，m(Θ)<ε2，则把x判为正类，反之为负类。其中ε1的选取参照Platt基于SVM概率输出判定的做法，取ε1=0；ε2的选取考虑无法分类时的极限情况：当f(x)=-B/A时，SVM无法做出判定，此时m+(x)=m-(x)=1/2(1-E(Perror))，多个SVM局部决策进行融合时，取多个SVM的最小值ε2=min{(1-ESVM1(Perror))/2,(1-ESVM2(Perror))/2,…,(1-ESVMN3(Perror))/2}，其中N3为SVM的个数。

4 基于多分类SVM后验概率和D-S证据理论的轴承故障诊断

采用上述方法对轴承故障进行诊断，对象为发动机第3缸前后两道曲轴轴承和第3缸连杆轴承。曲轴轴承配合间隙分别设置为0.08mm(正常)、0.20mm(轻微磨损)、0.40mm(严重磨损)，连杆轴承间隙设置为0.07mm(正常)、0.1mm(轻微磨损)、0.2mm(严重磨损)，对应曲轴轴承和连杆轴承皆正常、曲轴轴承轻微异响、曲轴轴承严重异响、连杆轴承轻微异响、连杆轴承严重异响5种工作状态。振动传感器分别放置在第3缸顶部、缸体右侧、油底与缸体结合处右侧，如图1所示。

经反复试验确定发动机转速为1 300r/min时故障特征最明显，采集该转速下不同位置传感器的振动信号。对各通道信号分别进行4层db2小波包分解，再对分解后各频段的时域序列重构信号进行AR谱分析。为便于数据分析，将分解重构后柴油机加速振动信号的频率归一化，分为16段，各频段所代表的实际频率如表1所示。选取训练样本和测试样本各10组，每种技术状态对应两个样本，如表2和表3所示。表中，A-E4,1、A-E4,2、A-E4,3、B-E4,1、B-E4,2、B-E4,3、C-E4,1、C-E4,2、C-E4,3分别表示A、B、C 3处加速振动信号进行小波包AR谱分析后的2、3、4频段能量。

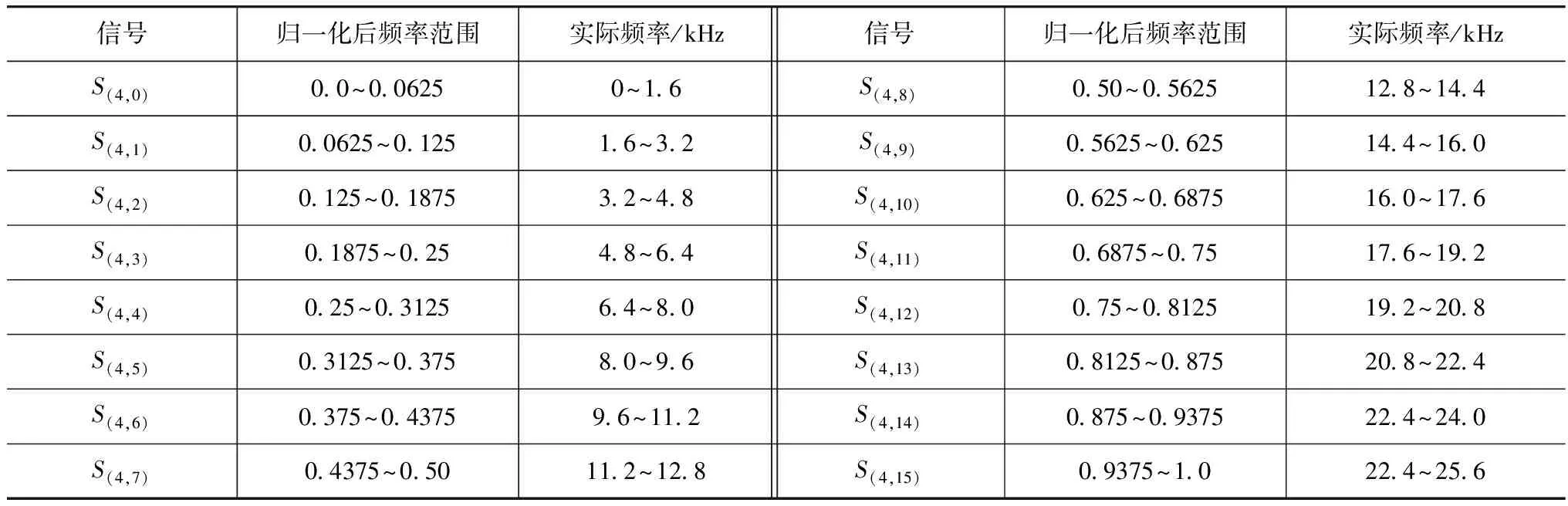
表1 16个频率分段代表的实际频率范围

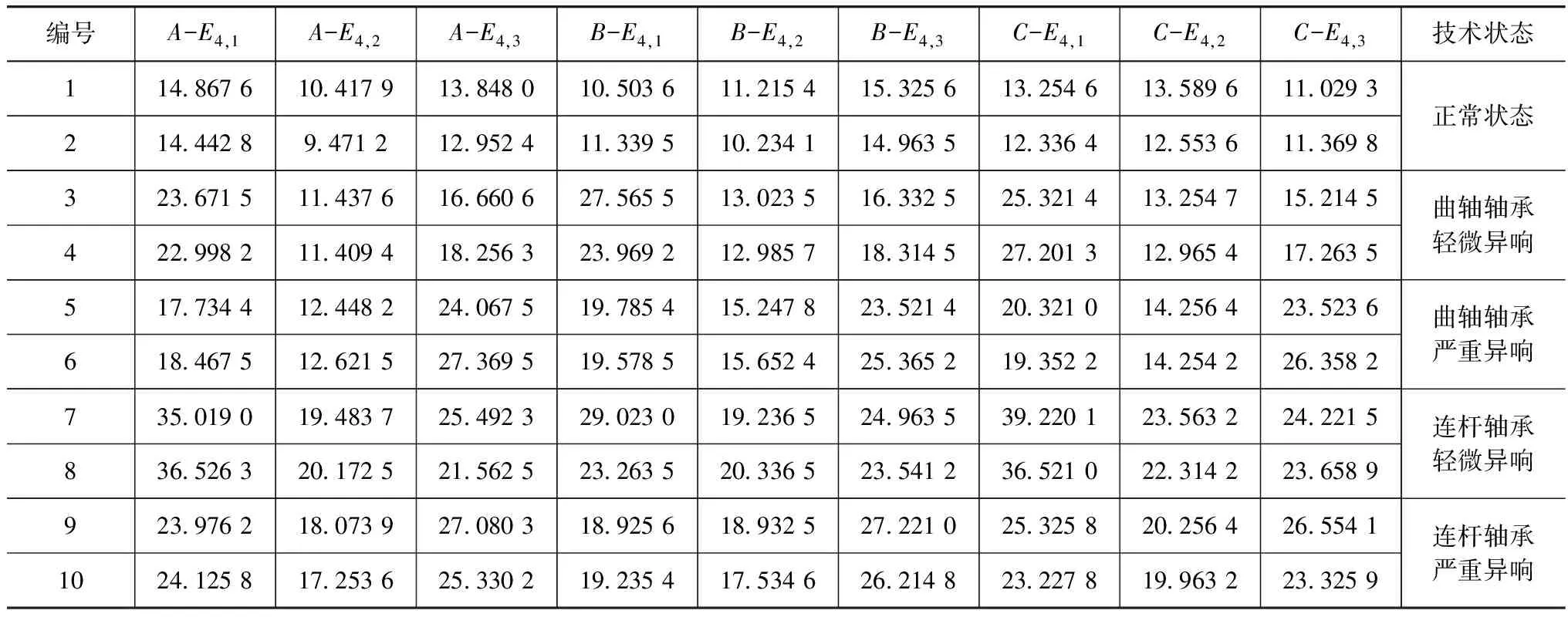
表2 SVM模型训练样本

表3 SVM模型检验样本

用表2样本中不同传感器的数据分别进行训练，得到3个SVM分类器，将表3样本输入3个不同的分类器，并采用式(6)～式(9)算法求得各个SVM的后验概率输出，如表4所示。

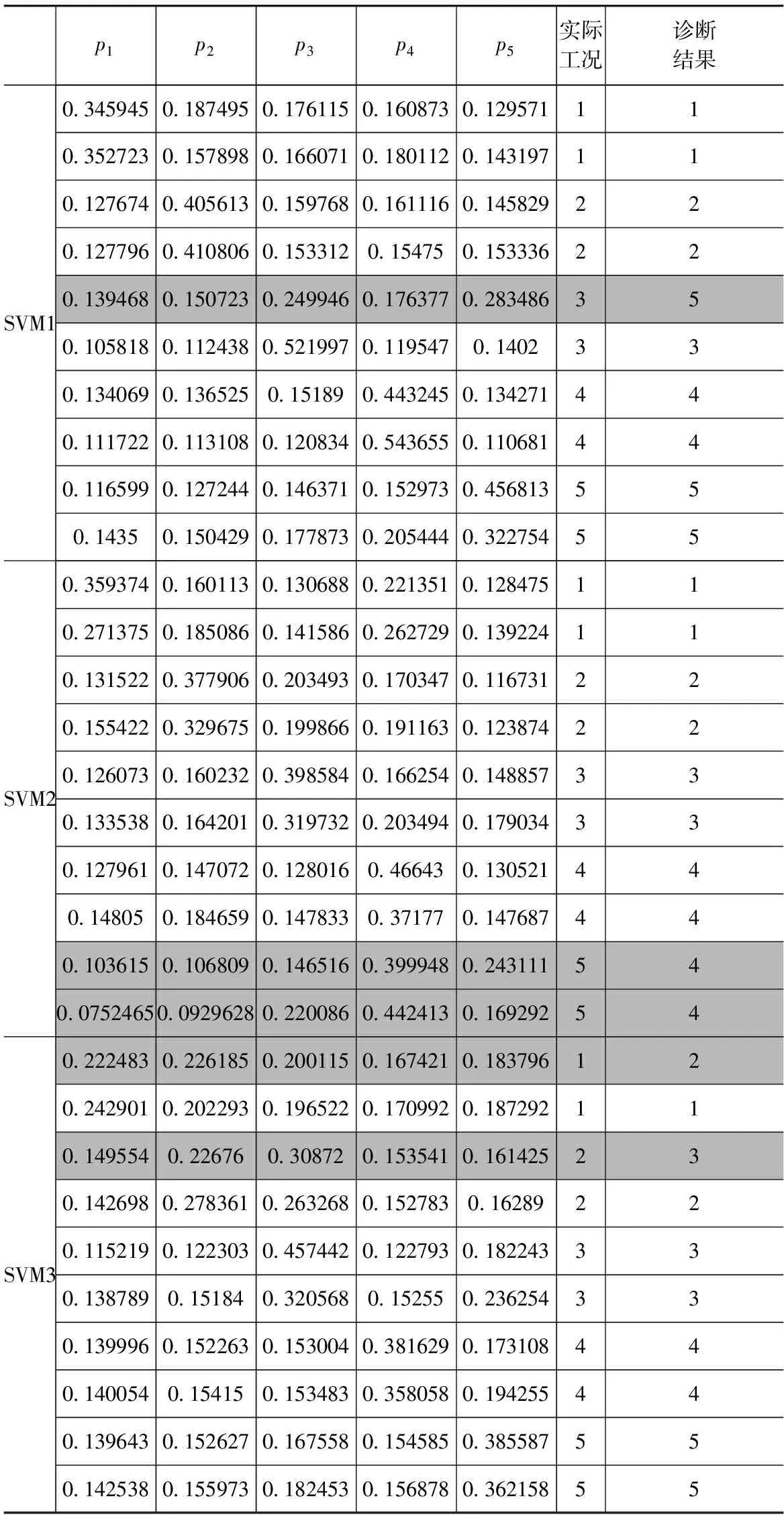
表4 测试样本的SVM后验概率输出

由表4阴影部分可知，有5个样本被错分。为提高识别精度，将3个SVM的输出结果进行D-S融合。首先按式(13)～式(15)得到错分样本的BPA，如表5所示。接着按照式(12)算法融合，得到融合诊断结果如表6所示。

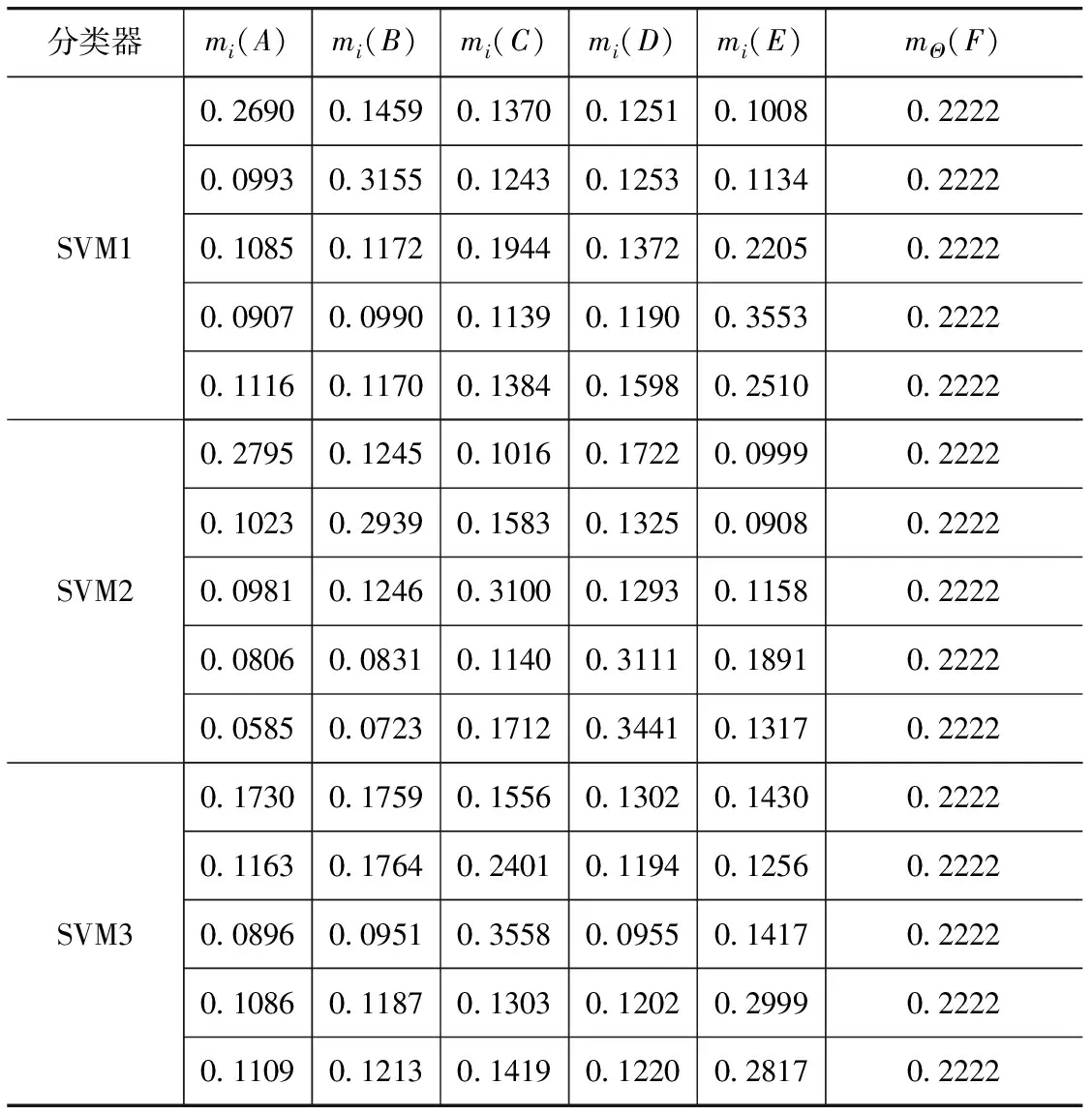
表5 错分的测试样本证据体的基本概率分配

表6 错分测试样本的证据合成

从表4、表5和表6可以看出，证据融合后的诊断结果准确度达到了100%，对SVM局部诊断决策错分的样本也能正确识别，诊断精度大大提高。与此同时，从表5与表6的比较可以看出，经过证据融合后置信区间范围和证据的不确定性mΘ明显减小，说明经融合后，诊断结果的不确定性减小，诊断精度大幅提高，证明多分类SVM后验概率与D-S证据理论相结合的故障诊断模型的有效性和准确性。

5 结论

(1) 改进的多分类SVM后验概率输出模型将被测样本属于各二分类SVM的概率作为权值，符合多类样本的实际分布，提高了SVM后验概率的准确性。

(2) 将SVM误差上界分配给识别框架，符合D-S证据理论的不确知性质，提高了算法的有效性。采用SVM和D-S证据理论的集成故障诊断模型，能够显著提高轴承故障诊断的精确性。

[1] 李凌均,张周锁,何正嘉.支持向量机在机械故障诊断中的应用研究[J].计算机工程与应用,2002,19:19-21.

[2] 杜京义,侯媛彬.基于最小风险的SVM及其在故障诊断中的应用[J].振动、测试与诊断,2006,26(2):108-159.

[3] 闫宏莉.证据理论在机械设备故障诊断中的应用研究[D].北京:华北电力大学,2006.

[4] Vapnik.统计学习理论[M].许建华,张学工,译.北京:电子工业出版社,2004.

[5] Platt John C. Probabilistic Output for Support Vector Machine and Comparisons to Regularized Likelihood Methods[M]. Advances in Large Margin Classifier, Cambridge: MIT Press,2000.

[6] Wu Ting-Fan, Lin Chih-Jen, Weng Ruby C. Probability Estimates for Multi-class Classification by Pairwise Coupling[J]. Journal of Machine Learning Research,2004(5):975-1005.

[7] Dempster A P. Upper and Lower Probabilities Induced by a Multivalued Mapping[J]. Annals of Mathematical Statistics.1967,38:325-339.

[8] Tipping Michael E. Sparse Bayesian Learning and the Relevance Vector Machine[J]. Journal of Machine Learning Research,2001(1):211-244.

[9] 边肇祺,张学工,等.模式识别[M].北京:清华大学出版社,2000.

Fault Diagnosis of Bearings Based on Multi-class SVM and D-S Evidence Theory

Mei Jianmin1,2, Zhao Huimin1, Xiao Yunkui1& Zhou Bin2

1.DepartmentofAutomobileEngineering,MilitaryTransportationUniversity,Tianjin300161;2.SchoolofMechanicalEngineering,TianjinUniversity,Tianjin300072

In view of the problem that the classification results of hard decision output of support vector machine (SVM) lack of quantitative evaluation, an improved modeling method for the posterior probability of multi-class SVM is proposed. Through the introduction of D-S evidence theory, the basic probability assignment (BPA) of multi-class SVM under the recognition frame of evidence theory is obtained to enable the samples have both qualitative explanation and quantitative evaluation. And then the multi-source information is delivered to SVM to conduct the evidence fusion of several SVM classification outputs for improving diagnostic accuracy. Finally the method is applied to the fault diagnosis of bearings with a result showing that the method proposed can correctly classify the samples being classified wrongly using single-source information, reduce the overall error of recognition frame, and enhance the correctness of fault diagnosis remarkably.

fault diagnosis; SVM; posterior probability; D-S evidence theory; information fusion

原稿收到日期为2012年8月17日，修改稿收到日期为2013年8月8日。