基于响应面法的汽车转向系统可靠性优化*

路怀华,于德介,吕 辉

(湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082)



2015019

基于响应面法的汽车转向系统可靠性优化*

路怀华,于德介,吕 辉

(湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082)

针对结构参数的不确定性会导致确定性优化结果不可靠的问题，提出一种将可靠性分析与优化技术相结合的转向系统可靠性优化方法。该方法基于响应面方法构建转向系统优化近似模型，以1阶固有频率为约束，总质量为优化目标对转向系统进行可靠性优化。结果表明，采用该方法对汽车转向系统进行优化，减小了系统质量，提高系统的1阶固有频率，避免怠速共振，达到可靠性优化的目的。

汽车转向系统；固有频率；响应面；可靠性优化

前言

汽车转向系统的振动特性优化对提高汽车NVH特性具有重要意义。文献[1]中采用有限元法研究了仪表板和转向系统的NVH特性对板件厚度的灵敏性，为仪表板和转向系统设计提供指导；文献[2]中在建立汽车悬架和转向系统力学模型的基础上，采用模拟退火优化算法对转向系统进行优化，提高了汽车的操纵稳定性；文献[3]中在转向系统有限元模型的基础上，利用响应面法对转向系统固有频率进行了优化，改善了汽车NVH特性。

传统的优化设计忽略了转向系统结构参数的不确定性，得到的最优解只是数学意义上的最优解，且总是接近各个约束的边界。实际上，工程问题中的各类参数，如材料参数、几何尺寸参数、载荷和边界条件等通常是不确定的，参数的波动往往会导致确定性优化得到的最优解不满足约束条件，从而使最终的设计结果不可靠，甚至不可行[4]。因此，在确定性优化设计的基础上开展可靠性优化设计具有重要的现实意义。

可靠性优化设计方法弥补了确定性优化设计的不足，既能定量给出可靠度指标，又能得到问题的优化解，是一种更具工程应用前景的优化设计方法[5-6]。文献[7]中将可靠性理论引入到飞机机翼的优化设计中，结合空气动力学、结构动力学和优化算法建立了飞机机翼的可靠性优化模型，优化结果在满足飞机机翼力学性能可靠性约束条件下使得结构质量最小。文献[8]中将可靠性分析与优化技术相结合，提出一种改善汽车前轴动态特性的可靠性优化设计方法，有效改善了前轴的动态特性。

为避免转向系统怠速共振，其1阶模态频率应超过发动机工作转速范围内的主要激励力的激励频率。本文中在结构模态分析、响应面法、可靠性理论和优化算法的基础上，提出一种汽车转向系统的可靠性优化方法。该方法以降低转向系统总质量为优化目标，选取转向系统结构1阶模态频率为约束条件，并通过灵敏度分析确定设计变量，再基于响应面法构建结构可靠性优化近似模型。对某汽车转向系统结构的可靠性优化结果表明，获得的可靠最优解有效降低了结构质量，避免了怠速共振，达到了可靠性优化的目的。

1 可靠性优化原理

1.1 可靠性指标

可靠性指标是评价系统或产品可靠性的量化指标，常用评定可靠性的指标有可靠度、累积失效概率、失效率、平均寿命和可靠寿命等。可靠度是可靠性的量化指标，若可靠度不满足设计要求，则须进行可靠性优化设计，故可靠度优化设计是以可靠性分析为基础的。结构可靠性定义为满足约束条件的概率，可靠度的计算公式为

(1)

式中：fX(X)为随机参数向量X=(X1,X2,…,Xn)的联合概率密度函数；g(X)为约束函数，表示结构的两种状态

(2)

其中，g(X)称为极限状态方程，表示结构处于临界状态或极限状态。

可靠性指标β定义为

β=μg/σg

(3)

式中：μg为约束函数g(X)的均值；σg为约束函数g(X)的标准差。

采用1阶可靠性分析方法计算可靠性指标参数中约束函数的均值和标准差分别为

(4)

式中μX为随机参数向量X的均值。

在随机参数向量X服从正态分布时，可以用失效点处状态表面的切平面近似模拟极限状态表面，获得可靠度的1阶估计

R=Φ(β)

(5)

式中Φ(·)表示标准正态分布函数。

1.2 可靠性优化的数学模型

可靠性设计将设计变量(如载荷、应力、强度和板件厚度等)视为服从某种分布规律的随机变量，用概率统计方法设计出符合产品可靠性指标要求的主要参数[9]。可靠性优化的数学模型可表示为

(6)

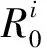
2 转向系统可靠性优化

汽车转向系统结构的第1阶模态频率是衡量该结构在低频共振时抵抗变形的能力，如果1阶模态频率值过低，接近发动机怠速工况激励频率，则容易引起共振。转向系统的怠速振动主要是由发动机怠速工况下的2阶往复惯性力激励产生，其频率与发动机的气缸数和怠速转速有关。四缸发动机的激振频率一般为20～35Hz。为避免转向盘怠速共振，则要求转向系统固有频率高于发动机的怠速激振频率。因此应使转向系统结构优化后的第1阶模态频率不低于给定值。考虑汽车轻量化的要求，本文中选取转向系统总质量为可靠性优化的目标。根据设计要求和工艺、强度的限制，确定设计变量的尺寸约束，进而建立汽车转向系统的可靠性优化模型。

在进行汽车转向系统振动性能可靠性优化时，须多次调用有限元分析程序。为减少计算工作量，本文中先用灵敏度分析确定系统优化的设计变量，再用响应面模型代替复杂的、具有大量自由度的结构仿真模型。

基于响应面法的结构振动性能可靠性优化方法首先确定目标函数和约束函数；然后通过试验设计方法选定试验设计点，用有限元法计算试验设计点上的目标函数和约束函数，根据试验设计点及其对应的目标函数值和约束函数值进行响应面拟合，建立目标函数和约束函数值关于设计变量的响应面模型；最后进行结构振动特性可靠性优化。

用最小二乘法原理拟合得到响应面模型[10]，本文中采用如下二次多项式响应面模型[11]：

(7)

基于响应面法的汽车转向系统振动特性可靠性优化流程如图1所示。

3 数值算例

3.1 汽车转向系统模态分析

以国内某微型车的转向系统为研究对象进行可靠性优化。该转向系统由转向柱、转向臂、转向盘和各种安装支架等组成。材料为钢及其合金材料。为减少计算量，同时能较真实地模拟转向系统的振动特性，本文中采用有限元软件Altair Hypermesh建立如图2所示的转向系统有限元模型，其中结构模型单元总数为11 215，节点总数为11 761，结构边界采用固定约束。

转向系统是汽车中的重要总成，它接受来自发动机的激励，转向系统模态分析的目的是确定其固有频率和振型等模态参数，考查其固有频率是否与发动机激励频率接近，以避免发生共振。从安装状态下的转向系统有限元模型计算得到的结构前4阶固有频率值和振型如表1所示，图3为转向系统第1阶振型图。

表1 转向系统模态

由以上分析可以看出：转向系统的1阶固有频率为34Hz，与发动机的怠速频率比较接近，有可能发生共振。因此有必要对转向系统结构进行优化。

3.2 灵敏度分析

为提高优化效率，本文中以转向系统板件的厚度为设计变量，计算1阶固有频率对板件厚度的灵敏度值，从计算结果可知，只有转向柱安装支架、转向柱、转向轴固定支架、转向盘和转向轴5个主要板件厚度的灵敏度绝对值大于1，因此，选择上述5个板件的有限元壳单元的板厚作为设计变量，见表2。分别用参数t1、t2、t3、t4和t5表示这5个变量，见图3，其初始值分别为1.8、1.8、2.5、1.5和5.0mm。

表2 转向系统5个板件厚度的灵敏度值

3.3 建立响应面模型

为提高计算效率，本文中以转向系统结构的1阶固有频率为约束函数，采用拉丁超立方试验设计在整个设计空间进行采样，获得60个样本点，然后通过有限元计算，获得结构1阶固有频率值的仿真数据。根据数值仿真结果，采用最小二乘法计算回归系数矩阵，构造约束函数的二次多项式响应面拟合模型。具体表达式如下：

ω=24.23+6.99t1+1.54t2+6.531t3-18.68t4+2.05t5+

0.55t1t2+0.54t1t3-1.28t1t4+0.34t1t5+0.78t2t3-

0.699t2t4+0.17t2t5-0.98t3t4+0.39t3t5-0.008t4t5-

(8)

式中ω为汽车转向系统的1阶固有频率。

对响应面模型进行误差分析，得知模型的不可靠概率不超过1%，能够比较准确地反映目标函数和设计变量的统计规律性。同时，与设计变量直接相关的转向系统总质量M可表示为M=13.04+0.94t1+1.6575t2+0.171t3+1.823t4+0.378t5

(9)

3.4 可靠性优化

以降低汽车转向系统总质量为优化目标，以该结构的1阶模态固有频率(不低于怠速激振频率)为约束，对该转向系统进行优化。结构振动性能的确定性优化数学模型为

(10)

汽车转向系统结构振动特性的确定性优化结果见表3，为了分析其可靠度，对约束函数进行可靠性分析。根据工程经验，假定各个变量服从正态分布，各个变量以确定性优化解为均值，取均方差与均值之比为0.05，采用蒙特卡洛方法计算，确定性优化结果的1阶固有频率约束可靠度只有50%，使确定性优化的固有频率值处于临界状态，一旦加工制造等因素使设计变量产生轻微波动，就可能使其结果超出约束范围，导致怠速共振。因此须在确定性优化的基础上进行可靠性优化。

可靠性优化是给定各个设计变量的概率分布函数，将确定性设计约束转化为概率约束，假定各个设计变量服从正态分布，以确定性优化解为均值，取均方差与均值之比为0.05，采用基于响应面法的可靠性优化算法进行转向系统结构振动特性可靠性优化。可靠性优化数学模型为

(11)

式中：g(t,X)为式(10)中的约束函数，即1阶固有频率值ω≥37；R0为目标可靠度，取为0.95。

可靠性优化后的设计变量和性能参数(转向系统结构质量、1阶固有频率及其约束可靠度值)也列于表3中。从表3可知，可靠性优化后汽车转向系统的1阶固有频率从34Hz提高到38.5Hz，且设计约束达到95%的可靠度，满足了可靠性设计的要求，同时结构质量也有所下降。

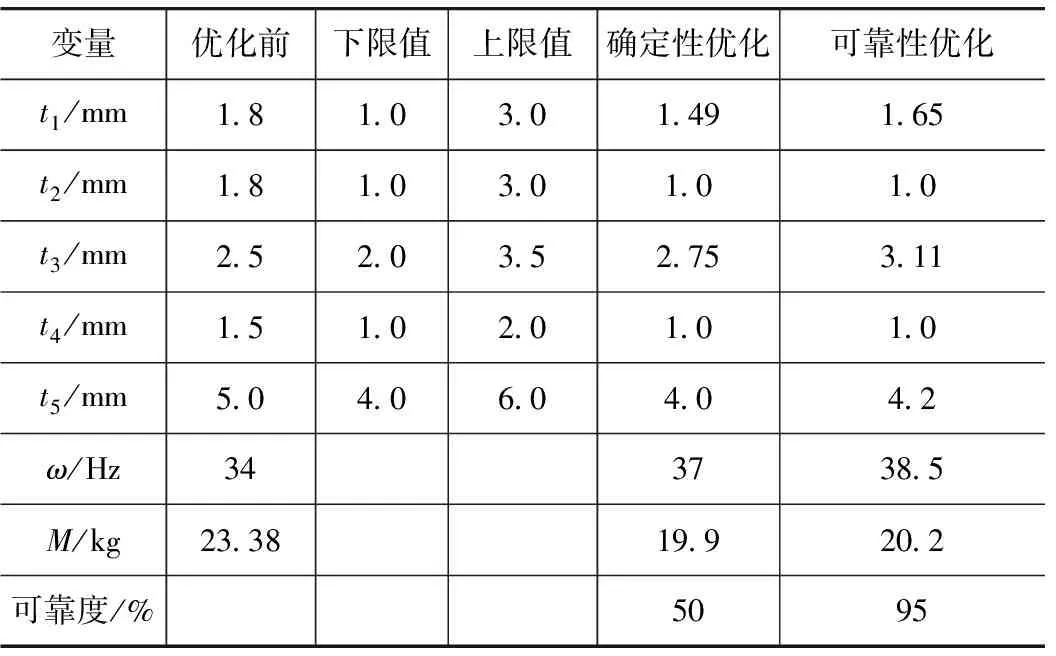
表3 汽车转向系统结构优化前后结果

可靠性优化后结构的1阶模态振型如图4所示。综上所述，可靠性优化后的转向系统在满足设计约束条件下，降低了系统结构质量，提高了约束设计的可靠度，有效避免了发动机怠速共振的产生，达到了可靠性优化的目的。

4 结论

(1) 可靠性是评价产品设计质量的重要指标，可靠性优化方法在设计阶段就考虑了各种不确定因素的影响，因而在获得最优解的同时，能够较大幅度地提高产品的可靠性。

(2) 将可靠性分析与优化技术相结合，基于响应面法和灵敏度分析对转向系统结构振动特性进行可靠性优化。在优化过程中，运用灵敏度分析避免了选择设计变量的盲目性，采用响应面法构造约束函数的拟合模型，简化了优化计算的工作量，提高了计算效率。

(3) 某微型车转向系统结构的可靠性优化结果表明：本文的方法考虑了设计参数的不确定性，有效降低了结构质量，避免了怠速共振，达到了可靠性优化设计的目的。

[1] Lam K P, Behdinan K, Cleghom W L. A Material and Gauge Thickness Sensitivity Analysis on the NVH and Crashworthiness of Automotive Instrument Panel Support[J]. Thin-walled Structure,2003,41:1005-1018.

[2] 王其东,姜武华,陈无畏,等.主动悬架和电动助力转向系统机械与控制参数集成优化[J].机械工程学报,2008,44(8):68-73.

[3] 周萍,于德介,臧先国,等.采用响应面法的汽车转向系统固有频率优化[J].汽车工程,2010,32(10):883-887.

[4] Valdebenito M A, Schuёller G I. Efficient Strategies for Reliability-based Optimization Involving Nonlinear Dynamical Structures[J]. Computers and Structures,2011,89:1797-1811.

[5] Wu Y T. Computational Methods for Efficient Structural Reliability and Reliability Sensitivity Analysis[J]. AIAA,1994,32(8):1717-1723.

[6] Enevoldsen I, Sorensen J D. Reliability-based Optimization in Structural Engineering[J]. Structural Safety,1994,15(3):169-196.

[7] Yu X Q, Du X P. Reliability-based Multidisciplinary Optimization for Aircraft Wing Design[J]. Structure and Infrastructure Engineering,2006,2(3-4):277-289.

[8] 臧献国,于德介,姚凌云.汽车前轴动态特性的可靠性优化设计[J].中国机械工程,2011,22(1):102-105.

[9] Youn B D, Choi K K. An Investigation of Nonlinearity of Reliability-based Design Optimization Approaches[J]. Journal of Mechanical Design,2004,126(4):403-411.

[10] Liang X H, Lin Z Q, Zhu P. Acoustic Analysis of Damping Structure with Response Surface Method[J]. Applied Acoustics,2007,68:1036-1053.

[11] Khayet M, Cojocaru C, Essalhi M. Artificial Neural Network Modeling and Response Surface Methodology of Desalination by Reverse Osmosis[J]. Journal of Membrane Science,2011,368:202-214.

Reliability Optimization of Vehicle Steering SystemBased on Response Surface Method

Lu Huaihua, Yu Dejie & Lü Hui

HunanUniversity,StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,Changsha410082

Aiming at the problem that the uncertainty of structural parameters could lead to unreliable results of deterministic optimization, a reliability optimization method for vehicle steering system is proposed based on the combination of reliability analysis and optimization technology. With a surrogate model built by response surface method, and taking the first order natural frequency as constraint with minimizing system mass as objective, a reliability optimization of steering system is conducted. The results show that the optimization of steering system with the method proposed reduces the mass of system, increases the first order natural frequency and avoids the resonance at idling speed, achieving the objective of reliability optimization.

vehicle steering system; natural frequency; response surface; reliability optimization

*湖南大学汽车车身先进设计制造国家重点实验室自主课题(71375004)和湖南省研究生科研创新项目(CX2013B143)资助。

原稿收到日期为2012年11月23日，修改稿收到日期为2013年6月5日。