抽油杆经济使用年限的可靠性分析*

李 其 李秀伟 葛修梅

（东北石油大学机械科学与工程学院） （大庆油田第一采油厂）

0 引言

抽油机井杆柱最主要的失效形式是疲劳断裂[1]。抽油杆柱的实际循环应力幅值和抽油杆实际疲劳强度极限常常影响抽油杆柱的疲劳寿命。抽油杆的使用时间越长，表面的划痕和腐蚀斑坑也会越严重，实际的疲劳强度与以前相比也会变低，致使抽油杆柱的可靠性也越来越低。当抽油杆柱的可靠度下降到一定程度时，需要将其报废。因此，我们在研究抽油杆柱疲劳寿命可靠性预测方法的基础上，建立了抽油杆经济使用年限的可靠性评价方法。

1 抽油杆柱应力循环特性的仿真模型

1.1 抽油杆柱轴向振动仿真模型

载荷是零部件疲劳强度计算的基础，是进行疲劳寿命可靠性预测的前提。应用波动方程理论描述抽油杆柱的轴向振动，其波动方程为[2]：

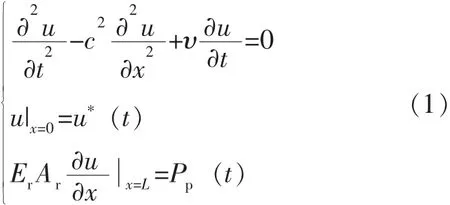
式中u——截面x在任意时刻t的位移，m;

c——声音速度，m/s;

Er——弹性模量，Pa;

υ——阻尼系数，1/s;

u*（t） ——位移，m;

Ar——横截面积，m2;

L——泵深，m;

Pp——抽油泵柱塞液柱负荷，N。

1.2 抽油杆柱轴向载荷仿真模型

用牛顿差分法求波动方程，单级杆柱任意截面的位移计算公式为[3]：

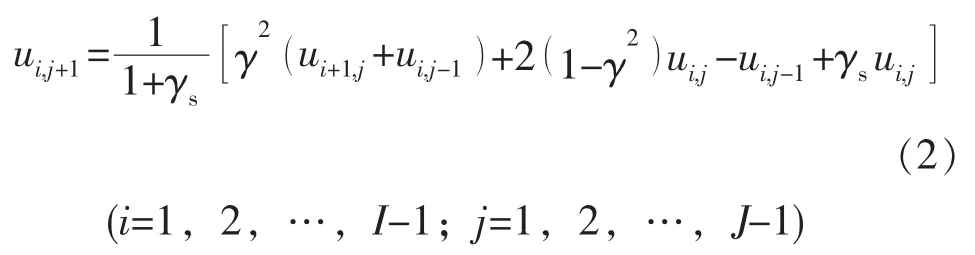
其中

式中ui,j——节点i在时间离散点j的位移，m;

Δt——时间步长，s;

Δx——轴向离散的单元长度，m;

I——轴向离散的单元数;

J——离散的区间数。

对于多级组合的杆柱，相邻杆连接节点的波动方程的差分形式为：

其中

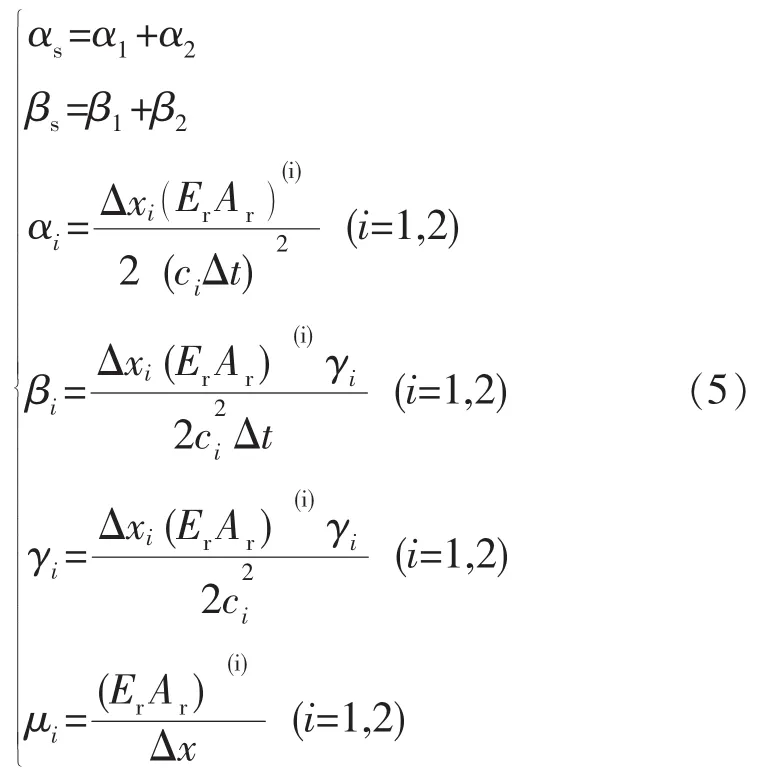
抽油杆柱轴向节点在时间离散点的轴向载荷，即在位置为x和时间为t时轴向载荷的计算公式为：

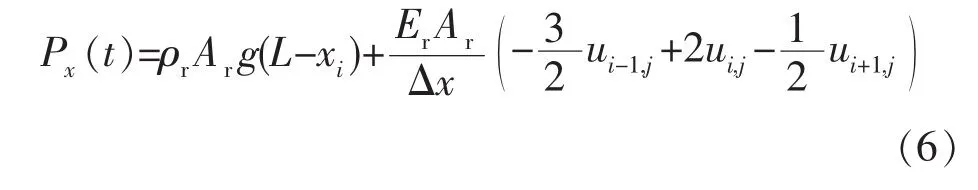
1.3 循环应力的计算模型

抽油杆柱是由抽油杆、螺纹连接而成的，其中螺纹的连接包括接头和接箍。对于抽油杆柱螺纹的连接段，不考虑螺纹连接部分轴向尺寸，只考虑螺纹连接预紧力的影响。抽油杆柱任意截面的计算载荷为：

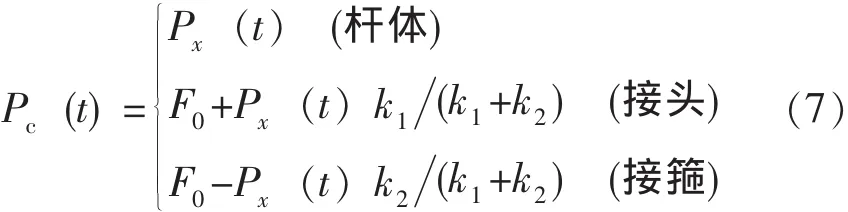
式中F0——螺纹连接的预紧力，N;

k1——接头刚度;

k2——接箍刚度。

根据轴向载荷的分析结果，可以知道截面最大的轴向载荷Pxmax和最小的轴向载荷Pxmin，并可进一步确定截面最大的轴向计算载荷Pcmax和最小的轴向计算载荷Pcmin，因而截面的最大应力、最小应力、应力幅值和平均应力为：

式中Ac——杆体、接头或接箍的横截面积，m2。

考虑应力集中系数的影响，抽油杆柱计算截面的等效应力幅值为[4]：

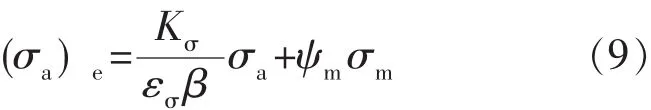
式中Kσ——应力集中系数；

εσ——尺寸系数；

β——表面状态系数；

ψm——敏感性系数。

应用 ANSYS软件对含斑坑、裂纹的抽油杆应力集中系数进行了分析和计算。应力集中系数与斑坑和裂纹的深度的回归关系为：

式中a0、a1、a2、b0、b1、b2——回归系数;

h——裂纹或斑坑深度，mm。

由σ-N曲线可知，在有限寿命的区间内，抽油杆柱的寿命计算公式为[5]：

式中N0——应力循环的基数，N0=107;

m——材料常数;

σr——疲劳极限，MPa;

r——应力比，r=σmin/σmax。

考虑抽油杆过渡段疲劳极限降低的影响，疲劳极限σr的计算公式为：

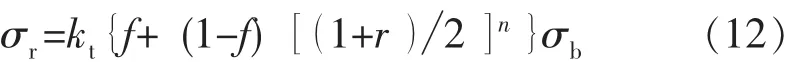
式中kt——疲劳强度影响系数;

σb——材料的抗拉强度极限，MPa;

f——疲劳比，f=σ-1/σb;

σ-1——材料的对称循环疲劳极限，MPa;

n——材料的常数，n=1/(ef);

e——待定的系数，e=1.66。

2 抽油杆柱疲劳寿命的可靠性预测模型

2.1 杆柱任意截面疲劳寿命的可靠性预测模型

疲劳寿命的预测模型考虑了有关变量随机性的影响。表1给出了每个随机变量及其分布规律。

表1 随机变量及其分布规律

采用蒙特卡洛抽样理论对各随机变量进行抽样，将每一组中的随机变量的抽样值代入式 (11)，可求出计算截面的疲劳寿命值 Ni。拟合Ni可以求得疲劳寿命的概率密度函数以及计算截面的失效率。杆柱计算截面的失效率表示为威布尔分布：

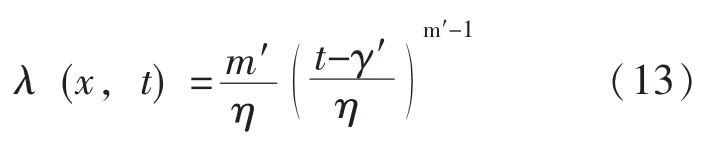
式中 λ(x，t)——截面的失效率;

x——截面到井口的距离，m;

m＇、η、γ＇——待定的系数，为x的函数。

抽油杆柱x截面处的寿命可靠性预测模型为：

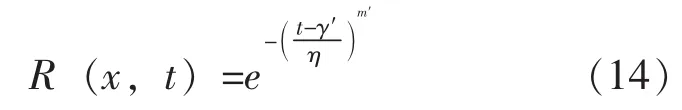
2.2 整体杆柱疲劳寿命的可靠性预测模型

假设抽油杆柱是由N′根抽油杆构成，可以将整个杆柱简化为由N′个元件构成的串联的系统。那么对于每单根抽油杆，可以将其简化为由杆体、过渡段、接头和接箍组成的子串联系统。因此，整体杆柱的失效率为：

式中 λi——第i根杆在寿命t时的失效率;

λbi——第i根杆杆体在寿命t时的失效率;

λti——第i根杆过渡段在寿命t时的失效率;

λci——第i根杆接头在寿命t时的失效率；

λji——第i根杆接箍在寿命t时的失效率。

根据可靠度和失效率的关系，由式 （14）计算整体杆柱在不同寿命下的可靠度。

3 抽油杆经济使用年限的可靠性评价模型

设T为使用年限。使用年限为T时油井的作业次数N(T)可表达为：

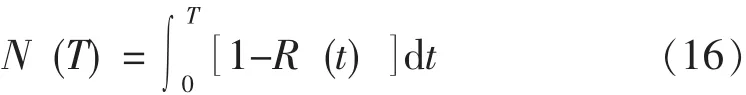
在使用年限T内，油井检泵作业费用Y1(T)、作业减产损失费用Y2(T)和投资费用Y3(T)分别为：

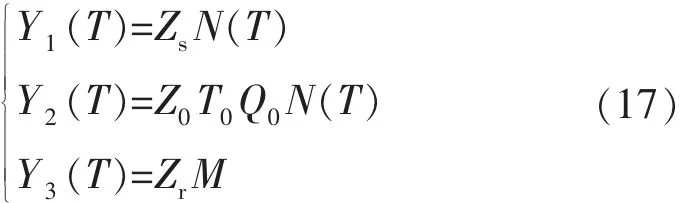
式中Zs——费用，元/次；

Q0——日产量，t/d;

Z0——价格，元/天；

T0——停产天数，d；

Zr——单价，元/千克;

M——总质量，kg。

抽油杆寿命周期内的年平均费用为：

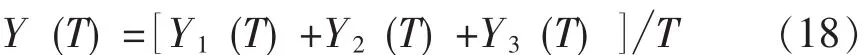
将年平均费用最低点所对应的使用年限定义为抽油杆的经济使用年限，即求式 （18）最小值所对应的年限。

4 抽油杆柱经济使用年限的可靠性仿真分析实例

仿真计算参数为：抽油机型号CYJI4-5.5-89HB，冲程5.5 m，冲次5 min-1，泵径44 mm，杆柱组合 25 mm×656.12 m+22 mm×747.03 m+19 mm×1196.83 m，沉没度500 m，D级抽油杆，含水质量分数85%，油压0.5 MPa，套压0.4 MPa，油气比30 m3/m3，饱和压力15.9 MPa。按API方法校核杆柱强度，泵径28 mm，杆柱应力使用系数SF=0.85。

取式 （17）中各参数值为Zs=3万元/次，Q0=3 t/d， Z0=5850元/天， Ts=5 d， Zr=10 元/千克， M=7420 kg。年均费用随使用年限的变化规律如图1所示。

图1 年均费用随使用年限的变化规律

从图1可以得出：①使用年限增加，年均作业费用逐渐增加，抽油杆年均投资费用逐渐降低；②在使用年限为8.732 a时，年均费用最小，为0.976万元。

5 结论

本文应用ANSYS有限元软件对含斑坑和裂纹的抽油杆的应力集中系数进行了分析计算；根据抽油杆柱受力情况，求得抽油杆柱任意截面的载荷，并结合疲劳累积损伤理论对抽油杆柱进行了疲劳寿命的可靠性预测。本文综合考虑抽油杆使用寿命期内抽油杆柱的投资费用、作业费用和作业产量损失费用，以使用年限内年均总费用最低为目标，建立了抽油杆柱经济使用年限的可靠性评价方法。

[1] 赵焕卿.抽油杆断裂失效分析 [J].石油矿场机械，2007，36 (7) ：60－61.

[2] 李其，刘殿魁，李晓秋.在用抽油杆服役期限的确定方法 [J].东北林业大学学报，2006，34(1)：111－114.

[3] 董世民.抽油机井动态参数计算机仿真与系统优化[M].北京：石油工业出版社， 2003：57－ 72.

[4] 徐灏 .疲劳强度设计 [M].北京：机械工业出版社，1981： 67－98.

[5] 宋保维 .系统可靠性设计与分析 [M].西安：西北工业大学出版社，2008：187－261.