内部爆炸作用下多层钢筒的动态响应*

崔云霄，胡永乐，王春明，胡 昊，陈鹏万

(1.北京理工大学爆炸科学与技术国家重点实验室，北京 100081; 2.西北核技术研究所，陕西 西安 710024; 3.长沙理工大学，湖南 长沙 410114)



内部爆炸作用下多层钢筒的动态响应*

崔云霄1,2，胡永乐3，王春明2，胡 昊2，陈鹏万1

(1.北京理工大学爆炸科学与技术国家重点实验室，北京 100081; 2.西北核技术研究所，陕西 西安 710024; 3.长沙理工大学，湖南 长沙 410114)

为评估内部爆炸作用下多层钢筒结构的防护效果，考察多层钢筒结构动态响应和变形吸能特征，采用两端开口、总厚度为50 mm的4层圆柱形Q345钢筒，在8.90～18.18 kg TNT药量下进行爆炸实验，并在容器外壁进行应变电测。实验后钢筒结构爆心局部发生塑性变形，内层钢筒变形最大，但未发生破坏。根据研究得到初步认识：采用爆心单位环面变形吸能的设计方法，可以较好地预估给定药量下所需钢筒的厚度；不同药量下，轴向距离超过多层钢筒结构的1/4内径后，其外壁环向变形峰值约减小为爆心截面环向应变峰值的1/2。

固体力学；多层钢筒；内部爆炸；动态响应；塑性变形

如何有效抵抗内部强爆炸的破坏效应，特别是较小装药比例半径下近区的强爆炸破坏一直是工程防护研究的热点，目前发展有爆室或爆炸容器等多种工程途径。作为一种危险限域装置，爆炸容器一般按照等效静载法换算爆炸超压，再按照压力容器有关标准进行强度设计，容器响应必须是弹性的[1-2]。这样，如果需在较大药量下使用，将使得设计容器的质量较大、运输困难、成本较高。为了提高其承载能力，一般是设法减小作用于壁面的冲击波强度，可以采取增大容器内部空间，或者填充泡沫铝、沙等多孔材料[3-5]，或者降低容器内初始气压等方法。有研究者采用钢筒外包裹混凝土材料进行加固[6]，取得了较好的效果。

增大容器壁厚是提高承载能力更直接的措施，但是采用厚壁结构时，金属材料特别是钢的脆性明显增强[7]。为了解决这一问题，可采用多层结构形式的爆炸容器[8-10]，内层和外层分别按不同变形准则进行结构和强度设计，让内层结构在爆炸载荷作用下充分变形，吸收爆炸冲击能量，外层结构保持弹性变形。实际上，可以考虑将外层结构的变形限制在一定范围，各层均发生塑性变形，以充分利用材料的变形吸能能力。研究这样一种多层结构在内部强爆炸作用下的动态响应，对于设计性能良好、效费比高的爆炸容器或防护结构具有重要意义。

1 实验装置设计

根据已开展的爆炸容器实验可知[8,11-12]，长径比大于2的圆柱形爆炸容器中，与装药同一截面(即爆心截面)部位承受载荷最大、形变最大，是整个容器结构的薄弱部位。本文中工作主要考虑该部位的抗爆性能。下面分析给定药量下，爆心截面部位允许塑性变形时所需的壁厚。假设爆炸冲击波作用到钢筒爆心单位环面的比冲量Ir被钢筒吸收并转化为塑性形变能Is，即有：

(1)

在爆炸冲击波作用下，可以近似认为钢筒爆心截面的单位环面获得一个初始膨胀速度，即：

(2)

式中：ρs为钢的密度，h为钢筒壁厚，v0为钢筒膨胀速度。根据能量守恒，爆心截面的单位环面获得的动能全部转化为塑性形变能，假设钢材料服从刚塑性本构关系(忽略弹性形变能的影响)，则有：

(3)

式中：σm为钢筒爆心截面的单位环面等效屈服应力，εm为钢筒爆心截面的单位环面塑性应变。由式(2)～(3)可知，所需的壁厚为：

(4)

由于金属钢在冲击载荷下会表现出屈服强度提高及屈服现象滞后等应变率效应，预估钢筒厚度时，需要考虑应变率效应的影响。钟方平[8]对16MnR材料进行应变率为40～50s-1的冲击拉伸实验结果表明，16MnR材料的动态屈服极限为600～800MPa。

反射超压比冲量的预估参考林俊德院士提出的经验公式[13]：

(5)

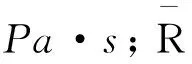
这里，钢筒的内直径取0.8m，动态屈服极限取为600MPa，塑性变形取2%，9、18.2kgTNT球形装药对应的比例距离分别为0.2、0.152m/kg1/3，按式(4)估算，9kg装药爆炸下钢筒所需厚度约为3.6cm，18.2kg装药爆炸下钢筒所需厚度约为6.8cm，其中18.2kg装药的反射超压比冲量是由公式(5)外推获得的。

根据以上分析，实验装置采用两端开口多层圆柱形结构，总厚度50mm，材料为Q345钢。装置的总装配长度为1 600mm，由3层内筒和1层外筒组成，其中内筒内径分别为800、830、860mm，长度均为1 000mm，厚度均为10mm；外筒内径890mm、长1 600mm、厚20mm。装置示意图如图1所示。实验装置装配出厂时，采取点焊措施在两端固定内层钢筒，保证各层的间距为5mm。

图1 多层钢筒结构示意图Fig.1 Schematic diagram of the multi-layer steel cylinder

2 爆炸实验及结果分析

实验时，将结构支承于地面。对4套装置共进行4次实验，采用球状TNT炸药，药量分别为8.90、8.90 、10.91和18.18 kg。在药球中制作传爆药柱，采用雷管在中心起爆。为减少炸药安装支架对爆炸流场的影响，制作木制三角支架支撑定位，使炸药安装后处于中心“悬浮”状态，中心尽量与钢筒轴心线重合。在外筒外壁面用应变片监测环向应变和轴向应变，共设8个测点，其中环向应变测点6个(爆心位置：应变片1、3、5，距离爆心20 cm位置：应变片2、4、6)，轴向应变测点2个，分布于爆心环面和距离爆心20 cm处的环面。环向应变测试数据如图2～3，由于在18.18 kg装药爆炸下，爆心环面的应变片全部被震飞，图3(c)只给出了距离爆心20 cm处的环向应变测试结果。作为参考，图4给出了8.90、10.91 kg装药量下爆心环面的轴向应变时程。

图2 爆心处的环向应变时程Fig.2 Hoop strain curves at explosion center

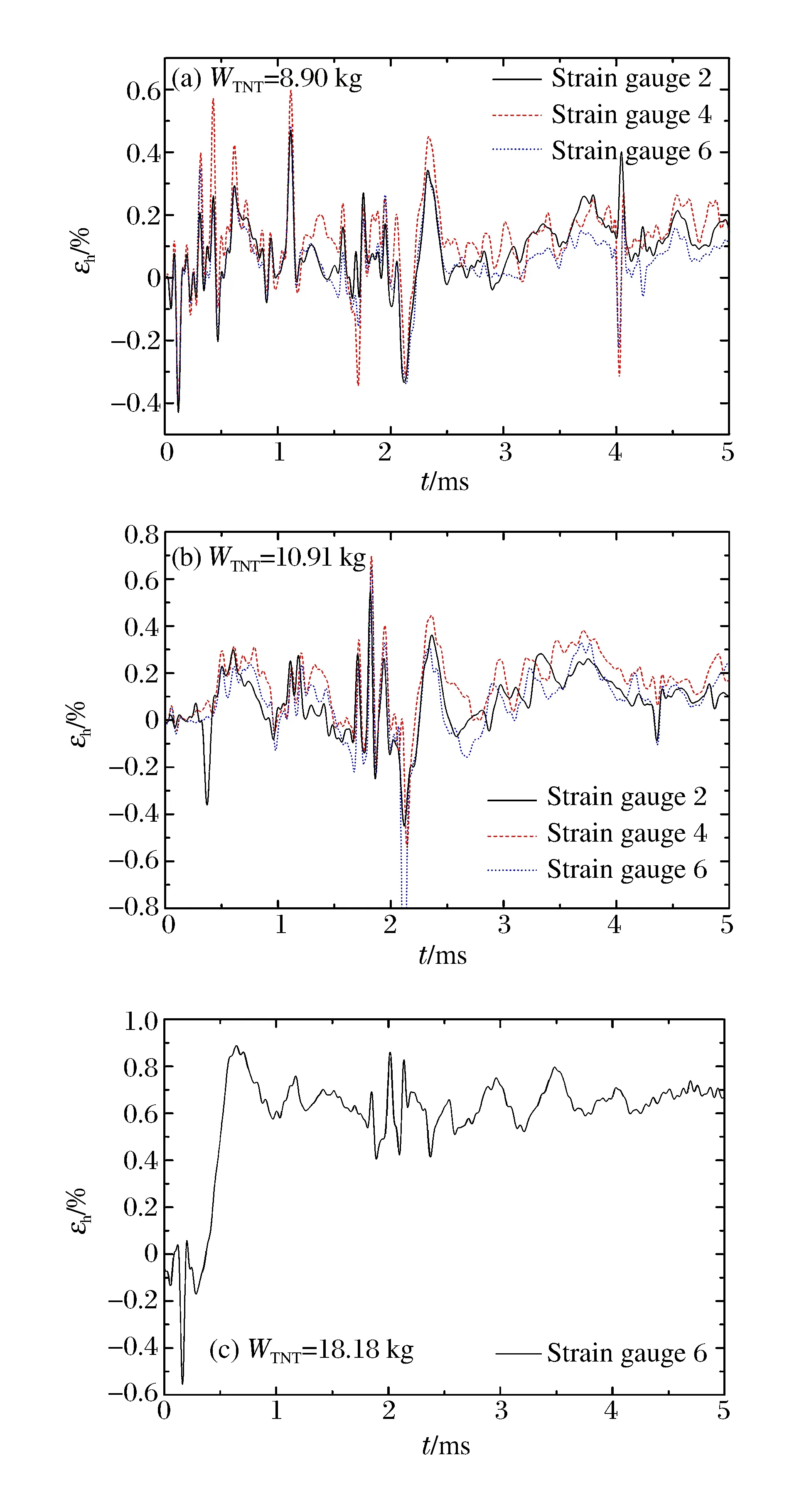
图3 距离爆心20 cm处的环向应变时程Fig.3 Hoop strain curves at 20 cm from explosion center

从图2可以看出，在起始阶段，外筒的环向应变时程含有较多干扰。8.90 kg装药爆炸下，外筒残余环向应变均值约0.24%；10.91 kg装药爆炸下，残余环向应变均值约1.3%。2种装药下，应变片3测得的残余变形均偏高，可能是由装药偏心导致的。

从图3(a)～(b)可以看出，距爆心20 cm处的环向应变峰值降低为爆心截面环向应变峰值的1/2以下，说明外筒的环向应变由爆心截面沿轴向逐渐降低。在2种药量下，距离爆心20 cm处外筒存在约0.1%的塑性变形。从图3(c)可以看出，当装药量增加到18.18 kg时，距离爆心20 cm处的外筒出现了约0.6%的塑性变形。比较图2、4看出，轴向应变的首波峰值约为环向应变首波峰值的2倍。

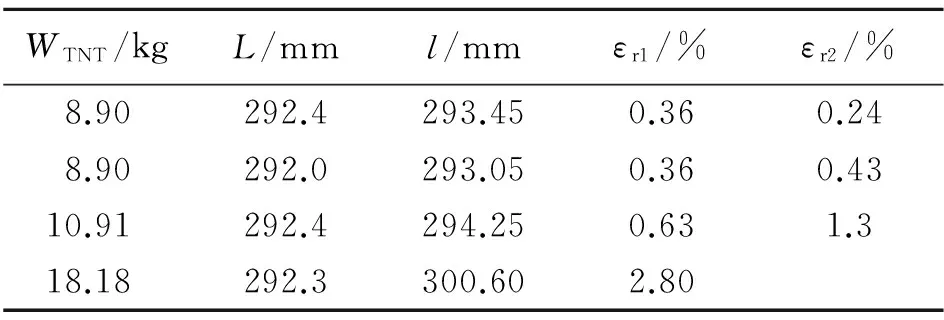
为了对比，测量钢筒结构在实验前后外筒爆心环面的周长变化作为残余塑性变形，如表1所示,表中WTNT为药量,L为初始外筒周长,l为爆后外筒周长,εr1为换算的残余变形,εr2为应变电测残余变形。

从表1可以看出，应变片电测结果逐渐趋于残余变形数据，两者一致性较好。在8.90 kg装药爆炸下，外筒有0.36%的残余变形；在10.91 kg装药爆炸下，外筒有0.63%的残余变形；在18.18 kg装药爆炸下，外筒残余变形达2.8%。据实验后观察，在8.90 kg装药爆炸时，实验装置的外表面没有肉眼可见变形，但内层钢筒出现明显塑性变形。当药量增大到18.18 kg时，钢筒外表面粘贴的应变片几乎全部被震飞，爆心截面位置出现肉眼可见的塑性鼓突，最内层钢筒爆心部位虽然有较大变形，但未出现宏观裂纹。根据实验可以看出，总厚50 mm的多层钢筒结构可以对装药量小于18.18 kg TNT球形装药爆炸起到较好的防护。

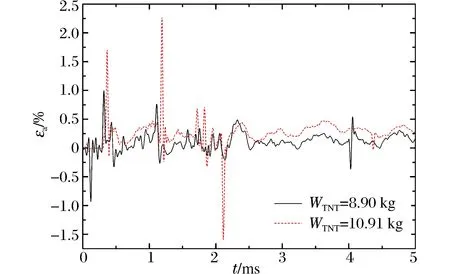
图4 爆心环面的轴向应变时程Fig.4 Axis strain curves at explosion center

WTNT/kgL/mml/mmεr1/%εr2/%8.90292.4293.450.360.248.90292.0293.050.360.4310.91292.4294.250.631.318.18292.3300.602.80

在应变电测中，有一些值得讨论的结果。在环向应变的开始出现拉伸应变之前，存在一个小幅值的压缩信号。这主要是由于多层钢筒的载荷作用方式与单层钢筒不同造成的。单层钢筒在内部爆炸作用下，筒体首先处于拉伸状态，然后呈现拉压交替变化，即环向应变是先拉后压的特征。如果钢筒发生塑性变形，则在首波峰值后在塑性变形位置附近呈现拉压交替的小幅度脉动。而多层结构形式下，爆炸冲量通过内部各层钢筒传递到最外层，各层钢筒先发生塑性变形，再通过层层之间碰撞向外传递能量，这样，外层钢筒先受到来自内部的冲击压缩，再发生向外膨胀，使得环向应变出现先压缩再拉伸的变形特征。另外，8.90、10.91 kg装药量爆炸下测得的轴向应变的首波峰值大于同位置环向应变的首波峰值，应该也与多层结构形式下载荷的作用方式有关，具体机理还需要进一步做工作。根据经验，单层筒体在内部爆炸作用下，同位置的轴向应变与环向应变大小一般是同量级的，如果没有发生塑性变形，轴向应变一般约为环向应变的1/2。

3 结 论

(1)采用爆心单位环面塑性变形吸能的设计方法，可以较好地预估给定药量下爆心截面所需防护钢筒的厚度。在上限药量爆炸下，钢筒结构各层发生不同程度的塑性变形，但未发生开裂破坏。(2)测试结果表明，轴向距离超过钢筒结构的1/4内径后，其外筒的环向变形峰值减小为爆心截面环向应变峰值的1/2，该位置的多层钢筒的总厚度可以考虑适当减薄。考虑到现场工程边界条件，如爆炸冲击载荷的冲量参数、钢筒允许的塑性变形量等，多层钢筒分层方式和层间间距还可以进一步调整优化。

[1] 赵士达.爆炸容器[J].爆炸与冲击,1989,9(1):85-96. Zhao Shi-da. Blast chamber[J]. Explosion and Shock Waves, 1989,9(1):85-96.

[2] 胡八一,柏劲松,刘大敏,等.爆炸容器的工程设计方法及应用[J].压力容器,2000,17(2):39-41. Hu Ba-yi, Bai Jin-song, Liu Da-min, et al. The engineering design method of explosion-containment vessel and its application[J]. Pressure Vessel Technology, 2000,17(2):39-41.

[3] Ashby M F, Evans A, Fleck N A. Metal foams: A design guide[M]. Stoneham, MA: Butterworth-Heineman, 2000.

[4] 周刚,唐玉志,关锦清,等.允许塑性变形爆炸容器的设计及实验探索[J].北京理工大学学报,2003,23(增刊):267-272. Zhou Gang, Tang Yu-zhi, Guan Jin-qing, et al. Explore of design and experiments for plastically deformed explosion containment vessels[J]. Transactions of Beijing Institute of Technology, 2003,23(suppl):267-272.

[5] Cui Yun-xiao, Hu Yong-le, Wang Wan-peng, et al. Experimental analysis of a sand tamped explosion vessel[C]∥Huang Feng-lei. Proceedings of the 7th International Conference on Shock & Impact Loads on Structures. Beijing, 2007:187-194.

[6] Wang Wan-peng, Hu Yong-le, Lin Jun-de, et al. Experiments and numerical analyses on dynamic deformation of steel-concrete structure under internal intense blast loading[C]∥Huang Feng-lei. Proceedings of the 7th International Conference on Shock & Impact Loads on Structures. Beijing, 2007:613-620.

[7] Taylor G I. The fragmentation of tubular bombs[M]∥The Scientific Papers of Sir G. I. Taylor. Cambridge: Cambridge University Press, 1963:387-390.

[8] 钟方平.双层圆柱形爆炸容器的弹塑性力学问题的实验和理论研究[D].合肥:中国科学技术大学,1998.

[9] 钟方平,马艳军,张德志,等.多层圆柱形钢筒在球形和柱形装药爆炸作用下塑性变形的研究[J].兵工学报,2009,30(增刊2):194-196. Zhong Fang-ping, Ma Yan-jun, Zhang De-zhi, et al. Research on plastic deformation of multi-layer cylindrical steel tube subjected to blasts of spherical and cylindrical charges[J]. Acta Armamentarii, 2009,30(suppl 2):194-196.

[10] 郑津洋,邓贵德,陈勇军,等.离散多层厚壁爆炸容器抗爆性能试验研究[J].爆炸与冲击,2005,25(6):506-511. Zheng Jin-yang, Deng Gui-de, Chen Yong-jun, et al. Experimental investigation on dynamic response and fracture characteristics of discrete multilayered thick-walled explosion containment vessels[J]. Explosion and Shock Waves, 2005,25(6):506-511.

[11] Pastrnak J W, Henning C D, Switzer V A, et al. Seal monitoring system for an explosive containment vessel[R]. LLNL: UCRL-CONF-205421, 2004.

[12] 穆朝民,任辉启,李永池,等.爆室内爆炸流场演化与壳体动力响应研究[J].振动与冲击,2009,28(10):106-111. Mu Chao-min, Ren Hui-qi, Li Yong-chi, et al. Blast flow field evolution and dynamic response of a blast chamber[J]. Journal of Vibration and Shock, 2009,28(10):106-111.

[13] 霍宏发.组合式爆炸容器动态特性分析及实验研究[D].西安:西安交通大学,2000.

(责任编辑 曾月蓉)

Dynamic response of multi-layer steel cylinder under internal intense blast loading

Cui Yun-xiao1,2, Hu Yong-le3, Wang Chun-ming2, Hu Hao2, Chen Peng-wan1

(1.StateKeyLaboratoryofExplosionScienceandTechnology,BeijingInstituteofTechnology,Beijing100081,China; 2.NorthwestInstituteofNuclearTechnology,Xi’an710024,Shaanxi,China; 3.ChangshaUniversityofScience&Technology,Changsha410114,Hunan,China)

In order to evaluate the protective effect and analyze the dynamic response of multi-layer steel cylinder under internal blast loading, we have conducted four experiments, with three different charge mass, ranging from 8.90 to 18.18 kg. The multi-layer steel cylinder we used is composed of 4 layers made of Q345 steel. The 4 layers altogether are 50 mm in thickness, with the 3 inner ones as 10 mm and the outer one as 20 mm respectively. The diameter of the innermost layer is 800 mm and the distance between layers is 5 mm. At the section of charge center and 20 cm axial distance from the charge, the hoop strain and axial strain are measured by eight strain gauges set on the outside of steel shell. Under the blast loading, the plastic deformation occurred locally at the charge center, and the largest deformation appeared at the innermost layer. However, even in the circumstance of the largest charge mass, there is no failure. It is concluded that the thickness of the steel cylinder could be predicted accurately with the energy absorbing design method applied to the unit section of the charge center of the multi-layer steel cylinder. With a proper change in charge mass, the peak hoop strain can reduce to about 1/2 of the section at the charge center, when the axial distance is beyond the 1/4 diameter of the inner layer.

solid mechanics; multi-layer steel cylinder; internal blast loading; dynamic response; plastic deformation

10.11883/1001-1455(2015)06-0820-05

2014-04-14；

2014-10-16

崔云霄(1980— )，男，博士研究生,yunxiaocui@163.com。

O347.3 国标学科代码： 13015

A