低马赫数下斜爆轰波的结构*
2015-04-12王健平
刘 岩,武 丹,王健平
(1.北京大学工学院力学与工程科学系,北京 100871;2.北京大学工学院湍流与复杂系统国家重点实验室,北京 100871)
低马赫数下斜爆轰波的结构*
刘 岩1,2,武 丹1,2,王健平1,2
(1.北京大学工学院力学与工程科学系,北京 100871;2.北京大学工学院湍流与复杂系统国家重点实验室,北京 100871)
利用Euler方程和两步化学反应模型,对低马赫数入流时的驻定斜爆轰波进行了数值模拟,并重点研究了斜爆轰波的驻定过程和结构。数值结果显示,当入流马赫数较低时,即使其本身是附体的,在诱导区后侧的高压区的作用下,斜爆轰波也会从其起始位置向来流方向运动。在这种情况下,斜爆轰波会驻定在靠近斜面前缘的位置,诱导区的长度仅有1 mm左右。通过设置初始条件,让斜爆轰波在斜面前缘附近被触发,则其将一直维持在靠近斜面前缘的位置。
爆炸力学;诱导区;Euler方程;驻定斜爆轰波;低马赫数入流
爆轰是一种近似等容的燃烧方式,与现在广泛使用的爆燃相比,其燃烧速率更快、热效率更高。作为一种在高超声速推进系统中有巨大应用潜力的燃烧方式,斜爆轰波受到了广泛的关注。已经有通过数值模拟、实验和理论分析等对其进行的广泛研究[1-6]。
C.Li等[1]通过数值模拟发现了斜爆轰波的基本结构,即:斜激波、诱导区、爆燃波、斜爆轰波。斜激波、诱导区和斜爆轰波在实验中均可以明显观察到[2-6]。但是爆燃波的存在依然存在疑问,因为它的存在与实验中广泛观察到的诱导区后侧斜爆轰波被增强的现象[2-6]相矛盾。在D.Desbordes等[4]、C.Viguier等[5]的实验中,可以看到诱导区后侧是一个激波而非一系列的爆燃波。在对驻定在双楔面上的斜爆轰波进行理论研究时,K.Ghorbanian等[7]提出诱导区后侧是一个CJ斜爆轰波。但是,到目前为止,这一模型还没有被实验直接验证。
在对钝头锥体所触发的斜爆轰波进行数值模拟时,M.H.Lefebvre等[8]发现当入流速度较低时,斜爆轰波会从其起爆位置向来流方向运动,并最终驻定在锥体前缘。通过对由斜面触发的斜爆轰波进行数值研究,L.F.F.da Silva等[9]也发现了类似的现象,但是他们并没有给出斜爆轰波驻定下来时的流场状况。由于低马赫数入流时斜爆轰波最终会驻定在斜面前缘,因而可以用很短的斜面来维持它,进而可以大幅度的减小斜面所引起的阻力。这对于斜爆轰波在超声速推进系统中的应用是非常有利的。由于M.H.Lefebvre等[8]、L.F.F.da Silva等[9]均仅提供了一个算例,没有有效的对照和分析。因此,到目前为止,低马赫数入流时斜爆轰波会从其起爆位置前移的根本原因依然不清楚,并且对于其驻定结构的特征也缺乏了解。本文中,通过数值模拟,对低马赫数入流时的斜爆轰波进行系统的分析和研究,以期对其驻定过程和驻定结构有更深入的了解。
1 数值方法和物理模型
由于黏性对于斜爆轰波结构的影响十分有限[10],采用含两步化学反应[11]源项的笛卡尔直角坐标系中的Euler方程作为控制方程:

参数k1、k2、E1、E2取值见文献[11]。本文中所采用的入流气体均为101.325 kPa、292 K的当量比的氢氧均匀混合气体。
斜爆轰波的计算域及其结构的示意图如图1所示,x轴和y轴分别与斜面平行和垂直。在x轴和y轴方向均采用均匀离散网格,网格大小均为0.02 mm。对流项采用5阶WENO格式[12]求解,时间积分采用3阶Runge-Kutta格式求解。在斜面上采用滑移边界条件,在左侧和上侧边界采用入流条件,右侧边界条件通过把内侧的流场参数梯度取为零得到。

图1 斜爆轰波计算域及其结构示意图Fig.1 Schematic representation of computational domain and oblique detonation wave configuration
2 结果与讨论
为了研究低马赫数入流时斜爆轰波从起爆位置前移的原因,把斜面所引起的斜激波作为数值模拟的初始条件,氢氧混合气体由上侧和右侧边界进入计算区域。图2是来流马赫数(Ma)0=6.6、斜面角度θ=26°时,斜爆轰波起爆并形成稳定向前传播结构的过程。由于在斜激波后流场是定常的均匀流场,流场内诱导反应进行的速度相同。而越靠近斜面的氢氧混合气体,其在斜激波后的流场内所经历的时间越长。因此,靠近斜面的氢氧混合气体的诱导反应最先结束,其释热反应也最先开始。如图2(a)所示,由于斜面附近氢氧混合气体的释热反应,在壁面附近形成一个近似半圆形的燃烧波。这个燃烧波逐渐向斜激波方向传播,并最终与之耦合而形成如图2(b)所示的斜爆轰波。由图2(b)、2(c)和2(d)可以看到,斜爆轰波并没有驻定在其起始位置,而是逐渐向前传播。由图2(c)可以看到,随着斜爆轰波向前传播,诱导区后侧的燃烧波会发生褶皱而形成一个近似对称的激波反射结构。并且随着斜爆轰波前移,这个激波反射结构逐渐向壁面方向移动。在其下移的过程中,下侧的燃烧波始终驻定在它的初始位置。由这个现象可以知道,诱导区后的燃烧波本身是驻定的。由图3可以看到,斜爆轰波最终驻定在了斜面上,因此斜爆轰波本身也是驻定的。由此可以知道,斜爆轰波的前移不可能由单个激波的脱体引起,而只可能由激波间的相互作用引起。

图2 当(Ma)0=6.6、θ=26°时斜爆轰波的压力场Fig.2 Pressure field of oblique detonation wave at (Ma)0=6.6, θ=26°

图3 斜爆轰波驻定时的压力场Fig.3 Pressure field of stabilized oblique detonation wave

图4 诱导区后侧的压力场Fig.4 Pressure contours behind induction region
图4是图2(d)中诱导区后侧燃烧波附近的压力场云图。由图4可以看到,诱导区后侧的气体压强非常高,这是因为诱导区后的气体经过了斜激波和燃烧波的两次增压作用。经过燃烧波后的膨胀波后,压强依然明显高于入流马赫数为6.6时斜爆轰波的脱体压强3.03 MPa。由于斜爆轰波和诱导区后的燃烧产物仅由一个接触间断隔开,而接触间断两侧压强相同,所以此时的斜爆轰波会发生脱体而前移。因此可以做出结论:来自诱导区后的高压区的影响是导致斜爆轰波脱体的原因。当斜爆轰波最终驻定时,总是驻定在非常靠近斜面前缘的位置,此时诱导区的长度仅有1 mm左右。例如,当斜面角度为27°、入流马赫数为6.6、6.8和7.0时,诱导区的长度分别为0.7、1.0和2.2 mm。根据C.Li等[10]关于边界层对斜爆轰波结构的影响的研究,当考虑黏性等对斜爆轰波结构的影响时,诱导区的长度还会稍微减小。这对于斜爆轰波的应用是非常有利的,因为诱导区越小,所需使用的斜面长度也就越小,斜面所引起的阻力也就会越小。
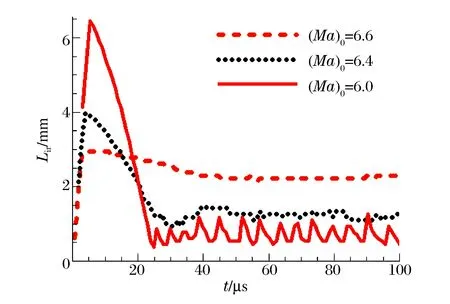
图5 诱导区长度Fig.5 Length of the induction region
虽然在低马赫数入流时,斜爆轰波最终会驻定在非常靠近斜面前缘的位置。但是由图2可以看到,当采用与入流条件相对应的斜激波作为初始条件时,触发斜爆轰波所需要的斜面长度很大,这会引起很大的阻力。所以,能否在壁面前缘附近人为的触发斜爆轰波,并且使它一直维持在斜面前缘附近,对于这类斜爆轰波的应用非常重要。为了研究在斜面前缘附近被触发的斜爆轰波能否维持在靠近斜面前缘的位置,把数值模拟的初始条件设置为一个不稳定的速度间断。因为斜爆轰波的前端与诱导区的后侧相连,因此通过记录诱导区的长度观察斜爆轰波的位置。图5是从初始时刻开始诱导区长度随着时间的变化曲线。由图5可以看到,斜爆轰波在斜面前缘附近被触发后,一直维持在斜面前缘后侧1 cm以内。由此可以知道,在斜面前端被触发的斜爆轰波可以一直维持在比较靠前的位置。图6是(Ma)0= 6.2时驻定斜爆轰波诱导区附近的压力云图。由图6可以看到,在诱导区后侧的单向三波区域[13]内,爆轰波面上的横波逐渐向前传播。当横波运动至诱导区时,它会使诱导区后侧的燃烧波增强,进而导致诱导区长度减小。当横波引起的影响被减弱后,诱导区的长度则会随之增加。这样就产生了如图5所示的诱导区长度随时间变化而发生震荡的现象。但是,随着入流速度的增加,横波向前传播的现象会受到抑制,对诱导区的影响也会减弱。因此,随着入流速度的增加,诱导区长度的震荡逐渐减弱直至消失。

图6 当(Ma)0=6.2、θ=25°时驻定斜爆轰波诱导区附近的压力场Fig.6 Pressure field in vicinity of induction region of stabilized oblique detonation wave at (Ma)0=6.2, θ=25°
3 结 论
利用Euler方程和两步化学反应模型,对低马赫数入流时的驻定斜爆轰波进行了数值模拟,发现斜爆轰波的前移由来自诱导区后侧的高压区的影响引起。斜爆轰波最终总是驻定在非常靠近斜面前缘的位置,此时诱导区的长度仅有1 mm左右。由于诱导区越短,用来维持斜爆轰波的斜面就可以越短,这对于斜爆轰波的应用非常有利。通过设置初始条件使斜爆轰波在斜面前缘附近被触发,则被触发的斜爆轰波将一直维持在靠近斜面前缘的位置。这证明,对于低马赫数入流的情况,可以通过调整初始条件而让斜爆轰波始终维持在很靠前的位置。
[1] Li C, Kailasanath K, Oran E S. Detonation structure behind oblique shocks[J]. Physics of Fluids, 1994,6(4):1600-1611.
[2] Wang Ai-feng, Zhao Wei, Jiang Zong-lin. The criterion of the existence or inexistence of transverse shock wave at wedge supported oblique detonation wave[J]. Acta Mechanica Sinica, 2011,27(5):611-619.
[3] Verreault J, Higgins A J. Initiation of detonation by conical projectiles[J]. Proceedings of the Combustion Institute, 2011,33(2):2311-2318.
[4] Desbordes D, Hamada L, Guerraud C. Supersonic H2-air combustions behind oblique shock waves[J]. Shock Waves, 1995,4(6):339-345.
[5] Viguier C, da Silva L F F, Desbordes D et al. Onset of oblique detonation waves: Comparison between experimental and numerical results for hydrogen-air mixtures[J]. Proceedings of the Combustion Institute, 1996,26(2):3023-3031.
[6] Morris C I, Kamel M R, Stouklov I G, et al. PLIF imaging of the supersonic reactive flows around projectiles in an expansion tube[R]. American Institute of Aeronautics and Astronautics, 1996.
[7] Ghorbanian K, Sterling J D. Influence of formation processes on oblique detonation wave stabilization[J]. Journal of Propulsion and Power, 1996,12(3):509-517.
[8] Lefebvre M H, Fujiwara T. Numerical modeling of combustion processes induced by a supersonic conical blunt body[J]. Combustion and Flame, 1995,100(1):85-93.
[9] da Silva L F F, Deshaies B. Stabilization of an oblique detonation wave by a wedge: A parametric numerical study[J]. Combustion and Flame, 2000,121(1):152-166.
[10] Li C, Kailasanath K, Oran E S. Effects of boundary layers on oblique-detonation structures[R]. American Institute of Aeronautics and Astronautics, 1993.
[11] Korobeinikov V P, Levin V A, Markov V V, et al. Propagation of blast wave in a combustible gas[J]. Astronautica Acta, 1972,17(4):529-537.
[12] Balsara D S, Shu C W. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy[J]. Journal of Computational Physics, 2000,160(2):405-452.
[13] Gui Ming-yue, Fan Bao-chun, Dong Gang. Periodic oscillation and fine structure of wedge-induced oblique detonation waves[J]. Acta Mechanica Sinica, 2011,27(6):922-928.
(责任编辑 丁 峰)
Structure of oblique detonation wave at low inflow Mach number
Liu Yan1,2, Wu Dan1,2, Wang Jian-ping1,2
(1.DepartmentofMechanicsandEngineeringScience,CollegeofEngineering,PekingUniversity,Beijing100871,China;2.StateKeyLaboratoryforTurbulenceandComplexSystems,CollegeofEngineering,PekingUniversity,Beijing100871,China)
With the Euler equations and a two-step chemical reaction model, a numerical investigation of the wedge-induced oblique detonation wave (ODW) at low inflow Mach number is performed in this paper. Its stabilization process and stationary structure are studied in detail via numerical simulation. It is found that the upstream propagating of an attached ODW at low inflow Mach number is resulted from the effect of the high pressure region behind the induction region. In this condition, the ODW is always stable in the vicinity of the wedge tip. The length of the induction region is about one millimeter. When the ODW is triggered near the wedge tip, it will stay in its vicinity.
mechanics of explosion; induction region; Euler equation; oblique detonation wave; low inflow Mach number
10.11883/1001-1455(2015)02-0203-05
2013-07-05;
2014-02-17
刘 岩(1990— ),男,博士研究生,liuyandeyoux@126.com。
O381 国标学科代码: 1303510
A
