金属圆柱壳受大质量低速冲击的屈曲变形*

路国运,段晨灏,雷建平,韩志军,张善元

(太原理工大学材料强度与结构冲击山西省重点实验室,山西 太原 030024)



金属圆柱壳受大质量低速冲击的屈曲变形*

路国运,段晨灏,雷建平,韩志军,张善元

(太原理工大学材料强度与结构冲击山西省重点实验室,山西 太原 030024)

对钢质和铜质金属圆柱壳的轴向冲击动力响应进行了实验研究，记录了两种不同材料圆柱壳在大质量低速冲击下的冲击力时程曲线，得到其屈曲模态。采用高速摄像及模拟技术给出了钢质圆柱壳渐进屈曲的全过程，为理解钢质圆柱壳的屈曲机理提供了直观的结果。黄铜质圆柱壳在大质量低速冲击下,出现整个壳面滿布屈曲波纹的塑性动力屈曲现象，说明高速冲击不是产生塑性动力屈曲的充要条件。像铜这样具有高密度的韧性材料，在大质量低速冲击下，会在轴向产生持续的压缩塑性流作用而出现塑性动力屈曲现象。

固体力学；塑性动力屈曲；落锤；圆柱壳；塑性累进屈曲

在动力冲击下，圆柱壳展示出丰富的屈曲模态并表现出复杂的动力学行为以及很高的吸能效率[1-6]。N.Jones[1,3]指出，通常可以将圆柱壳在轴向冲击载荷作用的动态屈曲问题分为两类，即动力累进屈曲(dynamic progressive buckling)和塑性动力屈曲(plastic dynamic buckling)。所谓动力累进屈曲，即结构从一端开始屈曲，并向另一端渐进发展；一般认为其对应于较低冲击速度，通常可以忽略横向惯性力的影响。而塑性动力屈曲对应的冲击速度一般较高，这种情况下的屈曲波纹(几乎同时)遍布整个壳体，而不是像动态累进屈曲那样起先局限于冲击端而后向全长渐进发展。而D.Karagiozova等[7-8]的研究表明，应变率敏感性材料的圆柱壳只出现动力累进屈曲。路国运等[9]指出，横向惯性效应与应力波的相互竞争是出现塑性动力屈曲的关键因素，其他因素都可围绕这两个因素加以讨论。H.E.Lindberg等[10]在对细长杆和圆柱壳的弹性动力屈曲实验中，观察到了应力波效应对屈曲的影响，但在理论分析中,基于屈曲形成速度远小于应力波传播速度、屈曲是在应力波来回反射多次后形成这个假设，没有考虑应力波效应。D.H.Chen等[11]则指出，冲击端初始峰值载荷是与冲击速度相关的，而远端基本保持恒定。郑波等[12]采用双特征参数法对轴对称弹性动力屈曲问题进行求解。顾红军等[13]通过实验，研究了薄壁圆柱壳径厚比对屈曲波纹数的影响及其吸能性能。B.A.Gordienkor[14]在实验中注意到，轴向冲击下圆柱壳在一定条件下会发生非轴对称屈曲。王仁等[15-17]讨论了B.A.Gordienkor[14]的实验结果，并进行了一系列实验，指出圆柱壳在轴向冲击下有两种临界速度，对应于壳体发生轴对称屈曲和非轴对称非均匀屈曲。如上所述，圆柱壳冲击屈曲对各种条件的敏感性使问题非常复杂，仍有许多问题未能得到合理的解决。对于如何区分或在什么条件下产生动力累进屈曲还是动力塑性屈曲，目前仍未能有明晰的界定方式。D.Karagiozova等[8]和路国运等[9]在讨论中，均指出了冲击速度并不是出现塑性动力屈曲的必要条件，在适当的参数下低速冲击亦会出现塑性动屈曲现象，这个观点有待进一步的实验验证及研究。

本文中，对钢、铜质圆柱壳进行轴向冲击实验，得到不同的屈曲模态及冲击力时程曲线。实验显示，像铜这样的具有高密度的韧性材料，在并不高的冲击速度下出现塑性动力屈曲现象。为D.Karagiozova等[8]和路国运等[9]关于出现塑性动力屈曲条件的讨论，提供实验依据。

1 实验装置

图1 实验装置示意图Fig.1 Schematic arrangement

实验采用落锤式冲击加载试验机DHR-9401作冲击加载。采用压电传感器记录冲击力变化，并采用Koda高速摄像机(最高记录速度为2 000 s-1)实时记录钢管和铜管冲击动态响应的全过程。而瞬态位移采用米依公司的光电位移传感器opto NCDT 1605测量。图1为实验装置示意图。

2 实验结果

试件为结构用15CrMn无缝钢管，管壁厚1 mm，外径44 mm，长度为90～220 mm，屈服强度σ=368 MPa。铜管(HSn70-1)管壁厚1.2 mm，外径42 mm，长度为84、126和168 mm，屈服强度σ=250 MPa。落锤质量最大为201.8 kg，并在实验中进行了调整，冲击高度也对应不同冲击状态下圆柱壳的不同响应,而进行调整。

高速摄像记录及最终的变形模态显示，钢质圆管基本上先发生轴对称屈曲，后由于管壁变形相互作用及缺陷的影响，向非轴对称变形过渡。图2给出高度220 mm钢管受质量201.8 kg落锤在高1.5 m处以速度5.42 m/s冲击的冲击力曲线。由图可以看出：冲击力在冲击发生瞬间即达到一个极高的初始峰值,这个峰值引发圆柱壳在冲击端处产生第一个屈曲波纹，冲击力随后急剧下降,之后相对应于圆柱壳的累进屈曲，表现出有规律的上下波动起伏。这些波动是由于连续皱折形成的结果,每一个后来的峰值对应于一个皱折过程的开始，而在两个连续峰值之间有一个二级峰值，对于这个二级峰值偏心模型[18]可以给出很好的解释。实验屈曲模态数与其载荷峰值分布基本上吻合，8个峰值对应于钢质圆柱壳上的8个波纹。由于圆柱壳发生了由轴对称向非轴对称变形的转变，一个非轴对称波形变形的波长大于轴对称的，因此对应于每一个非轴对称屈曲波纹的冲击力时间比轴对称的长，冲击力峰值也相对平缓，其上下波动也不像轴对称的那样规律。但实验中并未出现从一开始就完全是非轴对称屈曲的模态。

图2 高220 mm钢圆管的冲击力曲线和屈曲模态Fig.2 Impact force cuver and buckling mode of 220 mm steel shell

图3给出了高度90 mm圆柱壳受到100 kg落锤以速度7.21 m/s撞击时的位移曲线。由图可知，圆柱壳的压缩位移相当平缓，未出现类似冲击力的锯齿状波动。结合位移-冲击力曲线可以看出：尽管冲击力出现了波动性，但在后续屈曲过程中是非常稳定的,冲击力基本在一定值处波动,轴向压缩变形基本成线性增长，这正是理想的吸能构件所要求的。本次冲击未发生变形模式由轴对称向非轴对称的转变，因此冲击力具有较好的波动规律。由于所用的圆柱壳高度较低，整个屈曲过程还未能消耗完冲击能量，之后落锤将屈曲后的变形体进一步压实，冲击力表现为又一个极高的峰值。

图3 高90 mm钢圆管的位移曲线、冲击力-位移曲线和屈曲模态Fig.3 Displacement curve, impact force-displacement curve and buckling mode of 90 mm steel shell

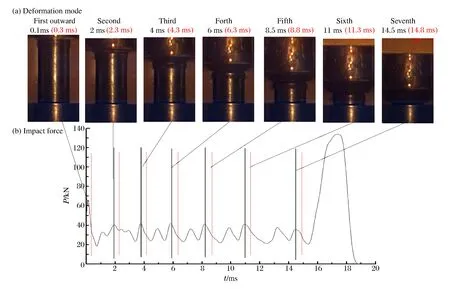
图4 高90 mm钢圆管的冲击力曲线和对应变形模态Fig.4 Impact force curve and deformation modes of 90 mm steel shell

为了解整个冲击过程中冲击力与屈曲模态的对应关系，图4给出了图3圆柱壳受冲击时由高速摄像拍到的不同时刻的变形图，并与冲击力曲线中对应时刻相对应。图中时间是由高速摄像按2 000 s-1速度拍摄的图按间隔幅数计算出来的，由于所取的第一幅图片不可能刚好是冲击发生的的初始时刻，因此由图4给出的对应关系存在一定的误差(可能冲击力和变形模态并不是同一时刻)。为清楚得到冲击力与屈曲模态波动的对应关系，进行了数值模拟，精确地给出同一时刻的冲击力点与屈曲的发展模态，如图5所示。由图可知，在0.1 ms时，冲击力有一个极大的峰值，而圆柱壳则未出现明显的外鼓变形，将变形图放大后可以看出圆柱壳在冲击端处有不明显的外鼓变形，说明这个初始冲击力峰值的主要抗力来自柱壳的轴向压缩并引发了第一个屈曲波纹的产生。之后圆柱壳在冲击端处出现明显的外鼓波纹，对应于突降的过程(这时壳壁的弯曲变形成为主要抗力，相对于轴向压缩弯曲变形刚度弱很多)；随着落锤的进一步下压，外鼓波形上半部分被压平，波形下半部分开始弯曲变形，这时冲击力经历了又一次的波动，即达到一个小峰值并开始下降，直到波纹的上下两部分被叠合。之后第二个波纹开始产生消耗剩余的冲击能量(对应于冲击力的突然上升)，并延续第一次波纹产生与发展的历程，如果冲击能量足够大，则会产生多个褶皱直到冲击能量被吸收，而冲击力则表现出有规律周期性的波动。比较图4～5，应对图4给出的变形图与冲击力的时刻对应作一些调整(图中红字及红虚线为做了调整后的)。因为，图4给出的是每个波纹已经明显发展时刻的模态图，而图5显示的是外鼓波纹明显出现时冲击力处于波谷或者下降的阶段。尽管实验中无法准确确定模态与冲击力的对应时刻，但模态的间隔时间可以推断，由图4给出的对应图可以看出屈曲波纹出现与冲击力波动的周期性有很好的对应，再加上数值模拟给出的结果相互验证，图4～5很好地说明了冲击发生时圆柱壳屈曲及吸能的变形机制。

图6 冲击端部第一个弧段内边缘节点轴向坐标曲线的数值模拟结果Fig.6 Simulation results of displacement curve of cylindrical shell near impact side

为进一步验证上述变形与冲击力之间的对应关系，给出了冲击端部第一个波纹区内外侧母线上节点(图中黑方框中包括的节点)的轴向坐标曲线(见图6)。由图可以看出：(1)在0～0.1 ms区间是平行区；(2)在0.4～0.7 ms和0.7～1.5 ms区间有两个交汇区。依据这些特点，并结合图5中的冲击力曲线，可以推断，在冲击初始时间(0～0.1 ms)内母线上各节点基本上以相同的速度向下移动(表现为各条线基本平行)，表示该区内的壳体发生轴向均匀的压缩变形；之后，不同的节点下移的速度发生了变化，靠近冲击端部的节点下移较快而远离冲击端的节点下移较慢，甚至有一点回弹(最下面的曲线在0.1～0.7 ms间是上凸)；这个阶段对应于圆管在冲击端部产生了第一个屈曲，圆管的响应主要以波纹长度内管壁的弯曲变形为主，其过程大致分为3个阶段：首先，屈曲波纹的靠近冲击端的上半部分发生弯曲，直到顶部的壳壁开始压弯到比临近部分壳壁位置低时(这时冲击力是一个下降的趋势)；之后，屈曲波纹的上半部分被压平(下半部分下移的位移也较明显)，对应于0.4～0.7 ms的交汇区(冲击力是一个上升的过程)；最后，屈曲波纹的上半部分压弯后随下半部分弯曲变形而下移，下半部分由于弯曲变形发生弯折，其靠上的部分也被压弯到比其下面临近部分位置低，即在0.7～1.5 ms间出现了又一个交汇区，最终这个弯曲的波纹被压扁而形成一个对折，这时一个冲击屈曲的周期结束(冲击力包含两次波动)。如果能量足够，圆柱壳开始第2个、第3个等冲击屈曲响应的冲击周期。如果整个冲击过程发生的都是轴对称的屈曲，则每一个周期冲击力都包含两次波动(如图4～5冲击力曲线所示)，如果发生了由轴对称向非轴对称转变的屈曲响应，则其冲击力的周期性被打破。与轴对称屈曲相比，一个非轴对称波纹有较大的波长，因此其响应的周期较长。

图7 高84mm铜圆管的冲击力曲线和屈曲模态Fig.7 Impact force curve and buckling mode of 84 mm copper shell

图7给出了铜质圆柱壳受轴向速度1.9 m/s冲击时的屈曲模态图，圆柱壳在整个壳面出现了不很明显的屈曲波纹。通过反光判断，在整个壳面上有7个波动产生，对应于其冲击力波动的7个峰值。与钢质圆柱壳的冲击力比较发现，其冲击力波动没有二次峰值出现，几个波动的峰值也基本接近，而不像钢质圆柱壳那样初始峰值远大于其他。比较持续的冲击时间发现，铜质圆管对应的波动时间在0.25 ms左右，而钢质圆管形成一个褶皱所需时间在2 ms左右，这相当于本次铜圆柱壳的整个冲击屈曲时间。初始冲击力峰值达到了52.3 kN左右，而在2 ms内屈曲波纹即在整个壳面上出齐，是典型的塑性动力屈曲现象。这说明，像铜这样的高密度韧性材料，在并不高的冲击速度下出现了塑性动力屈曲现象。

3 总 结

对钢、铜质圆柱壳进行了大质量低速冲击实验研究，得到了不同的屈曲模态及冲击力曲线，由两种不同材料的变形过程得到：钢质圆柱壳在本实验冲击速度下产生累进塑性屈曲变形，而铜圆柱壳则在很短时间内出现满布壳身的塑性动力屈曲。运用数值分析及高速摄像给出了钢质圆柱壳变形的详细过程，并与冲击力曲线进行了对比分析，给出了钢圆柱壳屈曲过程各阶段的响应特点：冲击力曲线显示，累进屈曲相应于一个波形的形成会使冲击力出现两个波峰；而铜质圆柱壳出现塑性动力屈曲，由于变形波形并未充分发展，对应于一个屈曲波纹的变形出现一个波动。

实验中选取了钢和铜两种材料的圆柱壳，相较而言，钢材料属于应变率敏感材料，而铜则属应变率不敏感材料。实验中，钢质圆柱壳总是产生累进屈曲，而铜质圆柱壳则在冲击短时间内出现了满布壳面的屈曲变形，其时间尺度相当于钢质圆管一个波形形成的时间。这与通常认为的塑性动力屈曲只能在高速冲击下才出现相矛盾。但这印证了D.Karagiozova等[8]和路国运等[9]关于累进屈曲与塑性动力屈曲的讨论，他们认为横向惯性效应与应力波的相互竞争是出现塑性动力屈曲的关键因素，如果材料参数合适，完全有可能出现低速冲击下的塑性动力屈曲现象。实验中像铜这样的具有高密度的韧性材料，在并不高的冲击速度下出现塑性动力屈曲现象，为D.Karagiozova等[8]和路国运等[9]关于出现塑性动力屈曲条件的讨论提供了实验依据。

[1] Jones N. Structural impact[M]. Cambridge, UK: Cambridge University Press, 1989.

[2] 陈铁云，沈惠申.结构的屈曲[M].上海:上海科学技术出版社,1993.

[3] Jones N. Recent progress in the dynamic plastic behavior of structures[J]. Journal of Applied Mechanics, 1989,42(2):95-115.

[4] 王仁.冲击载荷下结构塑性稳定性研究[C]∥冲击动力学进展.合肥:中国科学技术大学出版社,1992:157-176.

[5] 杨桂通，王德禹.结构的冲击屈曲[C]∥冲击动力学进展.合肥:中国科学技术大学出版社,1992:177-210.

[6] 唐柱才.冲击载荷下结构动态屈曲的数值研究[D].大连:大连理工大学，2004.

[7] Karagiozova D. Inertia effects on some crashworthiness parameters for cylindrical shells under axial impact[J]. International Journal of Crashworthiness, 2001,6(4):561-572.

[8] Karagiozova D, Jones N. Influence of stress waves on the dynamic progressive and dynamic plastic buckling of cylindrical shells[J]. International Journal of Solids and Structures, 2001,38(38):6723-6749.

[9] 路国运,张善元.柱壳轴向冲击屈曲实验研究及其应力波效应的分析[J].太原理工大学学报,2008,39(1):13-16. Lu Guo-yun, Zhang Shan-yuan. Experimental research on dynamic buckling of the cylindrical shell subjected axial impact and the analysis of the stress wave effect[J]. Journal of Taiyuan University of Technology, 2008,39(1):13-16.

[10] Linderberg H E, Herbert R E. Dynamic buckling of a thin cylindrical shell under axial impact[J]. Journal of Applied Mechanics, 1966,33(1):105-112.

[11] Chen D H, Ushijima K. Estimation of the initial peak load for circular tubes subjected to axial impact[J]. Thin-Walled Structures, 2011,49(7):889-898.

[12] 郑波，王安稳.轴向应力波作用下圆柱壳弹性轴对称动力失稳有限元特征值分析[J].力学季刊，2007，27(4):675-680. Zheng Bo, Wang An-wen. Finite element eigenvalue analysis for dynamic buckling of cylindrical shell is under axial elastic compression wave[J]. Chinese Quarterly of Mechanics, 2007,27(4):675-680.

[13] 顾红军，赵国志，陆廷金，等.轴向冲击下薄壁圆柱壳的屈曲行为的实验研究[J].振动与冲击,2004,23(4):58-63. Gu Hong-jun, Zhao Guo-zhi, Lu Ting-jin, et al. Buckling of thin-wall cylindrical shell under axial impact[J]. Journal of Vibration and Shock, 2004,23(4):58-63.

[14] Gordienko B A. Buckling of inelastic cylindrical shells under axial impact[J]. Archives of Mechanics, 1972,24(3):284-294.

[15] 韩铬宝，王仁.圆柱壳轴向塑性动力失稳的第二临界速度[J].强度与环境,1988(4):30-36. Han Ming-bao, Wan Ren. Second critical limit velocity of the dynamic plastic buckling of cylindrical shell[J]. Structure & Environment Engineering, 1988(4):30-36.

[16] Wang Ren. On secondary bifurcation of a slender body[C]∥Sino-Japanese Symp Deformation/Fracture of Solids. Huangshan, China,1997.

[17] 徐新生，苏先樾，王仁.轴向应力波与弹塑性材料圆柱壳的动力屈曲[J].中国科学:A,1995，25(2):166-173. Xu Xin-sheng, Shu Xian-yue, Wang Ren. Axial stress wave and dynamic buckling of the elasto-plastic cylindrical shell[J]. Science in China: A, 1995，25(2):166-173.

[18] Wierzbicki T, Bhat S U, Abramowicz W, et al. Alexander revisited a two folding elements model for progressive crushing of tubes[J]. International Journal of Solids and Structures, 1992,29(24):3269-3288.

[19] 韩志军.直杆的撞击屈曲及其应力波效应的实验和理论研究[D].太原:太原理工大学，2006.

(责任编辑 丁 峰)

Dynamic buckling of the cylindrical shell impacted by large mass with low velocity

Lu Guo-yun, Duan Chen-hao, Lei Jian-ping, Han Zhi-jun, Zhang Shan-yuan

(ShanxiKeyLaboratoryofMaterialStrengthandStructureImpact,TaiyuanUniversityofTechnology,Taiyuan030024,Shanxi,China)

The experimental investigations on dynamic buckling of brass and steel cylindrical shell under axial impact were carried out using drop hammer as loading apparatus. Multiple buckling models are observed and the time histories of impact force were recorded. The experimental results show that the steel cylindrical shell buckled progressively and the brass cylindrical shell occur dynamic plastic buckling (the entire length of a cylindrical shell wrinkles before the development of large radial displacements) when they subjected impact from a mass in relatively low velocity. These results confirm that the dynamic plastic buckling does not necessarily require high impact velocity. This conclusion conflicts with the established perception that the high impact velocity is a necessary condition for dynamic plastic buckling.

solid mechanics; dynamic progressive buckling; drop hammer; cylindrical shell; dynamic plastic buckling

10.11883/1001-1455(2015)02-0171-06

2013-09-05；

2013-12-11

国家自然科学基金项目(11072167,11372209);山西省留学人员科技活动项目(2013-044)

路国运(1973— )，男，教授，luguoyun@tyut.edu.cn。

O342;TU375 国标学科代码： 1301565

A