固体材料高功率激光斜波压缩研究进展*

李 牧,孙承纬,赵剑衡

(中国工程物理研究院流体物理研究所,四川 绵阳 621999)



固体材料高功率激光斜波压缩研究进展*

李 牧,孙承纬,赵剑衡

(中国工程物理研究院流体物理研究所,四川 绵阳 621999)

利用高功率激光诱导的应力波对固体材料进行高应变率斜波压缩，是近年来快速发展的新型动高压实验技术。与传统加载手段不同，它可以在数ns时间内以极高的应变率(106～109s-1)将薄样品平滑加载到数千万大气压，并仍然保持其固体状态。结合多种先进的诊断技术，可以测得样品材料的热力学、动力学参数和原位微观结构特性，是研究动高压物理、物态方程和高应变率动力学问题的先进途径。本文梳理了这种技术的发展历程，对其加载和诊断技术以及已取得的主要结果进行综述，并展望了其发展前景。

爆炸力学；斜波压缩；高功率激光；固体材料；物态方程；应变率相关

高功率激光与凝聚态靶相互作用可以产生极高的烧蚀压力，形成高压冲击波在靶物质中传播，实现对物质的高度压缩[1-2]。与传统冲击加载手段(Hopkinson杆、炸药爆轰、轻气炮等，加载压力100～105MPa，加载应变率103～107s-1)相比，激光驱动冲击加载可实现超高压力(108MPa 或102TPa量级)[3-4]和超高应变率(106～109s-1)[5],并且利用不同的激光脉冲波形和作用方式还可实现多次冲击[6-7]、无冲击[8-13]、三角波[14-16]、等容加热等各种可控加载路径。更重要的是，在进行压缩加载的同时还利用另外的诊断激光束脉冲产生所需要的辐射源(如X射线、质子等)[17-19]，进行样品材料的物理、力学参量和微介观形貌或结构的原位测量与诊断，建立重要的多尺度实验研究体系[20]。

由于上述原因，自20世纪70年代起激光驱动高压的实验途径就引起了关注[1-2,21-23]。继实现TPa量级的冲击压缩之后，R.Cauble等[3]在NOVA装置上用激光驱动高速飞片的方法达到了75 TPa的峰值冲击压力，但此方法由于实验精度不高而没有继续下去，转向数据更可靠的实验途径。

当前用于动高压实验的高功率激光设施有NIF、OMEGA、JANUS、Trident、LULI、HELEN、GEKKO-XII(Firex)、神光II和神光III原型。20世纪70年代以后30年间，激光加载手段主要是烧蚀冲击波直接压缩或激光驱动高速飞片间接碰撞，加载途径、冲击压力和实验精度存在较大局限。事实上，由于制靶、束匀滑、波形调控、预热抑制以及诊断技术等原因，激光冲击实验数据跟其他加载手段实验的结果之间存在一定差别，其中一个重要原因在于激光加载的超高应变率特点。

21世纪以来，各种配套技术不断改进(如冲击波参数测量误差小于2%[24])，支撑了激光驱动技术的创新。主要进展有3个方向：激光驱动准等熵(斜波)压缩[8-13]、透明介质Hugoniot状态的连续测量[14,16,25-31]以及激光辐照受静压样品的动静联合加载实验[32-34]。这些途径都是围绕物态方程展开的。利用准等熵压缩希望得到高压低温的材料状态，对于过渡段物态方程很重要，因为该范围内冲击绝热线(Hugoniot)数据准确度较低，需要由别的数据进行校核。利用激光驱动的衰减冲击波加载，可获得透明介质(尤其氘、氚[34]以及标准材料[14,29,35-38]的完全物态方程数据，依靠先进的连续测量技术能够给出波传播状态拐点的高精度结果，这是以前用多发多点测量实验很难实现的。动静结合实验技术对于气体、液体的高压物态方程研究是革命性进步。传统静高压平台上样品区较大且容器材料强度有限，静压力很难提升至上万大气压。采用激光加载增压，则样品区直径可小于mm尺度，适合使用金刚石压砧，使初始静压力达到5 GPa[32],初始密度有数倍提高，从而可获得多条不同初始密度的Hugoniot线。由于初始密度对冲击绝热线的影响远高于温度和压力，因此这条途径对宽区物态方程研究将发挥重大作用，对天体物理和聚变点火实验有推动作用。本文中仅介绍激光斜波压缩技术[39]和实验的进展。

自然界和工程技术的很多动力学过程及其中物质的热力学状态，往往不是传统冲击动力学加载的单次冲击情形[20,40]，如行星内核的演变不是一个绝热过程，而是介于等熵压缩与等温压缩之间的某种过程，同时还发生多种相变[41]。武器内爆过程中有关材料经过多次冲击、卸载、再加载，更接近于等熵压缩的状态。对于这些需求，通过准等熵压缩实验有望丰富物质热力学状态数据库，拓宽高压物理实验研究的范围。从早期的斜波发生器、爆轰到磁驱动技术，斜波准等熵加载已取得了重大进展，尤其是1999年J.R.Asay在Z机器上创造的磁驱动准等熵压缩实验技术[42]，对激光驱动斜波加载技术产生了很大的影响。J.Edwards等[8]基于爆轰产物空腔驱动的经验，提出了激光烧蚀薄膜靶产生射流进行斜波加载的思路，迅速创造了激光驱动高应变率准等熵加载的实验技术。

1 激光斜波压缩的基本技术途径

图1 激光驱动斜波压缩的基本途径[8,11,43,46]Fig.1 Approaches to ramp compression by laser[8,11,43,46]

自从J.Edwards等[8]开展了激光驱动无冲击压缩实验，D.C.Swift等[43]、N.Amadou等[44]、M.Koenig等[45])相继开展了类似的工作。这种基本途径已经发展了多种类型，其概念和起源见图1。

1.1 加载波形调节技术

图1中途径1是利用波形调节技术[43-45,47]，把时间调制的基频或倍频激光束直接作用到材料样品上，控制激光光强随时间逐渐增大，产生平滑上升的加载压力，实现斜波压缩。途径4也是利用波形经时间调制的激光束，通过黑腔转换为软X射线再辐照样品[41,46,48-49]。近年来很多激光装置的种子源都已经升级为任意波形发生器，并且整个光路放大系统具备了全程光学传递函数的闭环控制，与D.C.Swift等[43]开始的波形调节实验相比有了质的飞跃，便于直接进行途径1和途径4的实验。总的看来，目前的波形调节能力主要受限于激光的总脉宽，大部分装置的最大可调脉宽不超过10 ns，只有在NIF上目前可实现20 ns的脉宽，对于斜波加载实验仍然有些偏短。若要把典型金属样品加载到TPa量级，则终态拉氏声速cL应达到初始声速cL0的8～10倍以上。在足够理想的优化波形情况下，可认为冲击波形成最远位置约等于初始声速cL0与激光脉宽τ的乘积，也就是样品可能的最大厚度。事实上厚度为d的样品中，其粒子速度上升沿的宽度近似等于τ-d/cL0，还必须高于一定的临界值，才能防止冲击波的出现。因此，激光脉宽适当长些是有利的。

为降低辐射热波(包括热电子和X射线)的影响，材料样品层通常需要包覆低原子序数烧蚀层和屏蔽层，从而实际有效的面应力波上升沿更短。但是如果加载脉宽过于增大，烧蚀深度也会加大，又会出现二维效应和不稳定性扰动。这些问题都可能导致实验数据质量下降。

实验设计上为了延长速度剖面的上升沿，需要增大cL0,通常采用一个初始强冲击波最先进入样品，加载路径成为“冲击波”加“斜波”，这种方式实验上比较容易实现。引入初始强冲击还有另外一个优点，就是使材料适当热软化[41]，从而在后期斜波压缩过程中可以忽略应力偏量的影响，直接给出流体静水压力与比容的关系，这对物态方程研究是有利的。从2009年开始，在OMEGA装置上开展了多发次的冲击-斜波实验[20]。在NIF上则在2011年开始利用20 ns的加载波形进行冲击-斜波实验，近年来仅以每年十几发的实验量，就取得了斜波压缩实验一系列的新进展[39,50-51]。

关于NIF上波形优化的工作还没有系统的文献报道，仅见到D.C.Swift等[52]的一篇文章，Jin Yun-sheng等[53]、Xue Quan-xi等[47,54]、Shu Hua等[55]也在这方面做了研究，并初步开展了实验验证。

1.2 气库膜结构

图1中途径2是使激光束直接作用于塑料薄膜(气库膜)并产生烧蚀冲击波[8,10,13,56-64]，当该波透出薄膜后表面时烧蚀等离子体发生强卸载，形成高速、高密度梯度的自由射流，通过一段空腔距离后形成具有所需动量分布的加载射流，再撞击压缩材料样品。途径3与途径2类似，不同的是激光束进入黑腔，通过辐照高原子序数黑腔材料，产生软X射线再辐照气库膜，这种方法能产生强度更高、更接近平面一维的加载射流源[11-12,59]。采用这2种途径可通过对气库膜的处理基本消除样品预热，其加载波上升时间也可通过实验靶参数的设计进行较大范围的调整(数ns到几十ns)，其加载波的平面性以及实验测量精度都能满足材料动态响应和物态方程数据的需要，并可降低对激光装置波形调节能力的要求。

Li Mu等[9]对激光直接烧蚀气库膜进行准等熵压缩实验的多个影响参数进行了系统的数值分析，包括激光脉宽、波长、功率密度、能量密度、气库膜厚度、空腔厚度、样品阻抗等。合理设计的黑腔驱动途径能够产生平面性更好的结果，但在腔内产生的硬X射线和激光一次反射引起的超热电子都会造成样品的预热，为此R.F.Smith等[11-12]主要采用黑腔与掺溴气库膜的方法。受掺溴技术的限制，李牧等采用金属夹层气库膜的结构，达到了预期的屏蔽效果，同时还拉长了加载应力的上升沿。这种多层气库膜技术类似传统的阻抗调节技术[58]，可以在不改变入射激光的条件下优化斜波加载的应力波形。从渗透技术、三维加工、多层膜到NIF上使用的更复杂的靶结构[58-59,65]，主要目的是拉长加载上升沿时间，提高斜波加载峰值压力。NIF上近期的实验表明，这种创新有望实现接近TPa量级峰值压力的长脉宽斜波压缩，对于重金属材料的准等熵压缩具有重要意义。虽然气库膜本身的烧蚀吸收能量，导致压缩效率大大降低，但却可以很好地控制辐射预热，而且射流撞击样品所引起热波的传播速度远低于应力波，所以加载环境很干净，加载脉宽又很长，有利于在不宜进行波形调控的激光装置上开展斜波压缩实验。从这些分析来看，气库膜技术是一种适应性较强的接近简单力学加载的斜波实验技术。

2 激光斜波压缩数据的实验测量

2.1 材料样品表面速度和温度的测量

激光斜波压缩实验的测量诊断同样需要以波剖面测量为基础。由于有效过程仅有几十ns，而且样品尺寸很小，无法排布多个探头，条纹相机记录的线成像VISAR就成了最重要的测量工具[27]，可以同时记录下多个台阶厚度样品的表面或界面速度历史，还可以给出加载平面性和界面反射率的信息。基于VISAR反射率[14,28]的主动测量，目前已经成为一个反算样品表面温度的重要手段，在物态方程研究中发挥了重要作用，尤其是在低温段比被动SOP(条纹相机记录的光学高温计)技术的精度高得多[30]。根据不同厚度样品的表面/界面速度历史，考虑阻抗匹配修正后可以算出设想的半无限厚样品中相应于实际样品厚度处的原位粒子速度，从而得出拉氏声速，即可算出应力-比容关系(准等熵压缩线)[40]。这是准等熵压缩实验典型的测量数据处理方法，其中最关键的是获得精确的原位粒子速度。跟磁驱动实验一样，这种处理方法获得的准等熵压缩线包含了应力偏量，需要再处理才能得到静水压力表征的物态方程数据，但目前还没有发现更合适的办法[66-68]。

2.2 X射线衍射(XRD)诊断技术

很多实验无法获得多个厚度处样品的粒子速度，譬如上面提及的波形调节能力受到上升沿宽度限制的情形，又如高压力下厚样品中无法避免形成冲击间断。为了取得更多的新数据，D.H.Kalantar等[18,69，71-72]、A.Loveridge-Smith等[70]、J.Hawreliak等[73]、J.A.Hawreliak等[74]探索了激光诱导的X射线衍射测量技术，一部分光束进行加载，另一部分光束聚焦轰击单质靶作为单能、微焦点X射线源，通过精确地同步控制，对斜波加载的样品结构和参数进行瞬态精密诊断。例如通过衍射技术可以获得比容数据，但如何同时确定样品中的压力？使用透明的标准材料作为窗口，有望解决这个重要问题。

进行X射线的衍射或谱测量(包括XRD、EXAFS等技术)，最关键的是探针光的选取和光源的优化[75]。为进一步提高He-α线的对比度并降低高能辐射背景，J.H.Eggert[39,51]、A.Higginbotham等[76]已做了很多优化工作，这是提高衍射或谱数据精度的重要内容，值得关注。

2.3 标准窗口材料研究

M.D.Knudson等[36,38，77]在ZR机器上利用准等熵发射的超高速铝、铜飞片进行了上百发实验，标定了z-切割α石英材料的高压冲击绝热线。D.G.Hicks等[29,78]在OMEGA激光器上先以铝为标准材料，用阻抗匹配法确定了z-切割α石英在0.2～1.5 TPa的高精度冲击绝热线(冲击波速度测量误差小于2%)，然后再以石英作为参考，得到纳米晶金刚石在0.6～1.9 TPa范围的结果，冲击波速度和密度的测量误差分别为(0.3～1.1)%和(0.2～2.7)%，达到了作为标准材料的要求。R.F.Smith等[41]、D.K.Bradley等[46]开展人造金刚石斜波压缩实验的主要目的是获得其准等熵压缩线，结合冲击压缩线数据建立金刚石作为与重金属阻抗匹配的超高压窗口材料的数据库。为获得更高精度的数据，单晶金刚石材料的标定还在进行中。

选择金刚石作为标准窗口材料主要有2个考虑：其一是阻抗高(主要由于声速高)，与待测的几种重金属材料的阻抗相差不大；其二是碳单质，对硬X射线的吸收非常弱，是理想的X射线窗口材料。

2.4 夹层薄膜材料样品结构

图2是在NIF上正在进行的钽的高压物态方程测量方案(TARDIS，tardet diffraction in situ)和实验靶[51]，采用平面夹层靶设计，用VISAR记录人造金刚石(HDC)砧靶的自由面速度历史，锆膜产生的He-α线作为探测(探针)束，衍射方案为粉末衍射。注意到夹层靶中被测钽样品的厚度仅5 μm，两侧均为高密度碳(人造金刚石)，激光烧蚀左侧金刚石产生的应力波向右传播，应力波在钽两侧金刚石砧靶表面的来回反射，其渡越时间相对于整个加载脉宽可以忽略，即钽样品的厚度为流体力学薄[75]。从而可认为钽层内部压力基本一致，并等于金刚石窗口加载面上的压力。这样，通过金刚石窗口自由面速度反演到加载面即可获得样品的实时压力历史，并可与衍射获得的比容结果对照。这就是NIF上开展超高压力范围斜波压缩物态方程测量的主要思路。

图2 NIF正在进行的钽样品高压斜波压缩测量方案和实验靶[51]Fig.2 Sketch map of target diffraction in situ (TARDIS) and C-Ta-C sandwich target utilized by NIF[51]

2.5 扩展吸收边精细谱结构(EXAFS)诊断技术

除衍射测量，利用扩展吸收边精细谱结构的诊断也是物态方程研究的一个重要途径[60,79-85]。这种方法的基本原理是:原子中内层电子的跃迁过程会受到与临近电子云有交叠的原子的影响，导致吸收谱线在K壳层吸收边前后发生波动，产生精细结构。由于不同原子的K吸收边相差很远，这种技术能够直接测量指定元素的微观结构、密度和温度，提供与压力相关联的数据。这类实验需要高亮度的X光白光光源，在大型激光装置上可通过专门设计的靶丸内爆实现，一般要求这种源光谱在被测样品吸收边附近具有连续光滑的谱分布，这样才能获得高信噪比的吸收谱原始信号。信噪比是实验成功与否的核心，因为透射测量吸收边外高能区信号已很弱，加载激光与靶相互作用也会产生X射线干扰，因此必须使探针光的亮度远高于此。目前利用这种技术主要在OMEGA上开展实验，NIF上暂时还没有看到这方面的结果，EXAFS数据和XRD数据可相互参考，对于完全物态方程数据的获取大有裨益。

3 激光驱动斜波压缩物理研究的进展

3.1 高压范围的多相物态方程

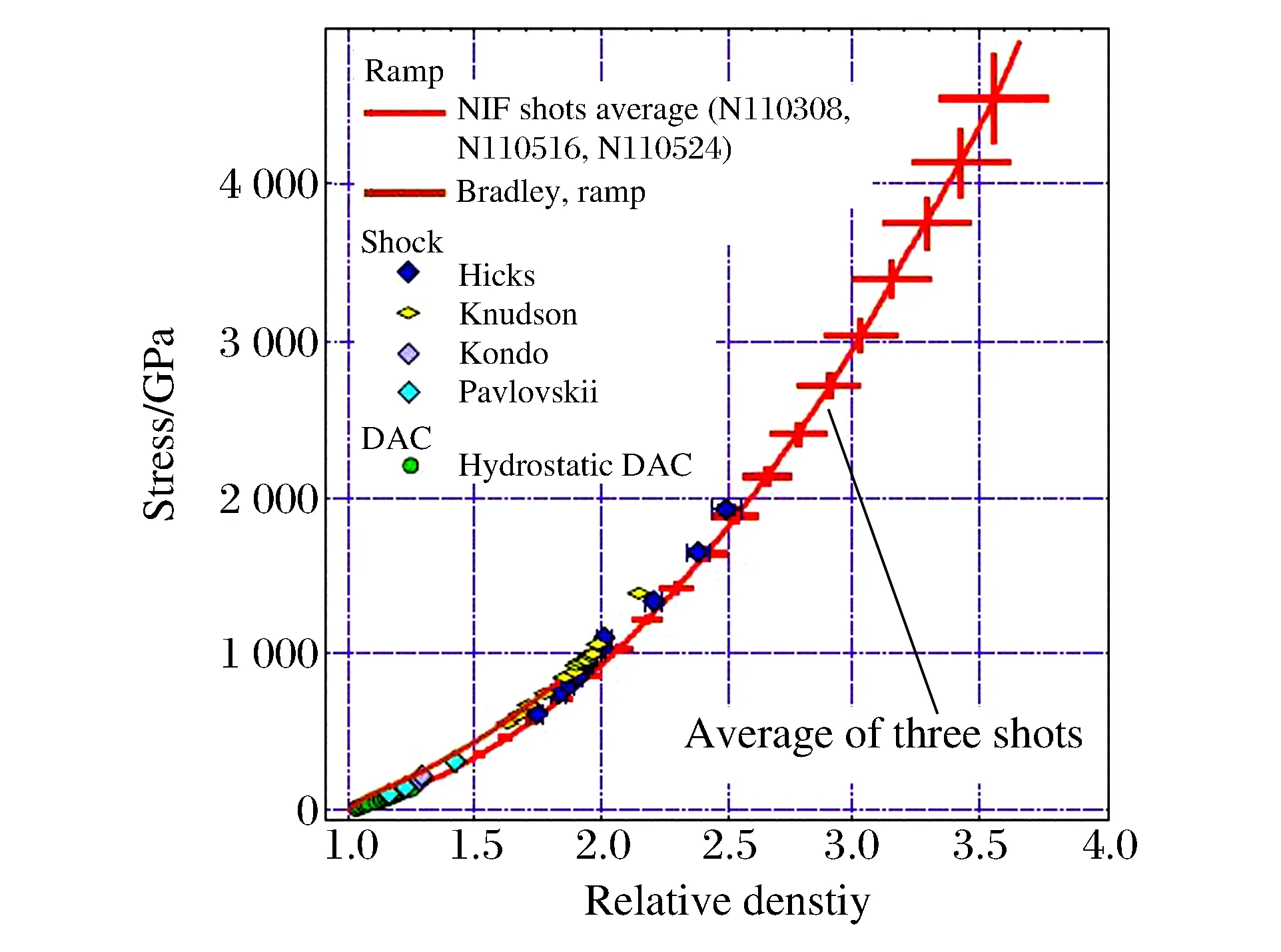
图3 金刚石在无冲击加载和冲击-斜波加载下的不同响应曲线[39]Fig.3 Different stress-density curves of diamond under shockless or shock-ramp loading[39]

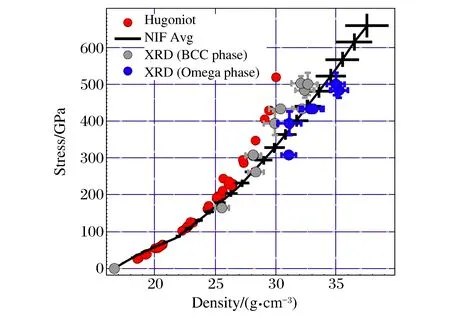
图4 600 GPa以下钽的物态方程测量结果，冲击-斜波加载声速测量和衍射测量的对比[50]Fig.4 Stress-density relations in 600 GPa, shock or ramp compression, there is different between results from sound and diffraction measurement[50]

物态方程研究是开展准等熵压缩实验的主要目的，尤其是重金属物态方程在核武器物理研究中意义重大。如前所述，斜波压缩实验研究的目的是得到材料TPa量级高压下的固态参考点，而在200～500 GPa以下的静高压和冲击绝热线的精度已满足要求，而且热力学准等熵线与冲击绝热线的差别不大。10年来，大部分斜波压缩实验的加载范围都在200～500 GPa以下，为了追求更接近理论等熵线的结果，包括磁驱动和激光驱动技术都重点发展无冲击的纯斜波加载方式，但得到的实验数据都比理论等熵线偏硬。分析发现在高应变率加载下声子阻尼造成材料屈服强度和流动应力大幅增长，这个现象在激光驱动中尤其明显[55,62-63,86-88]。虽然这个现象反映了材料的应变率响应特性，但给物态方程的精密研究造成很大麻烦，因为应力偏量与主应力的比值明显超过物态方程许可的误差范围。扣除应力偏量的准等熵线可以称为表观等熵线，虽然仍然包含各类耗散引起的附加热压，但已可作为热力学物态方程的参考线。困难是如何确定应扣除的应力偏量值，这个问题可能在短期内不容易解决。

好在最关心的是百GPa及更高压力范围的物态方程，通过引入初始强冲击波，让材料热软化，进入可以忽略强度的准流体状态[41]，然后再进行斜波压缩。采用这种方式可以显著降低斜波压缩过程中的热耗散，提高压缩比。图3给出了一个典型的例子，左下角0～800 GPa的线是用无冲击加载方式获得的，0～5 TPa的线是用冲击-斜波加载方式获得的，初始冲击波的强度约为110 GPa，实际上是金刚石的Hugoniot弹性极限。在这种状态下，初始冲击应变并没有包含产生加工硬化的塑性应变，是一种低熵增途径。与此同时，人造金刚石中烧结留下的初始空隙完全闭合，后期斜波作用过程中均可视为密实材料。图3的2条准等熵线都是用多台阶自由面速度剖面计算给出的，明显看出无冲击加载结果比冲击-斜波加载结果偏硬很多。NIF的结果在1 TPa以下几乎和冷压线重合，偏应力的份额很小，可认为总应力和静水压相当，可以作为物态方程的等熵参考线。

NIF和OMEGA上的实验都没有观察到明显的相变信号，而在冲击相变实验中可明显观察到，这可能与金刚石相到BC8相的相变速率过慢有关，NIF斜波加载的应变率太高，这方面的证据还需补充。

由于金刚石是自然界最硬的材料，初始声速极高，因此适合采用粒子速度和声速测量的方法来获得响应曲线，其价值在于作为衍射和吸收谱测量中的高压物态方程标准材料。图4给出了重金属钽在600 GPa范围内物态方程的等熵线数据[50]，其中的准等熵线是基于冲击-斜波加载多台阶靶声速测量获得的，可以看出在200 GPa以上与Hugoniot线的差别很明显。以bcc结构进行分析给出的300 GPa以下的衍射测量结果与声速测量结果吻合良好，但300 GPa以上则出现明显分歧，显示hcp相给出的比容更接近声速测量结果，预示发生晶体结构相变的可能性极大。在类似实验中也发现铅在700 GPa的斜波压缩下也从bcc相转变成hcp相。通过衍射实验还观察到了锡冲击熔化后继续进行斜波压缩时重新发生了重结晶过程。利用夹层靶结构的衍射实验，F.Coppari等还发现了MgO在斜波加载到600 GPa时发生了结构相变[89]，从NaCl型的B1结构转变成CsCl型的B2结构，一直到900 GPa都保持稳定。这是首次从实验上观测到相变证据，之前的冲击实验中MgO进入该压力区域都发生了融化。Y.Ping等[79]基于多冲击-斜波加载，用EXAFS方法对铁高压相图进行了新的探索，发现一直到560 GPa前铁样品都维持稳定的hcp相，同时对铁高压段的融化边界进行了限定。

3.2 低压范围材料动力学应变率响应特性研究

在较低的压力范围内，激光驱动的高应变率特性便于进行高应变率加载下的材料动力学特性研究，在这之前要达到107s-1以上的应变率几乎是不可能的。冲击加载实验中应变率无法解耦，静压加载时应变率接近零，其他动压加载能达到的应变率较低。

材料的弹塑性转变对晶粒尺度及样品尺度、温度、应变率、晶向(单晶)、初始缺陷密度等参数比较敏感，是材料动力学研究的重要内容。利用激光斜波加载，对多种材料的弹塑性转变已进行了实验研究，图5给出了铝、硅、铁、钽4种材料的动态弹性极限随应变率的变化关系。

图5(a) 铝[88]的Hugoniot弹性极限与应变率的关系
Fig.5(a) Elastic limit as a function of strain rate for Al[88]

图5(b) 硅[92]的Hugoniot弹性极限与应变率的关系
Fig.5(b) Elastic limit as a function of strain rate for Si[92]

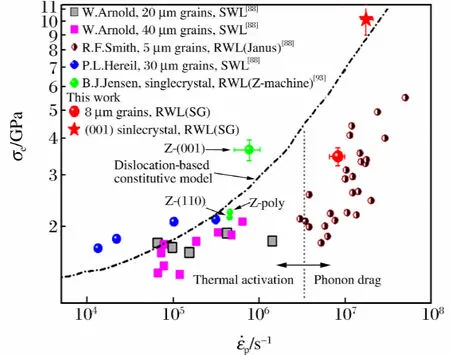
图5(c) 铁的Hugoniot弹性极限与应变率的关系
Fig.5(c) Elastic limit as a function of strain rate for Fe

图5(d) 钽[20]的Hugoniot弹性极限与应变率的关系
Fig.5(d) Elastic limit as a function of strain rate for Ta[20]

由图5可明显看出：在高于107s-1的应变率范围内，这些材料的弹性极限出现大幅增长。文献中大多将其解释为：由于声子拖曳机制，位错传播速度受到声子散射的阻滞，因而屈服强度增大。判断控制机制是否为声子拖曳的一个简单方法是改变材料温度。注意到声子阻尼随温度的升高而升高，但是低应变率实验中材料屈服强度随温度升高而下降，表明非声子拖曳作用。若出现强度随温度升高而增大的相反现象，则可能是声子拖曳在起作用。Shu Hua等[55]在激光驱动实验中得到的铝样品Hugoniot弹性极限数据佐证了这个作用。低应变率加载下塑性屈服主要通过热激活机制，位错依靠晶格的热振动突破势垒，因而温度越高位错越容易激活，而且位错移动速度随剪切应力增大呈指数上升。在声子拖曳机制下，位错速度随剪切应力增大呈线性上升。

相转变起始压力的数据也呈现类似规律，如图6所示。激光加载的斜波实验给出铁α-ε相变的起始压力达到15～20 GPa，在更高应变率的实验中R.Smith竟然认为相变起始点达到了38 GPa，他判断相变开始的依据是拉氏声速曲率的变化，这可能与一级相变的物理特性有所差别。Li Mu等开展的单晶铁和多晶铁样品的激光无冲击实验表明，除弹性极限差别较大，多晶铁和单晶铁在相转变压力上几乎一致；同时开展的大角度衍射实验结果表明，斜波加载下相变动力学过程与冲击加载相比明显不同，冲击加载下新相畴的形成仅需几十ps[90]，斜波加载下单晶样品经历较长时间的塑性变形后到达相变压力状态，此时实际上已经不是单晶体了，而且用单晶诊断方法也没有获得新相的衍射峰。

高应变率斜波加载下铋的I-II相变边界出现了明显的滞后[64]，即非平衡边界向高压方向偏移。Yu Ji-dong等[91]利用相场方法对该过程进行了模拟分析，所得结果与实验结果吻合很好，这有助于深入理解相变动力学。

斜波压缩实验还为高压下固体材料强度的研究创造了可能。激光加载下的斜波压缩要取得完整的加载、卸载曲线通常比较困难，因此激光加载下用双屈服面方法进行强度研究，可能存在预热的影响。相对来讲，利用RT不稳定增长因子法和纵波震荡法测量材料强度也不失为有效的手段。RT不稳定增长因子法已经在OMEGA和NIF上分别开展了对钒和钽实验，这类实验不但能够提供强度的信息，也为构型实验奠定了基础，一举两得。

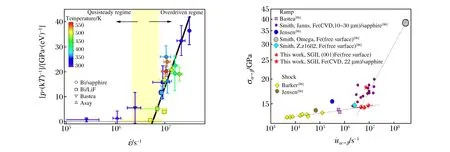
图6 材料结构相变的驱动压力与加载应变率的关系，铋[64]、铁Fig.6 Over-driven pressure as a function of strain rate for Bi[64] and Fe

4 总结与展望

除准等熵压缩的一般特点，激光斜波加载的特色和研究意义还有以下几点：

(1)加载压力峰值最高。目前NIF上得到的最高斜波压力峰值已达到7 TPa，首先实现了从常压到TPa压力的单轴应变斜波方式的持续压缩，其他技术途径短期内无法达到。

(2)加载应变率最高。激光驱动斜波加载能够在ns量级时间内使材料从常压进入TPa压力状态，加载应变率峰值可以达到106～109s-1，比磁驱动途径高约2个量级。

(3)加载路径灵活可控。通过对激光波形、功率密度等参数以及气库膜和射流飞行距离(真空腔)的优化设计，可实现样品加、卸载参数、路径可控，获得更丰富的材料偏离Hugoniot状态的热力学信息。

(4)可以同时进行多项原位诊断实验。与宏观力学参量实时测量的同时，利用高同步精度的各项原位诊断实验可以获得样品材料的丰富微、介观信息，了解其高压晶相结构，得到更直接的物态方程数据，开展相变动力学研究。由于激光加载能够达到更高更宽的状态区域，激光原位诊断实验对于动高压物理的意义，将远超过同步辐射诊断之于静高压实验。

激光驱动准等熵压缩实验已从技术探索发展到可为核武库维护提供高精度数据的程度，超高压斜波物态方程数据已经成为NIF设施(也是磁驱动ZR机器)的主要物理进展之一，其进展速度之快超乎想象。激光加载和诊断技术不断丰富，研究目标和框架已基本清晰，除数据精度和质量有待进一步提高外，原来认为极其复杂的数据处理问题已合理简化，然而高压物理本身却面临着新的挑战—超高压和超高应变率加载下材料的超固态结构及其变化机制有待于深入研究。

[1] Van Kessel C G M, Sigel R. Observation of laser-driven shock waves in solid hydrogen[J]. Physical Review Letters, 1974,33(17):1020-1023.

[2] Salzmann D, Eliezer S, Krumbein A D, et al. Laser-driven shock-wave propagation in pure and layered targets[J]. Physical Review A, 1983,28(3):1738-1751.

[3] Cauble R, Phillion D W, Hooveret T J, et al. Demonstration of 0.75 Gbar planar shocks in x-ray driven colliding foils[J]. Physical Review Letters, 1993,70(14):2102-2105.

[4] Swift D, Hawreliak J, Braun D, et al. Gigabar material properties experiments on NIF and Omega[C]∥Elert M L, Buttler W T, Borg J P, et al. Shock Compression of Condensed Matter-2011: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter. Chicago: the American Physical Society, 2011.

[5] Lindl J D, Amendt P, Berger R L, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility[J]. Physics of Plasmas, 2004,11(2):339.

[6] Munro D H, Celliers P M, Collins G W, et al. Shock timing technique for the National Ignition Facility[J]. Physics of Plasmas, 2001,8(5):2245.

[7] Shigemori K, Shimizu K, Nakamoto Y, et al. Multiple shock compression of diamond foils with a shaped laser pulse over 1 TPa[J]. Journal of Physics: Conference Series, 2008,112(4):042023.

[8] Edwards J, Lorenz K T, Remington B A, et al. Laser-driven plasma loader for shockless compression and acceleration of samples in the solid state[J]. Physical Review Letters, 2004,92(7):075002.

[9] Li Mu, Zhang Hong-ping, Sun Cheng-wei, et al. Numerical analysis of laser-driven reservoir dynamics for shockless loading[J]. Journal of Applied Physics, 2011,109(9):093525.

[10] Hawreliak J, Colvin J, Eggert J, et al. Modeling planetary interiors in laser based experiments using shockless compression[J]. Astrophysics and Space Science, 2007,307(1/2/3):285-289.

[11] Smith R F, Eggert J H, Jankowski A, et al. Stiff response of aluminum under ultrafast shockless compression to 110 GPa[J]. Physical Review Letters, 2007,98(6):065701.

[12] Smith R F, Pollaine S M, Moon S J, et al. High planarity x-ray drive for ultrafast shockless-compression experiments[J]. Physics of Plasmas, 2007,14(5):057105.

[13] Miyanishi K, Ozaki N, Brambrink E, et al. Characterization of laser-driven ultrafast shockless compression using gold targets[J]. Journal of Applied Physics, 2014,116(4):043521 [14] Eggert J H, Hicks D G, Celliers P M, et al. Melting temperature of diamond at ultrahigh pressure[J]. Nature Physics, 2010,6(1):40-43.

[15] Spaulding D K, McWilliams R S, Jeanloz R, et al. Evidence for a phase transition in silicate melt at extreme pressure and temperature conditions[J]. Physical Review Letter, 2012,108(6):065701.

[16] McWilliams R S, Spaulding D K, Eggert J H, et al., Phase transformations and metallization of magnesium oxide at high pressure and temperature[J]. Science, 2012,338(6112):1330-1333.

[17] Luo S N, Swift D C, Tierney T E, et al. Laser-induced shock waves in condensed matter: Some techniques and applications[J]. High Pressure Research, 2004,24(4):409-422.

[18] Kalantar D H, Belak J F, Collins G W, et al. Direct observation of the α-ε transition in shock-compressed iron via nanosecond x-ray diffraction[J]. Physical Review Letters, 2005,95(7):075502.

[19] Gotchev O V, Chang P Y, Knauer J P, et al. Laser-driven magnetic-flux compression in high-energy-density plasmas[J]. Physical Review Letter, 2009,103(21):215004.

[20] Collins G. Physics of dense matter[C]∥Proceedings of the 2013 HEDP Summer School. Ohio State University, 2013.

[21] Benuzzi A, Löwer T, Koenig M, et al. Indirect and direct laser driven shock waves and applications to copper equation of state measurements in the 10-40 Mbar pressure range[J]. Physical Review E, 1996,54(2):2162-2165.

[22] Cottet F, Romain J P, Fabbro R, et al. Ultrahigh-pressure laser-driven shock-wave experiments at 0.26 μm wavelength[J]. Physical Review Letters, 1984,52(21):1884-1886.

[23] Trainor R J, Holmes N C, Anderson R A, et al. Shock wave pressure enhancement using short wavelength (0.35 μm) laser irradiation[J]. Applied Physics Letters, 1983,43(6):542-544.

[24] Fu Si-zu, Huang Xiu-guang, Ma Min-xun, et al. Analysis of measurement error in the experiment of laser equation of state with impedance-match way and the Hugoniot data of Cu up to ～2.24 TPa with high precision[J]. Journal of Applied Physics, 2007,101(4):043517.

[25] Celliers P M, Collins G W, Silva L B D, et al. Accurate measurement of laser-driven shock trajectories with velocity interferometry[J]. Applied Physics Letters, 1998,73(10):1320.

[26] Bradley D K, Eggert J H, Hicks D G, et al. Shock compressing diamond to a conducting fluid[J]. Physical Review Letters, 2004,93(19):195506.

[27] Celliers P M, Bradley D K, Collins G W, et al. Line-imaging velocimeter for shock diagnostics at the OMEGA laser facility[J]. Review of Scientific Instruments, 2004,75(11):4916.

[28] Celliers P M, Collins G W, Hicks D G, et al. Electronic conduction in shock-compressed water[J]. Physics of Plasmas, 2004,11(8):41-44.

[29] Hicks D G, Boehly T R, Celliers P M, et al. Shock compression of quartz in the high-pressure fluid regime[J]. Physics of Plasmas, 2005,12(8):082702.

[30] Miller J E, Boehly T R, Melchior A, et al. Streaked optical pyrometer system for laser-driven shock-wave experiments on OMEGA[J]. Review of Scientific Instruments, 2007,78(3):034903.

[31] Hicks D G, Boehly T R, Celliers P M, et al. Laser-driven single shock compression of fluid deuterium from 45 to 220 GPa[J]. Physical Review B, 2009,79(1):014112.

[32] Jeanloz R, Celliers P M, Collins G W, et al. Achieving high-density states through shock-wave loading of precompressed samples[J]. Proceedings of the National Academy of Sciences, 2007,104(22):9172-9177.

[33] Eggert J, Brygoo S, Loubeyre P, et al. Hugoniot data for helium in the ionization regime[J]. Physical Review Letters, 2008,100(12):124503.

[34] Loubeyre P, Brygoo S, Eggert J, et al. Extended data set for the equation of state of warm dense hydrogen isotopes[J]. Physical Review B, 2012,86(14):144115.

[35] Brygoo S, Henry E, Loubeyre P, et al. Laser-shock compression of diamond and evidence of a negative-slopemelting curve[J]. Nature Materials, 2007,6(4)：274-281.

[36] Knudson M D, Desjarlais M P. Adiabatic release measurements in α-quartz between 300 and 1200 GPa: Characterization of α-quartz as a shock standard in the multimegabar regime[J]. Physical Review B, 2013,88(18):184107.

[37] Ozaki N, Sano T, Ikoma M, et al. Shock Hugoniot and temperature data for polystyrene obtained with quartz standard[J]. Physics of Plasmas, 2009,16(6):062702.

[38] Knudson M D, Desjarlais M P. Shock compression of quartz to 1.6 TPa: Redefining a pressure standard[J]. Physical Review Letters, 2009,103(22):225501.

[39] Eggert J H. Materials at extreme compression[R]. Report No. LLNL-CONF-655773, 2014.

[40] 孙承纬,赵剑衡,王桂吉,等.磁驱动准等熵平面压缩和超高速飞片发射实验技术原理、装置及应用[J].力学进展,2012,42(2):206-218. Sun Cheng-wei, Zhao Jian-heng, Wang Gui-ji, et al. Progress in magentic loading techniques for isentropic compression experiments and ultra-high velocity flyer launching[J]. Advances in Mechanics, 2012,42(2):206-218.[41] Smith R F, Eggert J H, Jeanloz R, et al. Ramp compression of diamond to five terapascals[J]. Nature, 2014,511(7509):330-333.

[42] Cauble R, Reisman D B, Asay J R, et al. Isentropic compression experiments to 1 Mbar using magnetic pressure[J]. Joural of Physics: Condensed Matter, 2002,14:10821-10824.

[43] Swift D C, Johnson R P. Quasi-isentropic compression by ablative laser loading: Response of materials to dynamic loading on nanosecond time scales[J]. Physical Review, 2005,71(6):066401.

[44] Amadou N, Brambrink E, Benuzzi-Mounaix A N, et al. Direct laser-driven ramp compression studies of iron: A first step toward the reproduction of planetary core conditions[J]. High Energy Density Physics, 2013,9(2):243-246.

[45] Koenig M, Benuzzi-Mounaix A, Brambrink E, et al. Simulating earth core using high energy lasers[J]. High Energy Density Physics, 2000,6(2):210-214.

[46] Bradley D K, Eggert J H, Smith R F, et al. Diamond at 800 GPa[J]. Physical Review Letters, 2009,102(7):075503.

[47] Xue Quan-xi, Wang Zhe-bin, Jiang Shao-en, et al. Laser-direct-driven quasi-isentropic experiments on aluminum[J]. Physics of Plasmas, 2014,21(7):072709.

[48] Wang J, Smith R F, Eggert J H, et al. Ramp compression of iron to 273 GPa[J]. Journal of Applied Physics, 2013,114(2):023513.

[49] Wang J, Smith R F, Coppari F, et al. Ramp compression of magnesium oxide to 234 GPa[J]. Journal of Physics: Conference Series, 2014,500(6):062002.

[50] Eggert J. Ramp-compression experiments on tantalum at the NIF and Omega lasers[R]. Report Number: LLNL-CONF-490363, 2011.

[51] Eggert J. Overview of NIF TARDIS shots[R]. Report Number: LLNL-CONF-653683, 2014.

[52] Swift D C, Kraus R G, Loomis E N, et al. Shock formation and the ideal shape of ramp compression waves[J]. Physical Review E, 2008,78:066115.

[53] Jin Yun-sheng, Sun Cheng-wei, Zhao Jian-heng, et al. Optimization of loading pressure waveforms for piston driven isentropic compression[J]. Journal of Applied Physics, 2014,115(24):243506.

[54] Xue Quan-xi, Wang Zhe-bin, Jiang Shao-en, et al. Characteristic method for isentropic compression simulation[J]. AIP Advances, 2014,4(5):057127.

[55] Shu Hua, Fu Si-zu, Huang Xiu-guang, et al. Plastic behavior of aluminum in high strain rate regime[J]. Journal of Applied Physics, 2014,116(3):033506.

[56] Lorenz K T, Edwards M J, Glendinning S G, et al. Accessing ultrahigh-pressure, quasi-isentropic states of matter[J]. Physics of Plasmas, 2005,12(5):056309.

[57] Lorenz K T, Edwards M J, Jankowski A F, et al. High pressure, quasi-isentropic compression experiments on the Omega laser[J]. High Energy Density Physics, 2006,2(3/4):113-125.

[58] Smith R F, Lorenz K T, Ho D, et al. Graded-density reservoirs for accessing high stress low temperature material states[J]. Astrophysics and Space Science, 2007,307(1/2/3):269-272.

[59] Park H, Remington B A, Braun D, et al. Quasi-isentropic material property studies at extreme pressures: From Omega to NIF[J]. Journal of Physics: Conference Series, 2008,112(4):042024.

[60] Yaakobi B, Boehly T R, Sangster T C, et al. Extended x-ray absorption fine structure measurements of quasi-isentropically compressed vanadium targets on the OMEGA laser[J]. Physics of Plasmas, 2008,15(6):062703.

[61] Swift D C, Hawreliak J, El-Dasher B, et al. Flow stress of V, Mo, Ta, and W on nanosecond time scales[C]∥Elert M, Furnish M D, Anderson W W, et al. Shock Compression of Condensed Matter 2009: Proceedings of the American Physical Society Topical Group on Shock Compression of Condensed Matter. Nashville (Tennessee): the American Physical Society, 2009.

[62] Park H S, Remington B A, Becker R C, et al. Viscous Rayleigh-Taylor instability experiments at high pressure and strain rate[J]. Physical Review Letters, 2010,104(13):135504.

[63] Park H S, Remington B A, Becker R C, et al. Strong stabilization of the Rayleigh-Taylor instability by material strength at megabar pressures[J]. Physics of Plasmas, 2010,17(5):056314-9.

[64] Smith R F, Eggert J H, Saculla M D, et al. Ultrafast dynamic compression technique to study the kinetics of phase transformations in bismuth[J]. Physical Review Letters, 2008,101(6):065701.

[65] Prisbrey S T, Park H S, Remington B A, et al. Tailored ramp-loading via shock release of stepped-density reservoirs[J]. Physics of Plasmas, 2012,19(5):056311.

[66] Brown J L, Alexander C S, Asay J R, et al. Extracting strength from high pressure ramp-release experiments[J]. Journal of Applied Physics, 2013,114(22):223518.

[67] Brown J L, Alexander C S, Asay J R, et al. Flow strength of tantalum under ramp compression to 250 GPa[J]. Journal of Applied Physics, 2014,115(4):043530.

[68] Vogler T J, Ao T, Asay J R. High-pressure strength of aluminum under quasi-isentropic loading[J]. International Journal of Plasticity, 2009,25(4):671-694.

[69] Kalantar D H, Chandler E A, Colvin J D, et al. Transient x-ray diffraction used to diagnose shock compressed Si crystals on the Nova laser[J]. Review of Scientific Instruments, 1999,70(1):629-632.

[70] Loveridge-Smith A, Allen A, Belak J, et al. Anomalous elastic response of silicon to uniaxial shock compression on nanosecond time scales[J]. Physical Review Letters, 2001,86(11):2349-2352.

[71] Kalantar D H, Allen A M, Gregori F, et al. Laser driven high pressure, high strain-rate materials experiments[C]∥AIP Conference Proceedings: Shock Compression of Condensed Matter. Atlanta: the American Physical Society, 2002,620(1):615-618.

[72] Kalantar D H, Belak J, Bringa E, et al. High-pressure, high-strain-rate lattice response of shocked materials[J]. Physics of Plasmas, 2003,10(5):1569-1576.

[73] Hawreliak J, Colvin J D, Eggert J H, et al. Analysis of the x-ray diffraction signal for the α-ε transition in shock-compressed iron: Simulation and experiment[J]. Physical Review B, 2006,74(18):184107.

[74] Hawreliak J A, Kalantar D H, Stölken J S, et al. High-pressure nanocrystalline structure of a shock-compressed single crystal of iron[J]. Physical Review B, 2008,78(22):220101.

[75] Rygg J R, Eggert J H, Lazicki A E, et al. Powder diffraction from solids in the terapascal regime[J]. Review of Scientific Instruments, 2012,83(11):113904.

[76] Higginbotham A, Patel S, Hawreliak J A, et al. Single photon energy dispersive x-ray diffraction[J]. Review of Scientific Instruments, 2014,85(3):033906.

[77] Knudson M D, Desjarlais M P, Dolan D H. Shock-wave exploration of the high-pressure phases of carbon[J]. Science, 2008,322(19):1822.

[78] Hicks D G, Boehly T R, Celliers P M, et al. High-precision measurements of the diamond Hugoniot in and above the melt region[J]. Physical Review B, 200,78(17):174102.

[79] Ping Y, Coppari F, Hicks D G, et al. Solid iron compressed up to 560 GPa[J]. Physical Review Letters, 2013,111(6):065501.

[80] Mallozzi P J, Schwerzel R E, Epstein H M, et al. Fast extended-x-ray-absorption-fine-structure spectroscopy with a laser-produced x-ray pulse[J]. Physical Review A, 1981,23(2):824-828.

[81] Meyerhofer D D, Yaakobi B, Marshall F J, et al. EXAFS detection of laser shock heating[J]. Bulletin of the American Physical Society (USA), 2001,46(8):294.

[82] Yaakobi B, Marshall F J, Boehly T R, et al. Extended x-ray absorption fine-structure experiments with a laser-imploded target as a radiation source[J]. Journal of the Optical Society of America: B, 2003,20(1):238-245.

[83] Yaakobi B, Meyerhofer D D, Boehly T R, et al. Extended x-ray absorption fine structure measurements of laser shocks in Ti and V and phase transformation in Ti[J]. Physics of Plasmas, 2004,11(5):2688-2695.

[84] Yaakobi B, Meyerhofer D D, Boehly T R, et al. Dynamic EXAFS probing of laser-driven shock waves and crystal-phase transformations[J]. Physical Review Letters, 2004,92(9):095504.

[85] Yaakobi B, Boehly T R, Meyerhofer D D, et al. EXAFS measurement of iron bcc-to-hcp phase transformation in nanosecond-laser shocks[J]. Physical Review Letters, 2005,95(7):075501.

[86] Smith R F, Eggert J H, Swift D C, et al. Time-dependence of the alpha to epsilon phase transformation in iron[J]. Journal of Applied Physics, 2013,114(22):223507.

[87] Smith R F, Minich R W, Rudd R E, et al. Orientation and rate dependence in high strain-rate compression of single-crystal silicon[J]. Physical Review B, 2012,86(24):245204.

[88] Smith R F, Eggert J H, Rudd R E, et al. High strain-rate plastic flow in Al and Fe[J]. Journal of Applied Physics, 2011,110(12):123515.

[89] Coppari F, Smith R F, Eggert J H, et al. Experimental evidence for a phase transition in magnesium oxide at exoplanet pressures[J]. Nature Geoscience, 2013,6(11):926-929.

[90] Pang Wei-wei, Zhang Ping, Zhang Guang-cai, et al. Morphology and growth speed of hcp domains during shock-induced phase transition in iron[J]. Nature Scientific Reports, 2014,4:03628.

[91] Yu Ji-dong, Wang Wen-jiang, Wu Qiang. Nucleation and growth in shock-induced phase transitions and how they determine wave profile features[J]. Physical Review Letters, 2012,109(11):115701.

[92] Smith R F, Minich R W, Rudd R E, et al. Orientation and rate dependence in high strain-rate compression of single-crystal silicon[J]. Physical Review B, 2012,86(24):245204.

[93] Jensen B J, Rigg P A, Knudson M D, et al. Dynamic compression of iron single crystals[C]∥Furnish M D, Elert M, Russell T P, et al. Shock Compression of Condensed Matter-2005: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter. Baltimore, Maryland (USA): American Institute of Physics, 2006,845(1):232-235.

(责任编辑 张凌云)

Progress in high-power laser ramp compression of solids

Li Mu, Sun Cheng-wei, Zhao Jian-heng

(InstituteofFluidPhysics,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China)

Laser-induced stress waves can deliver ramp compression on solid materials with very high strain rates, and it is one of the newly-developed dynamic high-pressure methods in decades. Distinct from the conventional methods, laser ramp compression can reach terapascal pressures smoothly from ambient pressure with a high strain rate 106-109s-1, but the sample is still in solid state. During the rapid loading process, the thermodynamic state, dynamic characteristics, and in situ microstructure can all be probed by the advanced diagnostic technology. This method is becoming an important and new approach to further investigation on high-pressure physics, equation of state, and rate-dependent material dynamics. In this paper, the history, principle, diagnostics and main breakthroughs of laser ramp compression are reviewed and expected.

mechanics of explosion; ramp compression; high-power laser; solids; equation of state; rate dependent

10.11883/1001-1455(2015)02-0145-12

2014-12-26；

2015-02-20

国家自然科学基金项目(11172280,11472255)

李 牧(1979— )，男，博士，副研究员; 通讯作者： 赵剑衡,jianh_zhao@sina.com。

O381 国标学科代码： 13035

A