客车侧翻一步碰撞算法中初始解预测方法的研究*

王 童，那景新，张苹苹

(吉林大学，汽车仿真与控制国家重点实验室，长春 130022)



2015154

客车侧翻一步碰撞算法中初始解预测方法的研究*

王 童，那景新，张苹苹

(吉林大学，汽车仿真与控制国家重点实验室，长春 130022)

在作者先前开发的客车侧翻一步碰撞算法的基础上，提出一种基于结构变形标准模板和节点坐标插值的初始解预测方法，以提高其计算效率。通过对12m公路客车典型车身段模型进行模拟，并与原始侧翻一步碰撞算法和侧翻试验结果对比，验证了该方法的有效性。

客车侧翻一步碰撞算法；结构变形标准模板；节点坐标插值；初始解预测

前言

侧翻是客车最严重的事故类型之一，往往造成群死群伤的恶劣后果[1]。客车侧翻一步碰撞算法，是作者参考板料冲压一步成形算法的核心思想[2-4]，提出的一种用于客车侧翻碰撞的新算法[5]。该算法同样基于非线性全量理论，并利用了侧翻碰撞过程中的能量转换关系。与现有的Ls-dyna等增量法软件相比，在略微牺牲一点计算精度的情况下，大幅提升了计算效率。目前算法程序已调试成功，可在客车车身设计初期，对结构侧翻安全性进行快速初步评价，从而缩短产品的开发周期。

算法须在最大变形状态下获得满足能量转换和变形条件的初始解，以进行Newton-Raphson迭代。采用作者首次提出的“基于最大惯性力加载的初始解预测算法”，通过求解弹性有限元结构近似平衡方程，并结合侧翻碰撞过程中的能量转换关系，获得满足变形条件的迭代初始解。理论上该初始解的精度对算法模拟结果没有影响，但它越接近真实最终变形，算法的计算效率越高。

为此，本文中提出一种基于结构变形标准模板节点坐标插值原理的初始解预测方法。既提高了初始解预测的精度，同时算法计算的工作量大大减少，计算效率得到显著提高。

1 侧翻一步碰撞算法基本理论

侧翻一步碰撞算法基于非线性全量理论和比例加载假定，依据ECE R66法规[6]，忽略了中间状态和构形的变化[7]，只考虑结构碰撞开始和最大变形两个状态。在结构的最大变形状态得到满足变形条件的初始解，并采用Newton-Raphson法迭代求解[8]，快速获得结构的最终变形。

将碰撞开始状态的结构作为原始构形{X}，此时车体未发生变形。由于侧翻一步碰撞算法中，结构的最大变形是不确定的，故须假定一个最大变形构形{x}。在结构最大变形状态下，各节点的位移{U}为

{U}={x}-{X}

(1)

将满足变形条件的节点位移{U}作为Newton-Raphson迭代初始解。由于车体结构在空间内变形过程无外力作用[9]，此时节点失衡力{R(U)}已处于不平衡状态：

{R(Ui)}={Fext(Ui)}-{Fint(Ui)}=

{0}-{Fint(Ui)}≠{0}

(2)

应用Newton-Raphson法，解决节点失衡力的不平衡问题，得到结构的最终变形。对初始解{U}按照式(3)迭代求解，使式(2)达到平衡：

(3)

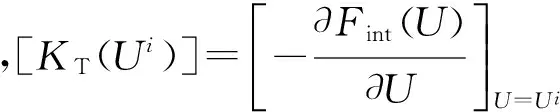
2 初始解预测的标准模板法

为提高客车侧翻一步碰撞算法的初始解预测精度，本文中提出标准模板法。对于标准模板的构造，主要以12m公路客车为例说明，该方法同样适用于其他长度公路客车的标准模板构造。公路客车车身的封闭环结构，对提高整车的侧翻安全性起到决定性作用[10]。故根据12m公路客车车身的封闭环结构构造初始解预测的标准模板，以进行车身段和整车的最大变形构形预测。

客车侧翻碰撞过程中，结构各节点的X方向坐标近似认为始终保持不变。初始解预测标准模板法的基本思想是：利用12m公路客车若干典型封闭环的原始构形和最大变形构形侧翻CAE数据，参考结构变形规律，在YZ平面内，构造一组(原始构形和最大变形构形两个标准模板)几乎可适用于所有12m公路客车侧翻碰撞最大变形构形预测的标准模板；对任一款结构最终变形未知的12m公路客车车身结构，根据原始结构各节点在原始构形标准模板中的位置，应用节点坐标插值法，确定各节点在最大变形构形标准模板中的新坐标，得到结构最大变形构形；再结合原始构形节点坐标，获得满足变形条件的侧翻一步碰撞算法的初始解，进行Newton-Raphson迭代。

2.1 原始构形标准模板建立

为获得结构变形前后的一般运动变形规律和构造最大变形构形标准模板，首先建立结构变形前的原始构形标准模板。为使所建立的标准模板具有一定的通用性，选取3款12m公路客车车身骨架的3个典型封闭环，作为构造原始构形标准模板的参考结构，其有限元模型如图1所示。3个封闭环断面结构的外廓尺寸有微小差别，杆件的截面尺寸和底架的结构形式也有所差异。

图2为3个封闭环原始构形标准模板。根据3个封闭环结构的有限元模型，在3个断面的高宽尺寸中分别选取最大值，并对其进行适当加大处理。最终确定的模板高宽尺寸为3 325mm×2 520mm，将其作为3个标准模板的边界条件。在YZ平面内，将3个封闭环断面均置于上述边界尺寸的模板中，并采用高宽尺寸为175mm×180mm的矩形网格，将模板划分为19行14列的格栅。由于均为12m公路客车结构的封闭环，3个封闭环结构均可很好地适应所构造的标准模板，这些模板基本可以反映所有12m公路客车侧翻前原始结构各节点与模板的相对位置关系。

参考图2构造的3个封闭环原始构形标准模板，对各模板的网格数量、排列形式和网格位置进行对比和整合，获得一个几乎可适用于全部12m公路客车的原始构形标准模板，如图3所示。标准模板的边界尺寸和网格大小，后续可参考更多车型作进一步优化改进，以增强其对12m公路客车的适用范围、求解精度和计算效率。

2.2 最大变形构形标准模板的建立

为对客车侧翻后结构的最大变形构形进行预测，须在图3原始构形标准模板基础上，构造对12m公路客车具有普遍参考意义的最大变形构形标准模板。应用Ls-dyna软件对3个封闭环进行侧翻仿真，从结构的最终变形着手，寻找客车侧翻碰撞后结构变形的一般规律。3个封闭环侧翻仿真的最终变形如图4所示。

将3个封闭环的最终变形分别放入图3构造的原始构形标准模板中，参考结构变形趋势，对模板网格的位置和形状作适当调整，确保模板网格的移动变形趋势与结构变形协调，并保持各网格内的结构节点与在原始构形标准模板中相同，构造出3个封闭环的最大变形构形标准模板，如图5所示。这些模板基本可以反映12m公路客车侧翻后结构的变形形态。

根据图5构造的3个封闭环最大变形构形标准模板，对各模板的网格数量、排列形式和网格位置与形状进行对比和整合，得到一个几乎可反映全部12m公路客车侧翻后结构变形形态的最大变形构形标准模板，如图6所示。应用该模板可进行封闭环、车身段和整车的最大变形构形预测。

这样利用图3和图6所示的一组标准模板，根据原始结构各节点在原始构形标准模板中的位置，应用节点坐标插值法，在最大变形构形标准模板中即可确定结构各节点的新坐标，得到结构的最大变形构形。通过考虑侧翻碰撞过程中的能量转换关系，计算出满足结构变形条件的侧翻一步碰撞算法的初始解。其他长度公路客车的侧翻碰撞最大变形构形预测的标准模板组，构造过程同上所述。

2.3 初始解预测的节点坐标插值法

在用上述标准模板对算法进行初始解预测时，需应用节点坐标插值法求解，具体计算过程如下。

在所构造的图3和图6一组标准模板中，原始构形与最大变形构形同一节点A(a)的对应关系如图7所示。在YZ平面内，假定原始构形中某一节点A的节点坐标为(YA,ZA)，该节点所在图3标准模板中对应网格M的4个节点坐标为I(YIA,ZIA),J(YJA,ZJA),K(YKA,ZKA)和L(YLA,ZLA)。

图7中，结构变形前节点A的坐标可由网格M的4个节点坐标插值得到。由于节点A的坐标已知，图3标准模板的网格M4个节点坐标也已知，插值系数rA和sA可由下式计算：

(4)

整理式(4)得

(5)

由式(5)计算的插值系数，可唯一确定结构各节点在图3标准模板中的位置和坐标。

经过侧翻碰撞后，结构产生变形，但最大变形构形各节点坐标未知，此时引入图6所示的最大变形构形标准模板。图7中，变形前的节点A随网格M移动到变形后的节点a位置，坐标变为(ya,za)，坐标值未知；网格M因形状及位置发生变化，4个节点坐标变为i(yia,zia),j(yja,zja),k(yka,zka)和l(yla,zla)，坐标值已知。结构变形前后，由于节点A(a)与网格M间的相对位置保持不变，故插值系数rA和sA保持不变。

将式(4)中网格M的4节点坐标替换为i(yia,zia),j(yja,zja),k(yka,zka)和l(yla,zla)，结合式(5)，即可确定结构变形后，在图6准模板中的新节点坐标a(ya,za)，得到结构的最大变形构形。再结合结构的原始构形，考虑侧翻碰撞过程中的能量转换关系，计算满足结构变形条件的Newton-Raphson迭代初始解。通过迭代使结构节点失衡力达到平衡，获得结构的最终变形。

3 实例分析

为检验该标准模板法的有效性和模拟效率，选择另一款12m公路客车的典型车身段结构作为研究对象，如图8所示。

用CATIA建立车身段几何模型。为满足仿真模拟精度要求，并节省计算时间，选取10mm大小的shell单元划分网格。模型共离散四边形单元259 976个，节点258 368个，如图9所示。应用所提标准模板法进行初始解预测，代入侧翻一步碰撞算法求解，结构的最终变形云图如图10所示。

应用原始侧翻一步碰撞算法[5]模拟的结构最终变形云图如图11所示，车身段侧翻试验的结构最终变形如图12所示。将图10与图11和图12对比，结构的变形趋势很好地吻合，表明该方法具有较好的实际应用效果，具有一定的参考价值。

为进一步对结构最终变形进行定量对比，选取该车身段的封闭环①和②两侧立柱内侧的若干测点进行数据采集(图8)，3种结果获得的各立柱变形量如表1所示。

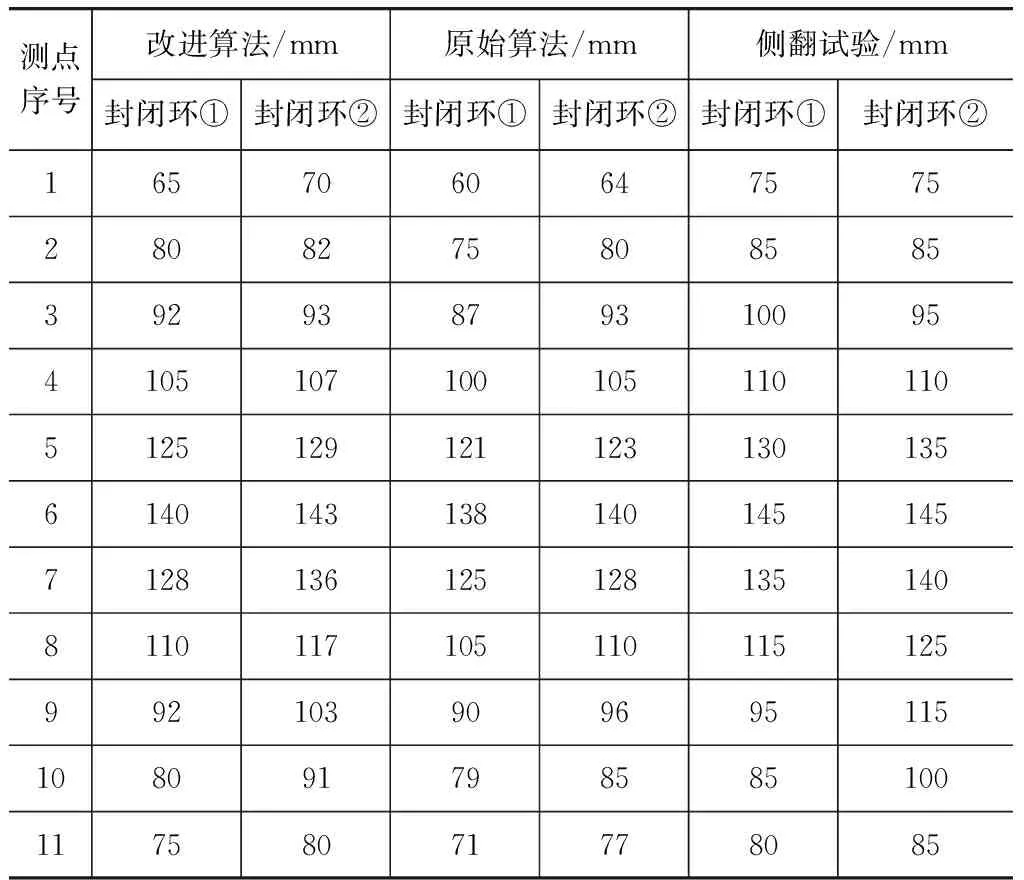
表1 各封闭环两侧立柱变形量统计

图13和图14所示为车身段封闭环①和②两侧立柱的变形量柱状图对比。

对比改进算法与原始算法的模拟时间。改进算法的模拟时间为10min，原始算法为120min，改进算法的模拟时间仅约为原始算法的1/10。

通过上述分析对比发现，3种结果各测点的数据走势基本一致。采用标准模板法改进后的侧翻一步碰撞算法模拟结果，与原始算法及侧翻试验结果的误差小于15%，精度在可接受范围内，且改进后算法的计算时间约为原始算法的10%。在略微牺牲一点计算精度的情况下，大幅提升了计算效率，降低了试验成本，检验了该方法在实际应用中的有效性。

4 结论

提出了一种基于结构变形标准模板节点坐标插值原理的初始解预测方法，将其应用于客车侧翻一步碰撞算法，计算效率得到了显著提高。通过对12m公路客车典型车身段进行研究，检验了该方法的实际应用效果。

但是，标准模板仅适用于12m公路客车的侧翻碰撞的初始解预测，对于其他长度的公路客车车型却不适用。可参考所提方法的思想，对其他车型的标准模板进行设计，从而扩展了标准模板法初始解预测的适用范围。

[1] 周宇,雷正保.客车动态翻滚试验仿真研究[J].汽车科技,2005(5):37-39.

[2] Guo Y Q, Batoz J L, El M M, et al. On the Estimation of Thickness Strains in Thin Car Panels by the Inverse Approach[C]. NUMIFORM’92,1992:1403-1408.

[3] Naceur H, Guo Y Q, Batoz J L, et al. Design of Process Parameters in Deep Drawing of Thin Sheets Using the Simplified Inverse Approach[C]. NUMISHEET’99, France,1999,1:517-522.

[4] Guo Y Q, Naceur H, Debray K, et al. Initial Solution Estimation to Speed up Inverse Approach in Stamping Modeling[J]. Engineering Computations,2003,20(7):810-834.

[5] Na J X, Wang T, Xu Z W. Research on a One-step Fast Simulation Algorithm for Bus Rollover Collision Based on Total Strain Theory[J]. International Journal of Crashworthiness,2014,19(3):275-287.

[6] ECE R66关于核准大型客运车辆上部结构强度的统一技术规范[S].2005.

[7] Guo Y Q, Batoz J L, Naceur H, et al. Recent Developments on the Analysis and Optimum Design of Sheet Metal Forming Parts Using the Simplified Inverse Approach[J]. Computers and Structures,2000,78:133-148.

[8] Huang Y, Chen Y P, Du R X. A New Approach to Solve Key Issues in Multi-step Inverse Finite Element Method in Sheet Metal Stamping[J]. International Journal of Mechanical Sciences,2006,48:591-600.

[9] Tang B T, Zhao Z, Hagenah H, et al. Energy Based Algorithms to Solve Initial Solution in One-step Finite Element Method of Sheet Metal Stamping[J]. Computer Methods in Applied Mechanics and Engineering,2007,196:2187-2196.

[10] 那景新,王秋林,屈丹,等.客车封闭环腰梁接头形式对侧翻安全性的影响[J].吉林大学学报(工学版),2011,41(4):921-926.

A Research on the Initial Solution Prediction Methodfor One-step Bus Rollover Algorithm

Wang Tong, Na Jingxin & Zhang Pingping

JilinUniversity,StateKeyLaboratoryofAutomotiveSimulationandControl,Changchun130022

Based on the one-step bus rollover algorithm previously developed by authors, an initial solution prediction method based on the standard template for structure deformation and the interpolation of nodal coordinates is proposed with an aim to enhance its calculation efficiency. By a simulation on the typical body section model of a 12-m highway coach and comparing its result with that of original one-step rollover algorithm and test data, the effectiveness of proposed method is verified.

one-step bus rollover algorithm; standard template for structure deformation; nodal coordinates interpolation; initial solution prediction

*国家自然科学基金(51075187)资助。

原稿收到日期为2013年12月31日。