线控转向汽车转向盘转角传感器的容错控制策略*

何 磊，马伯祥，宗长富

(1.吉林大学，汽车仿真与控制国家重点实验室,长春 130022； 2.中国第一汽车股份有限公司技术中心,长春 130011)



2015057

线控转向汽车转向盘转角传感器的容错控制策略*

何 磊1，马伯祥2，宗长富1

(1.吉林大学，汽车仿真与控制国家重点实验室,长春 130022； 2.中国第一汽车股份有限公司技术中心,长春 130011)

以多维高斯隐式马尔可夫模型为基础，采用软硬件冗余技术，提出了线控转向汽车转向盘转角传感器的容错控制策略，并通过硬件在环试验进行了验证。结果表明，该策略可应用于线控转向汽车转向盘转角传感器的容错控制，有效提高其安全性和可靠性。

汽车；线控转向；转角传感器；容错控制；隐式马尔可夫模型

前言

为了保证汽车线控转向系统安全可靠地工作，各相关研究机构对线控转向系统的故障诊断和容错控制进行了广泛的研究[1]。汽车线控转向系统容错控制的研究对象主要包括传感器、电机和电控单元3部分。其中，传感器的种类多、故障率高，对它的故障诊断和容错控制研究显得十分重要。

文献[2]中利用传统的卡尔曼滤波器，提出了汽车线控转向系统的传感器容错控制方法；文献[3]中利用滑模观测器，建立了线控转向执行机构传感器的容错控制方法；文献[4]中利用自适应渐消卡尔曼滤波技术，构建了线控转向执行机构传感器的容错控制方法。目前，国内外的研究成果大多是针对线控转向系统中转向执行机构部分的传感器进行的，而针对转向盘转角传感器的容错控制研究还比较少。

本文中将转向盘模块的转角传感器进行了硬件上的冗余设计，以防止单转角传感器故障引起的永久性错误。同时，根据车辆自身状态和转向盘转角信号，使用隐式马尔可夫模型(hidden Markov model, HMM)进行车辆行驶状态的辨识，预测下一时间步的车辆转向盘转角，以软件冗余方式来实现转角传感器的故障定位，将没有故障的转角传感器的测量值作为转向盘转角值，实现转向盘转角传感器的容错控制。

1 线控转向系统的结构

线控转向系统按功能划分，可分为转向盘模块、控制器模块和转向执行模块3部分。具体的线控转向系统结构示意图如图1所示。

转向盘模块将驾驶员的转向意图转换成数字信号，传递给控制器模块，同时接收控制器模块传来的力矩信号，产生转向盘的回正力矩，以提供给驾驶员相应的路感信息。

转向执行模块接收控制器模块的命令，控制转向车轮转动，实现驾驶员的转向意图。

控制器模块对采集的信号进行分析处理，判别汽车的运动状态，向路感模拟电机和转向执行电机发送指令，控制两个电机的工作，保证各种工况下都具有理想的车辆响应，以减少驾驶员对汽车转向特性随车速变化的补偿任务，减轻驾驶员负担。

由于线控转向系统在机械结构上的革新，从动力学角度很难建立转向盘模块与整车之间的关系方程。而转向盘模块又通过转角传感器将驾驶员的转向意图转换成电信号，发送给控制器模块。为避免单个转角传感器故障带来的永久性错误，对转向盘转角传感器进行二倍硬件冗余设计，再利用软件算法预测转角传感器的值，完成对转角传感器的故障定位，从而实现转角传感器的容错控制。

2 多维高斯HMM建模

2.1 隐式马尔可夫模型

隐式马尔可夫模型是在马尔可夫链的基础上发展起来的。它包含双重的随机过程：马尔可夫链和一般的随机过程。在HMM里，状态是不能直接看到的，观察者只能看到基于状态产生的模型的输出(观察序列)。每一个状态与其可能的观察值之间的关系通过一般的随机过程描述；状态间的转移通过马尔可夫链描述[5]。因此，借助这两个随机过程，能透过HMM产生的观察序列，得到状态时间序列和模型的相关信息。

用HMM来处理实际的研究课题时，需要解决以下3个基本问题。

问题1：给定观察序列O=(O1,O2,…,OT)和模型λ，计算P(O|λ)，即计算模型产生观察序列的概率。这可以用来解决评价问题，或检验一个模型与观察序列的匹配程度。问题1通常采用Forward-Backward算法来解决[6]。

问题2：给定观察序列O=(O1,O2,…,OT)和模型λ，确定一个最佳的状态序列Q=(S1,S2,…,ST)，来最好地解释给定的观察序列。问题2可以用来挖掘模型的隐含成分，即找出最优的状态序列(一个辨识问题)。与问题1不同，问题2的解会有很多形式。问题2主要在于最优状态序列的定义，即最优标准的选择。有的优化准则是从单个状态上考虑，有的是从两三个状态上来确定最佳的状态序列，这些优化准则对某些应用是可行的，但最广泛使用的优化准则是从整个状态序列上考虑，即找到最优的状态序列，使得P(Q|O,λ)最大。在实际中并没有一个“最佳”的定义，基于动态编程的Viterbi算法[7]得到的结果通常是满意的，但并不能保证它是绝对意义的“最优”。

问题3：调节模型参数使P(Q|O,λ)最大。

问题1和问题2求解的前提都是已知模型参数λ，可见，确定模型参数对于一个以HMM理论为基础的问题来说，是首要解决的任务。这也就是一个模型的训练过程。即在给定模型初始参数后，利用某种算法对模型参数进行迭代，使观察序列(训练数据)在最终的模型参数下产生的概率最大。HMM模型参数训练应用的算法为Baum-Welch算法[8]。

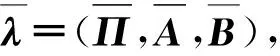
2.2 多维高斯HMM建模和参数确定

鉴于HMM处理时间序列的能力和强的统计学基础，本文中借助驾驶模拟器采集车速、转向盘转角和转向盘角速度的数据，对数据预处理后，用Baum-Welch算法对不同车速下的紧急转向、正常转向和直线行驶工况对应的HMM模型的参数进行优化。然后借助美国国家仪器公司的PXI 1042实时控制器和线控转向试验台，结合HMM用于评估的Forward-Backward算法和优化后的各多维高斯HMM模型，对当前行驶工况进行实时辨识，并预测下一时间步的转角传感器的数据值。通过预测值和传感器采集到的数据比较，验证采集到的传感器数据的正确性。整个模型构建和预测传感器数据的过程如图2所示。

构建多维高斯HMM模型的过程，就是确定模型参数的过程。HMM模型可由向量λ描述：

λ=[Q,N,Π,aij,bj(k)]

(1)

式中：Q={Q1,Q2,…,QT}为模型中马尔可夫链的状态，代表特定速度下的某转向操作的不同等级的小操作；N为每个状态下对应可能的观察值数目；П为初始概率矩阵，即t=1时，各个状态出现的概率；aij=P(st+1=qj/st=qi)，i,j=1,2,…,N，为从状态i到状态j的状态转移概率；bj(k)为观察值概率矩阵，即在状态i下，产生观察值k的概率。

观察值概率矩阵决定模型是离散HMM或是连续HMM。对于离散HMM，bj(k)为对应矢量量化码的概率矩阵；对于连续HMM，bj(k)为描述状态i特征矢量分布的概率密度函数。考虑到采集的转向盘转角、转向盘角速度和车速传感器信号都是连续信号，为防止信号量化时造成的信号失真，本文中应用多维高斯HMM理论训练各个驾驶工况对应的HMM模型，于是有

(2)

式中：M为观察序列中的混合分量的个数，本文中共有转向盘转角、转向盘角速度和车速3个混合分量；cim为对应状态i的第m个混合分量的混合系数；N[O，μim，Uim]为高斯函数，μim，Uim分别为高斯函数的平均值和协方差。O为观察值，可表达为

O(t)={a(t),b(t),c(t)}

(3)

式中a(t)、b(t)和c(t)分别为转向盘转角、转向盘角速度和车速。

根据一定车速范围内的转向盘传感器信号O和采用K-means算法[9]获得的模型初始参数，运用Baum-Welch重估算法的递归思想，采用一种最大似然估计的方法，逐步迭代，使观察值O相对于模型λ发生的概率P(O|λ)逐渐增大，直到P(O|λ)收敛到一个定值，此时的λ即为所求的模型参数向量。

不同速度段的各个驾驶工况对应的多维高斯HMM模型的参数全部优化完成后，应用Forward-Backward算法，实时采集的转向盘传感器数据和车速对所有的多维高斯HMM模型进行评估，选择发生概率最大的多维高斯HMM作为当前驾驶工况。

选取对应当前驾驶工况的多维高斯HMM模型的参数，并在实时采集来的传感器数据后面添加各种可能发生的数据，构成预测观察序列集。应用Forward-Backward算法，选取最可能发生的观察序列，从而预测出下一时间步的转向盘转角传感器的数据值。

3 转角传感器的容错控制方法

根据预测出的下一时间步转角传感器的数值，结合两个转角传感器的数值，可确定故障传感器的位置。具体过程如图3所示。

转角传感器A与B的数值相同时，故障决策判定转角传感器无故障；当转角传感器A与B的数值不同时，判定为有故障。此时，采集车辆状态信息，综合计算多维高斯HMM模型辨识出的转角传感器的数值，判定双转角传感器故障情况。确定故障转角传感器位置的同时，将未发生故障的转角传感器的数值作为转向盘转角值，从而实现转向盘转角传感器的容错控制。

利用多维高斯HMM模型的软件冗余和转角传感器的硬件冗余，进行转向盘转角传感器的容错控制，方法可靠简单且方便易行。

4 试验验证与结果分析

对多维高斯HMM模型分车速段进行参数标定，每10km/h为一段，100km/h以上的高车速段模型参数设置为相同值。为保证试验安全性，在搭建的硬件在环试验台上进行参数标定。线控转向硬件在环试验台主要包括转向盘模块、控制器模块、转向执行模块、驾驶模拟器、阻力模拟模块和阻力模拟控制器。具体的硬件在环试验台的结构图见图4。

其中，驾驶模拟器提供29自由度的车辆模型，能够较为准确地提供车辆运动状态信号。阻力模拟模块根据驾驶模拟器的转向状态，折算出前轮转向阻力矩，通过阻力模拟控制器加载到前轮转向执行机构上。

因篇幅的限制，未列出所有车速段的参数。以70～80km/h速度段的正常转向为例，给出离线训练得到的模型参数如下，并在此车速段下进行故障模拟和容错控制试验。

Π=[0.5706,0.2857,0.1437]

无论何种突发故障，转角传感器故障的表现形式都是实际值与测量值之间的差异。为了更加直观地显示容错控制结果，这里以传感器信号线断路为例，模拟传感器的故障，并在已有的线控转向硬件在环试验台上进行了试验。

故障模拟是在驾驶员的连续驾驶操作过程中加入的。在未加入故障前，线控转向系统正常工作，两个转向盘转角传感器的测量值与基于多维高斯HMM算法计算出的预测值相同，验证了算法的准确性，如图5所示。对标准转向盘转角传感器加入故障后，可以观察到它的测量值与冗余传感器的测量值产生明显的差异，而算法计算出的预测值与冗余传感器的测量值基本相同，如图6所示。

5 结论

采用转向盘转角传感器二倍冗余结构，避免单传感器故障带来的永久性控制错误。以多维高斯隐式马尔可夫算法为基础，构建了线控转向汽车转向盘转角传感器的容错控制方法。根据车辆状态信息和转向盘传感器信号，使用隐式马尔可夫模型来进行车辆行驶状态的辨识，预测下一时间步的车辆转向盘的转角和角速度，从而判断新采集到的转向盘转角传感器信号是否出现异常。当出现异常时，综合比较两个转向盘传感器的测量值与预测值，对转向盘转角传感器故障情况予以确认，并进行容错控制。硬件在环试验结果表明：基于多维高斯HMM算法的转向盘转角传感器容错控制方法应用于线控转向汽车，能够有效提高线控转向汽车转向盘转角传感器的安全性与可靠性。

[1] Gadda C D, Laws S M, Gerdes J C. Generating Diagnostic Residuals for Steer-by-wire Vehicles[J]. IEEE Transactions on Control Systems Technology,2007,15(3):529-540.

[2] Gadda C D, Yih P, Gerdes J C. Incorporating a Model of Vehicle Dynamic in a Diagnostic System for Steer-by-wire Vehicles[C]. Arnhem, the Netherlands,2004:779-784.

[3] Hasan M S, Anwar S. Sliding Mode Observer and Long Range Prediction Based Fault Tolerant Control of a Steer-by-wire Equipped Vehicle[C]. SAE Paper 2008-01-0903.

[4] 田承伟,宗长富,王祥,等.线控转向汽车传感器的容错控制[J].吉林大学学报(工学版),2010,40(1):6-12.

[5] Zong Changfu, Wang Chang, Yang Hsiao. Driving Intention Identification and Maneuvering Behavior Prediction of Drivers on Cornering[C]. IEEE ICMA, Aug,2009:4055-4060.

[6] Rabiner L. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition[C]. IEEE,1989,77(2):257-286.

[7] Vaseghi S V. State Duration Modeling in Hidden Markov Models[J]. Signal Processing,1995,41(1):31-41.

[8] Huang X D, Jack M A. Semi-Continuous Hidden Markov Models for Speech Signals[J]. Computer Speech and Language,1989,3(3):239-251.

[9] Stuart Russell, Peter Norvig. Artificial Intelligence: A Modern Approach (3rd Edition) [M]. London: Prentice Hall,2009.

Fault-tolerance Control Strategy for the Steering WheelAngle Sensor of a Steer-by-wire Vehicle

He Lei1, Ma Boxiang2& Zong Changfu1

1.JilinUniversity,StateKeyLaboratoryofAutomobileSimulationandControl,Changchun130022;2.R&DCenter,ChinaFAWCo.,Ltd.,Changchun130011

Based on multi-dimension Gaussian hidden Markov model and by adopting hardware and software redundancy techniques, a fault-tolerance control strategy for the steering wheel angle sensor of a steer-by-wire vehicle is proposed and verified by a hardware-in-the-loop experiment. The results demonstrate that the strategy proposed can be applied to the fault-tolerance control of steering wheel angle sensor in a steer-by-wire vehicle, effectively improve the safety and reliability of the angle sensor.

vehicle; steer-by-wire; rotation angle sensor; fault-tolerant control; hidden Markov model

*国家自然科学基金(50775096)资助。

原稿收到日期为2013年4月6日，修改稿收到日期为2013年11月4日。