基于NSGA-II算法的磁流变悬置磁路多目标优化*

邓召学，郑 玲，李以农，张东东，付江华，陈代军

(1.重庆大学，机械传动国家重点实验室，重庆 400030; 2.长安汽车工程研究院，重庆 401120)



2015099

基于NSGA-II算法的磁流变悬置磁路多目标优化*

邓召学1，郑 玲1，李以农1，张东东1，付江华2，陈代军2

(1.重庆大学，机械传动国家重点实验室，重庆 400030; 2.长安汽车工程研究院，重庆 401120)

以磁流变悬置的磁路体积最小、输出阻尼力最大为优化目标，基于ANSYS参数化设计语言(APDL)建立了磁流变悬置磁路结构的多目标优化模型，采用带精英策略的快速非支配排序遗传算法(NSGA-II)进行优化，获得了磁路结构的Pareto最优解，并采用模糊集合理论对Pareto最优解进行选优。根据优化前后的磁路结构尺寸加工了两个磁流变悬置，并对悬置动态性能进行试验。结果表明：所提出的磁流变悬置磁路多目标优化方法是正确有效的，能够获得更加紧凑的磁流变悬置磁路结构，并提高悬置的输出阻尼力。

磁流变悬置；磁路；多目标优化；NSGA-II算法

前言

磁流变悬置是以磁流变液为载体构成的汽车动力总成振动半主动控制装置，在磁场作用下，磁流变液体流变特性迅速改变[1]，从而使悬置阻尼力在较宽范围内可控。半主动智能磁流变液悬置由于结构简单、能耗小、成本低等因素，已经成为当前汽车工业研究和应用的热点之一[2-4]。作为汽车动力总成悬置系统的关键器件，磁流变悬置的磁路结构设计直接关系到悬置的输出阻尼力调节范围，从而影响整个悬置系统的隔振性能。因此，对磁流变悬置磁路结构优化，保证磁流变悬置发挥最大工作效能、满足动力总成隔振要求，成为悬置系统设计与开发的重要环节。

目前，包括磁流变悬置在内的磁流变阻尼器磁路结构设计主要依据Bingham模型，以满足阻尼力调节范围、调节系数或磁路体积等为目标，确定磁流变阻尼器的主要结构参数。文献[5]～文献[7]中采用有限元方法对磁流变阻尼器磁路结构进行了单目标优化，但单目标优化很难满足磁流变悬置的总体要求；文献[8]中将输出阻尼力、阻尼力调节系数等多目标简化成一个带正权重系数的单目标函数，而权重系数由决策者决定，权重的选取缺少理论依据并且很难在解空间内搜索到最优解，而阻尼力是在阻尼通道磁感应强度最大的理想条件下得到的，计算准确度较低。

针对上述问题，本文中提出将ANSYS参数化设计语言(APDL)和带精英策略的快速非支配排序遗传算法(NSGA-II)相结合，以磁流变液悬置输出阻尼力和磁路体积为优化目标，阻尼力可调系数、阻尼通道内磁流变液和磁芯的磁感应强度为约束条件，进行了多目标优化，以进一步改善磁流变悬置的性能。

1 基于APDL的NSGA-II算法

对于多目标优化问题，各优化目标之间往往相互矛盾，很难得到使所有目标都达到最优的解，不存在唯一的全局最优解，而是存在多个最优解的集合，因此引入Pareto非劣解的概念。NSGA-II是Deb等人在NSGA的基础上提出的带精英策略的非支配排序遗传算法，该方法基于分级的快速非支配法来降低算法的复杂程度，并利用拥挤度和拥挤度比较算子作为排序后同级间的胜出标准，同时还引入精英策略来增大采样空间，克服了传统NSGA的计算复杂和共享参数难以确定的缺点，提高了算法的收敛性、鲁棒性和计算效率[8-9]。

本文中以NSGA-II算法作为优化系统，以APDL作为分析系统，对磁流变悬置磁路结构进行多目标优化。该方法具有以下优点：(1)采用NSGA-II算法作为优化系统的主程序，加快收敛速度，提高求解效率；(2)实现了MATLAB与ANSYS有限元软件的程序接口，使NSGA-II优化程序直接调用APDL命令流进行结构分析，APDL命令流包含了磁路结构的建模、网格划分和后处理；(3)具有较强的通用性，可以对磁流变悬置结构的尺寸、质量、体积和输出阻尼力等目标进行优化设计。

基于APDL和NSGA-II算法的磁流变悬置磁路结构多目标优化原理如图1所示。首先，NSGA-II产生初始设计方案，把方案参数(设计变量值)以.txt文件形式保存在变量文件内；其次，APDL分析程序读取变量文件内容，把计算结果以.txt文件形式保存在目标文件内；最后，NSGA-II读入目标文件内容，确定寻优方向，提出新的设计方案，继续循环迭代计算，程序终止条件设定为达到预定的迭代次数，并最终得到优化结果。

2 磁流变悬置磁路优化模型

2.1 磁流变悬置结构设计

针对某动力总成悬置系统设计了基于流动模式的磁流变悬置，如图2所示。上外磁芯、下外磁芯和内磁芯材料均为DT4，上外磁芯、下外磁芯和内磁芯之间构成环形阻尼通道，阻尼通道内充满磁流变液体，上外磁芯和下外磁芯中部缠绕200匝励磁线圈，当励磁电流改变时，环形阻尼通道内的磁流变液体流变特性也随之改变，从而达到连续调节悬置输出阻尼力的目的。

2.2 建立悬置磁路优化数学模型

磁路设计的优劣直接影响磁流变液悬置的隔振性能。磁路设计的总体目标为尽可能提高磁流变液工作间隙处的磁感应强度和推迟各材料磁饱和的发生，保证结构紧凑,提高悬置输出阻尼力，充分发挥磁流变液体的可控性能。

(1)目标函数

根据动力总成对磁流变悬置性能的要求，以悬置输出阻尼力Fmr的倒数f1和磁芯的体积f2为目标函数，即

F(X)=(f1,f2)T

(1)

流动模式的磁流变液悬置阻尼力由两部分组成，即黏性阻尼力和可控阻尼力，图3为磁流变悬置磁路结构示意图。磁流变液悬置输出阻尼力计算公式[10]为

(2)

式中：Fμ为黏性阻尼力；Fτ为可控阻尼力；Ap为等效泵液面积；τy为磁流变液剪切屈服强度；L为阻尼通道有效长度，L=2(L1+L3)；c为磁流变效应系数，一般取2～3；μ为零场黏度；b为阻尼通道等效周长，b=2π(r1+r2)；h为阻尼通道宽度，取2mm。

目标函数f1为

f1=1/Fmr

(3)

参照图3，可得磁芯的体积为

f2=π[(r1+r2+h+r3+r4)2-(r1+r2+h+r3)2](L2+2L3)+π[(r1+r2+h+r3)2-r22][2(L1+L3)+L2]

(4)

式中：r1为内磁芯内径；r2为内磁芯厚度；r3为线圈槽深度；r4为外磁芯厚度；L1为上、下外磁芯凸台高度；L2为线圈槽高度；L3为上、下外磁芯肩厚度；h为阻尼通道宽度。

(2)设计变量

设计变量为

X=[r1r2r3r4L1L2L3]

设计变量形式上是连续变量，但取值受到机械加工精度、设计规范的约束，为此对设计变量离散化，只保留染色体译码的小数后一位，即以0.1mm作为工程设计精度。通过拆卸液压悬置，对液压悬置内部结构尺寸进行了测量，初步确定了磁流变悬置阻尼通道及其磁路结构尺寸大小。设计变量取值范围如表1所示。

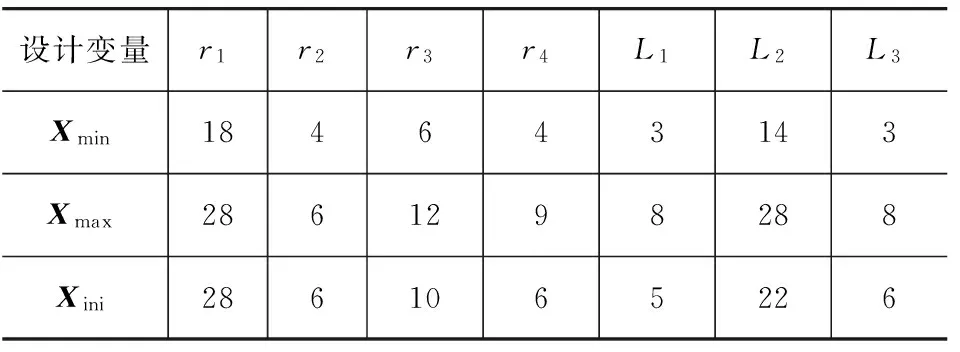
表1 设计变量取值范围及初始设计值 mm

表1中，Xmax、Xmin为设计变量的上、下限值，Xini为其初始设计值。

(3)约束条件

为保证磁流变悬置输出阻尼力具有较宽的可调范围，磁路设计应保证可控阻尼力与黏性阻尼力的比值即可调系数E较大。磁流变液体的磁导率与DT4磁导率相差较大，而且均呈现非线性变化，磁路设计应保证悬置阻尼通道内磁流变液接近饱和而磁路其他部分材料即DT4未达到饱和。磁流变液和DT4的饱和磁感应强度分别为0.65和1.6T。

图4为1/4磁路模型，阻尼通道36个节点平均磁感应强度B1mena为

(5)

式中：B1i为阻尼通道磁流变液各节点磁感应强度。

由式(2)可得阻尼力可调系数为

(6)

最后得到多目标优化问题的约束方程为

(7)

式中：B1max和B2max分别为磁流变液节点和DT4 节点的最大磁感应强度。

3 优化结果

基于APDL和NSGA-II组合优化方法对自行设计的磁流变悬置磁路结构进行优化。NSGA-II优化算法的控制参数：种群规模为100，交叉概率为0.8，变异概率为0.1，最大进化代数为50。经过50代运算，得到了悬置磁路的多目标优化Pareto最优解，如图5所示。

由图5可知，磁芯体积与输出阻尼力倒数这两个目标函数之间的关系是一个目标函数值的降低以另一个目标函数值的增加为代价。因此合理选取Pareto非劣解中的个体作为最优个体显得尤为重要。表2为Pareto最优解集域的部分解。

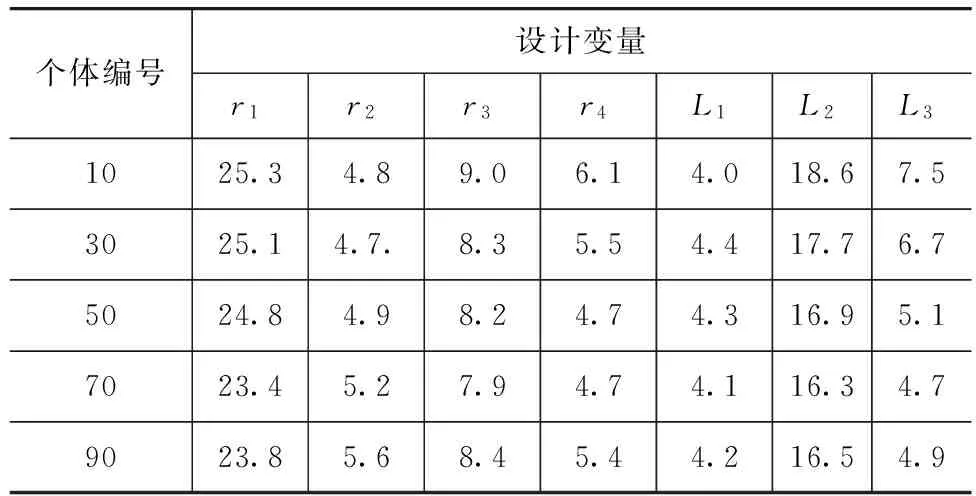
表2 设计变量的部分解集域 mm

3.1 基于模糊集合理论的Pareto解选优

人工Pareto解集选优存在多种不确定的主观因素，因此采用模糊集合理论对多目标优化的Pareto解集进行选优[11]。模糊集合理论基于模糊机制有效地帮助决策者选取Pareto解中的“最优”结果作为折中方案。

定义隶属函数μi为

(8)

式中：fmaxi和fmini分别为第i个优化目标的最大值和最小值；fi为第i个优化目标的取值。对于Pareto集中的每一个非支配解k，定义支配函数Φk为

(9)

式中：Mp为Pareto集所包含解的个数,Mp=100；Mo为优化目标的个数，Mo=2。

根据式(9)，可以计算Pareto最优解集中每个个体的支配值Φk，Φk越大，表示该解的综合性能越好，因此，选择具有最大Φk值的解作为Pareto集的最优解。如图6所示，选取支配函数值最大的71号个体作为最符合要求的最优个体，其对应的最优个体的设计变量结果如表3所示。Xopt为优化后的磁路相关尺寸参数。

表3 设计变量优化值 mm

3.2 优化结果对比

根据表1中的磁路结构的初始设计值和表3中磁路结构优化尺寸，分别建立初始模型、优化模型进行有限元分析，得到优化前后磁路磁感应强度分布，如图7和图8所示；根据图4所示的阻尼通道中节点分布，得到优化前后36个节点磁感应强度曲线，如图9和图10所示；优化前后目标函数悬置输出阻尼力、磁芯体积变化情况如表4所示。

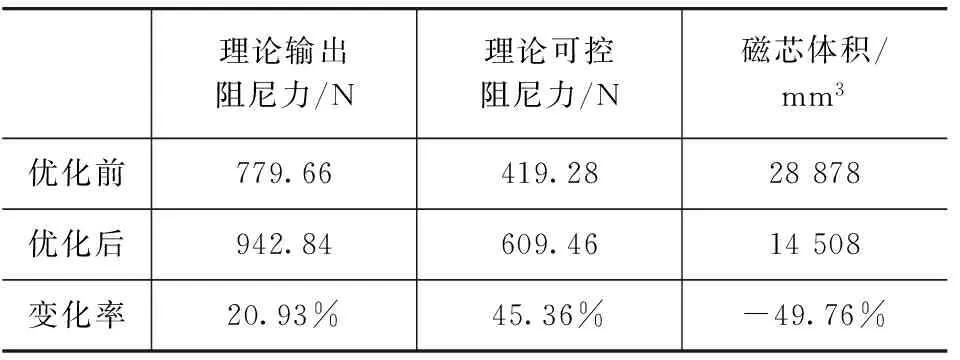
表4 优化前后设计目标结果对比(I=1A)

从图7和图8可以看出，优化后整个磁路的磁感应强度分布更加均匀合理，各部分磁感应强度最高值更接近但未超过磁感应饱和值，说明各部分磁路材料利用率高，使结构更为紧凑。

由图9和图10可知，经过遗传算法进化50代优化后，不同节点处的磁感应强度都得到了较大提高，阻尼通道处的均磁感应强度由0.488 5T提高到0.616 7T，提高了26.2%。

由表4可知，当电流最大为1A时，优化后磁流变悬置理论输出阻尼力为942.84N，相对优化前的779.66N提高了20.93%，理论可控阻尼力也提高了45.36%，说明优化方法对提高阻尼通道内磁流变液磁感应强度效果明显，保证了磁流变悬置具有更宽的可调能力；优化后磁芯体积减小了49.76%，整个磁路结构更加紧凑。

4 试验验证

根据初始磁路尺寸和磁路优化尺寸，加工、装配了两个磁路结构不同的磁流变悬置，采用CRIMS电液伺服试验机对两个磁流变悬置进行动态性能试验，如图11所示。试验共采集了行程为 1mm，频率范围为1～30Hz，间隔为1Hz，电流为 0和1.0A 时的试验数据，如图12所示。

由图12可知，电流不变的情况下，随着激励频率的提高，悬置输出阻尼力幅值逐渐增大，符合一般液压悬置动刚度的变化趋势。频率不变的情况下，随着电流的增大，磁流变悬置输出阻尼力幅值增大，说明磁流变悬置具有较好的可控性。当电流为0时，优化后的悬置零场输出阻尼力幅值略有增大；当电流为1.0A时，优化后的悬置输出阻尼力幅值明显增大，说明磁流变悬置磁路结构的优化具有明显的效果。

图13为不同激振频率下，优化前后悬置可控阻尼力幅值曲线。由图可见，随着频率的提高，磁流变悬置的可控阻尼力先增大后减小，且优化后的可控阻尼力明显增大。通过优化，激振频率为15Hz时的磁流变悬置可控阻尼力幅值从原来的107N增加到167N，增幅为56%，说明了基于APDL和NSGA-II的多目标优化算法是有效的。

与表4对比可见，试验结果的输出阻尼力和可控阻尼力分别远小于计算的输出阻尼力和可控阻尼力，这主要是由于Bingham模型的简化和阻尼通道磁感应强度有限元求解误差造成的。

5 结论

(1)本文中提出采用NSGA-II算法，以悬置输出阻尼力和磁芯体积为目标函数进行多目标优化，避免了以往优化过程中的诸多不足。

(2)考虑经验选择Pareto最优解的不确定性和主观性，提出采用模糊集合理论对Pareto最优解进行选优，以个体支配函数值大小来衡量优化所得的Pareto最优解集个体的优越性，为“最优”个体的选取提供了理论依据。

(3)优化后整个磁路的磁感应强度分布更加均匀合理，磁流变悬置理论输出阻尼力相对优化前有了较大提高，优化后磁芯体积小于优化前磁芯体积，整个磁路结构更加紧凑。

(4)对两种不同尺寸的磁流变悬置进行了加工、装配，并分别进行了动态性能试验验证。试验结果表明，优化后磁流变悬置输出阻尼力和可控阻尼力有较大提高，验证了磁路设计的正确性和优化算法的有效性；但计算的磁流变悬置输出阻尼力和可控阻尼力值相对试验结果有较大的误差，主要是由于Bingham模型所做的简化模型和阻尼通道磁感应强度有限元求解误差造成的，有待今后在进一步研究中修正模型，提高计算精度。

[1] Koo J H, Goncalves F D， Ahmadian M. A Comprehensive Analysis of the Response Time of MR Dampers[J]. Smart Materials and Structures， 2006,15(2):351-358.

[2] Breese D G，Gordaninejad F.Semi-action，Fail-safe Magneto-rheological Fluid Dampers for Mountain Bicycles[J].International Journal of Vehicle Design，2003，33(1/2/3):128-138．

[3] Ericksen E O，Gordaninejad F.A Magneto-rheological Fluid Shock Absorber for an Off-roadmotorcycle[J].International Journal of Vehicle Design，2003,33(1/2/3):139-152．

[4] Gordaninejad,Faramarz,Kelso,et al.Magneto-rheological Fluid Shock Absorbers for HMMWV[C].Proceedings of SPIE-The International Society for Optical Engineering,2000,3989:266-273.

[5] 邓晓毅，石明全.磁流变减振器磁路结构的优化[J].计算机仿真，2010，27(9)：291-293.

[6] 张进秋，彭志召.叶片式磁流变液减振器结构设计与优化[J].振动、测试与诊断，2013，33(1)：132-137.

[7] 郑玲，李以农.磁流变减振器磁路设计与结构优化[J].振动工程学报，2008，21(2):173-178.

[8] Deb K,Agrawal S,Pratab A,et al.A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective: NSGA-II[J].Evolutionary Computation,2002,6(2):182-197.

[9] Gaurav Verma, Arun Kumar, Krishna K Mishra.A Novel Non-dominated Sorting Algorithm[J]. Swarm, Evolutionary, and Memetic Computing Lecture Notes in Computer Science, 2011, 7076:274-281.

[10] 陈杰平，陈无畏.单出杆汽车磁流变减振器设计及试验[J].农业机械学报，2009，40(3):5-10.

[11] Abido Ma．Multiobjective Evolutionary Algorithmsfor Electric Power Dispatch Problem[J].IEEE Transactions on Evolutionary Computation，2006，10(3):315-329.

Multi-objective Optimization for the Magnetic Circuit of Magneto-rheological Mount Based on NSGA-II Algorithm

Deng Zhaoxue1，Zheng Ling1，Li Yinong1，Zhang Dongdong1，Fu Jianghua2& Chen Daijun2

1.ChongqingUniversity,StateKeyLaboratoryofMechanicalTransmission，Chongqing400030;2.ChanganAutoGlobalR&DCenter,Chongqing401120

With minimizing the volume of magnetic circuit structure and maximizing its output damping force as optimization objectives, a multi-objective optimization model for the magnetic circuit structure of magneto-rheological (MR) mount is established with ANSYS parametric design language (APDL). An optimization is conducted with the fast elitist non-dominated sorting genetic algorithm (NSGA-II) and a pareto optimal set is obtained, from which the best compromise solution is extracted based on fuzzy set theory. Two MR mounts with magnetic circuit structures before and after optimization are manufactured respectively and tested on their dynamic performance. The results show that the multi-objective optimization scheme proposed is correct and effective in achieving a more compact magnetic circuit structure with an increased output damping force.

magneto-rheological mount; magnetic circuit; multi-objective optimization;NSGA-II algorithm

*中央高校基本科研项目(CDJZR13280074)、重庆大学机械传动国家重点实验室自主项目(0301002109165)和汽车噪声振动以及安全技术国家重点实验室开放基金资助。

原稿收到日期为2013年7月4日，修改稿收到日期为2013年12月23日。