矿用车车架结构的静动态多目标拓扑优化*

臧晓蕾，谷正气,2，米承继，伍文广，蒋金星，王玉涛

(1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.湖南工业大学，株洲 412007)



2015101

矿用车车架结构的静动态多目标拓扑优化*

臧晓蕾1，谷正气1,2，米承继1，伍文广1，蒋金星1，王玉涛1

(1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.湖南工业大学，株洲 412007)

为了实现行驶工况极为恶劣的矿用车的车架结构的静动态多目标拓扑优化，以静态多工况下刚度和动态多个低阶频率为目标函数，提出了一种车架多目标拓扑优化方法。基于变密度法建立车架结构拓扑优化模型，采用折衷规划法确定多工况刚度拓扑优化目标函数，以平均频率法确定振动频率目标函数，并利用层次分析法选定子目标权重。优化结果显示车架的刚度和固有频率均有提高。对优化后的新车架和原车架进行疲劳寿命的对比分析，结果表明：采用多目标拓扑优化后车架的疲劳寿命明显提高，改善了车架的使用性能。

车架结构；变密度法；层次分析；多目标拓扑优化

前言

矿用车属于非公路运输车辆，其行驶环境恶劣，而车架作为主要承载部件，其结构直接影响整车的性能和使用年限，因此对车架结构的优化就显得尤为重要。车架结构的优化包括拓扑优化、尺寸优化和形状优化，其中，结构的拓扑形状起主导作用，拓扑优化已经成为复杂结构和部件优化的关键技术。

目前连续体的拓扑优化主要以单目标优化问题[1-3]为研究对象，大多以柔度为目标函数，并对新设计的车架进行简单的固有频率分析，或以柔度和1阶特征频率为目标进行优化[4-5]，但忽略了1阶固有频率最高时低阶固有频率交替所产生的振荡问题和权重因子的合理分配问题。

针对车架结构的多目标拓扑优化问题，本文中提出以静态多工况刚度和动态多个低阶频率为优化目标，在验证多体动力学模型合理的基础上通过仿真获得可靠的载荷值，采用层次分析法确定权重因子，基于变密度法实现了车架结构的多目标拓扑优化，改善了车架的强度和动态特性，并将经验设计下的车架与新车架的疲劳寿命进行了对比分析。

1 基于SIMP的拓扑优化模型

1.1 SIMP密度插值法

变密度法[6]的实质是将拓扑设计变量依附于单元材料，有利于基于连续变量的优化算法。人为假定一种实际工程中并不存在的密度可变材料单元，依据离散化的拓扑优化建模思想，这种材料单元的密度设置为[0,1]之间的连续变量，如此将离散变量优化问题转化为更易求解的连续变量优化问题。

为保证优化结果的可制造性和后续优化的进行，SIMP模型中引入了惩罚系数P对中间密度材料进行惩罚。惩罚后的材料单元密度值将更加快速地向“0”或“1”聚集，使SIMP模型能够更好地逼近基于离散变量的拓扑优化模型。

1.2 静态多工况刚度拓扑优化目标函数

在静态拓扑优化问题中，常见的结构响应量为静态刚度，通常把刚度最大问题等效为柔度最小问题，柔度则用应变能来定义。相同的优化参数不同工况下对应的最小应变能拓扑结构差异大，本文中将静态多工况刚度拓扑优化按多目标函数优化问题求解，一般情况下使所有目标函数都能达到最优的“理想解”是不存在的，但可以找到各目标函数综合指标最优的“满意解”，即Pareto最优解。

本文中采用折衷规划将“满意解”和“理想解”之间的距离作为多目标函数的综合评价指标，则静态多工况刚度拓扑优化数学模型[5]为

(1)

式中：ρ为材料密度；n为载荷工况总数；Ωk为第k个工况的权重因子；Ck(ρ)为第k个工况的应变能目标函数；Ckmax和Ckmin分别为第k个工况应变能的最大值和最小值；q为欧式度量，用来度量“满意解”与“理想解”的贴近程度，这里取2。

1.3 动态低阶固有频率拓扑优化目标函数

在满足结构静态刚度要求的前提下，结构动态特性设计的一个主要原则是避免有害的共振，即对结构的固有频率进行控制。以动态特性低阶模态固有频率最大为优化目标，通过提高车架的动态特性避免共振。为避免其中一个阶次的特征值达到最大时，其他阶次的频率可能降到较低的值，使几阶频率之间产生次序互换而导致的目标函数振荡问题，本文中将多个低阶模态频率均考虑到目标函数中，以保证频率交替时，目标函数仍保持光滑，由此运用平均频率[7]公式定义固有频率优化目标函数如下：

(2)

式中：wk为第k阶频率的权重系数；m为需要优化的阶次；λk为第k阶特征频率；λ0、∂为给定参数，用来调整目标函数。

1.4 静动态多目标拓扑优化目标函数

针对静动态车架结构的多目标拓扑优化问题，以车架的静态多工况刚度和动态低阶固有频率为优化子目标，以体积作为约束，通过拓扑优化计算得到同时满足刚度和频率要求的车架结构。多目标拓扑优化函数为

(3)

式中：ψmax和ψmin分别为频率目标函数的最大值和最小值；Λk为子目标权重值。

2 车架结构多目标拓扑优化

2.1 车架拓扑优化模型的建立

将车架的CAD模型结构进行适当的简化后，转化为CAE模型，完成车架有限元模型的建立。该矿用自卸车车架上的主要装备质量如表1所示，车架上的载荷通过MASS点进行模拟。

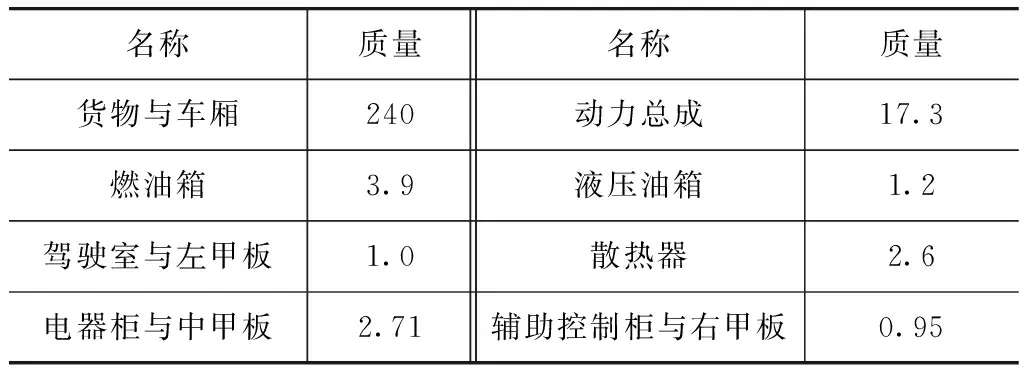
表1 自卸车主要装备件质量 t

在对车架进行拓扑优化前，将车架有限元模型划分为设计区域和非设计区域，非设计区域保留原车架模型，采用壳单元进行离散，而设计区域则采用实体单元进行填充，如图1(a)所示，车架拓扑优化模型如图1(b)所示。

实体单元只有平移自由度，壳单元既有平移自由度又有旋转自由度，为避免自由度不协调，采用rbe3单元将实体单元与壳单元进行连接。

2.2 边界条件

为获取悬架与车架连接处的随机载荷谱，依据多刚体动力学原理，借助ADAMS建立矿用自卸车多体动力学模型，如图2所示。

该矿用车采用油气悬架，依据《汽车工程手册》[8]，结合本悬架的结构特点，利用Matlab编程模拟悬架的刚度阻尼特性，如图3所示。

为了验证模型的准确性，对该自卸车进行了矿山路面的满载整车试验，试验道路为矿车实际作业场，如图4所示。试验车速分别为10,20和30km/h。

车速为30km/h时，车架与悬架连接点加速度的实车试验值与仿真值对比如图5所示。

表2为不同车速下悬架与车架铰接点加速度的平均值仿真结果与试验结果的对比。

W2#=0.6(0.6415,0.1279,0.7428,0.1056,0.0961)+0.4(0.0364,0.0509,0,0.0174,0)T=(0.3995,0.0971,0.4457,0.0703,0.0577)T

由表2可知，试验值与仿真值接近，平均误差在10%以内，从而验证了该整车动力学模型具有一定的准确性。提取车架与悬架处的随机载荷，其中后悬架与车架铰接点的载荷谱如图6所示。

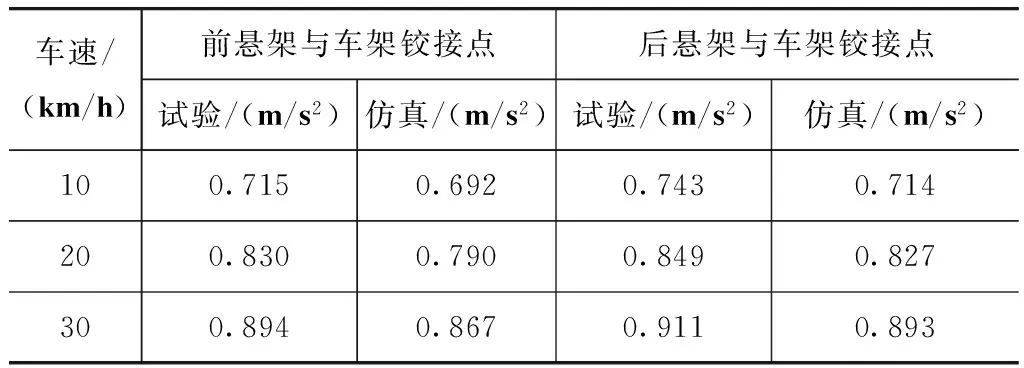
表2 悬架与车架铰接点平均加速度对比

2.3 子目标权重分配

层次分析法[9]将定性与定量分析相结合，基于严格的数学理论解决多目标求解问题。层次分析法对于因素权重的求解采用两两子目标相对比较的方式，形成配对比较矩阵。本文中所研究的车架静动态多目标拓扑优化问题具有7个子目标，即4个刚度子目标和3个频率子目标，定义其权重因子分别为α1、α2、α3、α4、α5、α6、α7，构成判断矩阵A=(αij)：

(4)

αij的取值是将每一个子目标作两两比较，将其之间的关系量化，主要以1、3、5、7、9为主，但在实际应用中，根据多目标优化项目的不同，可取其中间数值进行表示。判断矩阵集A为

(5)

将判断矩阵A归一化后得到B：

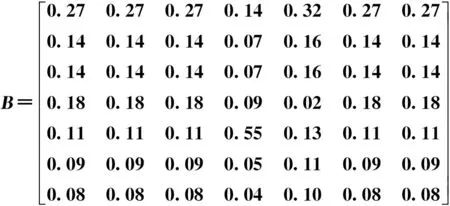
(6)

将矩阵B进行行向量相加获得行向量矩阵，规范化处理后得到排序向量W：

W=[0.250.130.130.140.180.090.08]

2.4 车架多目标拓扑优化的实现

Optistruct软件中只能采用线性加权法处理多目标拓扑优化问题，但该方法对于非凸优化问题，不能确保得到Pateto最优解，这里采用自定义函数来完成多目标的设置，以体积为约束，同时采用对称约束减少模拟的工况数，利用脱模约束使车架结构趋近于梁结构，完成车架结构的多目标拓扑优化。

3 优化结果分析

通过拓扑优化计算，最终得到同时满足刚度和频率要求的车架拓扑结构，如图7所示。由拓扑优化结果云图可以看到，在车架的中后部和靠前部位均形成了X型梁，该结构抗扭刚度非常高且占用空间少，结合车架上载重的分布(即240t的货物与车厢位于车架的中后部，17.3t的动力总成则装于车架的前部)，该拓扑优化结果合理。

图8为静态4种工况下(包括1个弯曲工况和3个扭转工况)应变能迭代历程，可以看出，在迭代过程中，4种工况下的应变能均有所降低。图9为前3阶固有频率优化迭代历程，可以看出，前3阶频率均有不同程度的提高，且未发生交替现象即避免了振荡的产生，静态刚度和低阶固有频率均得到提高，达到了优化的目的。

依据车架优化结果，结合车架实际使用情况(如车架后部要与后桥壳相连接且要保证不与其他部件发生干涉)，对车架进行再设计，新车架的有限元模型如图10所示。图11示出新车架与原车架结构的变化。优化前后车架的刚度和频率变化如表3所示。

由优化结果得到车架的刚度和固有频率均提高，下面研究对比新车架与经验设计下车架的疲劳寿命的变化。采用全局应力方法对车架进行疲劳寿命分析，车架材料为高强度钢，利用Msc.Fatigue提供的材料库，根据定义好的模块获得车架材料的S-N曲线，车架的载荷谱则由2.2节中随机路面下整车动力学仿真分析获得。对新车架与原车架施加相同的材料参数和载荷谱，获得疲劳寿命对比结果，如图12所示。车架的危险部位均出现在纵梁与尾梁连接处，由于此处为车架的主要承载部位且靠近后悬架，所以其寿命分布合理。由对比云图可以看出，新设计车架的最低疲劳寿命为3.62×106次，高于原车架的3.26×106次，且疲劳寿命相对较高的区域明显增加。

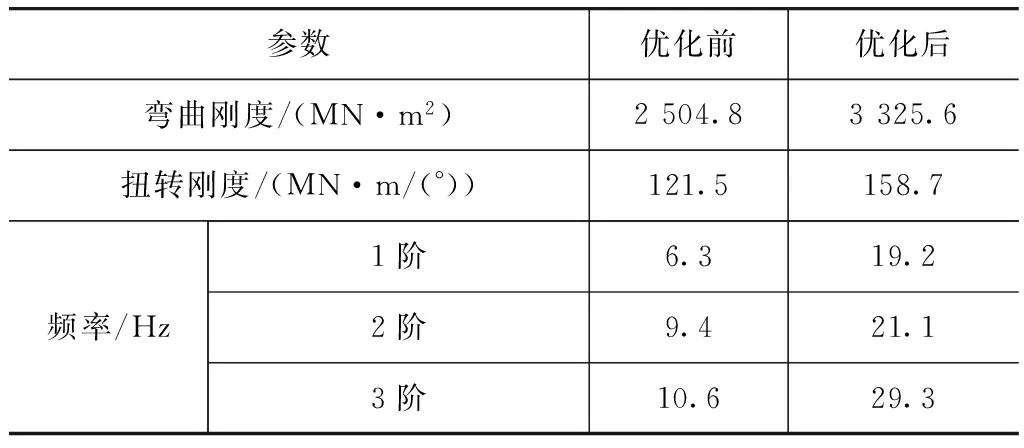
表3 车架优化前后刚度及固有频率对比

4 结论

(1) 同时考虑车架静态多工况刚度和动态多个低阶固有频率，采用层次分析法推导子目标的权重因子，在通过试验验证多体动力学模型可靠的基础上，借助多体动力学分析获得车架的边界条件，实现了静动态多目标下车架结构的拓扑优化。

(2) 优化结果显示，各工况下车架的应变能和低阶固有频率均有提高，且平均频率的考虑避免了低阶频率交替产生的目标函数振荡现象。

(3) 依据优化结果设计新的车架结构，采用全局应力法研究对比两车架的疲劳寿命，结果显示新车架的最低疲劳寿命高于原车架的最低疲劳寿命，使用寿命得到提高。

(4) 本文中对于车架结构的静动态多目标拓扑优化方法，同时从多个角度考虑了结构的实际工作状态，降低了单一工况、频率优化造成的设计风险，为工程应用中车架的优化设计提供了有效参考。

[1] Pedersen N L. Maximization of Eigenvalues Using Topology Optimization[J]. Structural and Multidisciplinary Optimization,2000,20:2-11.

[2] Rong J H, Xie Y M, Yang X Y. An Improved Method for Evolutionary Structural Optimiziation Against Buckling[J]. Computer & Structures,2001,79:253-263.

[3] 朱光谦.某SUV车架结构拓扑优化研究[D].秦皇岛:燕山大学,2010.

[4] 祝小元,方宗德,申闪闪.汽车悬架控制臂的多目标拓扑优化[J].汽车工程,2011,33(2):138-141.

[5] 范文杰,范子杰,苏瑞意.汽车车架结构多目标拓扑优化方法研究[J].中国机械工程,2008,19(12):1505-1508.

[6] 李好.基于变密度法的连续体结构拓扑优化方法研究[D].武汉:华中科技大学,2011.

[7] Ma Z D, Kikuchi N, Cheng H C. Topological Design for Vibrating Structures[J]. Comput. Methods Appl. Mech. Engrg.,1995,121:259-280.

[8] 张小虞,叶平,田炜,等.汽车工程手册[M].北京:人民交通出版社,2001.

[9] Saaty T L. The Analytic Hierarchy Process[M]. New York: Mc Graw-Hill,1980.

Static / Dynamic Multi-objective Topology Optimizationof the Frame Structure in a Mining Truck

Zang Xiaolei1, Gu Zhengqi1,2, Mi Chengji1, Wu Wenguang1, Jiang Jinxing1& Wang Yutao1

1.HunanUniversity,StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,Changsha410082;2.HunanUniversityofTechnology,Zhuzhou412007

To achieve static / dynamic multi-objective topology optimization for the frame structure of a mining truck in extreme adverse working conditions, a multi-objective topology optimization scheme for vehicle frame is proposed with static stiffness for multi-conditions and multi-low-order-frequencies as objective functions. A topology optimization model for frame structure is built based on variable density method, and the objective functions for multi-conditions stiffness topology optimization and vibration frequency optimization are determined by using compromise programming approach and mean frequency method respectively with their weighting factors selected by analytic hierarchy process. Topology optimization is performed, leading to the increases in both stiffness and low-order natural frequencies of frame. A comparative analysis on fatigue life is performed on both new frame after optimization and original one and the results show that after multi-objective topology optimization the fatigue life of frame is apparently increased with its operation performance improved.

frame structure; variable density method; analytic hierarchy process; multi-objective topology optimization

*国家863计划项目(2012AA041805)和湖南省科技重大专项计划项目(2009GK1002)资助。

原稿收到日期为2013年5月8日，修改稿收到日期为2013年10月2日。