基于高斯金字塔的图像运动估计算法

王 斌，何中市，伍 星，贾媛媛

重庆大学 计算机学院，重庆 400044

1 引言

在大部分图像数据应用领域里，为了获取高质量图片，常常要求获得具有高分辨率的图像，然而现实世界中，能够获取的多为低分辨率图像。因此由低分辨率图像重构高分辨率图像成为当前研究的重点，即超分辨率图像重构技术。图像运动估计的结果直接影响最终超分辨率图像的质量，是超分辨率图像重构过程中一个极其重要的环节。所谓运动估计就是估计同一个被观测物体在相邻两帧图像中的坐标差，即该对象在这两帧图像中的运动偏移矢量。然而运动估计的病态性（即可以使用不同运动矢量来描述同一副图像）导致运动估计成为数字图像处理领域中一大难题。

运动估计方法有多种，其中基于块匹配的运动估计[1-3]（BMA）算法由于其简单高效，额外开销小，易于硬件实现等优点，成为最常见的运动估计算法。块匹配算法依据某个衡量准则，通过在两幅图像之间进行块匹配，来寻找使得差异最小的度量，从而获得参数估计。现有的块匹配搜索算法有很多，如全搜索算法、三步搜索、四步搜索、菱形搜索法等。

全搜索算法：全搜索算法可以获得最佳结果。虽然它能够找到最优解，但其运算量大，不利于实时的应用。为减少运动搜索复杂度和运算量，研究人员相继提出了很多基于搜索模式的快速搜索算法，如三步搜索、四步搜索、菱形搜索等。

三步搜索算法[4]：三步搜索算法是一种快速搜索算法。三步搜索算法因其简单性和有效性被广泛使用，但容易陷入局部最优。

三步搜索、四步搜索都假定运动矢量是均匀分布，不符合实际情况。一些新的改进算法，充分考虑了真实序列的运动矢量分布特性，在改进搜索策略的同时提高搜索速度。如菱形搜素算法[5-6]拥有很好的匹配效果，且显著地减少了搜索点数，提高了运动估计速度。

菱形算法由于其较为优越的综合性能被MPEG国际标准采纳并收入验证模型，菱形搜索算法近来有许多改进算法的出现，比较出名的有十字形运动搜索算法[7]（NCS）。十字形搜索算法将菱形搜索算法的搜索模式改成了一个大的十字形搜索模式，使用十字模版搜索相对传统菱形搜索模式能减少搜索点数，但会使图像质量受到一定损伤。之后在原始十字形运动搜索算法的基础上又出现了一些新的改进算法，如改进的十字-菱形搜索法[8]、改进的十字菱形搜索算法INCDS[9]。这些算法虽然能较少搜索点数，但由于依赖于一些附加条件，使得算法的使用受限，如改进的十字菱形搜索算法INCDS需要预测搜索初始点，且需要复杂的附加算法确定算法的提前结束等。

同时也有一些学者提出了一些综合几个搜索策略的搜索算法，如一种综合搜索策略的快速运动估计算法[10]。

运动估计中的运动偏移量以不同的比例集中分布在中心附近区域，且在不同半径的搜索区域内大多数的运动偏移量分布在中心十字形区域上[11]，基于此本文提出了改进的小十字形算法INSCS，是在改进的十字形搜索的基础上，引入高斯分层思想。该算法相对于当前的一些新的且取得不错效果的算法（如上文提到的改进的十字形搜索算法、基于综合搜索策略的算法），无需引入附加条件，算法实现过程简单，有利于实时计算。实验结果显示：改进后的小十字形算法INSCS在保证图像质量的前提下，相比经典菱形搜索算法以及十字形搜索算法，搜索点数更少，搜索速度更快，且图像质量基本保持不变。

2 十字菱形搜索法简介

块匹配算法的搜索模版决定了其搜索速度，十字菱形搜索算法以大十字和小十字作为搜索模版，如图1所示，图1（a）是大十字形搜索模式，图1（b）是小十字形搜索模式。

十字形搜索算法的搜索过程大概可分为3步：

（1）先使用大十字模式搜索，搜索范围为大十字模式所包含的9个点，对这个9个点分别计算以这些点为中心的子块与被匹配块之间的平均绝对距离MAD。MAD最小的点可能出现的位置有3种：若该点为中心点，结束搜索；若该点位于内层的4个点之一，转入第（2）步；若该点位于最外层的4个点之一，转入第（3）步。

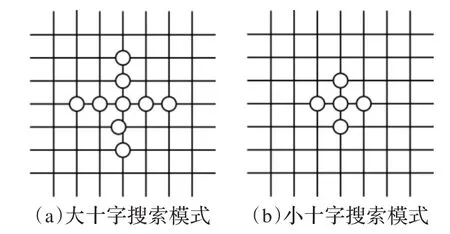
图1 十字菱形搜索模式

（2）如果MAD最小的点位于中心点的水平方向上，接着搜索该点上面和下面的两点，比较其MAD值，最小的MAD值对应的点即为最佳匹配点，搜索结束。如果该点位于中心点的竖直方向上，则比较其和左右两点的MAD值，值最小的位最佳匹配搜索点，搜索结束。

（3）以该点为中心扩展一个新的大十字，然后转入第（1）步。

本算法不仅兼顾到了运动矢量的中心偏移特性，又集中了“力量”搜索中心点水平和竖直两个方向上的点。初始步长为2，避免由于搜索过粗或过细而陷入局部最优，大十字的迭代适合运动范围较大的图像，并且可以在大十字搜索完成后，通过得到最佳点来减少搜索点数；小十字用来“查缺补漏”，用在最佳点位于其余几个方向上时。

3 基于高斯金字塔的小十字形搜索算法

为了进一步减少搜索点数，在传统十字形搜索算法的基础上，引入高斯金字塔思想。

3.1 图像金字塔

由一个原始图像经过降采样得到一幅下采样图像，再对下采样图像继续降采样，重复多次构成一组图像集合。如果形象的把这些图像摞起来就像一个金字塔，即图像金字塔，如图2所示。

图2 高斯金字塔分层结构

3.2 高斯金字塔

高斯金字塔是图像金字塔的一种，它在下采样之前，先使用高斯平滑滤波器[12]对原图像进行平滑。采用Gaussian金字塔对图像进行重采样，如果分辨率降低一半，那么运动偏移值也将降低为原来的1/2，且搜索范围也会减少，将大大提高搜索速度。构建图像Gaussian金字塔分两步计算：第一步对图像做高斯（Gaussian）平滑；第二步向下采样，借助亚采样可以获得一幅图像的一个缩略图，但如果需要减少一幅图像的尺寸，仅仅靠亚采样会丢失许多信息。根据采样定理，需要让所有小于最短波长的1/4采样而得到的精细结构能通过平滑滤波器来消除掉，这样才能获得一幅正确的采样图像。假设原图为M×N大小的图像，金字塔第l层图像的数字表达式，第l层是由l-1层Al-1经Gaussian窗口函数W卷积及下采样得到，公式如下：

其中 0≤i＜M/2l，0≤j＜N/2l，0≤l≤t（t＞0，为分解层数），窗口函数W的大小为(2s+1)×(2s+1)。

3.3 基于高斯金字塔的小十字形搜索算法

本文通过对十字形搜索算法的研究，总结十字形搜索算法可改进的方向，在引入高斯金字塔的思想上，提出了改进的小十字形搜索算法INSCS。这里的小十字搜索是指在搜索时只使用小十字搜索模式（图1（b））进行搜索，直到最小的MAD点出现在小十子模式中心点为止。为了进一步提高搜索效率，在这里引入了搜索的提前终止原则。关于提前终止判定阈值的确定[13]，文献采用全搜索法的实验结果表明，在采用像素16×16为块大小，匹配误差函数采用绝对误差和SAD的情况下，选取512作为零运动块预判阈值可以提高运动估计的速度，同时匹配效果并没有受到太大的影响。在这里直接使用512作为判断搜索是否终止的阈值。实验表明，在保持图像质量的前提下能显著提高搜索效率。

算法基本思路为：对原图像构建一个两层的高斯金字塔，下采样后的图像如图2的Level-2（这里图2中的K=2），大小为原图的1/4。由于下采样后图片的粒度比原图大1倍，这里将只使用小十字形搜索模式搜索，并引入提前终止原则，以此估计出参考图像与待匹配图像在Level-2层中的运动偏移。然后以此结果作为初始值，在Level-1（也即原始图像）中寻找最终运动估计值，由于下采样后，图像大小大大减少，因此能够有效降低了搜索范围，减少搜索时间。该算法的流程图如图3所示。

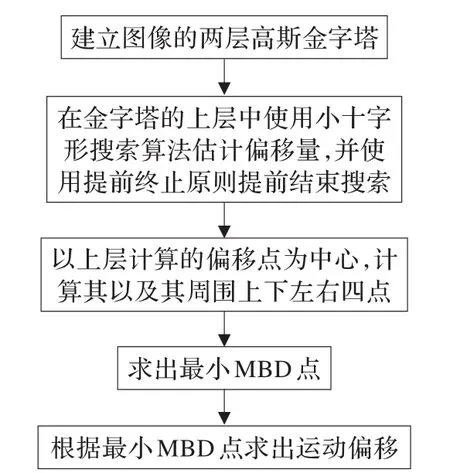
图3 本文算法流程图

算法过程可描述如下：

（1）对原图像进行高斯分层，本文将下采样因子设为2，分为两层。可参照图2，这里原图即为Level-1，下采样后的图为Level-2，Level-2为Level-1的1/4大小。

（2）先在Level-2中使用小十字形搜索算法，并使用提前终止原则，估计出参考图像与匹配图像间的运动偏移，这里使用PSNR（峰值信噪比）作为MBD的度量。PSNR计算如下：

其中n是每个采样值的比特数，在图像处理中通常n=8。MSE（Mean Square Error）为两帧图像间的平方误差，计算如下：

其中，r、c分别为图像的行列大小，pij为参考图像中的像素点，是过运动估计后，生成图像的像素点。如果Level-1即原图的运动估计的搜索窗口为15×15，那么在Level-2中，只需将其搜索窗口设为7×7，Level-2中的每一个7×7的窗口对应Level-2中的一个15×15的窗口。

（3）以（2）中估计出来的运动偏移，作为初始偏移值，然后在Level-1层即原图中，分别计算参考图像以及匹配图像以初始点，以及以初始点周围上、下、左、右4个点为中心的子块间的MAD（绝对平均值），MAD最小的点为最终被匹配块的中心点，以此算出运动偏移值。

4 实验结果分析

4.1 实验

为了证明本文算法的有效性，将INSCS算法（本文改进的小十字形搜索算法）与DS（菱形搜索）算法、NCS（十字搜索算法）以及AHSDS（自适应六边形和小菱形搜索算法）[14]在搜索点数、峰值信噪比，以及运行时间（为整个图像序列运行的Matlab的CPUtime）方面进行实验对比。算法运行环境为 Matlab R2011b；PC配置为2 GB内存，Intel Pentium Dual CPU E2180@2.00 GHz，Windows 7系统。

为了方便讨论算法的有效性，将实验分为两个部分：第一部分将算法应用于单张图片及其衍生图像上；第二部分将算法应用于标准图像集上。两组实验如下：

第一组实验，对单个图像即图4进行对比实验，具体操作为对图像4分别进行[-4，-2]，[-1，-1]平移操作，得到img1（原图）、img2、img3共3幅图像，在3幅图像上进行实验比较。

图4 单张图像偏移

第二组实验，选择5组典型的标准测试序列，序列格式为QCIF。第一组测试序列长度为61帧 Graden-gray 352×240Ras序列图像，其中Garden-gray序列主要是镜头的平移运动。第二组测试序列为33帧Caltrain序列图像，其中包含镜头平移以及内部对象的移动。第三组测试序列为60帧Football序列，主要包含内部对象的移动。第四组为75帧Susie序列，包含有局部物体运动。第五组为148帧Tennis序列，包含剧烈的场景运动。

在实验结果评价过程中，使用平均绝对距离MAD（Mean Absolute Distance）作为BDM度量标准。块的大小固定为16×16，搜索窗口为w=±7。最终的评价准则为：搜索点越少，搜索效率越高，峰值信噪比越大，估计的效果越好。

4.2 实验结果与分析

第一组实验结果见表1，可知与传统DS算法以及NCS相比，不论图像的运动偏差大（img2）或者小（img3），本文算法INSCS在保持PNSR性能下降很少的前提下，其搜索点方面的性能明显优于传统DS算法以及NDS算法；且运动偏差越大提高效果越明显。

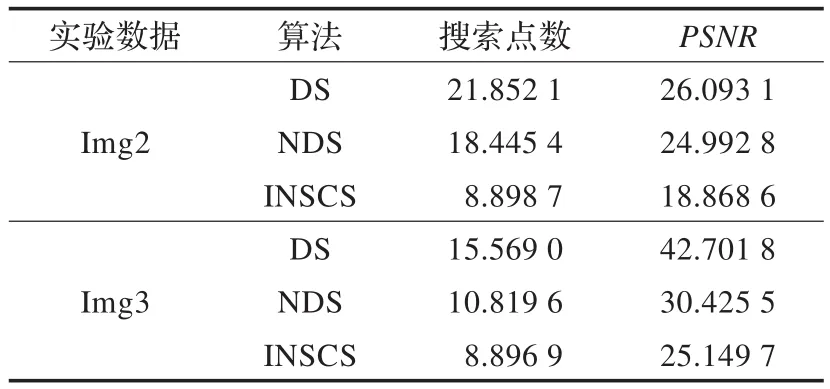
表1 单张图片实验结果

第二组实验，这里将实验分成两部分：第一部分，在每一组序列图像中，以彼此相隔2帧图像的图像对为参考对，即图像对为(i，i+2)，其中i代表序列中的第i帧图像，结果见表2，其中Caltrain-2表示帧间间隔为2的Caltrain图像序列，其余的类似。第二部分以彼此相隔4帧图像的图像对为参考对，即图像对为(i，i+4)，结果见表3，其中Caltrain-4表示帧间间隔为4的Caltrain图像序列，其余的类似。由表2可知，在第一部分中，本文算法INSCS在搜索点数方面相对传统DS算法以及NDS、AHSDS算法，搜索点个数最多减少128.24%、96.55%以及16.82%（表中的提高比例为本文算法相对于被比较算法的提高比例），而PNSR最多下降了8.91%、6.76%、4.05%。在第二部分中，见表3，搜索点个数最多减少168.74%、131.16%、23.91%，PNSR最多下降9.03%、7.43%、4.00%。同时由表4可知，本文算法在实际执行时间上也明显优于被比较的几种算法。

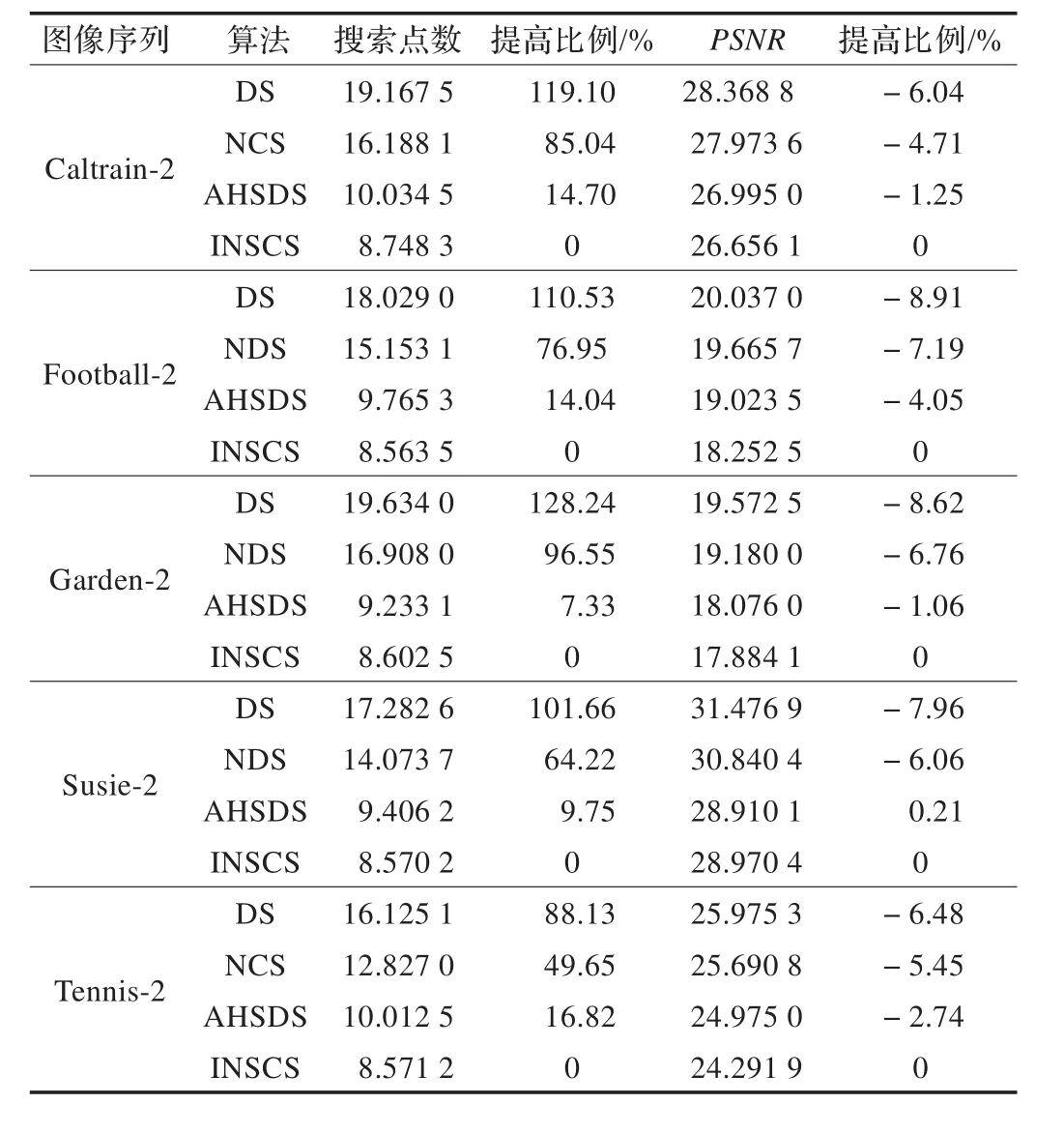
表2 第二组实验第一部分实验结果（图像序列帧间隔为2帧）

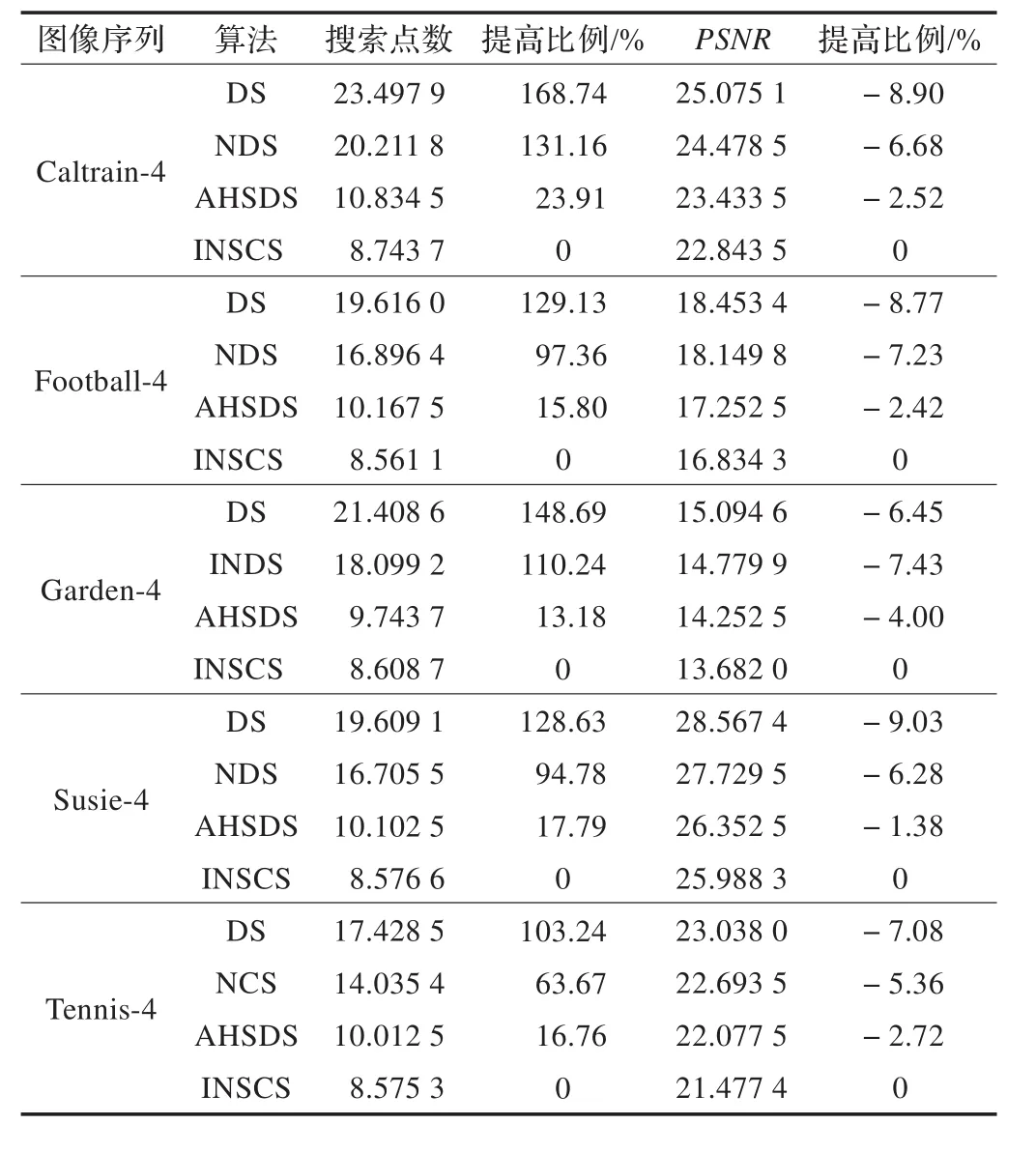
表3 第二组实验第二部分实验结果（图像序列帧间隔为4帧）

表4 第二组实验第二部分实验时间结果（图像序列帧间隔为4帧）

在算法实现方面，本文在引入高斯金字塔后只使用了小十字搜索模式进行搜索。相对传统DS算法的大小菱形模式，十字搜素算法的大小搜索模式，以及AHSDS算法的六边形模式和小菱形模式，在搜索模板的存储以及搜索点确定方面硬件消耗更少。而且相对于AHSDS算法需要较为复杂的运动强度预测估计来判断选择搜索模式，本文算法更为简洁，而且由于先使用高斯金字塔将搜索粒度放大，因此相对于AHSDS算法在正常粒度下的小菱形模式搜索，能够更加快速的定位。但是由于在搜索的第一步要建立高斯金字塔，因此在运动偏差很小的时候，未必能够取得最佳的效果。由表4可知，在Garden序列中（此序列主要包括小幅度平移），搜索时间不如AHDSD算法。这是由于当本身运动偏差很小的时候，先建立高斯金字塔的附加过程，反而减慢了搜索速度，而AHSDS算法在这种情况下能够直接通过小菱形搜索模式进行搜索，反而提高了搜索速度。

由上可知，总体而言，本文算法INSCS相对于传统DS算法以及NDS、AHSDS算法，在保持图像质量的前提下，其搜索点效率方面有明显的提升。而且在运动偏移较大的时候，提高更为显著（第二组实验第二部分效果好于第一部分）。

5 结论

通过对十字形搜索算法以及高斯金字塔算法的研究，提出了改进的小十字形搜索算法，将高斯金字塔分层的思想引入到十字形搜索算法中来估计图像运动偏差，并通过设定阈值提前终止搜索算法。在保持图像质量的前提下，本文算法明显提高了搜索效率，而且无需引入复杂的附加条件，算法实现简单，便于实时计算。但是关于如何更好地处理运动偏差很小的情况，将是后续研究的重点。

[1]胡喜华，刘卫忠，郑立新.运动估计块匹配算法的分析与研究[J].电视技术，2005（12）：4-6.

[2]吴通.基于H.264块匹配运动估计的研究[D].武汉：武汉理工大学，2008.

[3]Baby D V，Sumbramanian P，Karthikeyan C.Performance analysis of block matching algorithms for highly scalable video compression[C]//Proc of International Symposium on Ad Hoc and Ubiquitous Computing，2006.

[4]孙宁宁，樊超，许柯加，等.一种有效的三步运动估计算法[J].红外，2010，31（4）：37-41．

[5]Zhu S，Ma K.A new diamond search algorithm for fast block-matching motion estimation[J].IEEE Trans on Image Processing，2002，9（2）：287-290．

[6]Tham J Y，Ranganath S，Ranganath M.A novel unrestricted center-biased diamond search algorithm for block motion estimation[J].IEEE Transactions on Circuits and Sustems for Video Technology，1998，8（4）：369-377.

[7]赵跃华，雷茂惠，宋雪烨，等.一种十字形运动搜索算法[J].微计算机信息，2006，22（8）：1304-1310.

[8]刘海华，雷奕，谢长生.改进的十字-菱形运动估计搜索算法研究与实现[J].计算机应用研究，2007，24（8）：212-214.

[9]张万绪，吴佳丽，赵丽平，等.改进的十字菱形搜索算法INCDS[J].西北大学学报，2011，41（2）：226-230.

[10]王纯，孙中华，贾克斌.一种综合搜索策略的快速运动估计算法[J].计算机应用研究，2010，27（8）：2857-2860.

[11]Xie Chunlai，CheungChunho，Liu Weizhong.A novel adjustable multiple cross-hexagonal search algorithm for fast block motion estimation[J].Science A，2007，8（8）：1304-1310．

[12]张小洪，杨丹，刘亚威.基于Canny算子的改进型边缘检测算法[J].计算机工程与设计，2003，39（29）：113-115.

[13]Nie Yao，Ma Kaikuang.Adaptive rood pattern search for fast block-matching motion estimation[J].IEEE Trans on Image Processing，2001，11（12）：1442-1449.

[14]张小红，张东波.H.264块运动估计自适应快速搜索算法研究[J].计算机工程与应用，2013，49（6）：183-186.