改进PSO的飞机驾驶舱组合排序人机布局优化
2015-04-11余隋怀初建杰张婉玉赵明磊
刘 昕,余隋怀,初建杰,姚 澜,张婉玉,赵明磊
西北工业大学 现代设计与集成制造教育部重点实验室,西安 710072
1 引言
人机布局优化问题就是按照人机工程学原理,将待布物更合理地布置在有限空间内的优化问题。人机布局分为二维人机布局和三维人机布局,它们一般要求待布物之间、待布物与舱壁之间互不干涉,尽量提高空间利用率的同时,融入人机工程学的约束。
在飞行过程中飞行员必须保持注意力高度集中,目前我国飞机驾驶舱大多参考美俄标准,但我国飞行员工效尺寸却与美俄有很多不同,直接借鉴或套用相关研究结论,会导致我国飞行员驾驶舒适度差,进而引发飞行员过早疲劳,情况严重时会引起飞行事故。我国飞机驾驶舱的人机工效相关问题已引起关注,许多人机评价方式被提出[1-3],但缺乏符合我国飞行员工效尺寸的飞机驾驶舱人机布局优化算法。
粒子群算法,也称粒子群优化算法(Particle Swarm Optimization,PSO),是近年发展起来的一种新的仿生智能算法,由Eberhart和Kenned于1995年提出,源于对鸟群捕食的行为研究[4]。粒子群算法以其实现容易,精度高,收敛快,鲁棒性好等优点引起了学术界的重视,并且在求解工程复杂布局问题中展示了其优越性。文献[5]中,粒子群算法首次被用于解决球状舱体的圆形待布物的二维优化布局,并于次年首次用于球状舱体的方体待布物的二维优化布局中[6]。2011年,Sadan Kulturel-Konak首次将粒子群成功运用于解决不规则图形的布局优化问题[7]。2013年,遗传算法被首次应用于民用飞机驾驶舱布局优化中。粒子群算法由于没有遗传算法的“变异”(Mutation)和“交叉”(Crossover)操作,因而比遗传算法规则更为简单[8]。本文首次将粒子群算法应用于飞机驾驶舱的三维人机布局优化当中,并首次将基于非线性递减惯性权重的改进粒子群算法引入飞机驾驶舱人机布局优化中。另外,与近年来应用于其他舱体布局优化的算法,如蚁群算法[9],以及应用于民用飞机驾驶舱的遗传算法进行了优化效果的对比。由于飞机驾驶舱人机布局较为庞大复杂,融入组合排序方法,提出一种符合我国飞行员标准的飞机驾驶舱人机布局的优化方法,该优化方法能够充分利用飞机宝贵而又狭小的工作空间,提高空间的利用率和促进各设备之间的良好搭配,保障飞行员长时间驾驶的舒适度,减少过早疲劳的概率,减少误操作。
2 飞机驾驶舱人机布局优化原理与实现过程
组合排序方法是在空间上,将相同的物体或相关操作加以组合,在时间上,将相同或相关的操作进行合并[10],然后,按重要性对不同组合进行排序的过程。是使系统庞大、流程繁复的工作更有条理、更具次序地进行的重要途径和方法。飞机驾驶舱人机布局待布物较多,不同待布物之间的相互关系和相对位置错综复杂,引入组合排序方法梳理待布物间的相互重要关系,将具有操纵关联性的待布物进行组合排序,相互协调配合,有次序地进行分析。
粒子群算法对待诸如可微分、时间连续等优化函数没有任何特别的要求,所以其通用性极强,尤其对于高度非线性、多变量、不连续的目标函数,更能凸显其优势[11]。粒子群算法没有太多需要调节的参数,因此容易实现,它通过追随当前搜索到的最优值来寻找全局最优[12]。由于飞机驾驶舱待布物较多,意味着约束条件较多,使用粒子群算法寻找目标函数最优解,可避免陷入局部最优,计算过程也相对容易掌握。另外,采用相对于线性递减惯性权重,普遍具有优越性的非线性递减的动态惯性权重系数对粒子群进行改进,平衡粒子群算法的全局搜索能力和局部改良能力的同时,使人机布局最优解更为精确。
以下是飞机驾驶舱人机布局优化的实现过程:(1)确定飞机驾驶舱待布物的组合排序;(2)建立飞机驾驶舱人机布局优化的目标函数;(3)对最重要且还没确定位置的待布物进行人机布局约束;(4)按组合排序,依次优化待布物;(5)重复第二步骤;(6)分析完最后一个待布物,相互妥协调整后,得到布局优化的最优方案。
3 基于改进粒子群算法的飞机驾驶舱人机布局优化模型构建
飞机驾驶舱人机布局优化是以飞机驾驶舱的人-机-环境系统为优化对象,在宝贵且有限的空间内,以改善飞行员的劳动条件和提高飞行员的舒适度为核心,以飞行员安全、健康、舒适、高效驾驶为宗旨,提高空间设备的利用率和各设备之间的良好搭配为目标,使整个飞机驾驶舱总体布局达到最优。
3.1 确定飞机驾驶舱待布物的组合排序

图1 待布物组合排序层次目标树
飞机驾驶舱控制器较多,需要根据功能重要性和操作顺序进行组合排序,使飞机驾驶舱的人机布局优化分析井然有序。由于待布物要根据同组的其他待布物进行定位参考,根据布局需要,不同组合中的待布物可能会有一定交叉。另外,组合与组合之间需要排序,组合内的待布物也需要排序。如图1所示,首先,根据不同待布物的性能将待布物主要分为操纵区、显示区、供电通信系统、安全消防系统和座椅5项组合。其次,通过b名具有飞机驾驶经验的评判员对待布物及其组合进行排序,并使用Kendall’s W对b组数据进行一致性检验。最后,得出待布物及其组合排序。根据不同的飞机机型,相同待布物的重要性不同,专家需对众多待布物需要进行不同的组合排序。
3.2 目标函数的确定
飞机驾驶舱布置优化中,设备控制器众多,相对位置关系复杂,需要几项目标在允许区域范围内达到最优,即实现多目标优化。以往的单目标优化算法往往不能解决多目标优化问题,一般的做法是将多目标优化问题转化为单目标优化问题,常用方法有目标规划法、理想点法、权重系数变换法等[13]。本文采用权重系数变换法,如式所示:


3.3 飞机驾驶舱待布空间人机布局约束
可视域约束视角是确定被看物尺寸范围两端点光线射入眼球的交线角度,视角大小与观察距离及被看物体上两端点的直线距离有关,可用下式表示:

式中,a为观察一个待布物或多个待布物时形成的人的视角,(xi,yi,zi)和 (xj,yj,zj)分别是形成人视角的待布物上的两点,人单眼的水平视角最大可达156°,双眼的水平视角最大可达188°。人两眼重合视域为124°,单眼舒适视域为60°。
可达域约束根据飞行员的实际工作情况,参照GJB4856-2003,采用坐姿人体尺寸标准,对我国飞行员的可达域进行分析。

如图2所示,式(3)和(4)中,人眼位于坐标原点0,S为我国飞行员的肩宽,E为飞行员眼睛到肩关节在y轴方向上的水平距离,L为飞行员眼睛到肩关节的垂直距离,T为飞行员的肩外侧到肩关节在x轴方向上的水平距离。不同百分位的飞行员取值不同。
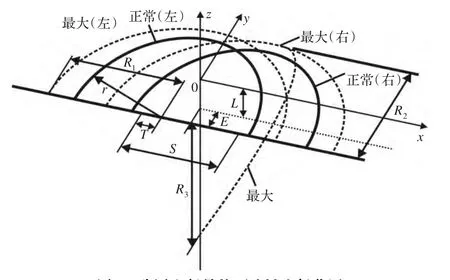
图2 我国飞行员的可达域坐标范围
待布物互不干涉约束条件:

式中,(xi,yi,zi)是待布物i的形心坐标,ai、bi、ci分别是待布物i的长、宽和高;(xj,yj,zj)是待布物j的形心坐标,aj、bj、cj分别是待布物j的长、宽和高。
3.4 基于改进粒子群算法的人机布局优化求解思路
假设在一个n维的目标搜索空间中,有m个粒子组成一个群落以一定的速度飞行,xi=(xi1,xi2,…,xin),为粒子i在n维空间里搜索的位置,将xi代入目标函数可计算出其适应度值,根据适应度值的大小衡量xi的优劣。vi=(vi1,vi2,…,vin)为粒子i的当前飞行速度。第i个粒子迄今为止搜索到的个体最优位置记为pbesti=(pbesti1,pbesti2,…,pbestin),整个粒子群迄今为止搜索到的全局最优位置记为gbesti=(gbest1,gbest2,…,gbestn)。
粒子飞行速度和位置根据个体的飞行经验和群体的飞行经验进行动态调整,其速度和位置的更新方程为[14]:

其中i=1,2,…,m;j=1,2,…,n;c1和c2为加速因子或称学习因子,用来调节粒子飞向个体最优值pbest和全局最优值gbest的最大步长[15],一般取值为2;r1、r2为[0,1]的随机数[16-17]。
但基本粒子群算法的速度缺乏有效的控制,不具备较强的局部搜索能力,为有效控制粒子群的飞行速度,改变基本粒子群算法的收敛性能,Shi和Eberhart于1998年引入惯性权重系数w,对基本粒子群算法进行改善,如式(8)所示:
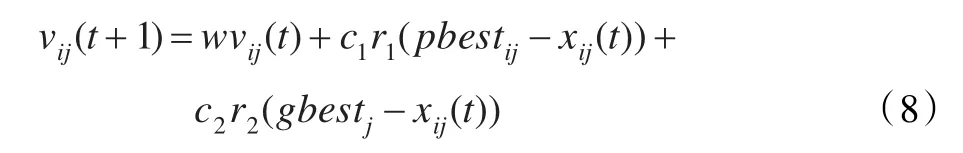
较大的w可增强全局搜索能力,较小的w可提高局部搜索能力,因此调整惯性权重,使之产生变化可平衡基本粒子群算法的全局搜索能力和局部改良能力。根据不同的权重变化规律,可产生不同的粒子群改进方法,常用的有线性权重递减,即让权重值从最大值wmax线性减小到wmin。但在一般情况下,非线性递减的惯性权重更加灵活,并且相对于线性递减惯性权重可在一定程度上提高算法的效率和精度。由于本文涉及的飞机驾驶舱操纵器系统庞大,造型复杂,待布物多,均采用具有普遍优越性的改进对驾驶舱布局进行优化,能节省计算机的工作量。
采用非线性权重系数,即自适应权重系数对基本粒子群进行改进,其表达式为:

其中,wmax、wmin分别表示w的最大值和最小值,f表示粒子当前的目标函数,favg和fmin分别表示当前所有粒子的平均目标值和最小目标值。因此,惯性权重可随粒子的目标函数值自动进行调整,当各粒子的目标值趋于一致或趋于局部最优时,惯性权重变大,而各粒子的目标值比较分散时,惯性权重减小,同时对于目标函数优于平均目标值的粒子,其对应的惯性权重因子较小,从而保留了该粒子,使该粒子往较好的搜索区靠拢。
改进粒子群算法实现飞机驾驶舱人机布局优化步骤如下:(1)对粒子群初始化,随机产生服从均匀分布的粒子的位置和速度向量;(2)计算每个粒子的适应度函数值,并将适应度函数值最优的粒子设为全局最优值gbest;(3)根据式(7)、式(8)和式(9)更新粒子的速度和位置信息;(4)将每个粒子的当前适应函数值分别和其经历过的个体最优值pbesti和全局最优值gbest的适应度函数值比较,如果当前适应度函数值优于pbesti或gbest的适应度函数值,则将当前粒子位置设为pbesti或gbest。(5)重复第(2)步到第(4)步,迭代n次直至待布物坐标数值不再更新为止。
4 实例应用
以某轻型商用飞机的人机布局优化为例。
确定飞机驾驶舱待布物的组合排序顺序,并使用Kendall’s W进行一致性检验,请现役且具有丰富经验的飞行员4人,参与飞机驾驶舱有关的国家级重大项目的研究员2人,年龄均在25~35岁,对待布物的组合1,2,…,k,按重要性,由重到轻的优化顺序进行排序,如表1所示。
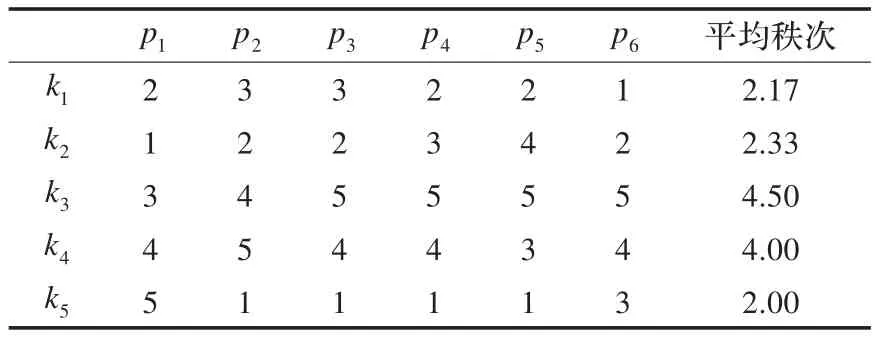
表1 6位专家排序与排序的平均秩次
采用Kendall协调系数W检验分析,得Kendall’sW=0.539,χ2=12.933,,则,即表1数据具有一致性。表1是专家经过第二轮排序所得的数据,第一轮排序由于不具有一致性而无效。
同理,经过专家们多轮排序,布置该飞机驾驶舱待布物大致的组合排序顺序确定如下:k13,k11,k12,k21,k24,k15,k14,k16,k23,k22,k44,k43,k41,k42,k32,k31。由于部分系统待布物较多,在具体操作过程中,也可根据需要调整部分顺序。

为了操作和维修的方便,在有的设备之间,设备与舱体结构之间,往往要预留一定的距离,从人机工效来说有一个最适宜的距离,但并非所有待布物能直接取值最适宜距离,每个待布物都必须兼顾整体布局。f(x)描述了在此方面的评价,f(x)越小越好。利用n维最小欧氏距离方法,并融合与远距离的设备形成的视角越小越好,将目标函数f(x)描述为:其中,式(4)和式(5)为式(10)的约束函数。在式(10)中,(xi,yi,zi)是设备i上点的坐标,(xj,yj,zj)是设备j上点的坐标,(xk,yk,zk)是设备k上点的坐标,设备j一般与设备i相邻,要求位置不干涉,或是和设备i操纵过程相联系,即与设备i为一个组合,但是排序后于设备i,与其具有一定距离要求;oij为考虑人机功效要求的设备i、j之间的最佳距离;设备k与设备i根据操纵需要,要求在一定视角范围内。
已知设备k多功能显示器形心坐标为(263.3,655,-232),设备j1混合比控制杆前推最远端点坐标为(255,383,-669),设备j2油门杆前推最远端点坐标为(230,352,-676),设备j3航空智能电子地图导航系统面板形心坐标为(221,480,-515),求解设备i襟翼的形心坐标的最优值。根据飞行员握拳时的尺寸、襟翼形心坐标离油门杆和混合比控制杆在3个坐标方向上的最小距离应至少为30 mm,才能在使用时互不干扰。根据导航系统面板的尺寸和操纵器一般人类工效学要求[18],其形心到襟翼形心的垂直距离应不少于120 mm,水平距离不少于60 mm。在使用襟翼时,要求能够观察多功能显示器,因此尽量使襟翼与多功能显示器形成的视角越小越好。另外,根据专家调查法与层次分析法分析得:=0.360,=0.360,=0.270,=0.315,=0.315,=0.270,=0.180,=0.180=0.360,w4=0.450,使用基本粒子群算法与改进粒子群算法,遗传算法和蚁群算法分别进行优化,基本粒子群算法学习因子取值2,惯性权重取值0.9,粒子数取值50;改进粒子群算法学习因子取值2,自适应权重最大值取值0.9,最小值取值0.6,粒子数取值50;遗传算法种群数取值50,交配概率取值0.6,变异概率取值0.1;蚂蚁数取值50,如图3~6所示,遗传算法的迭代次数较多,到153代以后变化才不大,而蚁群算法进化到22代以后却陷入了局部最优,基本粒子群算法和改进粒子群算法收敛效率最高,效果也最佳,并且由于改进粒子群算法所得最小值更小更精确,因此改进粒子群算法略优于基本粒子群算法,最后得襟翼形心坐标最优值如表2所示,该坐标在我国飞行员可达域舒适范围之内,且设备互不干涉。另外,点火电门的优化,如图7所示,最优坐标为(-204.568,625.851,-308.672),该坐标也在约束范围之内。

图3 求解襟翼形心坐标最优
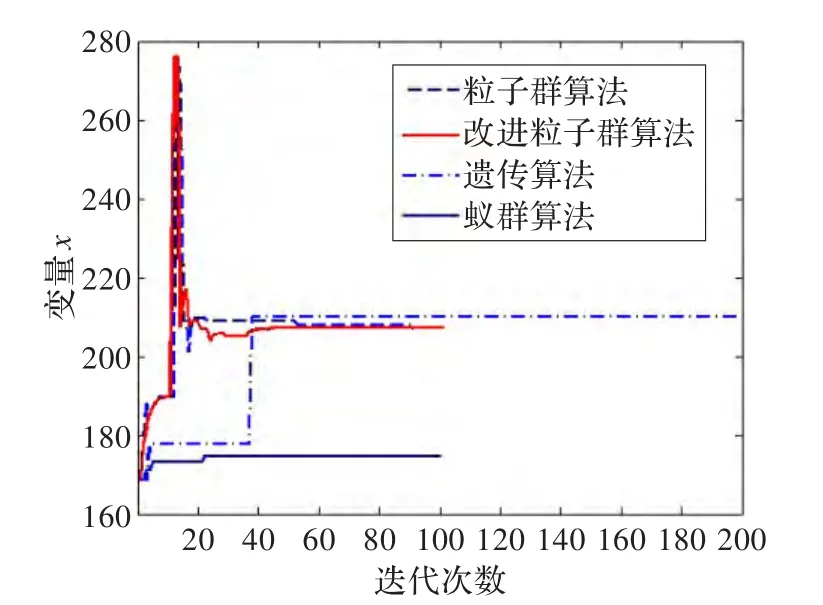
图4 变量x随迭代次数变化曲线

图5 变量y随迭代次数变化曲线

图6 变量z随迭代次数变化曲线

表2 4种优化算法最优解与目标函数最小值

图7 求解点火开关形心坐标最优
5 JACK模拟验证与布局优化方案评价
采用JACK6.1软件模拟飞行员飞行时的操作流程,分别建立第99百分位、第50百分位和第1百分位的我国飞行员模型,分别模拟飞行员对飞机驾驶舱原始布局和经过改进粒子群优化的驾驶舱布局进行操作,比较在两种布局空间内完成同样两组流程时飞行员疲劳恢复程度,完成流程A到流程B,最后到流程C的一系列动作。其中:
流程A发动机预热→座椅安全带和肩式安全带→油箱选择开关→燃油泵→混合比→襟翼→GPS调定→油门杆→开启信号灯→松开刹车→油门杆最大→升降舵操纵→收襟翼。
流程B模拟飞行中油门、混合比、驾驶杆、升降舵和襟翼等的一系列动作,历时1 h。
流程C油门杆→燃油泵→襟翼→信号灯→油门→点火开关。
从表3中可看出,经过对总流程的测试,使用优化后的布局,飞行员疲劳恢复时间明显小于原布局,由此可知,优化后的布局使飞行员使用更加舒适、省力。
如图8所示,通过JACK对最优方案分析,待布物在合理的可视域和可达域范围内,且使用舒适度处于较高水平。

图8 JACK可视域、可达域和舒适度分析
经过JACK对两个方案进行对比分析,验证了粒子群算法不仅可以有效应用于球状舱体的二维布局设计,通过与组合排序方法的结合,还能有效解决飞机驾驶舱的三维人机布局问题。
6 结论
在飞机设计规划初期,合理优化驾驶舱布局,能大幅度降低飞机制造成本。飞机驾驶舱空间有限,合理且高效地利用宝贵空间,又能保证飞行员安全舒适、省力地驾驶,具有切实意义。由于飞机驾驶舱操纵器系统庞大,待布物多,待布物所处环境和待布物造型都较为复杂,将组合排序方法融入改进粒子群算法,克服单一粒子群算法的局限性,对飞机驾驶舱空间布局有次序地进行了深入分析,提出了符合我国飞行员人机工程学原理的布局优化方法。根据驾驶舱的一般布局原则,确立的驾驶舱人机布局优化的目标函数为高度非线性函数,使用一般的优化方法容易陷入局部最优或运算效率较低,使用粒子群算法可调参数少,同时为了改善基础粒子群算法精度,进而引入自适应权重系数改进的粒子群算法。通过与基本粒子群算法,遗传算法和蚁群算法的对比,突出了改进粒子群算法在解决飞机驾驶舱人机布局优化问题的优越性,最后经过JACK分析进行验证,该优化方法结果符合我国飞行员人机特性,表明本文优化方法可以有效地解决飞机驾驶舱的三维人机布局问题。
[1]刘启越.民用飞机驾驶舱人机工效评价方法研究[D].南京:南京航空航天大学,2013.
[2]冯青,余隋怀,初建杰,等.基于AHP灰色理论的飞机驾驶舱内环境设计评价[J].航空制造技术,2012(17):72-75.
[3]李银霞,袁修干.飞机驾驶舱显控系统工效学评价技术研究综述[J].人类工效学,2007,13(2):63-65.
[4]钱锋.粒子群算法及其工业应用[M].北京:科学出版社,2013.
[5]刘飞,孙明,李宁,等.粒子群算法及其在布局优化中的应用[J].计算机工程与应用,2004,40(12):71-73.
[6]孙明,刘飞,孙德宝,等.旋转卫星舱内长方体群的布局[J].计算机工程与应用,2004,40(34):92-94.
[7]Kulturel-Konak S,Konak A.A new relaxed flexible bay structure representation and particle swarm optimization for the unequal area facility layout problem[J].Engineering Optimization,2011,43(12):1263-1287.
[8]钮松.面向民机驾驶舱人机工效设计的布局优化研究[D].南京:南京航空航天大学,2013.
[9]范文,余隋怀,王文军,等.蚁群算法求解人机布局优化问题[J].机械科学与技术,2013(7).
[10]赵敏,史晓凌,段海波.TRIZ入门及实践[M].北京:科学出版社,2009.
[11]中国文本库.PSO算法使用简介[EB/OL].[2014-08-01].http://www.chinadmd.com/file/wersxxozattvwooopp6pcixe_1.html.
[12]张利彪.基于粒子群优化算法的研究[D].长春:吉林大学,2004.
[13]周发模.粒子群算法及其在机舱布置优化的应用研究[D].武汉:武汉理工大学,2009.
[14]张丽平.粒子群优化算法的理论及实践[D].杭州:浙江大学,2005.
[15]赵晶.量子行为粒子群优化算法及其应用中的若干问题研究[D].江苏无锡:江南大学,2013.
[16]Zhao F,Li G,Yang C,et al.A human-computer cooperative particle swarm optimization based immune algorithm for layout design[J].Neurocomputing,2014,132:68-78.
[17]Jolai F,Tavakkoli-Moghaddam R,Taghammad M.A multiobjective particle swarm optimisation algorithm for unequal sized dynamic facility layout problem with pickup/dropoff locations[J].International Journal of Production Research,2012,50(15):4279-4293.
[18]国家技术监督局.GB/T14775-93操纵器一般人类工效学要求[S].1994.
