基于改进支持向量机的快速稳健代理模型研究

刘玉琳 ，陈文亮 ，鲍益东 ，丁力平

1.安徽工业大学 数理学院，安徽 马鞍山 243032

2.南京航空航天大学 机电学院，南京 210016

1 引言

“代理模型”即通过建立输入参数和输出响应的函数关系，将未知的物理黑箱问题转化为显示的数学描述。代理模型技术可以通过少量的计算，构建能够反映系统物理实质的数学模型，解决了传统的优化算法和启发式优化算法的技术瓶颈。基于代理模型的优化方法是求解大规模非线性问题最有希望的方法之一[1]，鉴于其高效性，广泛应用于工程优化领域。如果能够高效建立稳健的代理模型，很多大规模工程问题便可以迎刃而解。

主流的代理模型技术，如多项式响应面、Kringing插值、神经网络、径向基插值等[2-5]，多数建立在经验风险最小化准则之上，导致丧失了推广能力，难以反映研究目标的实质和特性。支持向量机（Support Vector Machine，SVM）是由Vapnik[6]提出的一种基于小样本统计学习理论和结构风险最小化的建模方法，具有坚实的理论基础，较好的泛化能力及强大的非线性和高维处理能力。Suykens等[7]提出最小二乘支持向量机（Least Squares Support Vector Machine，LS-SVM），选择误差平方和作为损失函数，用等式约束代替不等式约束，将求解过程转变成一组等式方程，避免了求解耗时的二次规划（Quadratic Programming，QP）问题，使求解速度加快。LS-SVM在工程领域得到了广泛的应用[8-10]，但LS-SVM在简化计算的同时，也丧失了解的稀疏性和稳健性等优点。

在实际工程中，样本采集是一个容易受环境条件和人为操作等不确定因素影响的过程。因此，训练样本中难免会混入少量和大多数正常样本差异显著的异常样本。LS-SVM对异常样本的存在十分敏感，通常存在一个或几个异常样本就会很大程度地破坏模型的特性。为了增强LS-SVM的稳健性，Suykens等人提出了加权LS-SVM（Weighted Least Squares Support Vector Machine，WLS-SVM）算法来减少异常样本对回归机的负面影响[11]；包鑫对Suykens等人提出了加权算法进行了改进[12]；Zhang和Guo提出重加权算法，通过对样本进行重加权，逐步减少异常样本的影响，修正回归机的估计值[13]；赵永平等提出了基于滚动窗思想的最小二乘支持向量机稳健模型构建方法[14]；张淑宁等人提出了鲁棒最小二乘支持向量回归机算法，通过引入鲁棒学习来获得鲁棒估计[15]；Shim等人采用模糊聚类来实现最小二乘支持向量机稳健回归[16]。上述加权方法仅根据回归误差确定权值，采用“误差大相应的权值小，误差小相应的权值大”原则，没有考虑到用于建模的样本的分布不均匀性。但由于采用自适应的建模方法，建模数据信息会重复出现在某些局部区域，用于建模的样本具有冗余的特性。因此，模型会对某些特殊点（如“拐点”等）的表达不明显，削弱了某些特殊点对回归模型的贡献，回归模型易产生过拟合现象。并且上述加权方法本质均假设回归误差ek服从均值为0的正态分布。如果样本点集合中没有异常样本存在，该假设是正确的。然而，由于异常样本分布的影响，特别是异常样本点数量较多时，假设样本误差ek均值为0是不稳健的。

针对WLS-SVM传统加权方法易产生过度拟合及未考虑到回归误差分布特性问题，本文提出基于数学期望为med{ei}的正态分布概率密度函数确定权值方法。在此基础上，提出了迭代加权最小二乘支持向量机快速递推算法，利用矩阵关系进行迭代递推计算，减少计算量，节约迭代最小二乘支持向量机训练时间。

2 改进加权最小二乘支持向量机

2.1 加权最小二乘支持向量机

为了增强LS-SVM的稳健性，给定一个由l个样本数据组成的训练集{xi，yi}，xi∈Rn，yi∈R，i=1，2，…，l。在LS-SVM算法的基础上对误差变量ei进行加权，得到最优化问题：

其中w∈是权值向量，非线性映射Ф(x)：Rn→是将输入数据映射到高维特征空间的函数，误差变量ei∈R，偏置值b∈R，γ＞0为惩罚系数，vi∈R为加权系数，用于调节各样本点在模型中所起的作用。式（1）的最优化问题可变换到对偶空间加以解决，得到Lagrange函数：

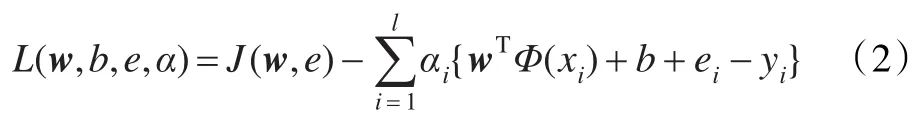
其中Lagrange乘子αi∈R。对各变量求偏导，并令它们等于0。

消去变量w和e，可得线性方程组：

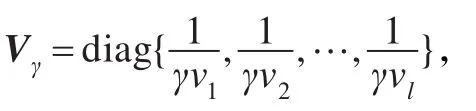
其中α、b为线性方程组（4）的解。

2.2 基于正态分布概率密度函数确定权值

根据稳健统计理论，采用基于中位数的统计量比基于均值的统计量具有更好的稳健性。为了使权值更能反映样本回归误差的分布特性，增强回归模型的稳健性，假设回归误差ei服从均值为med{ei}的正态分布，采用的权函数为：

其中med代表中位数。

正态分布概率密度函数中σ参数决定了正态曲线的形状：σ越小，分布越集中，曲线越陡峭；σ越大，分布越分散，曲线越扁平。考虑回归误差的统计特征，应遵循如下取值规则：如回归误差的分布较分散，则各样本点应赋予离散程度较大的权值，σ取值应偏小；如回归误差的分布较紧密，则各样本点应赋予离散程度较小的权值，σ的取值应偏大。

与已有加权方法相比，基于正态分布概率密度函数的加权方法削弱了样本冗余数据造成的“过度拟合”。在权值计算方面，两种方法的不同如图1所示。已有方法是回归误差绝对值越小，其权值越大。本文提出的加权方法对回归误差位于中间的样本赋予最大的权值，而误差远离误差中位数的样本赋予小权值。本文提出的加权法更侧重于自适应建模方法中训练样本的非均匀分布实际特性，并且采用回归误差的中值作为计算加权值的衡量标准，增强了算法的稳健性。

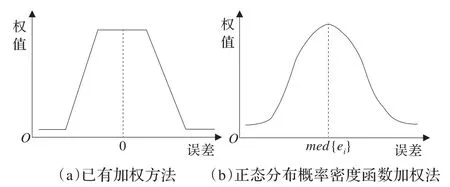
图1 两种加权方法对比示意图

2.3 迭代加权最小二乘支持向量机快速递推算法

迭代加权最小二乘支持向量机的每次迭代过程都需要重新训练一次，即重新求解线性方程组（4），因此将耗费较多的运算时间。针对该问题，从数值计算的角度给出一种迭代加权最小二乘支持向量机的快速递推算法。为了方便推导，将加权最小二乘支持向量机的对偶问题改写成如下形式：

定义1（Sherman-Morrison-Woodbury公式）给定一个可逆矩阵 A，列向量u1和u2，假设，则有以下公式成立：

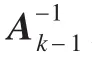
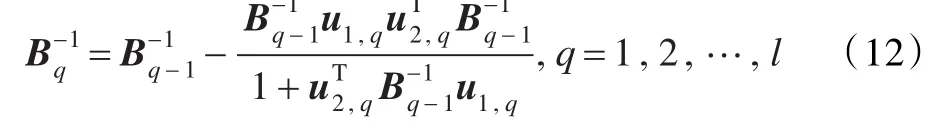
基于上述推导，迭代加权最小二乘支持向量机快速递推算法过程如图2所示。

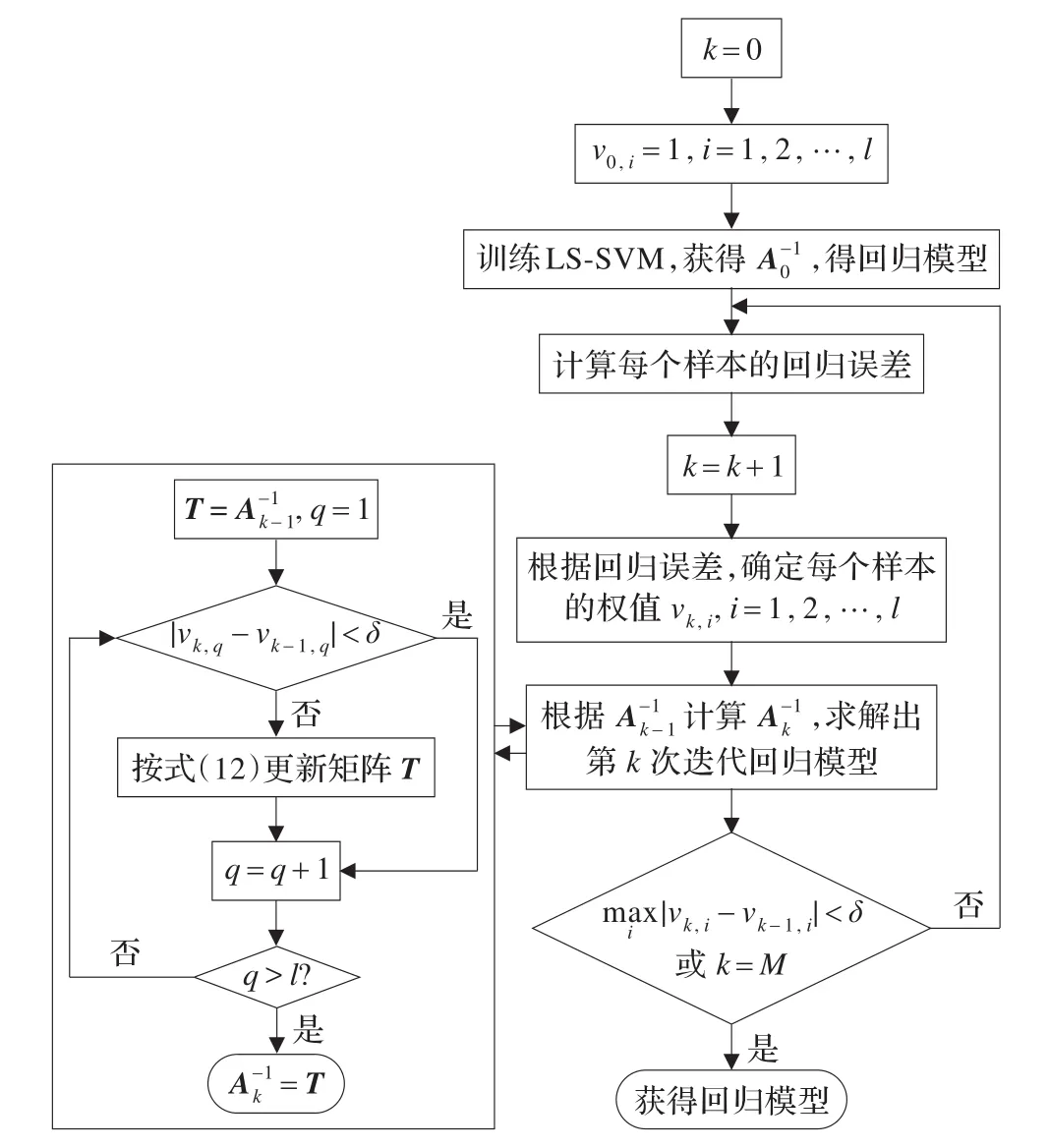
图2 迭代加权最小二乘支持向量机快速递推算法流程图

3 数值实例仿真实验

为了验证上述算法的可行性、有效性，采用一维非线性函数f(x)作为数值例子进行仿真实验。

训练样本由两部分组成，一部分是正常样本，由f(x)函数附加服从正态分布的随机噪声ξ～N(0，0.08)产生，另一部分是异常样本，由人为添加一些异常样本点构成，共66个训练样本点，其中异常样本点5个。为了模拟自适应建模方法中的建模数据信息会在某些局部区域具有冗余的特性，假定采样样本点在区间x∈[0.3，0.6]较密集，而在区间x∈[0，0.3]和x∈[0.6，1]较稀疏。

仿真实验中，支持向量机核函数取为径向基核函数。LS-SVM得到的回归结果，基于Suykens加权方法的传统WLS-SVM得到的回归结果，基于正态分布概率密度函数加权方法(σ=0.5)的改进WLS-SVM得到的回归结果分别如图3、图4、图5所示。

可看出，在训练样本存在异常样本点干扰的情况下，WLS-SVM的确比LS-SVM具有更好的拟合效果；并且在数据点密集处，基于Suykens加权方法的传统WLS-SVM和基于正态分布概率密度函数加权方法的改进WLS-SVM都取得了较好的拟合效果；而在数据点稀疏区域，本文提出的改进WLS-SVM则具有更好的拟合效果。

测试样本由不加噪声扰动的函数f(x)产生，并且设置与训练样本不同的采样间隔，确保测试样本与训练样本的独立性。表1为3种方法建模的预测误差分析结果。

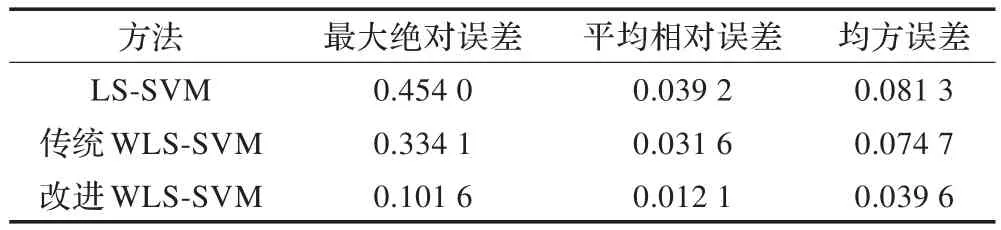
表1 预测误差统计分析结果

从数值仿真实验结果来看，针对自适应代理模型建模过程中样本点冗余、分布不均现象，传统加权方法侧重密集区域样本点而忽略其他样本时，会产生过度拟合。而本文提出的改进加权方法可有效地解决这类问题，进一步提高代理模型的回归精度，增强代理模型的稳健性。

为了考察快速递推算法的有效性，根据提出的基于正态分布概率密度函数加权方法，在Matlab 7.0环境下编写和运行了未加速的迭代加权最小二乘支持向量机算法及其快速递推算法。针对3个训练样本集，样本点总数分别为66、100、132，异常样本点数量分别为5、15、33，即3个训练样本集中异常样本的比例分别为7.5%、15%、25%，均在 Pentium®Dual-Core CPU 2.80 GHz，2.00 GB内存电脑配置下进行实验，训练时间的相关结果如表2所示。

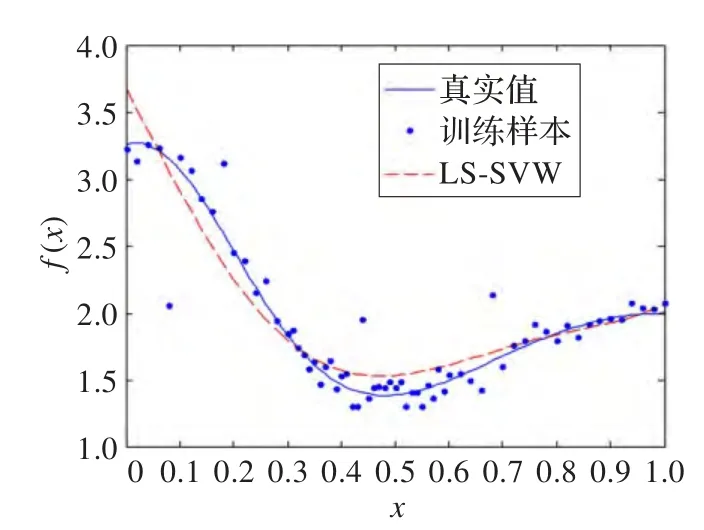
图3 LS-SVM方法回归结果

图4 传统WLS-SVM方法回归结果

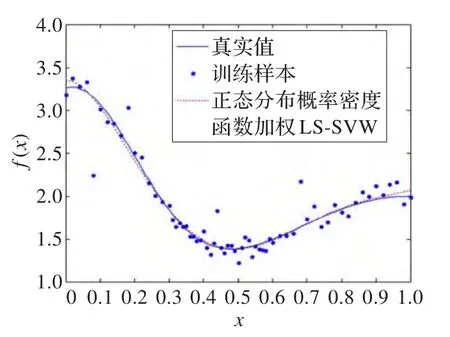
图5 改进WLS-SVM方法回归结果

表2 仿真样本点集训练时间对比

从训练时间来看，加速迭代加权最小二乘支持向量机算法远远少于未加速算法，可以节省大量的训练时间，这使得基于迭代加权的支持向量机稳健模型构建具备了时间效率上的可行性：不需要增加过多的训练时间就可以大幅提高代理模型对异常样本点的容忍度，获得更加稳健的预测结果。

4 结论

（1）正态分布概率密度函数加权法更侧重于自适应建模方法中训练样本的非均匀分布实际特性，削弱了样本冗余数据造成的“过度拟合”，并且采用回归误差的中值作为计算加权值的衡量标准，增强了算法的稳健性。

（2）迭代加权最小二乘支持向量机快速递推算法，根据Sherman-Morrison-Woodbury公式，利用矩阵关系进行前后两迭代步的矩阵求逆递推计算，避免了重新求解线性方程组，减少了计算量，节约了迭代加权最小二乘支持向量机训练时间。

（3）通过非线性函数数值算例的仿真实验，验证了本文提出的方法的可行性和有效性，提高了代理模型的预测精度，增强了代理模型的稳健性，缩短了稳健代理模型的建模时间。

[1]李光耀.板料冲压成形工艺与模具设计制造中的若干前沿技术[J].机械工程学报，2010，46（10）：31-35.

[2]Naceur H，Ben-Elechi S.Response surface methodology for the rapid design of aluminum sheet metal forming parameters[J].Materials and Design，2008，29：781-790.

[3]Jakumeit J，Herdy M，Nitsche M.Parameter optimization of the sheet metal forming process using an iterative parallel Kringing algorithm[J].Structural and Multidisciplinary Optimization，2005，29（6）：498-507.

[4]Zhang Yanqin.Research on method of sheet blank design based on ANN[J].Forming&Stamping Technology，2009，34（6）：62-64.

[5]Fang H，Horstemeyer M F.Global response approximation with radial basis functions[J].Journal of Engineering Optimization，2006，38（4）：407-424.

[6]Vapnik V N.Statistical learning theory[M].New York：John Wiley，1998.

[7]Suykens J A K，Vandewalle J.Least squares support vector machine classifiers[J].Neural Processing Letters，1999，9（3）：293-300.

[8]Suykens J A K，Vandewalle J.Optimal control by least squares support vector machines[J].Neural Networks，2001（14）：23-35.

[9]陈爱军.最小二乘支持向量机及其在工业过程建模中的应用[D].杭州：浙江大学，2006.

[10]王久崇，樊晓光，盛晟，等.改进的蜂群LS-SVM故障预测[J].空军工程大学学报：自然科学版，2013，14（1）：16-20.

[11]Suykens J A K，Brabanter J D，Lukas L，et al.Weighted least squares support vector machines：robustness and sparse approximation[J].Neurocomputing，2002，48（1）：85-105.

[12]包鑫，戴连奎.加权最小二乘支持向量机稳健化迭代算法及其在光谱分析中的应用[J].化学学报，2009，67（10）：1081-1086.

[13]Zhang J S，Guo G.Reweighted robust support vector regression method[J].Chinese Journal of Computers，2005，28（7）：1171-1178.

[14]赵永平，孙建国.基于滚动窗法最小二乘支持向量机的稳健预测模型[J].模式识别与人工智能，2008，21（1）：1-5

[15]张淑宁.基于鲁棒学习的最小二乘支持向量机及其应用[J].控制与决策，2010，25（8）：1169-1175.

[16]Shim J，Hwang C，Nau S.Robust LS-SVM regression using fuzzyC-means clustering[J].Advances in Natural Computer Science，2006，42（21）：157-166.