基于三阶段法的植被高度反演算法在植被稀疏区域的研究
2015-04-11宋桂萍蔡元妃
宋桂萍,蔡元妃
(河海大学 文天学院,安徽 马鞍山 243000)
1 引言
极化干涉SAR是一门综合的将干涉相位信息和极化信息高效的融合为一体的技术.该技术具有极化SAR对目标散射体的具体结构敏感的能力以及具有干涉SAR对目标散射体的空间结构敏感的特性[1].因此极化干涉SAR可以区分处于同一分辨单元内的不同散射机制相位中心,为提取地表植被垂直结构参数提供可能而成为当前研究的焦点问题,也是目前国家比较关心的重大问题.
随着近几年的发展,极化干涉SAR朝着多领域,多角度,多方向的发展,总的来说目前极化干涉SAR植被参数反演方法有这么几种方法:DEM差法[2]、三阶段法[3]、基于ESPRIT方法[4-5]和基于样本相关矩阵的最大似然估计算法[6].其中三阶段法是比较经典的算法之一.该算法的主要思想是通过最小均方差方法使预测植被模型和观测值参数之差最小化来求解植被的六种参数.然而三阶段法在植被稀疏区域应用的效果不佳或者说是不理想,甚至是无法反演出植被高度,本文通过欧空局提供的polSARpro软件中极化干涉SAR数据模拟模块模拟数据来表明该算法存在的一定的局限性和缺陷,需要进一步的对经典的三阶段法进行研究和改进,以此能够进一步的提高植被高度反演精度.于是本文先是阐述了三阶段法的基本原理,然后系统研究了三阶段法在植被稀疏区域的应用,指出该算法的局限性和存在问题,最后通过模拟数据验证了三阶段法在植被稀疏区域的局限性以及详细的分析了存在局限性的原因.
2 三阶段法的基本原理
最初提出三阶段法的学者是Cloude等人[3],并且将此方法用于极化干涉SAR植被高度反演中去.三阶段法基本原理是在最初的地体随机散射模型更加完善的基础上,采用数学上的几何方法反演植被高度,由此可以把该过程分成这么几步,即最小二乘直线拟合、最大植被偏差去除、植被高度和消光系数估算等[7-8].具体的过程如下:
(1)计算不同极化状态所对应的极化干涉复相干系数γHH,γHV,γVV,γHH-VV,γHH+VV或者 γopt1,γopt2,γopt3等.
(2)在复平面内将第一步骤中所计算出来的几种不同极化干涉复相干系数进行最小二乘直线拟合,如图1-1所示在复平面内就拟合为一条直线.该直线的有效长度依赖于所采用数据的基线、频率以及研究区域植被的密度等,延长该直线与单位圆相交可以得到两个相交点,这两个相交点所对应的相位分别覬1和覬2.
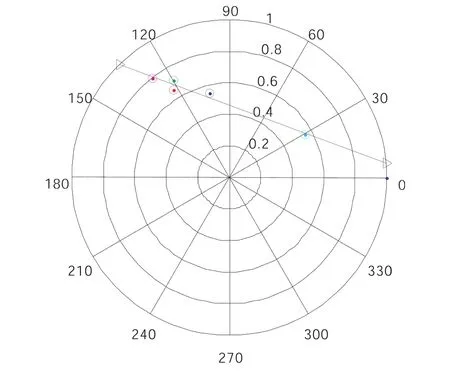
图1-1 最小二乘直线拟合图
(3)根据最大植被偏差去除准则判断出每个分辨单元内对应于地面的散射相位.具体的方法过程就是先计算出各个不同极化通道分别所对应的地体幅度比值,然后在这几个地体幅度比值中找出最小值,并计算出与两交点的相位距离,以距离最远的相交点作为地面散射相位.
(4)通过公式1-1可以反演出植被高度和消光系数.通常选择HV通道的极化干涉复相干系数值来进行计算,因为该极化通道对植被体散射比较敏感,最后就可以计算出体散射模型的相干系数值与其两者之间的差值.在这个过程中通过更新消光系数和植被高度候选值可以得到这个差值最小的结果.
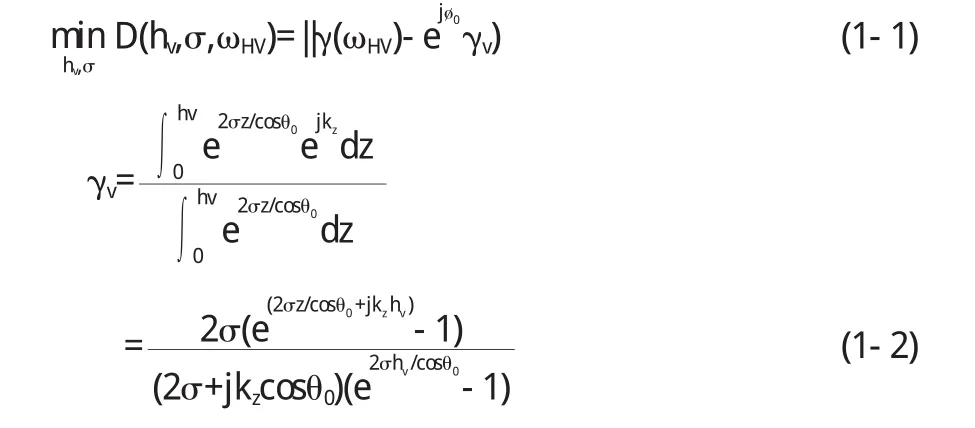
其中hv,σ分别代表植被高度和消光系数.
3 基于三阶段法的植被高度反演算法在植被稀疏区域的局限性
经典的三阶段法在植被稀疏区域反演植被高度由于不同极化方式的相干性比较接近或者比较相似,于是在此基础上最小二乘拟合估计出的地面散射相位误差较大,这就会对后面进行植被高度反演带来影响,或者是某些区域完全反演不出来.
为了说明三阶段法的局限性,于是在实验中分别采用三组模拟数据[9],这三组模拟数据除了植被密度不同,是由小到大,其他参数都是一样的.第一组数据植被密度是200stems/Ha,第二组数据植被密度是250stems/Ha,第三组数据植被密度是300stems/Ha.文中是利用欧空局提供的polSARpro软件里面极化干涉SAR干涉数据模拟模块进行数据模拟的,一般参数设置为平台高度3000米,垂直基线1米,水平基线10米,入射角度38度,距离向分辨率1.06米,方位向分辨率1.5米,植被高度为16米,植被类型是阔叶林.
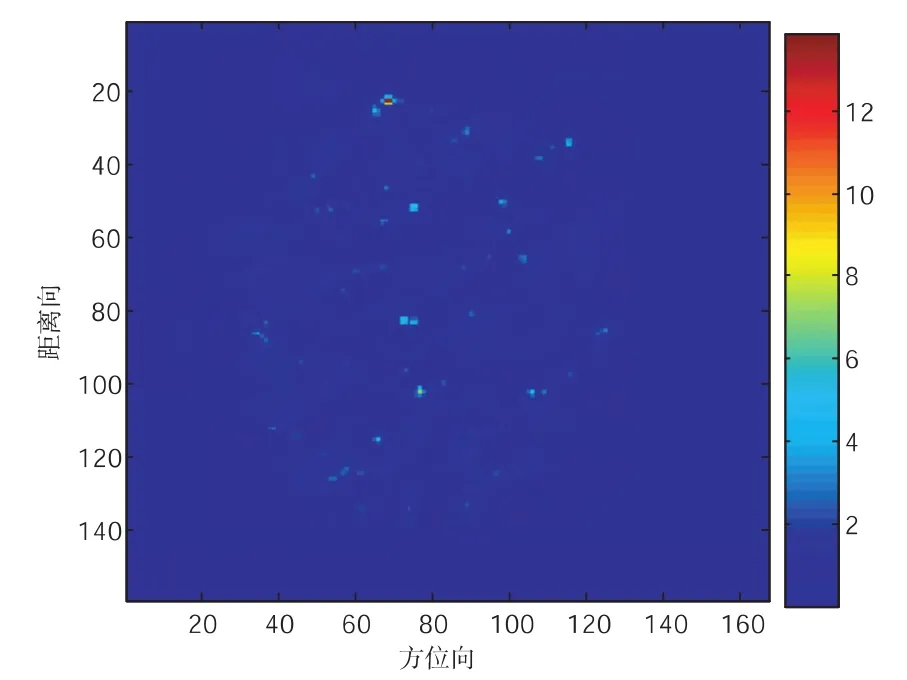
图1-2 主影像功率图
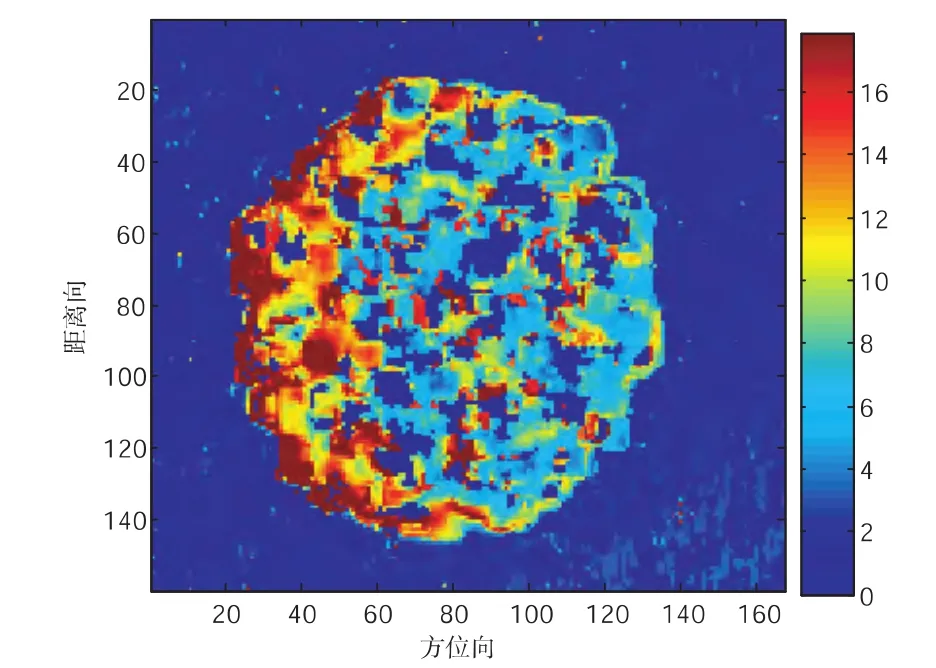
图1-3 三阶段法反演的植被高度图
第一组模拟数据的主影像图如图1-2所示,植被是中间圆形区域表示的,并且植被密度是一定的,分布均匀,其他区域是没有被植被覆盖的裸露地面.
图1-3所示的三阶段法反演的植被高度图,从图中可以看出反演的结果比较差,效果不是很好,甚至在有些地方三阶段法没有办法反演出植被高度.分析其原因可以有两点:第一点是由于在植被比较稀疏区域,在复平面内用不同极化的极化干涉复相干系数进行最小二乘拟合时,他们的相位中心都集中在一起,比较相近,最终使得拟合的误差较大,如图1-4所示.由此使得其估计出的地面散射相位误差比较大;第二点跟地面散射信号强弱有关,相对于植被密集的区域,在植被稀疏区域,地面散射信号比较强,这就会使得植被稀疏区域的地体幅度比值比较高.正是由于这两点原因会导致最终三阶段法植被高度反演精度严重偏低.
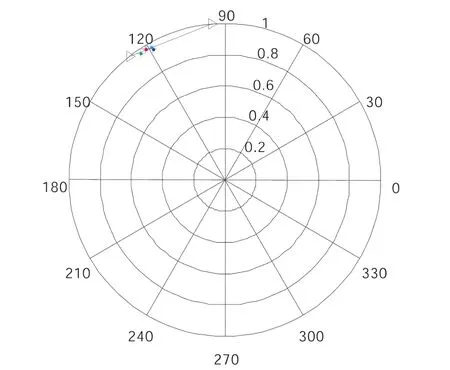
图1-4 最小二乘直线拟合图
图1-5所示的是第二组模拟数据的反演的植被高度图.
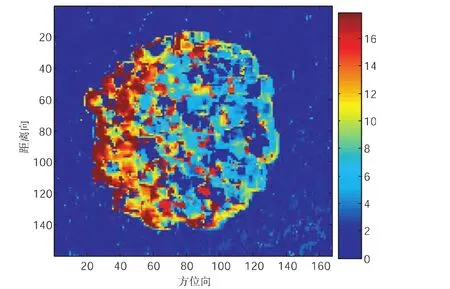
图1-5 三阶段法反演的植被高度图
从图1-6可以看出,第二组数据拟合出的最小二直线拟合图相对于第一组数据拟合的图来说,相位中心有所分散,但是还是有限的,因此地面散射相位估计精度不高,从而导致图1-5所示的三阶段法反演的植被精度不高,甚至在某些区域无法反演出植被高度,只是在植被密集的区域反演的植被高度效果比较好,反演的精度有所提高.
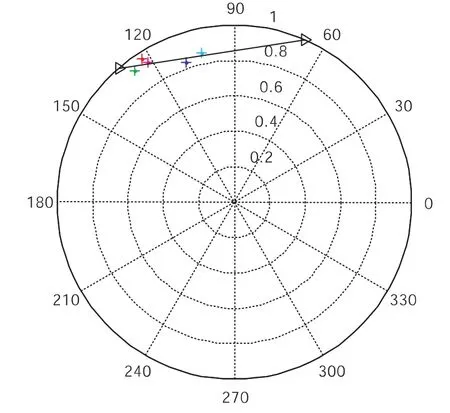
图1-6 最小二乘直线拟合图
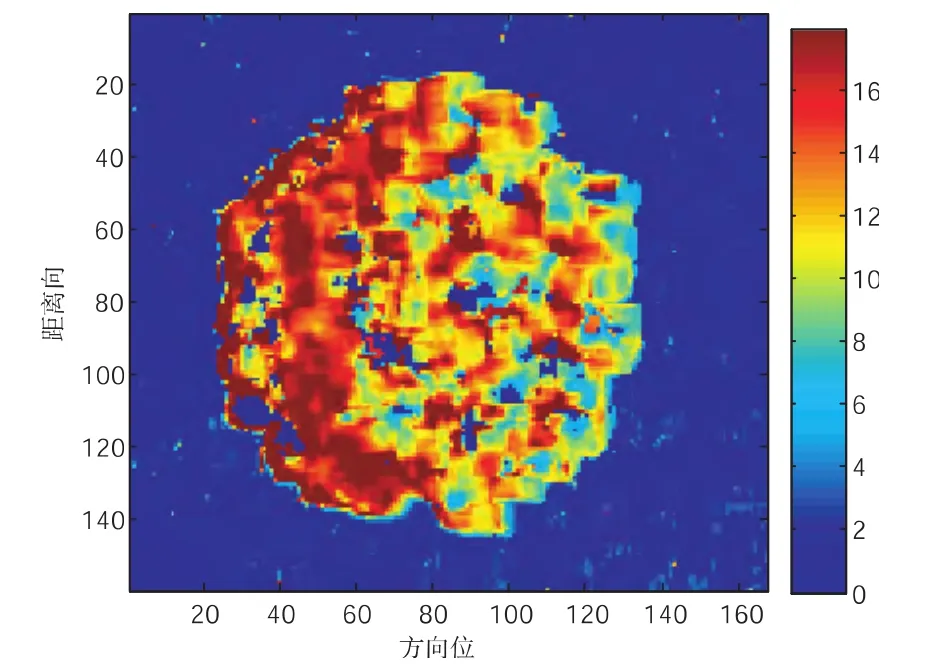
图1-7 三阶段法反演的植被高度图
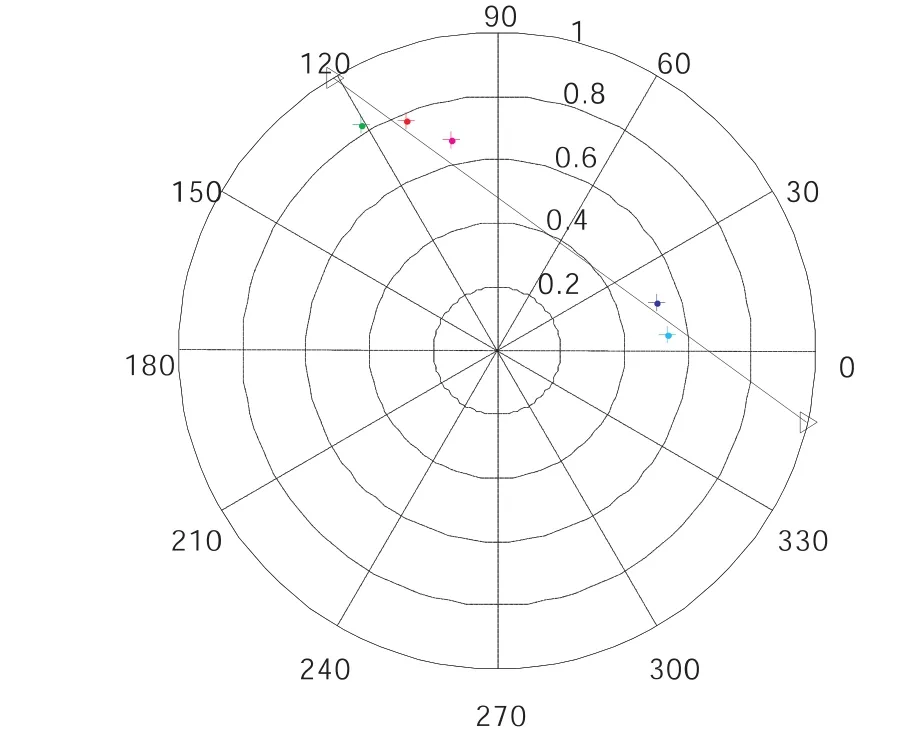
图1-8 最小二乘直线拟合图
第三组模拟的植被数据相对比较密集,模拟的植被密度比较大.图1-7所示的是三阶段法反演的植被高度图,从图中可以清楚地看出植被高度反演的比较好,分布匀称,植被边缘反演的效果尤其的显著,在反演精度上有较大的提高.从拟合图中可以看出在复平面内拟合的相位中心位置分布比较分散,分布区域也比较大,使得最终估算出的地面散射相位相对来说比较准确;从反演的结果看出,相比较前两组数据,三阶段法估计的地面散射相位精度有所提高,从而使得三阶段法反演的植被高度效果比较好,可靠性比较高.因此三阶段法在植被密集区域反演的植被高度效果要比植被稀疏区域.
4 结论
三阶段法在极化干涉SAR植被高度反演算法中是比较经典的算法之一,也是目前极化干涉SAR植被高度反演算法中用的比较多的方法之一.该算法利用数学中几何方法来反演植被高度,简化了运算的复杂性以及运算的过程,节省了算法运算的时间.但是该方法只有在植被密集的区域或者说是地体幅度比值比较低的情况下,其反演植被的效果比较好,比较明显,然而在植被稀疏的区域,由于地体幅度比值比较高使得不同极化复相干系数拟合计算出的地面散射相位中心不准,导致反演的精度低,反演的植被高度不均匀,甚至是有些区域无法反演出植被高度.因此,如何提高和改进三阶段算法在植被稀疏区域植被高度反演的精度将是下一步要研究的重点内容.
〔1〕李廷伟,梁甸农,朱矩波.极化SAR干涉森林高度反演综述[J].遥感信息,2009(3):95-101.
〔2〕S.R.Cloude,K.P.Papathanassiou.PolarimetricSAR Interferometry[J].IEEETransactionsonGeoscienceand RemoteSensing,1998,36(5):1551-1565.
〔3〕F.Garestier,P.C.Dubois-Fernandez,I.Champion.ForestHeightInversionUsingHigh-ResolutionP-Band PolInSARData [J].IEEETransactionsonGeoscience andRemoteSensing,2008,46(11):3544-3559.
〔4〕H.Yamada,Y.Yamaguchi,R.Members.Polarimetric SAR InterferometryforForestAnalysisBasedonthe ESPRIT Algorithm [J]. IEICE Transaction on Electronics,2001,E84C(12):1917-1924.
〔5〕谈璐璐,杨立波,杨汝良.基于ESPRIT算法的极化干涉SAR植被高度反演研究[J].测绘学报,2011,40(3):296-300.
〔6〕M.TABB,T.FLYNN,R.CARANDE.Full MaximumLikelihoodInversionofPolInSARScattering Models [C].ProceedingsofIEEE Geoscience and RemoteSensingSymposium2004.Alaska:IEEE,2004:1232-1235.
〔7〕CloudeS.R.,PapathanassiouK.P.A3-StageInversion Process for Polarimetric SAR Interferometry [C].ProceedingsofEuropeanSARConferenceEUSAR2002,2002,Germany,June2002:297-282.
〔8〕CloudeS.R.,PapathanassiouK.P.Three-stageInversion ProcessforPolarimetricSARInterferometry[J].IEEProc.RadarSonarNavigation,2003,150(3):125-134.
〔9〕SimardM.3DGlobalVegetationMap[OL].http://lidarradar.jpl.nasa.gov/,2011.
