压缩编码的上下文树构造算法
2015-04-10付敏戴祖旭王道蓬
付敏,戴祖旭,王道蓬
1 武汉工程大学理学院,湖北 武汉 430502;2 华中科技大学图像识别与人工智能研究所多谱图像信息处理国防重点实验室,湖北 武汉 430074
压缩编码的上下文树构造算法
付敏1,2,戴祖旭1,王道蓬2
1 武汉工程大学理学院,湖北 武汉 430502;2 华中科技大学图像识别与人工智能研究所多谱图像信息处理国防重点实验室,湖北 武汉 430074
上下文树是构造无算压缩算法的一种重要基础,作为信息处理过程分析随机序列统计特性的常用数据结构,随机序列中的符号来自于某个固定的符号集合.上下文树一般是一棵n元树,其中n大于1,但是树是一种占用计算机内存较多的数据结构,因此提出了基于压缩编码的上下文树构造算法,根据符号的一阶统计特性对符号做二进制的压缩编码,用二元树代替n(n>2)元树,在相同内存的存储空间下,可以大大增加树的高度.计算机数值实验表明基于压缩编码的上下树构造对子串做出了更大长度的相关性检测,并且提高了数据分析的精度.
上下文树;n元树;压缩编码
0 引言
信息处理技术的飞速发展使得算法应用越来越为广泛,在图像处理[1],路径搜索优化[2-3]以及工程应用等领域,数学形态学越来越重要.作为其中的一种重要的数据结构,上下文树是信息处理过程中分析随机序列统计特性的常用工具.利用上下文树获取序列中字符串[4-5]的频率分布,可以构造高效的数据压缩算法[6-7],通过上下文树分析文本或生物DNA序列中符号的相关性,可以准确实现文档或DNA序列的自动分段[8-9].同时,上下文树也是研究可变长Markov链的主要数学工具,用于随机序列发生器设计[10-11].
随机序列中的符号来自于某个固定的符号集合,比如英文文档包括26个字母,DNA序列由A、C、G、T组成,它们分别代表组成DNA的四种核苷酸一腺嘌呤、胞嘧啶、鸟嘌呤和胸腺嘧啶.因此上下文树一般是一棵n元树,其中n大于1.树是一种占用计算机内存较多的数据结构,系统内存容量会直接影响树的高度,而树高决定了分析过程中序列子字符串的长度,会直接影响符号串统计特性的精度.
本文提出了基于压缩编码的上下文树构造算法,根据符号的一阶统计特性对符号做二进制的压缩编码,用二元树代替n(n>2)元树,在相同内存的存储空间下,可以大大增加树的高度,对子串做更大长度的相关性检测,提高分析的精度.
1 上下文树
设A={a1,a2,…,an}是一个符号集合,随机序列x=x-Nx-N+1…x-1x0x1…xMxi∈A,i∈I从序列x中任取一点,比如x0,向左回溯,找到x=x-jx-j+1…x-1x0,其中0≤J≤N,使得条件概率为
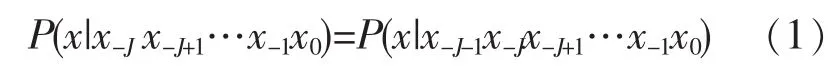
成立,设x=x-jx-j+1…x-1x0为x1的上下文环境. x1的上下文环境说明了影响符号x1的出现的历史追溯到x-J即可,不必再回溯到x-J-1以及更早的符号.要验证式(1)中的n个等式,需要根据序列x统计出字符串x-j-1x-j…x-1x0x和x-jx-j+1…x-1x0x出现的频数.统计频数的工作由如下的上下文树算法完成.
算法1:上下文树构造算法:
(1)初始化根节点,符号计数设置为0.
(2)假设根据字符串xt=x1x2…xt构造出树Tt,当前输入符号为xt+1,从根节点出发,按照字符串xtxt-1…的指引,访问Tt的结点,直到xt的符号用完,或者到了叶子结点.对每个访问到的结点,将该结点处的符号xt+1的计数增加1.
(3)如果最后一次访问到的结点xt+1处的计数≥2,创建一个新结点xt…xt-j+1xt-j,新结点xt+1处的计数置为1,其他符号的计数置为0,得到树Tt+1.
从上下文树构造算法可知,树Tt是一棵n元树,其高度随着从左到右扫描序列的时刻t增加而增加.n元树结点个数有如下性质:

命题2:高度为h的n元满树的长度为l(l≤h)的字符串个数为nl个.
2 基于压缩编码的上下文树算法
由于随机序列中符号出现的概率是非均匀分布的,利用熵压缩编码的原理可以对符号进行二进制变长压缩编码,二进制符号作为码元符号,随机序列中的自然语言符号可编码为变长的二进制串.本文在构建上下文树的时候,树的结点不是自然语言符号,而是仅含0,1的二元树,每个自然语言符号都对应着二元树上的一段路径.
算法2:基于压缩编码的上下文树算法.
(1)统计随机序列的符号的频率,构造Huffman编码,形成码表,用B(xi)表示自然语言符号x对应的二进制串.
(2)初始化根结点,符号计数置为0,令t时刻自然语言符号序列为xt=x1x2…xt.
(3)假设根据字符串xt=x1x2…xt构造出树Tt,当前输入为xt+1,从根结点出发,按照字符xtxt-1…的指引,访问Tt的结点,直到xt的符号用完,或者到了叶子结点,比如B(xt)…B(xt-j+1).对每个访问到的结点,将该结点处符号xt+1的计数增加1.
(4)如果最后一次访问到的结点xt+1处的计数≥2,创建一个新结点B(xt)…B(xt-j+1)B(xt-j),新结点处xt+1的计数置为1,其他符号的计数置为0,得到树Tt+1.
基于压缩编码的上下文树算法与上下文树算法不同点在于,将n元树化为二元树,n元树中的每个结点在二元树中扩展为一条路径.该路径对应着自然语言符号的Huffman编码.下面的结论表明,将n元树化为二元树,在表达相同数量的自然语言字符串情况下占用的内存却大大减少了.
命题3:设n元树的每个节点指针域占用字节数为d,数据域占用字节数为m,对n个符号采用二进制编码,平均码长为l0.则高度为h的n元满树所占用字节总数


表1 3个长度为62的字符串1-62阶条件概率计算结果范例Table 1 Computational results of 3 stings'conditional probability
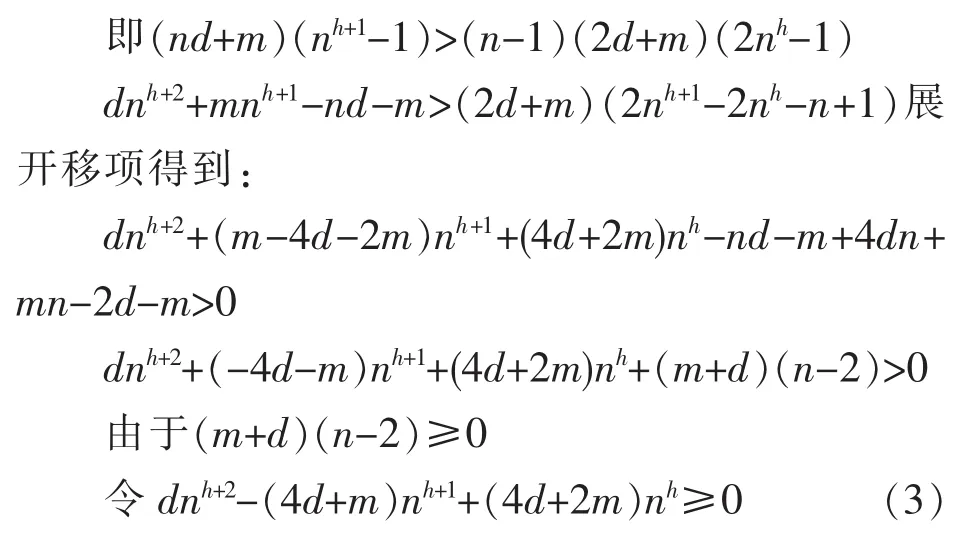
除以nh得到:

故关于n的不等式(4)有解
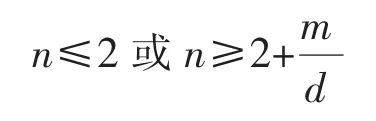
也即n≥2时结论成立.
3 实验结果
利用基于压缩编码的上下文树构造算法对英文长篇小说《Forrest Gramp》(Winston Groom,1986)开展了统计工作,程序运行环境为32位微软XP service pack3操作系统,Pentium Dual-Core E6700 CPU,主频3.20 GHz,内存2 GByte分析字符串长度达到62个自然语言符号时,运行时间约34分钟,统计出共281 705条长度为62的字符串,每个字符串分别计算出从1阶到62阶条件概率以供后续分析使用.表1给出了其中的3个计算结果.
从数据统计分析可以看出,符号的一阶统计特性可以在数值实验中得到,对文本信息的符号做二进制的压缩编码,在结构处理上采用二元树代替(>2)元树,在相同内存的存储空间下,理论上证明可以增加树的高度,实验也进一步验证结论.基于此,可以对长度更大的子串进行相关性检测,并且提高分析的精度.
[1]洪汉玉,章秀华,程莉.道路病害形态特征的图像分析[J].武汉工程大学学报,2014,36(4):70-76.
HONG Han-yu,ZHANG Xiu-hua,CHENG Li.Image analysis method for road disease morphology characteristic[J].Journal of Wuhan Institute of Technology,2014,36(4):70-76.(in Chinese)
[2]孙玉昕,章瑾.利用堆排序优化路径搜索效率的分析[J].武汉工程大学学报,2013,35(10):50-55.
SUN Yu-xin,ZHANG Jin.Practical analysis of improving path searching efficiency by heap sort[J].Journal of Wuhan Institute of Technology,2013,35(10):50-55.(in Chinese)
[3]王学华,刘莉君,马凡杰,等.数控激光加工路径链表快速搜索优化[J].武汉工程大学学报,2014,36(10):52-57.
WANG Xue-hua,LIU Li-jun,MA Fan-jie et al.Rapid routine searching of numerical control laser processing based on linked list structure[J].Journal of Wuhan Institute of Technology,2014,36(10):52-57.(in Chinese)
[4]徐超,周一民,沈磊.一种面向隐含主题的上下文树核[J].电子与信息学报,2010,32(11):2695-2700.
XU Chao,ZHOU Yi-min,SHEN Lei.A context tree kernel based on latent semantictopic[J].Journal of Electronics&Information Technology,2010,32(11):2695-2606.(in Chinese)
[5]RISSANEN J.A universal data compression system[J]. IEEE Transactions on information theory,1983,29(5):656-664.
[6]陈亮,孟庆愿,董彦磊,等.CTW无损压缩算法在管道无损检测中的应用[J].实验技术与管理,2012,29(6):42-47.
CHEN Liang,MENG Qingyuan,DONG Yanlei,et al. Using CTW lossless compression algorithm in pipelines nondestructive testing[J].Experimental Technology and Management,2012,29(6):42-47.(in Chinese)
[7]DUMONT Thierry.Context tree estimation in variable length hidden[J].IEEE Transactions on information theory,2014,60(6):3196-3208.
[8]GWADERA R,GIONIS A,MANNILA H.Optimal segmentation using tree models[J].Knowledge and Information Systems,2008,15(3):259-283.
[9]Martins D A,Neves A J R,Pinho A J.Variable Order Finite-Context Models in DNA Sequence Coding[C]// PatternRecognitionandImageAnalysis.Springer Berlin Heidelberg,2009:457-464.
[10]BÜHLMANN P.Model selection for variable length Markov chains and tuning the context algorithm[J]. Annals of the Institute of Statistical Mathematics,2000,52(2):287-315.
[11]CÉNAC P,CHAUVIN B,PACCAUT F,et al.Context trees,variable length Markov chains and dynamical sources[C]//Séminaire de Probabilités XLIV. Springer Berlin Heidelberg,2012:1-39.
Context tree algorithm based on compression encoding
FU Min1,2,DAI Zu-xu1,WANG Dao-peng2
1.College of Science,Wuhan Institute of Technology,Wuhan 430502,China; 2.Institute of Pattern Recognition and Artificial Intelligence,Multi-spectral Image Information Processing Key Laboratory of National Defense,Huazhong University of Science and Technology,Wuhan 430074,China
The context tree as a commonly used data structure plays a very important role in analyzing statistical characteristics of random sequence,and the random sequence of symbols generally comes from a fixed symbol set.The general context tree is a n-tree,in which n is more than 1.Because the tree is a kind of computer memory wasting data structure,a context tree construction algorithm based on compress coding was presented utilizing the first-order statistical properties of binary symbols.In the numerical experiment under the same memory storage space condition,the tree’s height has been greatly increased,and the accuracy of data analysis also improved.
context tree;n_gram tree;compression encoding
TP309.7
A
10.3969/j.issn.1674-2869.2015.04.012
1674-2869(2015)04-0056-03
本文编辑:陈小平
2015-01-12
湖北省自然科学基金重点项目(2010CDA009);湖北省自然科学基金一般项目(2009CDB367);国家自然科学基金面上项目(61175013);武汉工程大学校级教研项目(X2013021).
付敏(1979-),女,湖北襄阳人,讲师,博士研究生.研究方向:信息处理,计算机视觉.
