双目视图运动图像去模糊方法

洪汉玉，张文莫，章秀华,时愈

武汉工程大学机电工程学院，湖北 武汉 430205

双目视图运动图像去模糊方法

洪汉玉，张文莫，章秀华,时愈

武汉工程大学机电工程学院，湖北 武汉 430205

现代工业生产线上采集到的产品图像存在运动模糊，对后期探测产品表面信息以及重建产品轮廓产生影响.为了解决这一问题，提出一种基于双目视图的运动图像去模糊方法.通过双目相机之间的对极几何关系以及相机模型，推导出两视点图像点扩散函数路径之间的内在联系，并运用像机标定模块求取标定矩阵中的参数.通过此内在约束条件求取精确的点扩散函数，并对双目视点图像进行统一去模糊.结果表明，通过双视点图像几何关系求取的点扩散函数路径来进行去模糊取得了较好的效果.

运动去模糊；双目视图；张正友标定；对极几何；点扩散函数路径

0 引言

随着当代工业制造加工工艺的不断提升，产品加工过程也越来越强调技术的智能化，自动化［1］．生产上需要精确，自动以及高效的测量被测零件的外观轮廓，几何尺寸.而现代工业生产上零件外型复杂，测量又需要现场实时进行，传统的检测方法已经无法达到现代工业生产的需求［2］.

双目测量技术是计算机视觉的关键技术之一，通过从图像中提取有用的信息，处理被测图像以获得所需要的参数数据，然后通过双目相机之间的几何限定条件来求得物体运动轨迹在双目相机上的投影关系，进而建立双目视点图像模糊核路径关系并对其进行整体一致性的精确优化［3］.这种非接触测量具有效率高，系统结构简单，精确度高，自动化程度高，成本低廉等优点［4］，非常适合于制造现场的在线，非接触产品测量检测和质量控制［5］.由于双目测量系统能够很大程度的满足现代先进制造业的要求，所以其在医学、交通、工业、航空航天领域都有广阔的发展前景.

1 相机模型与图像标定

1.1 摄像机模型参数

相机标定主要包含以下参数.

相机内部参数：

其中，u0、v0为光学中心的坐标，fx、fy分别是u轴和v轴上的有效焦距，s是u轴和v轴上的不垂直因子［6－7］，在理想情况下令s＝0.

相机外部参数：

式（2）中，R为相机旋转矩阵而T为相机平移向量，通常将R和T称为外部参数［8］.

而对于非线性模型的内部参数还包括两个径向畸变参数k1，k1以及两个切向畸变参数p1，p2［9-10］.

1.2 坐标系转换与相机模型

对于双目相机的标定系统总共包含四个不同的转换坐标系，它们分别是：摄像机坐标系：ocxcyczc；世界坐标系：owxwywxw；图像（CCD）坐标系：oxy和计算机图像坐标系：uv［11］；各个坐标系之间存在相互转换关系如下.

根据小孔成像模型，可以得到从摄像机坐标系到图像坐标系有如下变换关系：

从图像坐标系到计算机坐标系得变换：

式（4）中dx是每个像素在x方向上的物理长度，dy是每个像素在y方向上的物理长度，（cx，cy）为图像中心坐标.

从而可以知道世界坐标系到摄像机坐标系之间的变换如下：

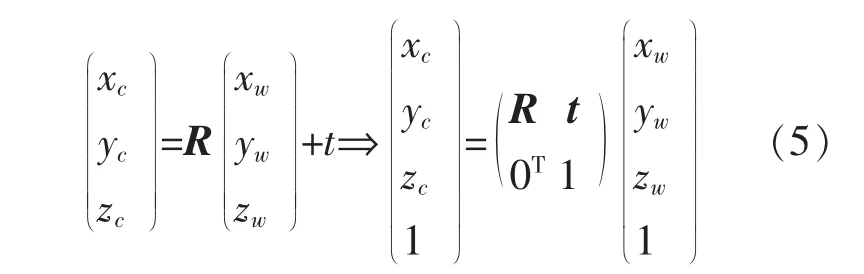
可以得到世界坐标系表示的P点坐标与其投影点p的计算机图像坐标（u，v）的变换关系：

根据针孔相机成像原理，由世界坐标点到理想像素点变换如下：

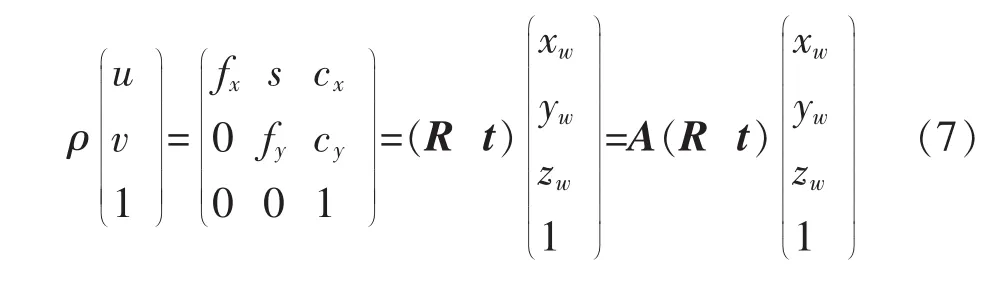
2 双目相机PSF之间的几何关系推导

2.1 双目相机极线约束方程

对极几何是指双目视图两视点之间的内在影射几何，它与外部的景物结构无关，只决定于双目摄像机的相对距离和内部参数［12－14］.立体匹配中双目相机之间存在如下几何关系（见图1）．

其中，P点为空间任一点P在图像I1上的投影，P2点为空间任一点P在图像I2上的投影，直线l1为成像面I1上对应于P2点的极线，同样直线l2为成像面I2上对应于P1点的极线.如果已知P1点在图像I1上的位置，则在图像I2内P1点所对应的点必然位于它在图像I2的极线上，即P2点一定在直线l2上.这就称为极线约束［15］.

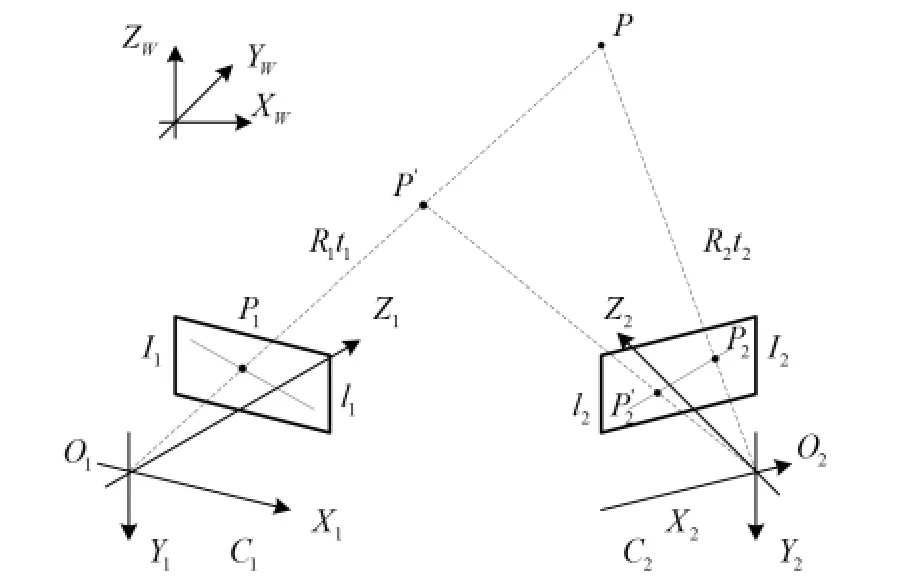
图1 双目相机对极几何关系Fig.1 The epipolar geometry relationship between binocular cameras

由于双目相机分别为小孔成像模型，可以将两个相机的投影方程联立：

此方程称为极线约束方程，其中，Xw为空间某点P处于世界坐标系之下的齐次坐标；pl和pr是P点分别投影在左右视点图像的齐次坐标.将标定矩阵拆分，将Ml与Mr矩阵中左边的3×3部分别写成Ml1和Mr1，右边的3×1部分则分别写作ml和mr.

如果将Xw记作Xw＝（X 1）T，其中X＝（Xw，Yw，Zw）T.于是可将式（8）写作：

联立此方程，消去X可得

由于等式两边都是三维向量，式（10）中其实为三维方程，将此等式两边消去sl与sr可以得到一个关于pl和pr的关系式.通过一系列变换，可以得到pl和pr之间的关系为

2.2 双目动目标模糊路径分析

因为对于运动模糊，模糊路径即为物点在三维空间运动轨迹在成像面上的投影.因此，只需分别计算出物体上一点P在左视点上模糊路径的起止点坐标pl1，pl2，便可以通过式（11）计算出其在右视点上对应的模糊路径起止点坐标pr1，pr2，如图2所示，线段pl1pl2，pr1pr2分别为左右视点平面上的理想点扩散函数路径.

图2 双目视图运动轨迹投影Fig.2 The motion trajectory projection of binocular cameras

对于单视点模糊图像，各视点图像可由式（13）描述：

其中gi（x，y）为实际观测图像即模糊图像，hi（x，y）为图像点扩散函数PSF，fi（x，y）为原清晰图像，ni（x，y）为图像中包含的噪声，⊗表示二维离散去卷积［16］.对于理想运动模糊而言，模糊核为具有一定方向的单像素直线段或光滑曲线段.

2.3 基于边缘检测的单视点图像运动模糊核估计

图像复原的质量体现在对模糊核的精确估计之上，模糊图像的模糊边缘可以看做是一个理想的逐像素阶梯状边缘被一个模糊算子卷积而成［17］.对于模糊图像，图像清晰边缘的位置可以看做是未改变的，只有清晰边缘两侧区域的像素灰度值发生了改变.可以利用高斯差分算子（DoG算子）分别与清晰边缘与模糊边缘做卷积，通过估计模糊边缘并以此为基础预测边缘两边的清晰区域［18］.

3 实验设计与结果分析

3.1 实验设计

（1）图像采集.实验平台由实验台，光源及幕布，小车，棋盘格标定板，双目相机及工控机组成.采集图像步骤如下：首先固定双目相机，设置相机参数及焦距，对双目相机进行标定，然后让被测物体匀速直线运动通过视平面，采集运动模糊图像.模糊长度由相机曝光时间控制.本实验双目相机采用微视MV－3000UC相机.

（2）图像的预处理.因为采集到的图像中包含了噪音以及许多与目标无关的图像信号，因而需要对原始图像采取一定的预处理.图像的预处理是为了将图像无关的背景进行抑制，从而提高信噪比.

（3）相机标定.因为双目图像点扩散函数路径之间存在关系仅仅由相机的几何位置关系及相机成像模型决定，因此在求取点扩散函数路径关系式时所包含的未知参数即为相机的内参和外参.相机的内外参数由相机标定矩阵给定，而相机的标定矩阵可以用张正友棋盘格标定法求取，具体步骤如下：

张正友标定算法基本原理式：

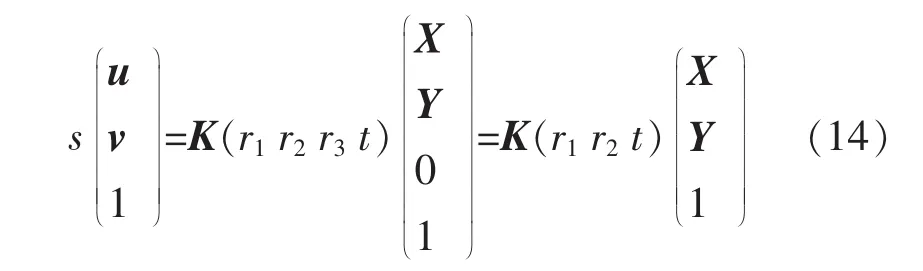
其中（X Y 1）T为模板上点的齐次坐标，（u v 1）T为模板上对应点投影到图像平面上的坐标.首先准备一幅棋盘标定板，在固定双目相机并设定参数之后，分别用双目相机拍摄标定板，通过Harris算子提取角点，计算出相机的内外参数.

（4）模糊图像点扩散函数路径的计算.将标定矩阵进行拆分，带入式（10）求取左右视点图像上对应点之间的数量关系，通过一个视点的点扩散函数路径求取另一个视点的扩散函数.

（5）通过计算所得的点扩散函数路径对实验图像进行去模糊.

3.2 实验结果与分析

本文所采用算法通过计算机编程实现.

图3为用单帧去模糊方法分别对左右相机视点进行单帧去模糊的结果.由图3可见，单帧去模糊方法所估算的点扩展函数路径（PSF）为一团离散的点阵.去模糊效果也不太理想，尤其是图像边缘，存在较为明显的重影，这是由于粗略估算的PSF路径上存在许多不真实的点，与原始模糊图像进行迭代去卷积的过程中，使图像边缘产生了振铃效应.图4为精确优化后的PSF复原结果.因为优化过程中考虑到了双目视点之间的几何对应关系，因此更接近于实际PSF值，使得图像边缘更为清晰，辨识度更高.表1为两种方法复原图像的归一化的均方差值对比，表2为两种复原方法的峰值信噪比对比.两种评价指标都反映出，用精确优化的PSF进行图像复原效果更好.

由实验可见，通过双目相机间的几何约束关系求取的模糊核去模糊效果较好.因为此方法中某一视点的模糊核由另一视点上起止点的坐标以及相机参数通过矩阵运算求得，而实际检测中，相机参数是连续的，通常精确到小数点后三位，而PSF是以像素为单位离散的.若模糊长度较小，在后续近似计算中会产生很大误差，这部分误差可以通过增大采集图像分辨率来减小.而图像PSF计算的精确性由相机矩阵的标定来决定.

图3 用单帧去模糊方法估计PSF去模糊结果Fig.3 The deblurring result with the PSF based on traditional deblurring method

图4 用约束条件求取的PSF去模糊Fig.4 The deblurring result with our method

表1 去模糊质量NMSE值对比Table 1 Comparison of NMSE values

表2 去模糊质量PSNR值对比Table 2 Comparison of PSNR values

4 结语

由于实际生产线上的工件往往处于运动状态，取得的图像会产生运动模糊.而以往的图像复原算法又通常只着眼于对单视点图像进行单独的模糊核估计及图像复原，不能很好的保持各个视点之间点扩展函数路径的几何对应关系.以上叙述的方法正是针对此类问题提出.该方法推导了双目相机之间的对极几何关系并结合现有的非盲目去卷积算法，对双目运动模糊图像进行整体一致的去模糊处理，并进行了一系列复原实验.实验结果表明本文提出的复原方法是有效的.

致谢

衷心感谢国家自然科学基金委员会的资助！

［1］洪汉玉．现代图像图形处理与分析［M］．武汉：中国地质大学出版社，2011：1－2．

HONG Han－yu．Advanced processing and analysis for image and graphics［M］．Wuhan：China University of Geosciences press，2005：11－12．（in Chinese）

［2］张天序．成像自动目标识别［M］．武汉：湖北科学技术出版社，2005：11－12．

ZHANG Tian-xu．The automatically recognizes of imaging［M］．Wuhan：Hubei Science and Technology Press，2005：11－12．（in Chinese）

［3］卢在盛．单幅图像运动模糊参数判定与去模糊研究［D］．广西：广西大学，2011．

LU Zai-sheng．Motion-blur indentification and delurring usingsingleimage［D］．Guangxi：Guangxi University，2011．（in Chinese）

［4］沈垣，李舜酩，毛建国，等．数字图像复原技术综述［J］．中国图像图形学报，2009，14（9）：1764－1775．

SHEN Yuan，LI Xunmin，MAO Jianguo，et al．Digital image restoration techniques［J］．Journal of Image and Graphics，2009，14（9）：1764－1775．（in Chinese）

［5］焦继超，赵保军，陶芬芳，等．一种基于局部图像复原的天文图像增强算法［J］．仪器仪表学报，2011，32（7）：1455－1461．

JIAO Ji-chao，ZHAO Bao-jun，TAO Fen-fang，et al．Astronomical image enhancement algorithm based on regional image restoration［J］．Chinese Journal of ScientificInstrument，2011，32（7）：1455－1461．（in Chinese）

［6］张红民，陈新平，张亚娟．一种改进的Wiener滤波图像复原算法［J］．重庆理工大学学报自然科学，2010，24（7）：76－80．

ZHANG Hong-min，CHEN Xin-ping，ZHANG Ya-juan．Improved wiener filter algorithm for image restoration［J］．Journal of Chongqing Insitute of Technology Natural Science，2010，24（7）：76－80．（in Chinese）

［7］RASKAR R，AGRAWAL A，TUMBLIN J．Coded exposure photography：Motion deblurring using fluttered shutter［J］．ACM Trans Graph，25（3）：795－804．

［8］SIMON M K Probability distributions involving gaussian randomvariables：ahandbookforengineers［J］. Scientists and Mathematicians Springer,2002：1378-1382．

［9］HONG Han-yu，ZHANG Tian-xu．Fast restoration approach for rotational motion blurred image based on deconvolutionalongtheblurringpath［J］．Optical Engineering，42（12）:3471－3486．

［10］LEVIN A.Blind motion deblurring using image statistics［C］//In Advances in Neural Information Processing Systems NIPS．2006（2）：1738－1742．

［11］CHEN W G，NANDHAKUMAR N，MATIN W N．Image motionestimationfrommotionsmear－anew computational model［J］．Pattern Analysis and Machine Intelligence，1996，18（4）:412－425．

［12］RAV－AchaA，PELEGS．Two motion－blurred images are better than one［J］．Pattern Recognition Letters，2005,26（2－3）：311－317．

［13］BEN ME，Nayar S K．Motion－based motion eblurring［J］．IEEE Trans on Pattern Analysis and Machine Intelligence，2004，26（6）：689－698．

［14］YUAN L，SUN J，QUAN L，et al．Shum Image deblurring with blurred／noisy image pairs［J］.ACM TOG，26（3），374－379．

［15］YITZHAKY Y I，MOR A L，KOPEIKA N．Direct method for restoration of motion blurred images［J］. J Opt Soc Am A,15（6）:1512－1519.

［16］TSIN Y，RAMESH V，KANADE T.Statistical calibration of CCD image process［J］．Proc IEEE Int’l Conf Computer Vision，2001：480－487．

［17］HAMMETT S T，GEORGESON M A，GOREA A. Motion Blur and Motion Sharpening：Temporal Smear and Local Contrast Non-linearity［J］．Vision Resarch，1988（38）:20－99．

［18］章秀华，洪汉玉，华夏，等．动目标多视点基于标定的去模糊方法［J］．武汉工程大学学报，2014，36（12）：56－62．

ZHANG Xiuhua，HONG Han-yu，HUA Xia，et al．Multi－view motion of moving target deblurring based on calibration［J］．JournalofWuhanInstitute ofTechnology，2014，36（12）：56－62．（in Chinese）

Deblurring of double view motion image

HONG han－yu，ZHANG Wen－mo，ZHANG Xiu－hua，SHI Yu
School of Mechanical and Electrical Engineering，Wuhan Institute of Technology，Wuhan 430205，China

The images acquired from the actual production line in modern industrial production are motionblurred，which affects the detection of the surface information and the reconstruction of the profile．To solve this problem，we proposed a deblurring method based on double view motion image．We deduced the relationship of the point spread function path between the double view images through the epipolar geometry and the camera model，and solved the parameters in the calibration matrix with the calibration system based on MATLAB，then we got the association point spread function（PSF）path based on the constraint condition，and deblurred the motion images．The experimental results show that the motion image deblurring using the PSF path solved by the geometric relationship has better effect．

motion deblurring；binocular image；Zhengyou Zhang calibration；the epipolar geometry；point spread function path

TB35

A

10.3969/j.issn.1674-2869.2015.04.010

1674-2869（2015）04-0045-06

本文编辑：陈小平

2015-03-05

国家自然科学基金面上项目(61175013)；湖北省自然科学基金创新群体项目（2012FFA046）；武汉市国际科技合作计划项目（编号2014030709020310）.

洪汉玉(1964-)，男，湖北阳新人，教授,博士．研究方向：图像处理与模式识别.