三轴数控机床几何误差测量与辨识的研究

邹华兵

(广东工业大学广东省微纳加工技术与装备重点实验室，广东 广州 510006)

如何进一步提高数控机床的加工精度是先进制造技术的重要研究课题。几何误差补偿技术是提高数控机床加工精度的有效方法之一，而几何误差的精确辨识是实现误差补偿的前提［1-2］。三轴数控机床在其加工过程中有21 项几何误差，即机床沿着每个轴运动时的3 个转角误差和3 个线性位移误差，以及3 个轴间的垂直度误差［3-5］。数控机床几何误差的辨识过程是一项复杂且费时的工作，国内外许多科研学者开展了大量的相关研究，开发出了不少的误差辨识法，常见的有22 线法、15 线法、14 线法、9 线法等［6］。这些辨识法各具特色，为几何误差的辨识提供了许多的选择，但它们的测量线路都比较复杂，测量周期太长。虽然9线法的检测线数相对较少，但其求解过程需要6 个方程间的相互叠代，这必然会累加其中的测量误差［7］。测量点坐标的测量不可避免地也会产生测量误差从而影响几何误差的辨识精度。因此，为了提高几何误差的求解精度和效率，在其辨识过程中应尽量减少参与辨识的未知数和激光测量线数。

1 六线辨识法的推导

为了便于表述，本文主要以机床沿X 轴运动为例进行研究，沿Y 轴和Z 轴运动时的分析方法与其相同。机床工作台上一给定点(x，y，z)沿X 轴运动时，在X、Y、Z 方向上分别有线位移误差δx(X)、δy(X)、δz(X);绕X、Y、Z 方向分别有转角误差εx(X)、εy(X)、εz(X)，其中εx(X)为滚转误差，εy(X)为偏摆误差、εz(X)为俯仰误差［8-11］。用激光干涉仪可分别测量出在X 方向的定位误差Δx(X)，在Y 方向的直线度误差Δy(X)和在Z 方向的直线度误差Δz(X)。根据几何误差的基本特征，可以得到方程组(1)［12-14］。

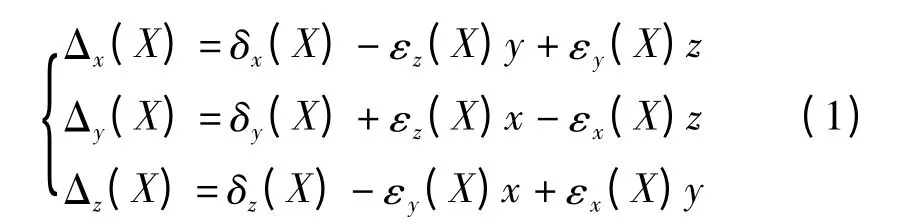
激光干涉仪，不仅能测量直线度误差，还能测量偏摆误差εy(X)和俯仰误差εz(X)。转角误差会使得不同测量点测得的机床运动到同一位置处的直线度误差不同。如图1 所示，由于偏摆误差εy(X)，在A 和B 两点分别测得机床运动到C 点处的直线度误差Δy(X)不同。但机床运动部件属于刚体，同一时刻运动部件上每一点处的偏摆误差和俯仰误差应是相同的。因此，使用激光干涉仪测量机床运动部件的直线度误差时需要准确测量出测量点的坐标，而测量其转角误差时就不需要［14］。

在机床坐标系中，选择两条直线1、2，分别在其上再选取点D1和D2作为测量点，如图2 所示。在工作台坐标系中，分别测量出D1和D2两点的坐标并记为D1(x1，y1，z1)和D2(x2，y2，z2)。让工作台沿X 轴运动，在点D1(x1，y1，z1)或D2(x2，y2，z2)的测量线上测量出偏摆误差εy(X)和俯仰误差εz(X)。在点D1(x1，y1，z1)处测量出直线1 的定位误差Δx1(X)及直线度误差Δy1(X)、Δz1(X);在D2(x2，y2，z2)点测量出直线2的直线度误差Δy2(X)。那么根据公式(1)可代换出方程组(2):

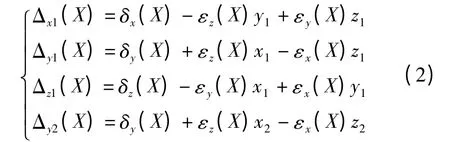
解方程组(2)得:

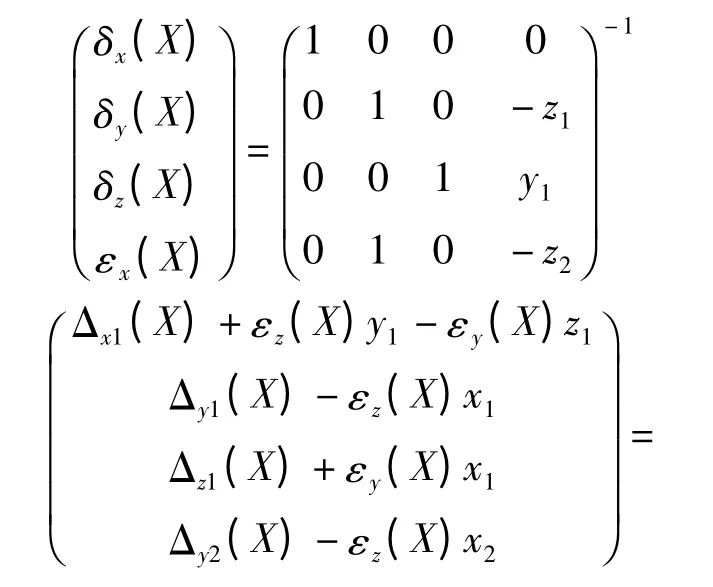
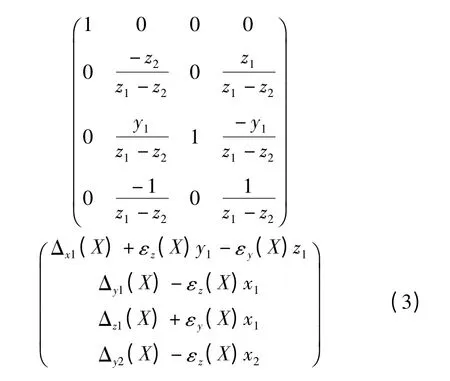
从方程组(3)可知，只要选取的点D1(x1，y1，z1)与D2(x2，y2，z2)中的z1与z2不相等，方程组(3)就有唯一解，即能够辨识出机床沿X 单轴运动时产生的6项几何误差。

六线法对轴间垂直度误差的辨识原理与九线法的相同。以X 轴与Y 轴间的垂直度误差为例。沿直线1测量出机床沿X 轴运动在Y 方向的直线度误差Δy(X);沿直线3 测量出机床沿Y 轴运动在X 方向的直线度误差Δx(Y)。运用最小二乘法将Δy(X)和Δx(Y)拟合成如图3［15］所示的两条虚线。

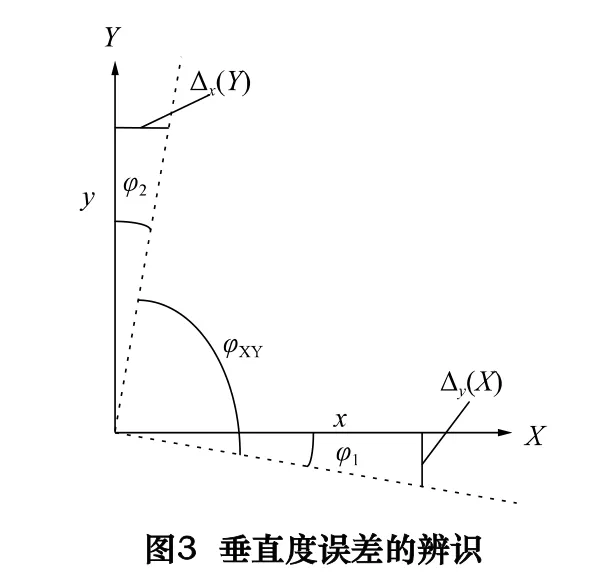
那么各角与坐标间的关系为:

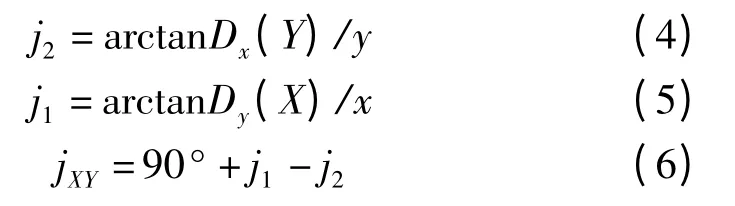
因此，X 轴与Y 轴间的垂直度误差为:

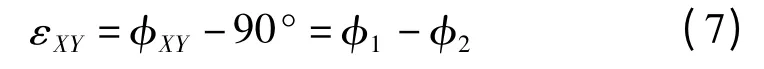
如果εXY＞0，表示X 与Y 轴间的夹角大于90°，可用正数表示，反之就取为负数。

用同样的原理可以求出X 轴与Z 轴间的垂直度误差εXZ和Y 轴与Z 轴间的垂直度误差εYZ［16］。因此，采用六线几何误差辨识法可以较快地辨识出三轴数控机床的21 项几何误差参数。

2 实验研究

由于六线法与九线法对轴间垂直度误差的辨识方法相同，其辨识原理已被广泛认可。因此，本文只需对六线法辨识的机床沿单轴运动的6 项几何误差进行实验分析。

2.1 六线法的辨识

在工作台坐标系下，选择第一测量点D1(50，60，25)。在此点测得机床沿X 轴运动时的几何误差数据如表1 所示。

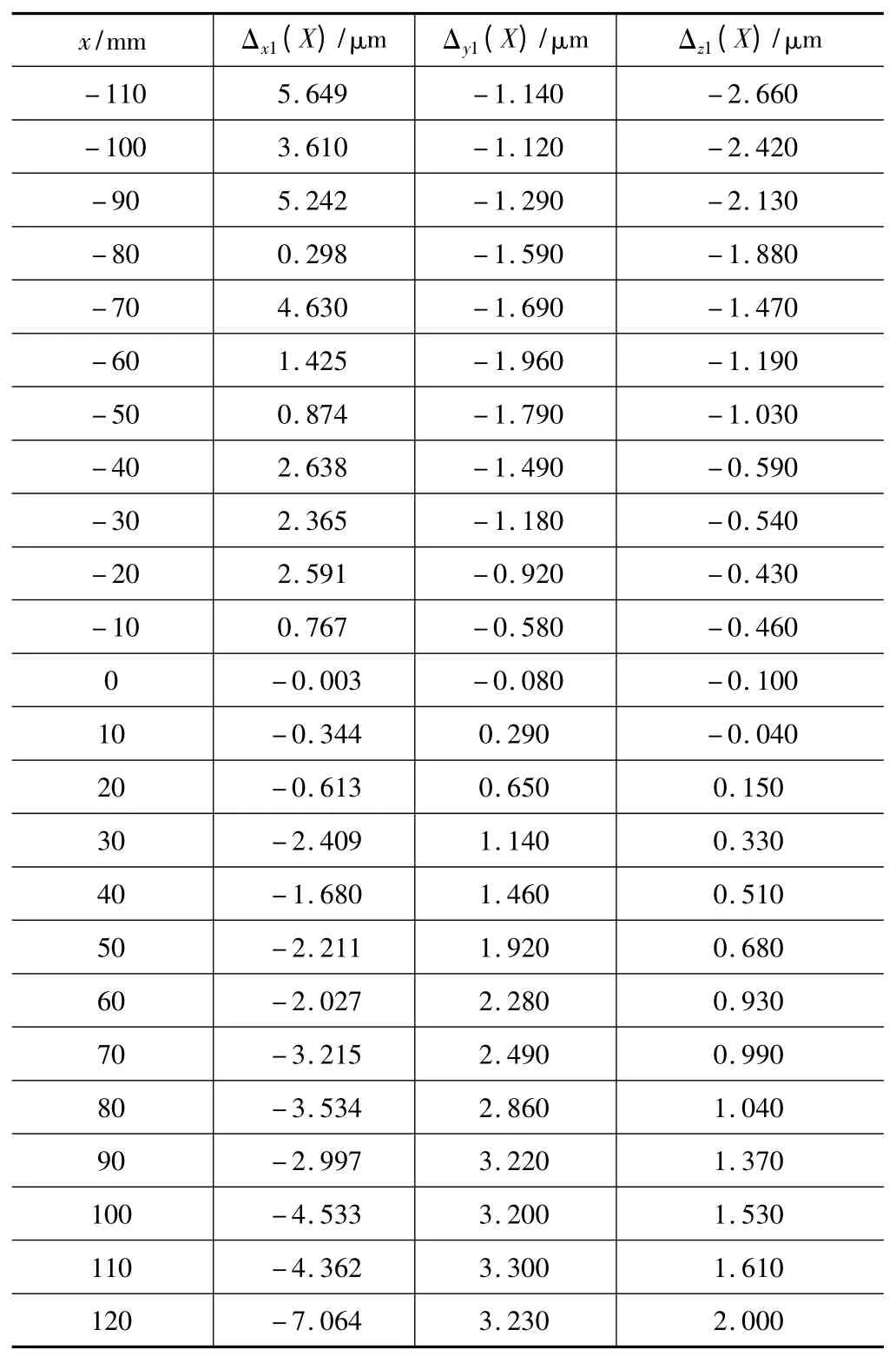
表1 第一线的测量数据

在工作台坐标系下，选择第二测量点D2(-90，60，75)。在此点测得机床沿X 轴运动时的几何误差数据如表2 所示。

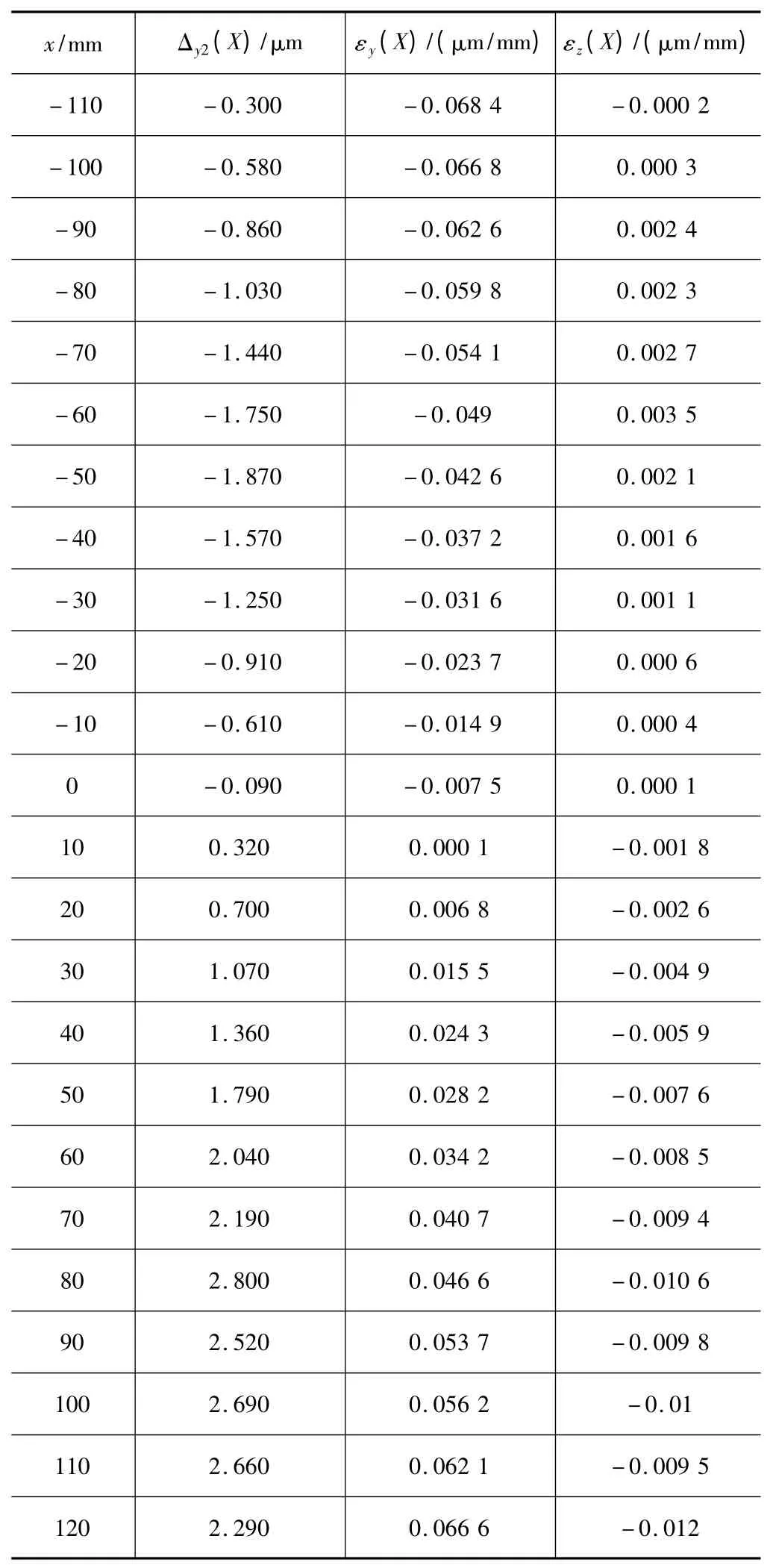
表2 第二线的测量数据

把点D1(50，60，25)和D2(-90，60，75)的坐标以及表1 和表2 中的数据分别代入公式(3)可得表3。

2.2 六线辨识法的验证

在工作台坐标系下，选择第三测量点E(-80，50，30)。在此点测得机床沿X 轴运动时在Y 方向上的直线度误差Δy(X)'，如表4 所示。

表3 六线法辨识的数据

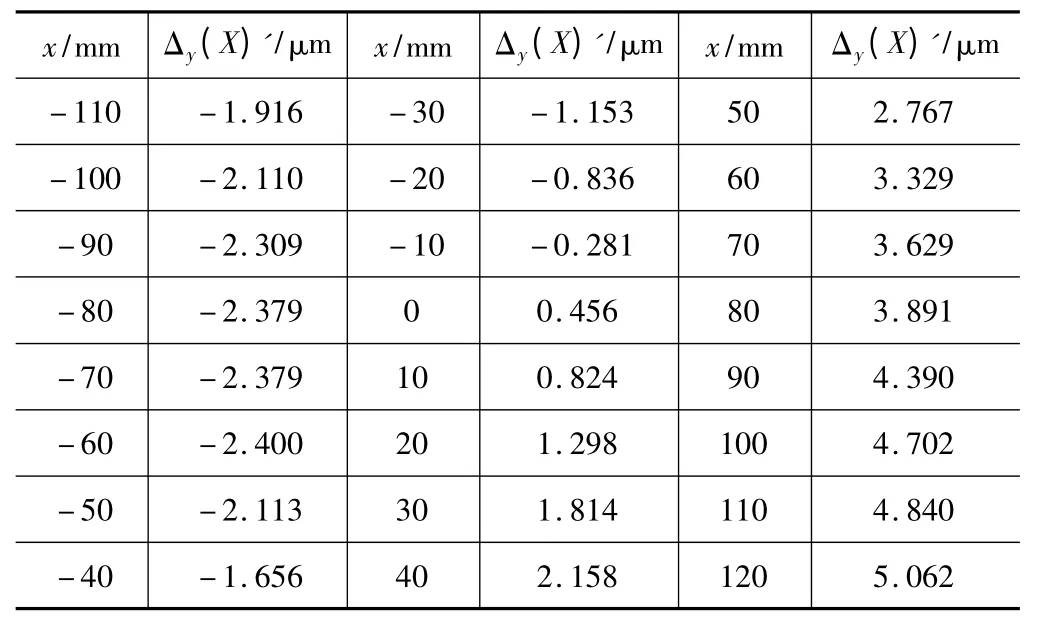
表4 E 点处的测量数据

将点E(-80，50，30)的坐标以及表3 的数据代入公式(1)可计算出机床沿X 轴运动时在Y 方向上的直线度误差Δy(X)，如表5 所示。

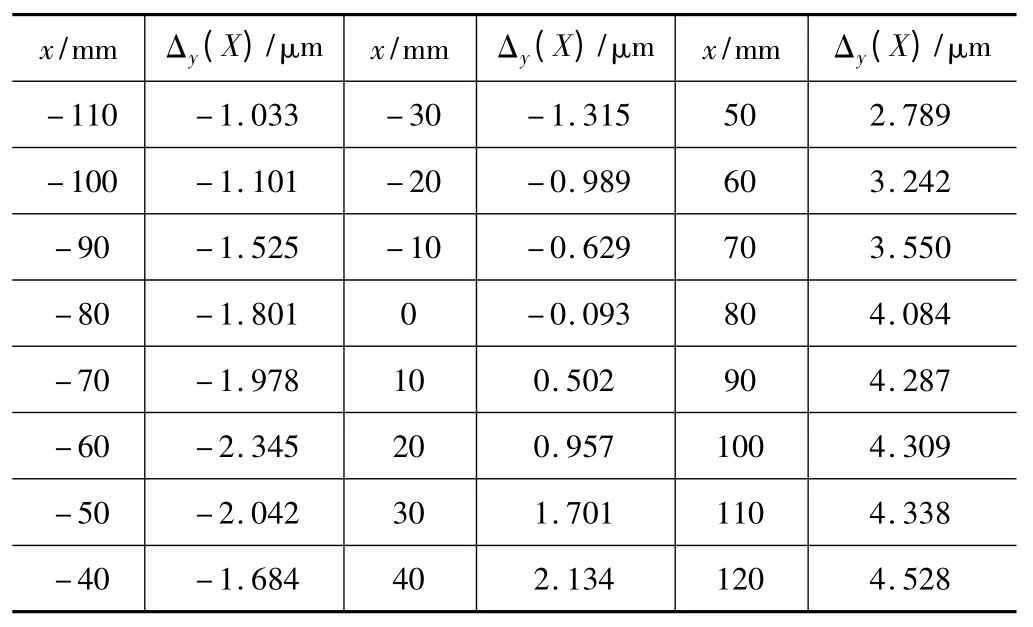
表5 E 点处的预测数据

将表4 中的测量数据Δy(X)'和表5 中的预测数据Δy(X)分别绘图可得图4。

从图4 可知，用六线几何误差辨识法计算出的直线度误差值与用激光干涉仪直接测量出的直线度误差值相近。这说明六线几何误差辨识法是科学的、可靠性。

3 结语

(1)本文介绍了转角误差会使得不同测量点测得的机床运动到同一位置处的直线度误差不同，而不同测量点测得的偏摆误差和俯仰误差应是相等的。

(2)根据几何误差的基本特征，本文探研出了一种仅需测量6 线就可以辨识出三轴数控机床21 项几何误差的新方法，用实验数据对探究出的六线几何误差辨识法进行了实例演算，并验证了六线几何误差辨识法是科学的、可靠的。

［1］Dong-Mok Lee，Zankun Zhu，Kwang-Il Lee，et al.Identification and measurement of geometric errors for a five-axis machine tool with a tilting head using a double ball-bar［J］.International Journal of Precision Engineering and Manufacturing.2011，12(2):337-343.

［2］Xiang Sitong，Yang Jianguo，Zhang Yi.Using a double ball bar to identify position-independent geometric errors on the rotary axes of five-axis machine tools［J］.The International Journal of Advanced Manufacturing Technology，2014，70(9-12):2071-2082.

［3］Zhu Shaowei，Ding Guofu，Qin Shengfeng，et al.Integrated geometric error modeling，identification and compensation of CNC machine tools［J］.International Journal of Machine Tools ＆ Manufacture 2012，52(1):24-29.

［4］Schwenke H，Knapp W，Haitjema H，et al.Geometric error measurement and compensation of machines—An update［J］.CIRP Annals-Manufacturing Technology，2008，57(2):660-675.

［5］Tian Wenjie，Gao Weiguo，Zhang Dawei，et al.A general approach for error modeling of machine tools［J］.International Journal of Machine Tools＆ Manufacture 2014，79:17-23.

［6］曲智勇，陈维山，姚郁.导轨几何误差辨识方法的研究［J］.机械工程学报，2006，42(4):201-205.

［7］郑剑.机床几何误差对在线测量精度的影响研究［D］.南京:南京航空航天大学，2008.

［8］Lei W T，Hsu Y Y.Accuracy test of five-axis CNC machine tool with 3D probe-ball.Part II:errors estimation［J］.International Journal of Machine Tools ＆ Manufacture 2002，42:1163-1170.

［9］Kong L B，Cheung C F，To S，et al.A kinematics and experimental analysis of form error compensation in ultra-precision machining［J］.International Journal of Machine Tools ＆ Manufacture，2008，48(12-13):1408-1419.

［10］Cui Gangwei，Lu Yong，Gao Dong，et al.A novel error compensationimplementing strategy and realizing on Siemens 840D CNC systems［J］.The International Journal of Advanced Manufacturing Technology，2013，61(5-8):595-608.

［11］Kong L B，Cheung C F.Prediction of surface generation in ultra-precision raster milling of optical freeform surfaces using an Integrated Kinematics Error Model［J］.Advances in Engineering Software，2012，45(1):124-136.

［12］刘又午，刘丽冰，赵小松，等.数控机床误差补偿技术研究［J］.中国机械工程，1998，9(12):48-52.

［13］郭前建.数控滚齿机几何误差与热误差实时补偿技术研究［D］.上海:上海交通大学，2008.

［14］李小力.数控机床综合几何误差的建模及补偿研究［D］.武汉:华中科技大学，2006.

［15］Lee Jae Ha，Liu Yu，Yang Seung-Han.Accuracy improvement of miniaturized machine tool:Geometric error modeling and compensation［J］.International Journal of Machine Tools ＆ Manufacture，2006，46(12/13):1508-1516.

［16］粟时平.多轴数控机床精度建模与误差补偿方法研究［D］.长沙:国防科技大学，2002.