An Approach to Underwater Image Enhancement Based on Image Structural Decomposition

JI Tingting, and WANG Guoyu

College of Information Science and Engineering,Ocean University of China,Qingdao266100,P. R. China

An Approach to Underwater Image Enhancement Based on Image Structural Decomposition

JI Tingting, and WANG Guoyu*

College of Information Science and Engineering,Ocean University of China,Qingdao266100,P. R. China

Underwater imaging posts a challenge due to the degradation by the absorption and scattering occurred during light propagation as well as poor lighting conditions in water medium. Although image filtering techniques are utilized to improve image quality effectively, problems of the distortion of image details and the bias of color correction still exist in output images due to the complexity of image texture distribution. This paper proposes a new underwater image enhancement method based on image structural decomposition. By introducing a curvature factor into the Mumford_Shah_G decomposition algorithm, image details and structure components are better preserved without the gradient effect. Thus, histogram equalization and Retinex algorithms are applied in the decomposed structure component for global image enhancement and non-uniform brightness correction for gray level and the color images, then the optical absorption spectrum in water medium is incorporate to improve the color correction. Finally, the enhanced structure and preserved detail component are recomposed to generate the output. Experiments with real underwater images verify the image improvement by the proposed method in image contrast, brightness and color fidelity.

underwater image; image structural decomposition; image enhancement; retinex

1 Introduction

Underwater imaging is a difficult task because of natural limitation of light transmission in water medium. Absorption and scattering effects degrade the quality of images inevitably during imaging process as the forward scattering causes images blurred and the backscattered light introduces the noisy background to images. Moreover, the degradation often comes from poor lighting conditions,i.e., the non-uniform brightness of a target within a small field of view illumination. Underwater image recovery has been widely investigated using various approaches that can be classified into two main categories： image restoration and image enhancement (Raimondo and Silvia, 2010). Image restoration methods try to recover the true image as a solution of optimal estimation via the prior knowledge of the image formation. But the common aporia in such solutions is just the lack of knowledge of imaging environment, particularly, the intrinsic optical properties (IOP) (Dubreuilet al., 2013) in real underwater image processing. In many applications, however, improvement of observations is commonly desired and can be facilitated with image enhancement techniques, without the prior knowledge of the IOP. Image enhancement employs various filtering techniques toimprove image quality. But due to the complexity of image texture distribution, problems, such as distortion of output image details and bias of color correction, are frequently encountered in applications. One of the expected solutions is to apply the image structural decomposition to image enhancement, where the global filter and correction are specifically applied to the corresponding structure component of the decomposed image while image information is preserved as much detailed as possible.

Generally, an image,f(x,y), can be decomposed into the structure component,u(x,y), and the detailed component,g(x,y), as follows：

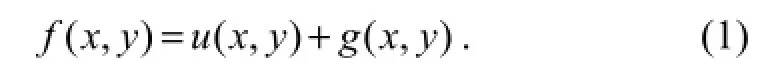
In underwater imaging processes, a small field of view illumination and light attenuation yields to the nonuniform brightness of the image and the bias of color distribution, which are merely globally represented in the structure component of the sensed image. Based on the MSG method a curvature-based decomposition model is proposed in this study. The model is referred to as the P_MSG method, in which the gradient effect in image decomposition is eliminated. Also the Retinex algorithm (Morelet al., 2010) is applied to structure components for global color and non-uniform brightness correction, and the optical absorption spectrum in water medium is incorporated to improve the color correction. The final enhanced image is generated by recomposing the correctedstructure and preserved detailed components.

2 P_MSG Decomposition Model

Since the Mumford-Shah functional decomposition model (MS model) was first proposed in 1985 (Mumford and Shah, 1988), it has been widely investigated as one of the PDE methods in the image analysis. To facilitate the representation of the image texture, Meyer (2001) defined a Banach space G based on total variation. It has been proved that the G space possesses high oscillation characteristics and is capable of describing image details. Consequently, the so-called MSG (Mumford_Shah_G, 2008) model was proposed by the combination of the MS model (Strekalovskiyet al., 2012) and the G space, which theoretically ensures adequate detailed components in image decomposition. The MSG model is formulated as the minimization of energy (Wanget al., 2008)：

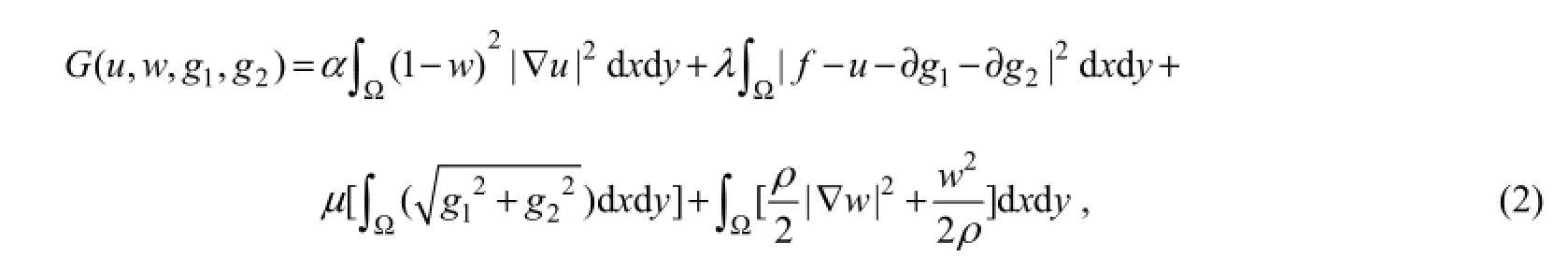
whereuis the structure component;g1andg2are the horizontal and vertical detailed components respectively;λ,αandμare the positive weights;wis the indicator of image edgels (w≅0 at a non-edgel point andw≅1 at an edgel point). The coefficientρis positive. The first term on the right hand side of Eq. (2) is the smoothness constraint of the structure component. The second term is the minimization of the decomposition error and is datadependent. The third term is the oscillation constraint of the texture component and is the minimization of the G space norm of the texture component. The last term is the simplification of edges aswis close to either 0 or 1.

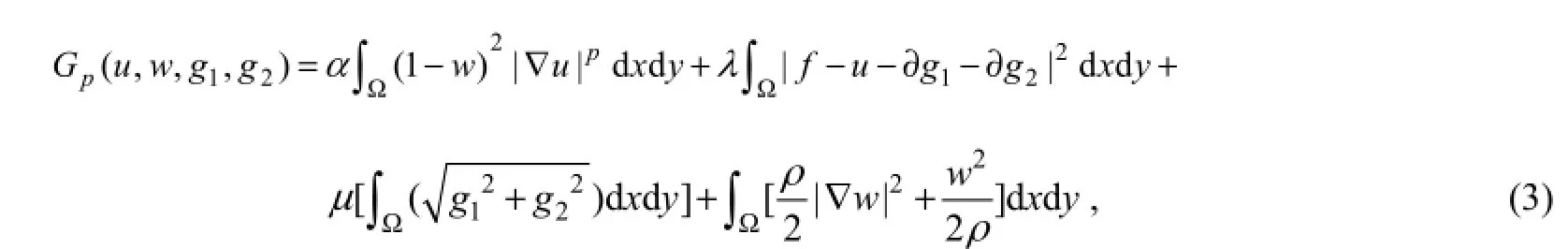
where

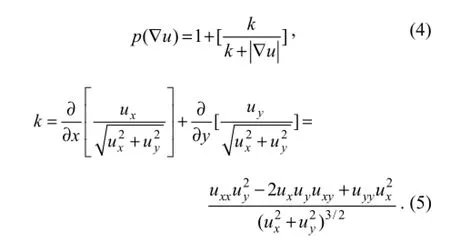
Therefore,

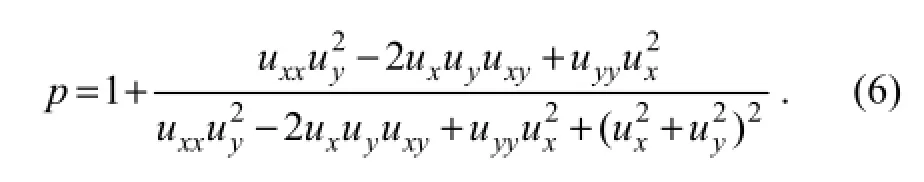
From Eq. (3) the Euler-Lagrange expression with respect tou,g1,g2, andwis

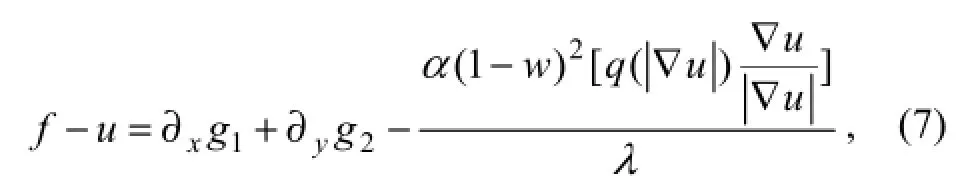
where

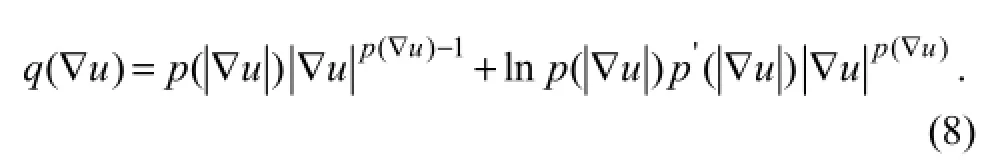
Letp(|∇|) be constant, and the following equations are obtained

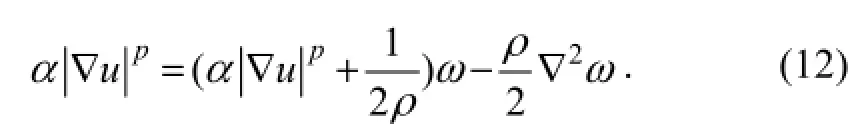
Assuming linear processing the solution of Eqs. (9)-(12) can be derived through iterative computation as

Afterniterations, the image details,, and the image structure,un+1(x,y), are obtained. Therefore,

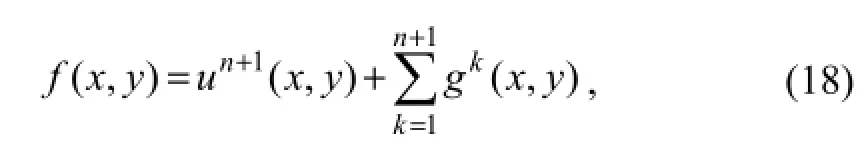
A comparison between the MSG method and the P_MSG method is shown in Fig.1. It can be seen from the squared areas that the proposed P_MSG method effectively improves the gradient effect while the fine details are still preserved.

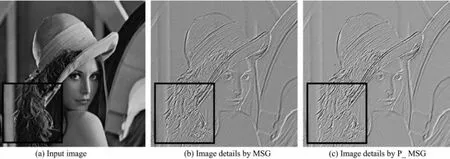
Fig.1 (a) the input image, (b) the decomposed image details by MSG after 6 iterations, and (c) the decomposed image details by P_MSG after 6 iterations. The squared area on the image is for the detailed comparison.

3 Image Enhancement with P_MSG Model

3.1 Enhancement for Gray Level Image

Histogram equalization (HE) is one of the most effective techniques for gray level image enhancement (Maini and Aggarwal, 2010), by which the global image contrast is virtually improved. But a deficiency associated with a few gray levels with some pixels might occur due to the quantization, and therefore some details might be lost during the enhancement. Since an underwater image is degraded by both the poor lighting condition and the scattering process, the dynamic range of the image gray levels is usually limited and the gray level values of pixel details are possibly spaced more closely. Thereby applying the histogram equalization to the original image could inevitably result in the loss of detailed image information. However, because the image structural decomposition fully preserves image details, the histogram equalization can be applied to the structure image component to correct the global image contrast.

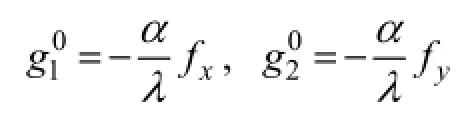
Fig.2 Experimental results. The left column is the input images. The middle column is the results by traditional histogram equalization. The right column is the results by the proposed method.

3.2 Color Image Enhancement

The Retinex algorithm has widely been used in color image enhancement. The principle of the algorithm is the so-called color constancy (Land, 1983), which has been assumed to agree with the perceptual channels of the human vision system. Since the principle was first proposed in 1971 (Land and McCann, 1971), the Retinex algorithm has been widely investigated and various approaches have been proposed to formulate the principle mathematically (Rahmanet al., 2004), the essence of which is to recover the intrinsic reflectivity of an object in color channels. The most favorited method is by far the multiscale Retinex (MSR) proposed by Rahmanet al., (1996), in which the reflectivity of an object is corrected through estimating the local illumination component. Assuming that an image is formulated in the following form：

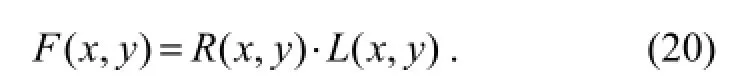
Through the logarithmic operation it can be simplified as：

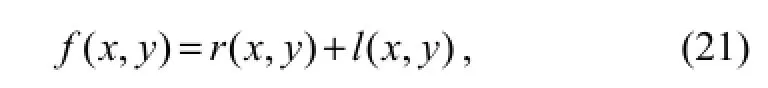
wherer(x,y)=log(R(x,y)) andl(x,y)=log(L(x,y)) are the reflectivity function and the illumination function, respectively. Because the illumination distribution is unknown (Orsiniet al., 2003; Zhanget al., 2011), the reflectivity component can be estimated by the model (Choiet al., 2007)

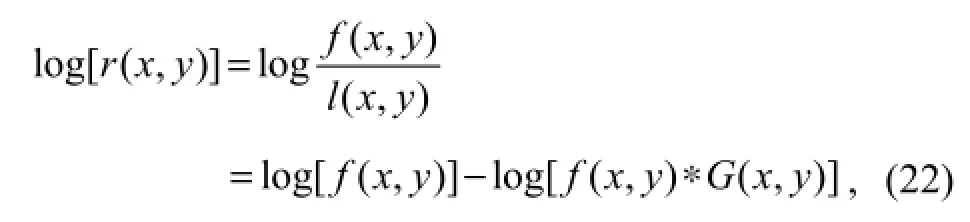
whereG(x,y) is the Gaussian operator. It should be noted that the estimate ofr(x,y) from Eq. (22) is in fact a locally averaged output related to the smoothing scale embedded in the Gaussian convolution. Therefore, for high frequency detailed components, inf(x,y), there could be the local ripple effect in the estimate ofr(x,y). However, the solution could improve the output with the image structural decomposition.

Without loss of component details, the Retinex method is applied to the structure image component after the decomposition with the P_MSG model. Assuming thatu(x,y) is the decomposed structure image, the follow equation is obtained

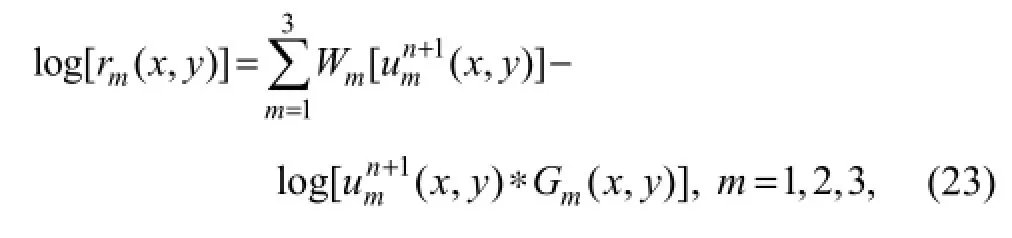
wherem=1, 2, 3, associated with the three chromatic channels, R, G, and B, respectively. The weightWm(m=1, 2, 3) is case-specific, and selected empirically. Here, however,Wm(m=1, 2, 3) can be reasonably determined by considering the optical absorption spectrum in water for different channels to further improve the color correction. The final output image can be expressed as

The proposed method was also applied for fog images, which was performed considering the same blurring mechanism as for underwater images. The results in Fig.4 show the improvement on the color correction.

4 Conclusions

Fig.3 Experimental results of underwater images. The left column is the input images. The middle column is the results by traditional MSR method. The right column is the results by the proposed method.

Fig.4 Experimental results of fog image. The left column is the input image. The middle column is the result by traditional MSR method. The right column is the result by the proposed method.

To improve underwater images that is degraded by the scattering and non-uniform illumination in water, an image enhancement approach, the P_MSG model, is proposed in this study based on the image structural decomposition. By introducing a curvature factor in the MSG decomposition algorithm, the decomposed component details and the structure component can be preserved without the gradient effect. Because image enhancement techniques are usually related to either global filter or local averaging operations, the distortion of the details after enhancement becomes inevitable due to the complexity of the image distribution. Since the color distortion and non-uniform illumination are represented by low-frequency components of images, image enhancement techniques, typically the histogram equalization and the Retinex algorithm, are merely applied for decomposed structure components in global image enhancement. The optical absorption spectrum in water medium is incorporated to improve the color correction as well. Finally, the enhanced structure and preserved component details are recomposed to generate the output. Thus, the proposed method can be effectively applied to improve the acquisitions of underwater images without the prior knowledge of image deconvolution.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 60772058 and 61271406). We would like to thank Prof. Guangrong Ji of the Ocean University of China for valuable discussion on mathematical topics.

Chen, J. J., Tian, F. C., and Can, L., 2011. Image restoration based on adaptive P-laplace diffusions.Image and Signal Processing, 37： 208-212.

Choi, D. H., Jang, I. H., Kim, M. H., and Kim, N. C., 2007. Color image enhancement based on single-scale retinex with a JND-based nonlinear filter. In：Circuits and Systems. 16th Ruropean Conference (EUSIPCO 2008), Lausanne, Switzerland, 3948-3951, DOI： 10.1109/ISCAS.2007.378664.

Dubreuil, M., Delrot, P., Leonard, I., Alfalou, A., Brosseau, C., and Dogariu, A., 2013. Exploring underwater target detection by imaging polarimetry and correlation techniques.Optical Society of America, 52 (5)： 997-1005.

Land, E. H., 1983. Recent advances in retinex theory and some implications for cortical computations： Color vision and the natural image.Proceedings of the National Academy of Sciences of the United States of America, 80 (16)： 5163-5169.

Land, E. H., and McCann, J. J., 1971. Lightness and retinex theory.Journal of the Optical Society of America, 61 (1)： 1-11.

Maini, R., and Aggarwal, H., 2010. A comprehensive review of image enhancement techniques.Journal of Computing, 2： 8-13.

Meyer, Y., 2001.Oscillating Patterns in Image Processing and Nonlinear Evolution Equations. American Mathematical Society, Boston, 71-91.

Morel, J. M., Petro, A. B., and Sbert, C., 2010. A PDE Formalization of Retinex Theory.IEEE Signal Processing, 19 (11)：2825-2837.

Mumford, D., and Shah, J., 1989. Boundary detection by minimizing functionals I. In：Image Understanding. Reprinted fromIEEE Proceedings on Computer Vision and Pattern Recognition (1985). Ablex Press, 22-26.

Orsini, G., Ramponi, G., Carrai, P., and Di Federico, R., 2003. A modified retinex for image contrast enhancement and dynamics control.Image Processing, 2 (3)： 393-396.

Rahman, Z., Jobson, D. J., and Woodell, G. A., 1996. Multiscale retinex for color rendition and dynamic range compression.SPIE Proceedings: Applications of Digital Image Processing XIX, 183： 183-191.

Rahman, Z., Jobson, D. J., and Woodell, G. A., 2004. Retinex processing for automatic image enhancement.Journal of Electronic Imaging, 13 (1)： 100-110.

Raimondo, S., and Silvia, C., 2010. Underwater image processing：State of the art of restoration and image enhancement methods.EURASIP Journal on Advances in Signal Processing 2010, 2010： 746052, DOI： 10.1155/2010/746062.

Strekalovskiy, E., Chambolle, A., and Cremers, D., 2012. A convex representation for the vectorial mumford-shah functional. In：Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE, Washington, DC, 1712-1719, DOI： 10.1109/CVPR.2012.6247866.

Wang, C., Fang, L., Ye, F. Q., and Ye, Z. F., 2008. Image cartoon-texture decomposition using Mumford-Shah Model and G-space.Journal of Data Acquisition & Processing, 23 (1)：17-22 (in Chinese with English abstract).

Zhang, K., Jin, W. Q., Su, Q., and Wang X., 2011. Multi-scale retinex enhancement algorithm on luminance channel of color underwater image.Infrared Technology, 3： 1003-1006 (in Chinese with English abstract).

(Edited by Xie Jun)

(Received June 21, 2013; revised August 29, 2013; accepted December 1, 2014)

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2015

* Corresponding author. Tel： 0086-532-66781215 E-mail： gywang@ouc.edu.cn