A Storm Surge Intensity Classification Based on Extreme Water Level and Concomitant Wave Height
2015-04-05DONGShengGAOJunguoLIXueWEIYongandWANGLiang
DONG Sheng, GAO Junguo, LI Xue WEI Yong, and WANG Liang
1)College of Engineering,Ocean University of China,Qingdao266100,P. R. China
2)The First Institute of Oceanography,SOS,Qingdao266061,P. R. China
3)Pacific Marine Environmental Laboratory,National Oceanic and Atmospheric Administration (NOAA), 98115,USA
4)Joint Institute for the Study of Atmosphere and Ocean,University of Washington,Seattle,WA98105,USA
A Storm Surge Intensity Classification Based on Extreme Water Level and Concomitant Wave Height
DONG Sheng1),*, GAO Junguo1),2), LI Xue1), WEI Yong3),4), and WANG Liang1)
1)College of Engineering,Ocean University of China,Qingdao266100,P. R. China
2)The First Institute of Oceanography,SOS,Qingdao266061,P. R. China
3)Pacific Marine Environmental Laboratory,National Oceanic and Atmospheric Administration (NOAA), 98115,USA
4)Joint Institute for the Study of Atmosphere and Ocean,University of Washington,Seattle,WA98105,USA
Storm surge is one of the predominant natural threats to coastal communities. Qingdao is located on the southern coast of the Shandong Peninsula in China. The storm surge disaster in Qingdao depends on various influencing factors such as the intensity, duration, and route of the passing typhoon, and thus a comprehensive understanding of natural coastal hazards is essential. In order to make up the defects of merely using the warning water level, this paper presents two statistical distribution models (Poisson Bi- variable Gumbel Logistic Distribution and Poisson Bi-variable Log-normal Distribution) to classify the intensity of storm surge. We emphasize the joint return period of typhoon-induced water levels and wave heights measured in the coastal area of Qingdao since 1949. The present study establishes a new criterion to classify the intensity grade of catastrophic storms using the typhoon surge estimated by the two models. A case study demonstrates that the new criterion is well defined in terms of probability concept, is easy to implement, and fits well the calculation of storm surge intensity. The procedures with the proposed statistical models would be useful for the disaster mitigation in other coastal areas influenced by typhoons.
storm surge; Poisson Bi-variable Gumbel Logistic distribution; Poisson Bi-variable Log-normal distribution; intensity classification; joint return period
1 Introduction
Offshore structures have been widely used in many areas of engineering, like ships, platforms, wind turbines, oil productions and temporary storage of recovered liquids. So far, most of the offshore structures have been limited to fixed platforms in shallow-water areas. In deeper water, floating structures may be more feasible. However, the design of floating structures to survive extreme events is more complicated than that of fixed platforms. It requires knowledge and methods to treat complex problems of fluid-structure interactions in severe seas, like large waveinduced motions and distorted free surface. Therefore, it is important to carry out an integrated analysis for floating structures. However, thus far only limited studies have been performed (Grecoet al., 2009; Honget al., 2004; Koo and Kim, 2005). In the present study, a CFD model has been developed for the coupled dynamic analysis of an offshore floating oil storage tank in surging waves.
Storm surge from typhoon is one of the main naturalthreats to coastal communities. It occurs frequently and usually results in the most serious economic loss among all the natural hazards in China. Along with the development of the coastal area, storm surge is becoming one of the main natural disasters that significantly hinder the economic growth and social progress. Similarly, the United States of America (USA) has experienced several severe hurricanes since 2004, such as Hurricane Ike, Rita, Katrina, and Ivan. All of these hurricanes produced storm surge reaching or exceeding previous records, and such topics have immediately become a research focus for disaster mitigation and prevention.
Seawalls are the primary coastal protection facilities, and their protection standard can be established using return periods of the design tidal level (or water level) and design wave. In China, two existing methods are currently used to combine the return periods of tidal level and wave climate. One is the adoption of different return period of tidal level and wave height. Another is the adoption of the same return period of tidal level and wave height under the condition that these two marine environmental factors are independent. Actually a general approach is to employ a same return period for both tides and waves, for instance in Fujian Province. However, it may lead to excessively conservative design criteria.Tides and wave climate are relative, and a joint design criterion considering both of the two environmental parameters may enhance the interpretation of the actual storm process.
How to calculate the storm surge intensity and estimate the magnitude of storm surge disaster is one of the main research topics in surge prevention and seawall design. For the past 40 years, scientists of coastal study have been using the Saffir-Simpson Scale to classify tropical cyclones (Dolan and Davis, 1994). Halsey (1986) proposed a classification of Atlantic Coast extratropical storms based on damage potential index. Mendoza and Jiménez (2005) provided a storm classification based on the beach erosion potential in Catalonian Coast. At present, there exist several kinds of grade classification of storm surge in China: 1) Intensity grade based on the set-up caused by the storm surge (Gan, 1991), 2) Intensity grade based on the extreme total water level (Xu and Tan, 1998), 3) Disaster degree grade based on disaster damage (Shiet al., 2000). The first method considers the storm set-up as a primary factor in measuring the hazardous level caused by storm surge. The second method uses the total water level, which includes both the storm set-up and the joint effect of the astronomical tide and flood, with various coefficients as the criterion. The third method establishes the corresponding disaster degree grade in terms of disaster-resulting loss. The loss due to storm surge includes direct loss (such as loss of life and property) and indirect loss (such as repair and reconstruction, disaster relief, and influence on ecological environment). The direct loss mainly depends on the storm surge intensity and its influencing area, while the latter is related to the economic development level, topography, and the ability of disaster prevention. Technically, the third method takes into account of the total impact from a storm surge event. Up to now such a standard statistics has not been established in China. The reliability of statistics in the investigation of disasters can greatly affect the accuracy when the third method is used.
Besides the methods mentioned above, Xu and Tan (1998) discussed the relationship between the intensity and the disaster degree of the typhoon-induced storm surge. Le (1998) suggested that the damage of the storm surge disaster should not be considered as the same as that of the typhoon disaster, although typhoon is the primary cause of storm surge. As a matter of fact, the damage caused by storm surge can be easily distinguished from that directly caused by the strong wind during a typhoon event. The damage caused by seawater flooding can be defined as storm surge disaster in principle. More and more researches show that serious storm surge damages are mostly caused by the concurrence of high tide and large waves along the shoreline (Li, 1998). However, the first and second grading methods only take account of water set-up or total tide level. The water level used in the second grading method is also named warning water level. When the total tidal level exceeds this critical water level, disaster prevention measures will be taken to mitigate the storm surge-induced economic loss by the local government. Since this warning water level only includes the influence of wave set-up and the astronomical tide but ignores the concurrent storm waves, it is not a correct measure of the overall magnitude of the storm surge. The storm surge disaster magnitude needs to be identified correctly before a relationship between the storm surge intensity and disaster degree is established.
Bivariate extreme value distribution is a basis to estimate the joint return value of oceanic environmental parameters. Leira (2010) studied some bivariate Weibull distributions for two dimensional statistical analyses. Heffernan and Tawn (2004) proposed an entire new semiparametric approach of the joint distributioncapable of consisting of both asymptotically independent and asymptotically dependent variables. Jonathanet al. (2010) applied this model to fit the joint distribution of significant wave height and wave peak period. Myrhaug and Leira (2011) introduced a bivariate Fréchet distribution, and applied it to estimate the probability of two successive spilling breakers and two successive plunging breakers on different bottom slopes by using wave parameters corresponding to typical field conditions. In 2004, Zhang and Xu (2005) derived a maximum entropy probability distribution of significant wave heights. Donget al. (2012) proposed a bivariate equivalent maximum entropy distribution to estimate joint design parameters for the concomitant wave height and wind speed at a site in the Bohai Sea. Donget al. (2013) also used this model to study the asymptotical relations of extreme values of the joint significant wave height and peak wave period.
This paper proposes a new method to classify storm surge intensity based on two bi-variable compound extreme distribution models: Poisson Bi-variable Gumbel Logistic Distribution (PBGLD) and Poisson Bi-variable Log-normal Distribution (PBLD). We illustrate this new method using observed tidal level and the corresponding wave height series from typhoon processes in the coastal area of Qingdao, China, considering the occurrence frequency of typhoon and the defects of the warning water level. This new method emphasizes on the joint return period of water levels and synchronized wave heights using observations collected from historical typhoons in the coast of Qingdao since 1949. A novel criterion is put forward to grade the intensity of typhoon-induced storm surge, forming a basis to evaluate the storm surge intensity for seawall design.
2 Typhoon-Induced Storm Surge in Qingdao
Qingdao is located on the southern coast of the Shandong Peninsula (35°35´N-37°09´N, 119°30´E-121°00´E, Fig.1). Between 1949 and 2001, 77 typhoons affected Qingdao with their centers passing the area north to 35°N, averaging three times every two years. Statistics shows that 87.1% of these typhoons occurred between July and September, and 39% of them in August (Fig.2). Although 1.5 typhoons affect Qingdao annually, typhoon-induced surge does not occur every year. In Qingdao, the disasterintensity of a storm surge is influenced by various factors, such as intensity, duration, and route of the passing typhoon. When strong storm surge coincides with high astronomical tide, the resulting water level along the coastline can be dangerous enough to cause serious damages to the coastal infrastructure.

Fig.1 Location of Qingdao City.
More than ten typhoon surges have affected the Qingdao area since 1980, and three of them caused serious impact to the local economic development. Table 1 shows the duration, wind and wave conditions, and the direct economic loss of the three typhoons.
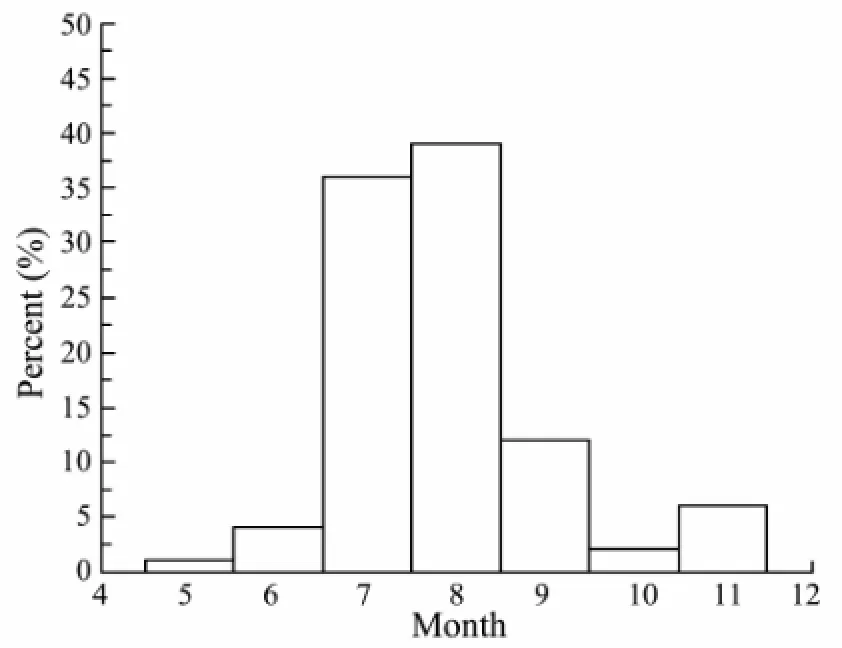
Fig.2 Typhoon monthly occurrence distribution in Qingdao area.

Table 1 Three most serious typhoon surge disasters in Qingdao area
3 Poisson Bi-variable Compound Distributions
Single variable compound extreme distribution has been extensively applied in coastal and offshore engineering in China (Liu, 1982; Langley and El-Shaarawi, 1986; Donget al., 2000; Donget al., 2003) since it was first established in Liu and Ma (1980). Liuet al., (2002) derived a Poisson Bi-variable Compound Gumbel distribution to estimate the joint impact of typhoon winds and concomitant waves on oil platform in the East China Sea. Donget al. (2005) presented a Poisson Bivariate Log- normal Distribution to determine different design criteria of ocean environmental conditions. Donget al. (2008) utilized the Bi-variable Pearson Type III distribution to estimate the joint return values of extreme wind speed and its associated wave height. The present study proposes two Poisson bi-variable compound distributions to provide statistical analysis of the extreme water level and concurrent wave height, which leads to a new method for classifying the intensity of typhoon-generated storm surge.
Assume that the yearly occurrence frequencynof typhoon in Qingdao is a discrete random variable and its distribution probability can be expressed asPk, wherek= 0, 1,…,n. Let (ξ,η) represent the extreme water level and the corresponding wave height under the surge condition, and (ζ,γ) be the same quantities under the condition of no surge. Assuming that (ξ,η) and (ζ,γ) are two dimensional continuous random variables, we can useG(x,y) andQ(x,y) to describe their joint distribution functions, respectively. The joint probability density function of (ξ,η) isg(x,y), and the distribution function ofξisGx(x). Let (ξi,ηi) be theith observation value andna non-negative integral random variable independent of (ξ,η), then the distribution function of (ξi,ηi) can then be defined as
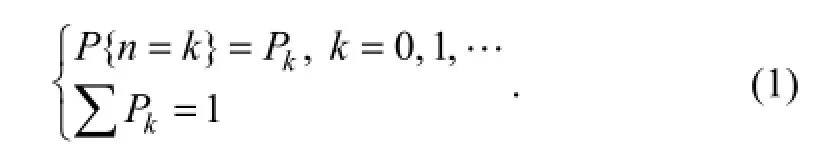
Random vectors (X,Y) are defined as:

Therefore,
Eq. (3) is named the bi-variable compound extreme distribution composed of discrete distributionPkand continuous distributionG(x,y) (Liuet al., 2002).
In the coastal area of Qingdao, the tide levelζand the corresponding waveγare generally small when storm surge is not present. One can see that (ζ0,γ0) must exist so that they satisfyP{(ζ〉ζ0)∪(γ〉γ0)}=0, namelyQ(x,y)=1. Suppose that the occurrence frequencynof typhoon agrees with the Poisson distribution, andλis the occurrence number of typhoon, then the bi-variable compound extreme distribution (3) can be expressed as:

Assume that the bi-variable continuous distributionG(x,y) agrees with PBGLD or PBLD, and the correspondingGx(x) follows Gumbel distribution or Log-normal distribution.
3.1 Poisson Bi-variable Gumbel Logistic Distribution (PBGLD)
Gumbel (1960) showed that the marginal probability density functions of random variablexandyof PBGLD can be expressed as:
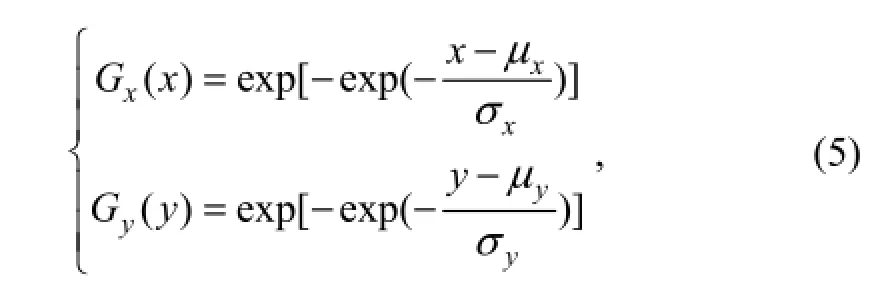
whereμxandσxare the location and scale parameters of the Gumbel distribution for the random variable seriesxi(i=1, 2,…,n), andμy,σyare the location and scale parameters of the Gumbel distribution for random variable seriesyi(i=1, 2…,n). The joint probability density function ofxandyis expressed as follows:

3.2 Poisson Bi-variable Log-Normal Distribution (PBLD)
The marginal probability density functions of random variablexandyof PBLD are expressed as follows (Papoulis, 1991):

whereμxandσxare the mean and variance of the random variable series ofx(lnxi,i=1, 2…,n), andμyandσyare the mean and variance of random variable series ofy(lnyi,i=1, 2…,n). The joint probability density function ofxandycan then be expressed as follows:
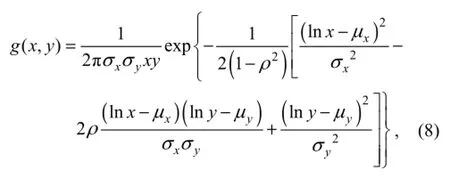
whereρis the correlation coefficient. By substituting Eq. (8) into Eq. (4), the Poisson Bi-variable Log-normal distribution can be obtained.
With Eq. (6) and Eq. (8) being the joint probability density functions, the joint occurrence probabilityPunder the conditions ofx≥uandy≥vis given by
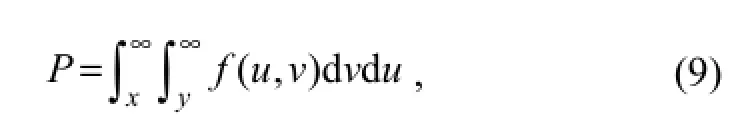
wheref(·, ·) is the joint probability density function ofF(·, ·) by Eq. (4).
The reciprocal ofPis the joint return periodTcorresponding toP.
4 Distribution of Disastrous Typhoon-Induced Storm Surge
Demonstrated in Fig.3 are the observed records of tidal level and concomitant wave height collected from typhoons in the coastal area of Qingdao since 1949 (Li, 1998). We select the extreme annual water level and the corresponding wave height as a bivariate statistical sample. The occurrence frequency numbernof typhoon agrees with the Poisson distribution at the 0.05 significance level byχ2test (Papoulis, 1991), as seen in Fig.4 (fitting curve of theχ2distribution matches the histogram well), the vertical axis denoting the numbers of disastrous typhooninduced storms every year.
4.1 PBGLD of Disastrous Storm Surge
The K-S test indicates that the fitting of water level and wave height agrees with the Gumbel distribution at the 0.05 confidence level (Table 2 and Fig.5).
Estimated by the Gumbel distribution of extreme water level, the 50-year return value caused by the storm surgeis 5.61 m. Fig.6 indicates that the most probable wave height that may occur in Qingdao is 3.5 m. Fig.7 shows the contours of the joint probability of water level and wave height obtained from the PBGLD model, and the values 0.01, 0.02, 0.05, 0.1 and 0.2 on the curves being the joint return probabilities of water level and wave height, respectively. For instance, when the extreme water level reaches 5.25 m, the warning water level of Qingdao, the probabilities for the associated wave heights 3.0, 4.0, 5.0 and 6.0 m to occur are 4.5%, 2.9%, 1.7%, and 0.9%, respectively. Therefore, the concept of a warning water level can hardly reflect the recurrence feature of a disastrous storm surge.

Table 2 K-S tests about fitting of water level and wave height (Gumbel distributions)
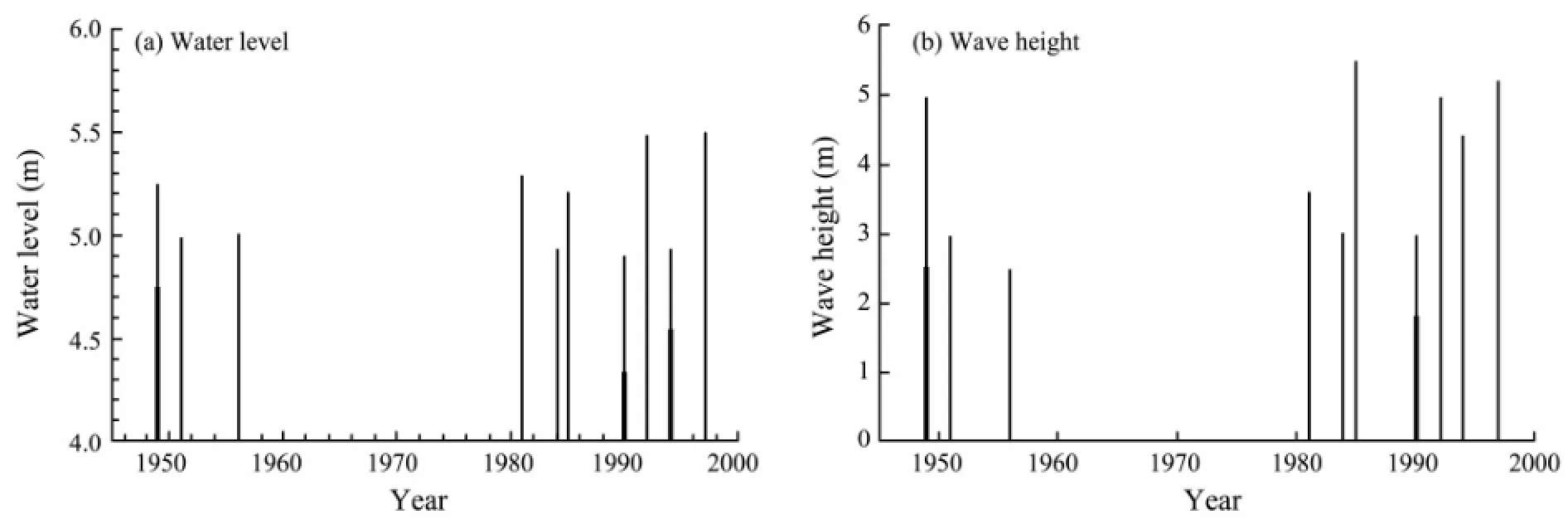
Fig.3 Observed extreme water level and wave height during each storm process.
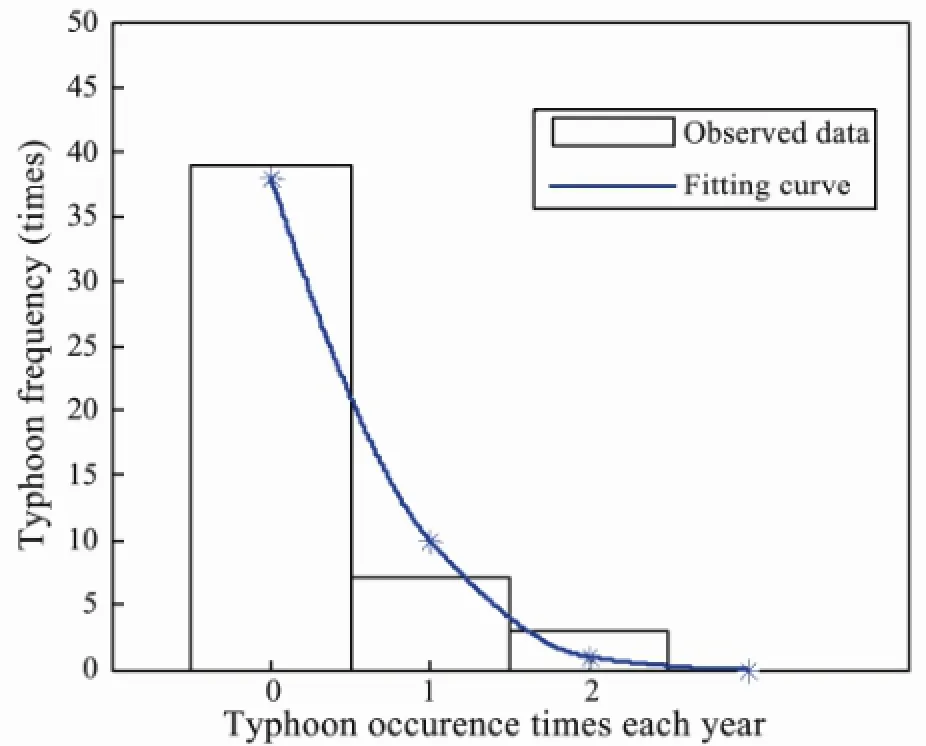
Fig.4 Poisson distribution of typhoon frequency.
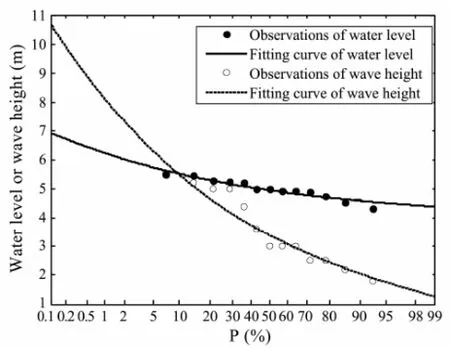
Fig.5 Gumbel distribution of water level and wave height.

Fig.6 Conditional and marginal prob. density curve.
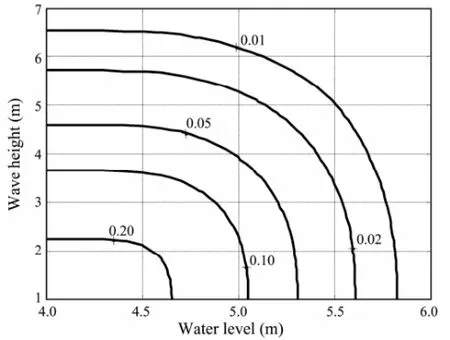
Fig.7 Joint probability contour.
4.2 PBLD of Disastrous Storm Surge
The K-S test indicates that the water level and associated wave height agree with the Log-normal distribution at the 0.05 confidence level (Table 3 and Fig.8).
Given the 50-year return water level caused by storm surge is 5.76 m, Fig.9 indicates that the most probable wave height that may occur in Qingdao is 3 m. Fig.10 shows the contours of the joint probability of water level and wave height obtained from the PBLD, and the values 0.01, 0.02, 0.05, 0.1 and 0.2 on the curves are the joint return probability of water level and wave height, respectively. When the extreme water level reaches 5.25 m, the warning level of Qingdao, the probabilities of associated wave height 3.0, 4.0, 5.0 and 6.0 m to occur are 4.9%, 3.0%, 1.6% and 0.81 %, respectively.
Comparison between Tables 2 and 3 shows that Lognormal distribution fits better than Gumbel distribution for the data of extreme water level, but for wave height, fitting by Gumbel distribution is preferred. Joint distributions with different marginal distributions can be constructed by copulas, but it is not what to be researched here.

Table 3 K-S tests about fittings of water level and waveheight (Log-normal distributions)
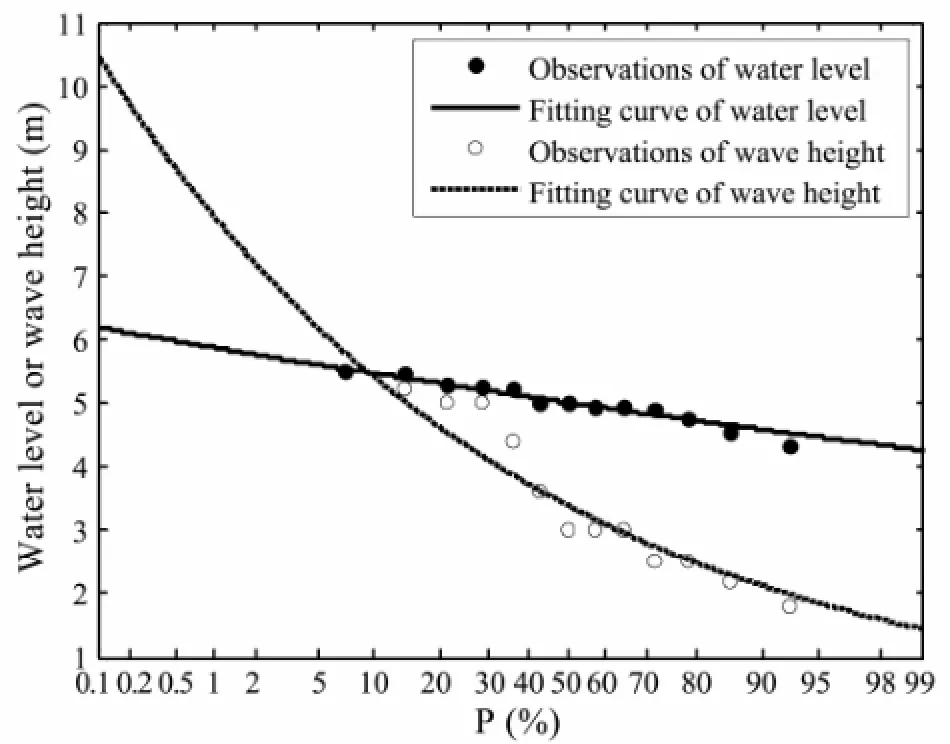
Fig.8 Log-normal distribution of water level and wave height.
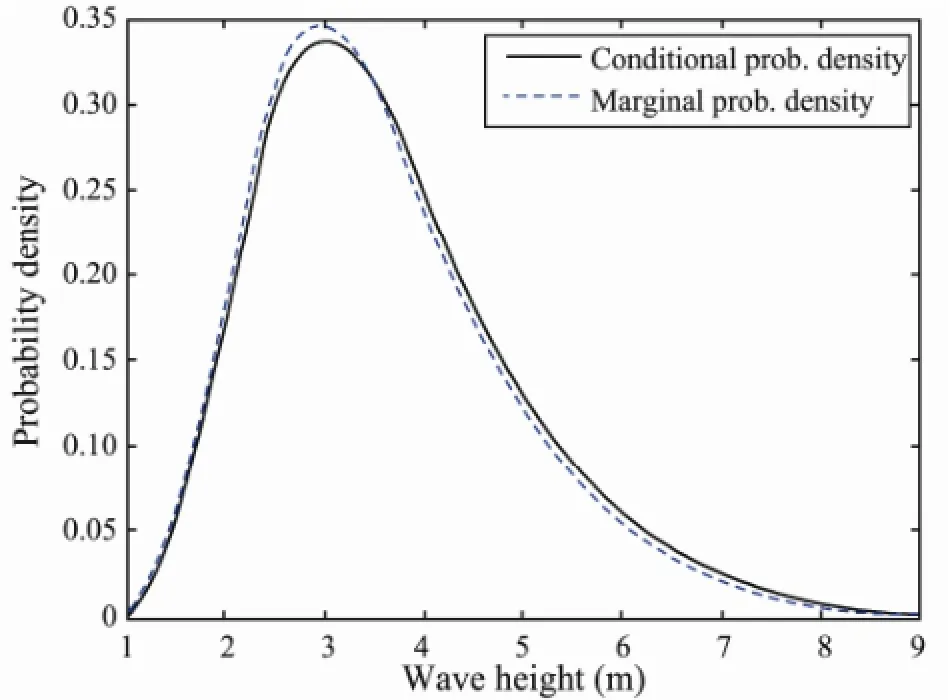
Fig.9 Conditional and marginal prob. density curve.
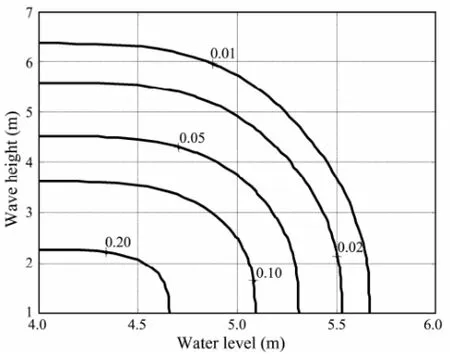
Fig.10 Joint probability contour.
4.3 Grade of Typhoon-Induced Storm Surge Intensity
Based on the joint return period of the extreme water level and concomitant wave height, we propose a novel classification of storm surge intensity grade (see Table 4).

Table 4 Grade of typhoon surge intensity
The joint return periods and corresponding surge intensity of typhoon surge disasters in Qingdao since 1949 have been calculated with the two bi-variable compound extreme distributions and listed in Table 5.
As verification of the computed results of the two models, the typhoon surge disaster grades by Li (1998) and Guoet al. (1998) are listed in Table 5. One can see that the new classification of storm surge intensity based on PBGLD or PBLD return period is mostly consistent with the statistical disaster rank. Among the thirteen storm surge events, No. 9415 is indicated as a ‘moderate’event by both PBGLD and PBLD methods while the disaster statistics graded it as a ‘mild’ event. The two joint distributions (PBGLD and PBLD) predict very close return periods, 18 years and 17 years, for the No. 9415 event. Owing to increasing awareness of disaster mitigation after typhoon 9216, the loss of typhoon 9415 became a lot less due to timely evacuation and had made it a‘mild’ event in the statistical disaster rank. It is worth noting that both PBGLD and PBLD provide statistical analysis of natural characteristics of the typhoon event but contain no information of the associated social impact. The return periods predicted by PBGLD and PBLD agree with each other for most of the surge events listed in Table 5, with a difference of only 1 to 2 years.
By comparing the two distribution models, we find that:1) for surge events that are below the catastrophic intensity, the joint return period predicted by PBGLD model is1 to 2 years longer than that predicted by PBLD model; 2) for surge events that are ‘catastrophic’, the joint return period predicted by PBLD model, however, is much longer than that predicted by PBGLD model.
Table 5 indicates that high extreme water level combined with large wave height may result in ‘severe’ storm surge event, such as No. 9711, No. 9216 and No. 8509), while a combination of high extreme water level and small wave height tends to cause a ‘mild’ surge event, such as No. 4908. Furthermore, this statistical phenomenon confirms the hypothesis that serious typhoon surge in Qingdao area are caused by the simultaneous occurrence of high tidal level and large wave heights at the shoreline.
From Table 5, it is worth noting that the warning water level does not take account of the overall intensity of the storm surge. Taking events No. 4908, No. 8114 and No. 8509 as examples, the highest water levels of these three events are almost the same: 525 cm for No. 4908, 529 cm for No. 8114 and 521 cm for No. 8509, while they are classified as ‘moderate’, ‘severe’ and ‘catastrophic’, respectively, based on the new methods proposed in this study. The main reason is that different wave heights, as well as the different joint return periods of water level and wave height, occurred in these events. The methods presented here are feasible and realistic approaches to determine the intensity of the disastrous storm surge.

Table 5 Disaster-induced intensity of typhoon surge in Qingdao area
5 Conclusions
Two bi-variable compound extreme distribution models, PBGLD and PBLD, are applied to provide a new classification for the intensity of typhoon-induced storm surge. This new approach fully considers the magnitude of storm surge, the joint distribution of two extreme environmental variables, and the occurrence frequency of a typhoon, so it can overcome the defects of merely using the warning water level. With the new distribution models, this study provides an estimate of the joint return period for many typhoon events between 1949 and 2001 based on the observations of tidal level and associated wave height in typhoon processes in the coastal area of Qingdao. A new criterion is put forward to classify the intensity grade of disastrous storm surge. The case studies indicate that the new criterion gives an explicit notion in terms of joint probability that is easy to manipulate and fits well the classification of the surge intensity. The proposed method of storm surge classification using new statistical model can be adopted as a reference approach in many coastal areas affected by typhoon. The data used here is limited; it is recommended that the proposed method should only be used for reference, and more verification and improvement are needed for broader application.
Acknowledgements
The study is supported by the National Natural Science Foundation of China (Nos. 51279186, 51479183), the National Program on Key Basic Research Project (2011 CB013704), the 111 Project (B14028), and the Marine and Fishery Information Center Project of Jiangsu Province (SJC201411 0338).
Dolan, R., and Davis, R. E., 1994. Coastal storm hazards.Journal of Coastal Research, Special Issue (12): 103-114.
Dong, S., Fan, D. Q., and Tao, S. S., 2012. Joint occurrence period of wind speed and wave height based on both service term and risk probability.Journal of Ocean University of China, 11 (4): 488-494.
Dong, S., Li, F. L., and Sun, R. W., 2000. On the peak over threshold method in the statistical analysis of storm surge elevation and its probability model.Periodical of Ocean University of Qingdao, 30 (3): 542-548 (in Chinese).
Dong, S., Liu, W., and Xu, P. J., 2008. Combination criteria of joint extreme significant wave height and wind speed at Weizhoudao offshore area.The Proceedings of 27th International Conference on Offshore Mechanics and Polar Engineering, Estoril, Portugal, OMAE57219.
Dong, S., Liu, Y. K., and Wei, Y., 2005. Combined return values estimation of wind speed and wave height with Poisson Bi-variable Log-normal distribution.The Proceedings of 15th International Offshore and Polar Engineering Conference, Seoul, Korea, III, 435-439.
Dong, S., Wang, N. N., Liu, W., and Guedes Soares, C., 2013. Bivariate maximum entropy distribution of significant wave height and peak period.Ocean Engineering, 59: 86-99.
Dong, S., Wei, Y., Hao, X. L., and Liu, D. F., 2003. Extreme prediction of storm surge elevation related to seasonal variation.The Proceedings of 13th International Offshore and Polar Engineering Conference, Hawaii, USA, IV, 878-883.
Gan, Y. M., 1991. Identification and judgment of disaster extent of typhoon storm surge.Proceedings of Disaster Prevention and Development Along Coastal Area of China. Earthquake Publishing House, 322-327.
Greco, M., Colicchio, G., and Faltinsen, O. M., 2009. Bottom slamming for a very large floating structure: Coupled global and slamming analyses.Journal of Fluids and Structures, 25:420-430.
Gumbel, E. J., 1960. Multivariate extreme distributions.Bulletin of the International Statistical Institute, 39 (2): 471-475.
Guo, K. C., Guo, M. K., Jiang, C. B., and Yan, S., 1998. Preliminary analysis of disaster caused by Typhoon No.9711 in Shandong Peninsula of China.Marine Forecasts, 15 (2): 47-51 (in Chinese).
Halsey, S. D., 1986. Proposed classification scale for major Northeast storms: East Coast USA, based on extent of damage.Geological Society of America, Abstracts with Programs(Northeastern Section), 18: 21.
Heffernan, J. E., and Tawn, J. A., 2004. A conditional approach for multivariate extreme values.Journal of the Royal Statistical Society: Series B, 66: 497-531.
Hong, D. C., Hong, S. Y., and Hong, S. W., 2004. Numerical study on the reverse drift force of floating BBDB wave energy absorbers.Ocean Engineering, 31: 1257-1294.
Jonathan, P., Flynn, J., and Ewans, K. C., 2010. Joint modelling of wave spectral parameters for extreme sea states.Ocean Engineering, 37: 1070-1080.
Koo, B. J., and Kim, M. H., 2005. Hydrodynamic interactions and relative motions of two floating platforms with mooring lines in side-by-side offloading operation.Applied Ocean Research, 27: 292-310.
Langley, R. M., and El-Shaarawi, A. H., 1986. On the calculation of extreme wave heights: A review.Ocean Engineering, 13 (1): 93-118.
Le, K. T., 1998. Basic problems of risk evaluating method for storm surge disaster.Marine Forecasts, 15 (3): 38-44 (in Chinese).
Leira, B. J., 2010. A comparison of some multivariate Weibull distributions.Proceedings of the 29th International Conference on Offshore Mechanics and Arctic Engineering, OMAE-20678, Shanghai, China, ASME, 2010.
Li, P. S., 1998. Study of typhoon storm surge disaster forecasting method.Marine Forecasts, 15 (3): 72-78 (in Chinese).
Liu, D. F., 1982. Long-term distribution of hurricane characteristic.Proceedings of 12th Offshore Technology Conference, OTC4325, 182.
Liu, D. F., Wen, S. Q., and Wang, L. P., 2002. Poisson-Gumbel Mixed compound distribution and its application.Chinese Science Bulletin, 47 (22): 1901-1906.
Liu, T. F., and Ma, F. S., 1980. Prediction of extreme wave heights and wind velocities.Journal of the Waterway Port Coastal and Ocean Division, 106 (4): 469-479.
Mendoza, E. T., and Jiménez, J. A., 2005. A storm classification based on the beach erosion potential in the Catalonian coast.Coastal Dynamics, 3: 1-11.
Myrhaug, D., and Leira, B. J., 2011. A bivariate Fréchet distribution and its application to the statistics of two successive surf parameters.Proceedings of the Institute Mechanical Engineers, Part M., Journal of Engineering for the Maritime Environment, 225 (1): 67-74.
Papoulis, A., 1991.Probability, Random Variables, and Stochastic Processes. McGraw-Hill, Inc., 124-150.
Shi, J. H., Wang, M. W., Wang, Y. X., Yu, B., and Xia, Z. W., 2000. Study of grade classification of storm surge disaster.Marine Forecasts, 17 (2): 12-15 (in Chinese).
Xu, Q. W., and Tan, S. D., 1998. Research on the method of evaluating the economic loss caused by storm surge disaster.Marine Science Bulletin, 17 (1): 1-12 (in Chinese).
Zhang, L. Z., and Xu, D. L., 2005. A new maximum entropy probability function for the surface elevation of nonlinear sea waves.China Ocean Engineering, 19 (4): 637-646.
(Edited by Xie Jun)
(Received March 22, 2013; revised May 6, 2013; accepted May 21, 2014)
© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2015
* Corresponding author. Tel: 0086-532-66781125 E-mail: dongsh@ouc.edu.cn
杂志排行
Journal of Ocean University of China的其它文章
- Impacts of the Two Types of El Niño on Pacific Tropical Cyclone Activity
- Numerical Simulation of Typhoon Muifa (2011) Using a Coupled Ocean-Atmosphere-Wave-Sediment Transport (COAWST) Modeling System
- Estimating the Turbulence Characteristics in the Bottom Boundary Layer of Monterey Canyon
- Composition and Origin of Ferromanganese Crusts from Equatorial Western Pacific Seamounts
- Hydroelastic Analysis of a Very Large Floating Structure Edged with a Pair of Submerged Horizontal Plates
- Synergetic Analysis and Possible Control of Vortex-Induced Vibrations in a Fluid-Conveying Steel Catenary Riser
