使用融合乘加加速快速傅里叶变换计算的向量化方法*

刘 仲，陈海燕，向宏卫

(国防科技大学计算机学院，湖南长沙 410073)

现有的许多处理器体系结构提供融合乘加(Fused Multiply-Add，FMA)指令，如 Intel的Itanium，IBM的Power处理器等。给定3个输入操作数a，b，c，使用一条FMA指令即可实现y=±a±(b×c)中的任何一个操作。FMA指令对于数值计算亦具有重要的意义。因为，在软件上，一条FMA指令在执行时间上和一条乘法或加法指令几乎一样快;在硬件上，FMA单元通常比分开的乘法器和加法器耗费少;在计算上，FMA指令通过减少舍入操作可以提高数值计算精度。在提供FMA指令的处理器平台上，对于有些数值计算应用，转换到FMA指令是比较直接的，如普通的矩阵和向量乘法、矩阵和矩阵乘法以及成对出现的乘法和加法操作计算。但是，对更多的其他应用就没有那么简单了，需要平衡加法和乘法操作，改造原有的计算方法或流程以适合FMA指令，才能充分发挥FMA指令的作用，加速计算的性能。

向量处理器在单个芯片上集成多个向量处理单元(Vector Processing Element，VPE)，每个 VPE包含相同的MAC，ALU，BP等多个功能部件，能够在降低面积和功耗的情况下大幅提高整芯片的计算能力，适合处理高密集运算的任务，如矩阵计算、FFT运算、滤波运算等。然而，现有的大量程序和算法是基于单核处理器设计的，很多高密集运算的任务由于算法本身的特性，向量化处理困难，如何针对向量处理器的多运算部件的向量计算的体系结构特点，充分开发各个层次的并行性，高效地向量化这些算法是当前面临的主要困难［1-2］。

快速傅里叶变换(Fast Fourier Transform，FFT)作为时域和频域的基本变换工具，在现代信号处理系统领域应用广泛，如雷达、声呐、地震信号分析、频谱分析、语音识别、3G通信和图像处理等。FFT能显著减少离散傅里叶变换(Discrete Fourier Transform，DFT)计算的复杂度，对于实时性要求很高的信号处理应用来说，DFT计算效率越高，信号处理的实时性就越好，因此FFT算法的优化方法一直是国内外的研究热点。Pease［3］采用数学工具Kronecker积描述FFT算法，方便将FFT算法高效地映射到并行计算机上;Linzer［4］，Goedecker［5］和 Karner［6］等针对 FMA 结构的处理器，分别研究了如何利用FMA指令优化FFT计算;Voronenko［7］依据有向无环图和具有一定结构的矩阵因子化算法，提出一种将离散傅里叶变换、离散余弦变换等线性变换转化为FMA算法的一般方法;FFTW(Fastest Fourier Transform in theWest)［8］是通用CPU平台上广泛使用的FFT数学库，移植性好，可以为任意长度和维数的FFT自动生成一种最有效的实现方式;Loberiras［9］等针对GPU提出小点数FFT的优化技术，受限于纹理存储器的大小，大点数 FFT的性能不理想;Li［10］等针对 GPU提出一种 FFT自适应优化框架，当点数大于1K时，获得接近CUDA快速傅里叶变换(CUDA Fast Fourier Transform，CUFFT)的90%性能;文献［11］针对GPU的大点数FFT优化方法达到CUFFT性能的2．1倍。

在传统的FFT计算中，蝶形单元的最终计算往往转化为实数的乘法和加法操作，如时域抽取基2 FFT算法的一个蝶形单元计算需要4次实数乘法和6次实数加法，即需要10次实数乘(加)操作;时域抽取基4 FFT算法的一个蝶形单元计算需要12次实数乘法和22次实数加法，即需要34次实数乘(加)操作。显然，FFT计算中的乘、加操作是不平衡的，不能直接利用FMA指令来实现蝶形单元的计算，所以传统的FFT计算方法不能有效发挥具有FMA指令的处理器的计算效率。刘仲等针对FMA结构的向量处理器，提出一种基于FMA加速FFT计算的向量化方法，通过变换FFT的蝶形单元运算流程，将传统计算方式中的独立的乘法和加法操作组合成次数更少的FMA操作，使得计算一个DIT基2 FFT算法的蝶形单元所需要的浮点操作减少到6次FMA操作，计算一个DIT基4 FFT算法的蝶形单元所需要的浮点操作减少到24次FMA操作。实验结果表明，提出的方法能够显著加速FFT的计算性能。

1 向量处理器Matrix的体系结构

如图1所示，Matrix是一款面向高密度计算应用的高性能浮点向量处理器，内核是超长指令字(Very Long Instruction Word，VLIW)体系结构，包括标量处理部件(Scalar Processing Unit，SPU)和向量处理部件(Vector Processing Unit，VPU)。SPU负责标量任务计算和流控，SPU和VPU可通过共享寄存器交换数据。Matrix每时钟周期发射11条指令，包括5条标量指令和6条向量指令。指令派发单元对执行包进行识别，并将其中的指令派发到相应的功能单元中执行。VPU负责向量计算，包括16个向量处理单元(Vector Processing Element，VPE)，每个VPE含一个局部寄存器文件，以及3个浮点乘加单元(Float Multiply and Accumulate，FMAC)、1个BP和2个L/S共6个并行功能部件，3个FMAC均支持FMA指令。局部寄存器文件包含64个64位寄存器，所有VPE的同一编号的局部寄存器在逻辑上又组成一个1024位的向量寄存器。功能部件支持定点和浮点操作，向量指令在各个VPE上同时独立运行。向量数据访问单元支持向量数据的Load/Store，提供大容量阵列向量存储器(Array Memory，AM)，每周期同时支持2个Load/Store指令。

图1 Matrix的体系结构Fig．1 Architecture of Matrix

2 基于FMA的FFT向量化优化方法

序列x(n)(n=0，…，N-1)的离散傅里叶变换 X(k)(k=0，…，N-1)定义为:

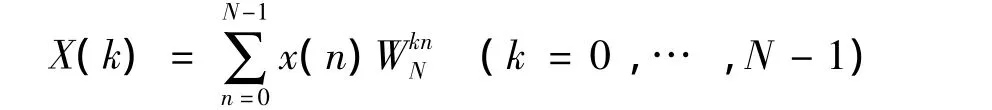
依据离散傅里叶变换公式计算的DFT复数乘加运算的计算复杂度是N2。当N比较大时，运算量增长得非常快，使得直接采用DFT计算方法难以满足很多实际应用的需求。1965年Cooley和Turkey提出一种快速傅里叶变换算法［12］，计算复杂度由原来的O(N2)降到O(N log2N)，可显著地减少运算量。FFT算法分为时间抽取法(Decimation In Time，DIT)和频率抽取法(Decimation In Frequency，DIF)两种，现以 DIT 方法为例阐述FFT的向量化方法。

2．1 传统的FFT蝶形单元计算方法

2．1．1 DIT基2FFT的蝶形单元计算方法

当N是2的整数次方时，DIT基2FFT将输入数据序列x(n)进行奇、偶分组:

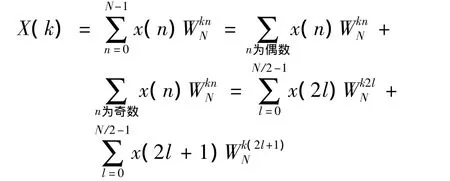
由旋转因子的周期性特性易知:

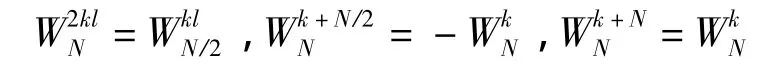
令 a(l)=x(2l)，b(l)=x(2l+1)，则序列X(k)划分为2个长度为N/2的子序列:

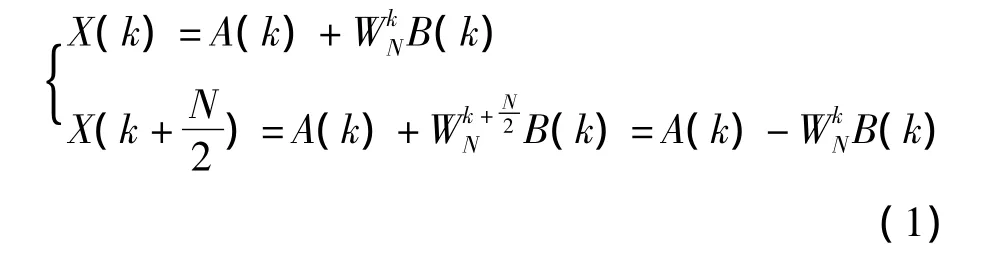
图2是DIT基2FFT的蝶形单元运算流程图，DIT基2FFT的每次蝶形单元运算需要1次复数乘法，2次复数加法，转变实数计算即为4次实数乘法和6次实数加法，即需要10次实数乘(加)操作。

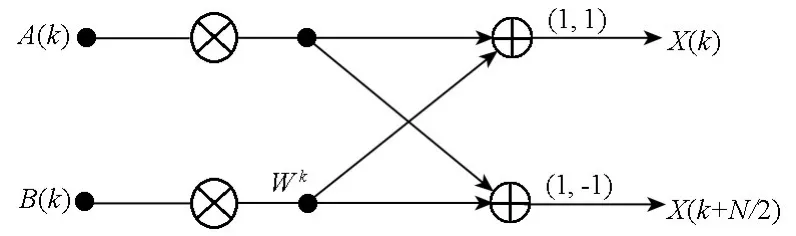
图2 DIT基2 FFT的蝶形单元运算流程图Fig．2 Radix-2 DIT FFT butterfly diagram

2．1．2 DIT基4FFT的蝶形单元计算方法

当N是4的整数次方时，DIT基4FFT将输入数据序列x(n)按模4后的余数分组:

由旋转因子的周期性特性易知:

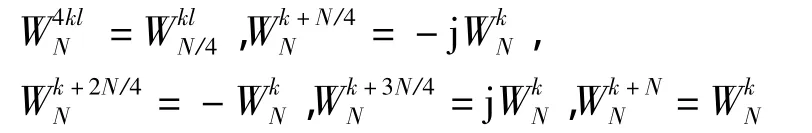
令 a(l)=x(4l)，b(l)=x(4l+1)，c(l)=x(4l+2)，d(l)=x(4l+3)，则序列 X(k)划分为4个长度为N/4的子序列:

图3是DIT基4FFT的蝶形单元运算流程图，DIT基4FFT的每次蝶形单元运算需要3次复数乘法，8次复数加法，转变实数计算即为12次实数乘法和22次实数加法，即需要34次实数乘(加)操作。

图3 DIT基4 FFT的蝶形单元运算流程图Fig．3 Radix-4 DIT FFT butterfly diagram

2．2 FMA优化的FFT蝶形单元运算

2．2．1 FMA优化的DIT基2FFT蝶形单元计算

假定DIT基2FFT的一个蝶形单元的两个输入分别为A和B，输出分别为Y1和Y2，蝶形因子为W，下标r和i分别表示复数的实部和虚部，根据式(1)，则有:

根据式(3)，DIT基2 FFT的蝶形单元运算可以分解成两步完成:

1)计算中间结果ˉA，ˉB:

2)计算输出结果Y1和Y2:

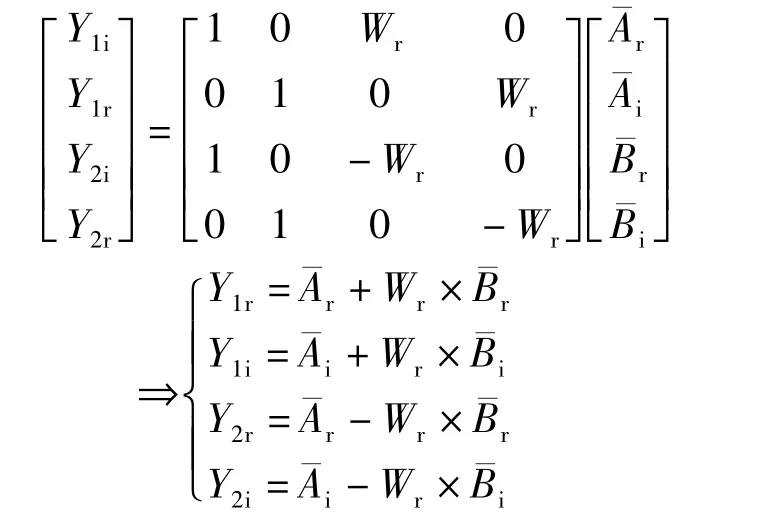
其中，步骤1的计算由2条FMA指令完成，步骤2的计算由4条FMA指令完成。从而计算一个DIT基2 FFT蝶形单元仅需要6条FMA指令操作，相比传统的计算方式减少了4次。在传统的计算方法下，计算N点的DIT基2 FFT需要的浮点操作次数为5N log2N;FMA优化后需要的浮点操作次数减少到3N log2N，减少了40%。

2．2．2 FMA优化的DIT基4FFT蝶形单元计算

假定DIT基4 FFT的一个蝶形单元的4个输入分别为 A，B，C，D，输出分别为 Y1，Y2，Y3，Y4，3个蝶形因子分别为W1，W2，W3，下标r和i分别表示复数的实部和虚部，根据式(2)，则有:

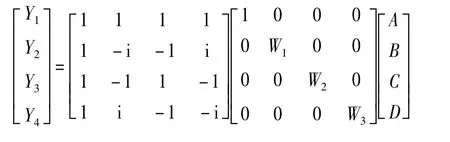
根据式(4)，DIT基4 FFT的蝶形单元运算可以分解成两步完成:

1)计算中间结果ˉA，ˉB，ˉC，ˉD:

其中，步骤1的计算由12条FMA指令完成，步骤2的计算由12条FMA指令完成。从而计算一个DIT基4FFT蝶形单元仅需要24条FMA指令操作，相比传统的计算方式减少了10次。在传统的计算方法下，计算N点的DIT基4 FFT需要的浮点操作次数为8．5N log4N;FMA优化后需要的浮点操作次数减少到6N log4N，减少了29．4%。

2．3 混合基4和基2的FFT计算方法

如图4所示，对于任意的N=2n，可采用混合基4和基2的FFT方法加速FFT的计算。若n是偶数，令n=2m，则N=22m=4m;若n是奇数，令n=2m+1，则 N=22m+1=4m×2。因此，N 点的FFT计算可转化为m级基4FFT或者m级基4FFT和最后一级的基2 FFT计算。

图4 混合基4和基2的FFT计算流程Fig．4 FFT computation diagram ofmixed radix-2/4

2．4 旋转因子向量访问的优化

传统的基4 FFT计算方法中，每个蝶形单元运算需要乘以3个不同的旋转因子:和FMA优化后的蝶形单元运算只需计算2个不同旋转因子:WiN和W2Ni，并且预先计算出旋转因子虚部/实部(Wi/Wr)的值，然后把旋转因子按实部(Wr)、虚部/实部(Wi/Wr)交叉存储放置。这样，能减少旋转因子存储的个数。由于向量处理器只能连续存取向量数据，所以每级FFT运算的不同旋转因子都要单独放置。

同样，DIT基2 FFT算法需要预先计算旋转因子WiN和虚部/实部(Wi/Wr)的值，并且按实部(Wr)、虚部/实部(Wi/Wr)交叉的方式存放。

以1024点的DIT基4 FFT为例，算法由5级蝶形运算实现，且每一级不同旋转因子所需的数目分别为:1个、4个、16个、64个和256个。由此可知，第1级和第2级的不同旋转因子的数目少于VPE的个数，并且第1级需要乘的旋转因子的值为1，所以可以省略。为了提高运算的并行度，可以把第2级所需的旋转因子进行冗余存放4次。

表1 1024点DIT基4 FFT的旋转因子Tab．1 Twiddle factors of 1024-point radix-4 DIT FFT

3 性能测试与分析

在向量处理器Matrix上对不同点数的FFT计算性能进行了测试(称 MatrixFFT)，并与 Intel，AMD，IBM 平台上的 MKL，ACML，ESSL 和 FFTW 3．0算法库的性能进行比较。实验平台中，Matrix的主频为1GHz(双精度峰值性能为96GFLOPS)，MatrixFFT的测试结果为RTL级仿真环境下的测试性能数据;比对实验的 CPU中，Intel选择主频3．0GHz Intel Xeon Core Duo(Woodcrest)(峰值性能为12GFLOPS);AMD选择主频2．2 GHz Dual Core AMD Opteron(峰值性能为4．4GFLOPS);IBM选择主频2GHz PowerPC 970(峰值性能为10GFLOPS)，其性能数据选自FFTW网站报告的评测数据［8］。

图5和图6分别给出了在Matrix上测试的不同点数的基2和基4FFT的单精度和双精度计算性能。从图5、图6中可以看出，在点数较小时，FFT的性能较低，随着点数的增大，FFT的计算性能显著提高，16K点的单精度基2和基4FFT性能分别达到74GFLOPS和98GFLOPS，计算效率分别为38．5%和51．04%。16K点的双精度基2和基4FFT 性能分别达到48．83GFLOPS 和49．05GFLOPS，计算效率分别为50．08%和51．09%。

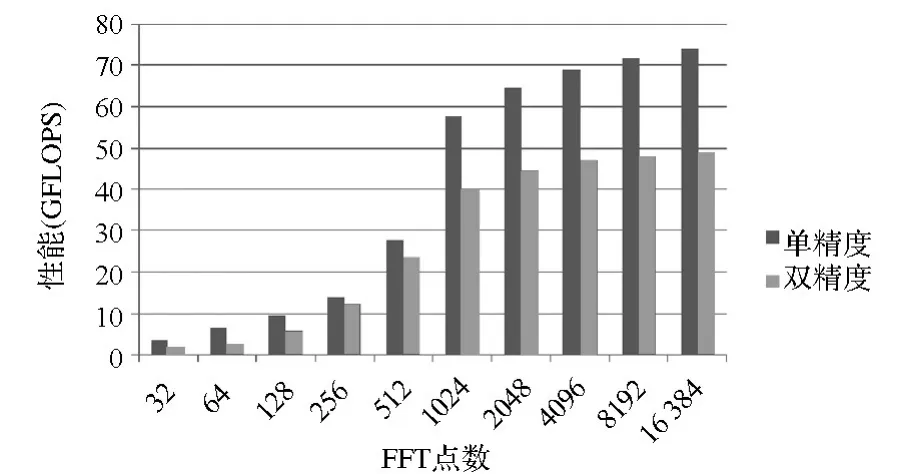
图5 基2FFT的计算性能Fig．5 Performance of radix-2 FFT

图6 基4FFT的计算性能Fig．6 Performance of radix-4 FFT

图7 对比了不同点数的双精度FFT在 FMA优化前后的计算性能，从图7中可以看出，无论是DIT基2FFT，还是 DIT基4FFT，经过 FMA优化后，FFT的计算性能均显著提高，其中 DIT基2FFT的计算性能平均提高30．4%，DIT基4FFT的计算性能平均提高30．3%。

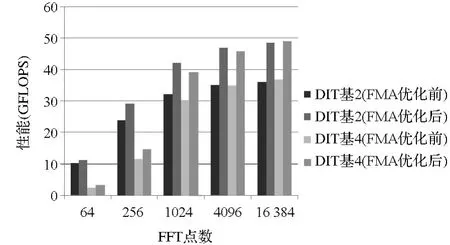
图7 FMA优化的FFT性能对比Fig．7 Performance comparison of FMA optimized FFT

表2 不同处理器平台下FFT性能(MFLOPS)Tab．2 FFT performance of different processors(MFLOPS)

表3 不同处理器平台下FFT计算效率Tab．3 FFT efficiency of different processors

表2和表3分别从计算性能和效率两方面给出了不同点数的双精度FFT分别在Matrix，Intel，AMD，IBM 平 台 上 的 MKL，ACML，ESSL 和FFTW3．0算法库测试结果。

从绝对计算性能上看，MatrixFFT的性能远超其他几种算法库，主要原因是Matrix的峰值性能远超对比CPU的峰值性能;另一方面也体现出提出的基于FMA优化的FFT计算效率较高，能够充分发挥Matrix的计算性能。这一点从表3可以看出，在点数较小时，MatrixFFT的计算效率较低，这是因为Matrix是向量处理器，点数较小时，软件流水中的循环填充和排空的开销在整个计算中的占比较高，影响计算效率。在点数超过1024点以后，MatrixFFT的计算效率显著提高，在4K点以后，计算效率都是最高的，其中16K点效率达50．86%，而对比的其他算法库效率分别是47．88%，36．69%，26．83%，29．27%，12．28%。

4 结论

本文针对 FMA结构的向量处理器，提出FMA加速FFT计算的向量化方法。通过优化和重组FFT算法的蝶形单元运算流程，将原本不平衡的乘法和加法操作组合成融合乘加操作，利用FMA指令减少FFT计算的浮点操作指令次数，进而提高FFT算法的计算性能和向量处理器的计算效率，提高硬件资源的利用率，加速FFT算法的计算性能。

References)

［1］ 刘仲，陈跃跃，陈海燕．支持任意系数长度和数据类型的FIR滤波器向量化方法［J］．电子学报，2013，41(2):346-351．LIU Zhong，CHEN Yueyue，CHEN Haiyan．A vectorization of FIR filter supporting any length and data types of coefficients［J］．Acta Electronica Sinica，2013，41(2):346-351．(in Chinese)

［2］ 刘仲，邢彬朝，陈跃跃．一种面向多核处理器的高效并行PCA-SIFT算法［J］．国防科技大学学报，2012，34(4):103-107．LIU Zhong，XING Binchao，CHEN Yueyue．An efficient parallel PCA-SIFT algorithm for multi-core processor［J］．Journal of National University of Defense Technology，2012，34(4):103-107．(in Chinese)

［3］ Pease M C．An adaptation of the fast Fourier transform for parallel processing［J］．Journal of the ACM，1968，15(2):252-264．

［4］ Linzer EN，Feig E．Implementation ofefficient FFT algorithms on fused multiply-add architectures［J］．IEEE Transactions on Signal Processing，1993，41(1):93-107．

［5］ Goedecker S．Fast radix 2，3，4，and 5 kernels for fast Fourier transformations on computers with overlapping multiply-add instructions［J］．SIAM Journal on Scientific Computing，1997，18(6):1605-1611．

［6］ Karner H，Auer M，Ueberhuber CW．Multiply-add optimized FFT kernels［J］．MathematicalModels and Methods in Applied Sciences，2001，11(1):105-117．

［7］ Voronenko Y，Puschel M．Mechanical derivation of fused multiply-add algorithms for linear transforms［J］． IEEE Transactions on Signal Processing，2007，55(9):4458-4473．

［8］ Frigo M，Johnson S G．BenchFFT［EB/OL］．［2014-03-15］．http://www．fftw．org/benchfft/．

［9］ Lobeiras J，Amor M，Doallo R．Influence of memory access patterns to small-scale FFT performance［J］． Journal of Supercomputing，2013，64(1):120-131．

［10］ Li Y，Zhang Y Q，Liu Y Q，et al．MPFFT:An auto-tuning FFT library for OpenCL GPUs［J］．Journal of Computer Science and Technology，2013，28(1):90-105．

［11］ 何涛，朱岱寅．大点数一维FFT的GPU设计实现［J］．计算机工程与科学，2013，35(11):34-41．HE Tao，ZHU Daiyin．Design and implementation of largepoint1D FFT on GPU［J］．Computer Engineering ＆ Science，2013，35(11):34-41．

［12］ Cooley JW，Turkey JW．An algorithm for the machine calculation of complex Fourier series［J］．Mathematics of Computation，1965，19:297-301．