惯性信息辅助的星像点质心提取方法*

吕汉峰，张 良，王鼎杰，吴 杰

(国防科技大学航天科学与工程学院，湖南长沙 410073)

星敏感器是提供天文导航信息的重要设备。在星敏感器技术中，星像点质心提取是一项基础性的技术，它是星敏感器能提供有效地导航信息的前提，而且质心的提取精度对星敏感器的后续工作如星图识别等影响重大，同时它也在很大程度上决定了星敏感器最终的导航信息精度［1-3］。星敏感器在测量过程中，由于曝光时间、载体角运动及噪声等因素的存在，星体在星敏感器像平面上的成像不再是独立的点而是一片区域，星像点质心提取就是要从这片区域中找到最优的星像点质心位置。

目前的星像点质心提取算法［1-6］研究多以星敏感器的静态成像为前提，不考虑其在曝光过程中可能存在振动等情形，在此假定下这些算法的质心提取精度一般可达到亚像素级。但在星敏感器的实际工作过程中，角振动环境不可避免地存在，如果忽略这些情况则会产生较大的质心提取误差［7］。另外星敏感器通常与惯性设备一起使用，也就是说星敏感器工作过程中的角振动信息可以被惯性设备测量到。如果在提取星像点质心的过程中充分利用这些测量到的角振动信息，则应该可以较大程度地降低振动对星敏感器测量的影响，减小质心提取误差。本文正是基于这一思路提出了惯性信息辅助的星像点质心提取方法。

1 惯性信息辅助像点质心提取模型

1．1 恒星在星敏感器中的成像模型

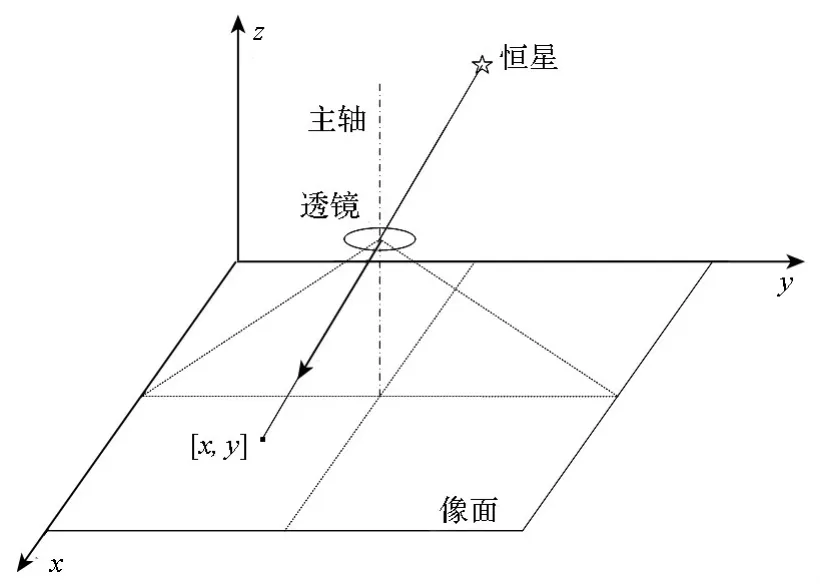
图1 恒星投影模型Fig．1 Star imagingmodel

这里的成像模型由两个部分构成:恒星的点投影模型和投影点的能量分布模型。目前恒星的投影模型均采用小孔成像模型，如图1所示。假定恒星方向矢量在星敏感器体系s中表示为es，星敏感器的视场为γ，像面的像素为N×N，则恒星在像面的投影点坐标可表示为:

式(1)表明，只需知道恒星在星敏感器体系中的单位矢量就可以计算出它在像面上的投影点坐标。

实际成像过程中恒星的投影并不是一个点而是像面上的一片区域。像点质心的提取正是利用这片区域的灰度值进行的，区域中每个像素的灰度值大小就表征了其所接受的恒星的能量大小。常用的能量密度分布模型是以投影点为中心的二维高斯分布函数，如式(2)所示。

式(2)中，［x，y］表示恒星在像面的投影点，I(xi，yi)表示像面上［xi，yi］处的能量密度，σ 表示能量密度集中指数。图2是单维的能量密度分布示意图。

图2 单维能量密度分布示意图Fig．2 Sketch map of power density distribution

则可知第k个像素区域Ωk的能量密度Pk为:

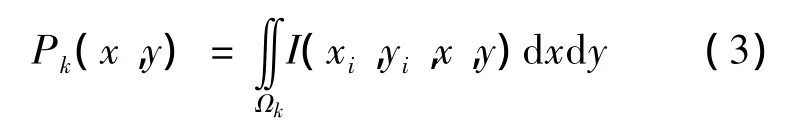
假定曝光时间为Δt且在整个曝光时间内像素区域接受的能量未饱和，则第k个像素的灰度值Gk与其能量密度之间的线性关系可表示为:

其中，c为能量与灰度值之间的转换常数。式(4)表明第k个像素的灰度值与恒星在像面的投影点［x，y］有关。

1．2 惯性信息辅助模型

假定星敏感器体系相对于载体系b的固联安装矩阵为Csb，星敏感器体系相对于惯性系的角速度为ωis，载体系相对于惯性系的角速度为ωib，则易知对于τ1和τ2时刻，假定它们的间隔δτ较小，则这两个时刻的星敏感器体系相对于惯性系的姿态矩阵Csi有如下关系:

式(5)中，［(·)×］表示由矢量(·)生成的叉乘矩阵。

假定恒星在惯性系中的方向矢量为ei，则τ1和τ2时刻该恒星在星敏感器体系中的单位矢量可表示为:

式(5)和式(6)结合可得:

假定在δτ时间内惯性设备对载体角增量的敏感度为αb，则式(7)可改写为

结合式(1)和式(8)可知，若τ1时刻恒星在像面的投影点已知，则根据惯性设备在δτ时间内的测量信息可以计算出τ2时刻该恒星在像面的投影点。

1．3 星像点质心提取算法

若星敏感器在曝光过程中载体存在振动，则恒星的投影点在像面上就呈现出一条轨迹。若惯性设备可以测得振动信息，则这条轨迹就可知。

若已知曝光初始时刻的恒星投影点，则根据式(1)、式(8)和曝光时间内的角增量即可计算出投影点的轨迹，然后利用式(2)、式(3)和式(4)即可计算出曝光后恒星投影区域内各像素的灰度值，则易知这些灰度值都是初始投影点［x，y］的函数，记为)。

另外，曝光后通过图像处理的方法得到的投影区域内各像素的灰度值记为。根据能量守恒则式(10)成立。

其中，N为投影区域所包含像素的个数。

如果初始投影点选择合适，则必然有式(11)成立。

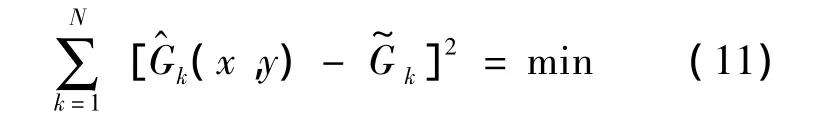
若记:

则由式(11)可知:

由式(12)即可计算出初始投影点的坐标。但由式(1)和式(2)可知式(12)是较强的非线性函数，因此通常采用线性化的方式进行计算，而初始投影点的初值可选为投影区域的灰度加权中心。

由式(12)计算的初始投影点理论上讲是最优的，但这个过程中需要计算复杂的偏导函数及线性化，计算量比较大。从另外一个角度看，如果式(11)成立，则由计算的灰度加权中心应该和计算的相同。如果不同，则两个中心的差异可认为是初始投影点不准确所致。利用这个差异对初始投影点进行补偿，然后重新计算和灰度加权中心，如此重复直至两个中心重合。这个过程相对来讲计算量比较小，并且应该也可以得到较准确的初始投影点。在得到初始投影点之后便可计算得到曝光结束时刻的恒星像点质心。

综上分析，惯性信息辅助的星像点质心提取算法的框图大致如图3所示。

2 仿真验证

为比较本文提出的惯性信息辅助算法与传统算法在振动环境下的星像点质心提取精度及本文算法的适用性，现进行仿真试验。仿真试验主要分成两部分，第一部分用来比较本文算法与传统算法的质心提取精度;第二部分用来分析算法的适用性，即相关因素对本文算法质心提取精度的影响。

图3 惯性信息辅助星像点质心提取算法流程图Fig．3 Flow chart of the star spot centroidingmethod with inertialmeasurement information

2．1 仿真条件

仿真过程中采用Tycho2星表，设置星敏感器视场为8°×8°，像素为512×512，能量密度集中指数为0．45像素，曝光时间为25ms，惯性设备的零漂为0．1°/h，角增量输出频率为200Hz，并假定振动角速率最大值不超过3°/s。为便于计算假定星敏感器体系与载体系重合。在全天球范围内随机产生1000组姿态作为星敏感器曝光时刻的姿态，然后在曝光过程中产生振动。利用星像点质心提取算法处理曝光得到的图像并统计相关算法的星像点质心提取精度。采用文献［1］中的算法作为参考，在静态条件下该算法的提取精度优于0．1像素。图4是某次振动条件下星敏感器曝光后得到的图像。

图4 振动条件下星敏感器曝光后的图像Fig．4 Camera image after the exposure of star sensor in vibration environment

2．2 算法提取精度比较

利用本文算法和传统算法处理图4得到星像点质心如图5所示，各质心坐标如表1所示。

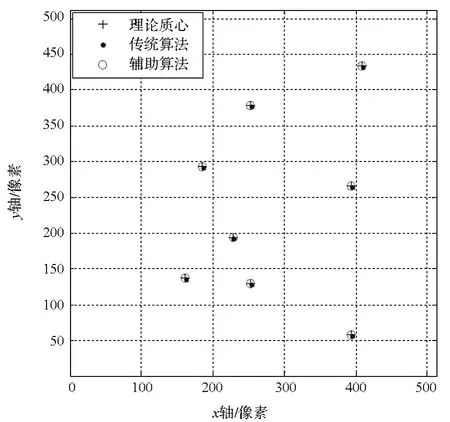
图5 两种算法提取的星像点质心比较Fig．5 Comparison of the centroids of the twomethods

由图5可知，传统算法计算得到的各星像点质心偏离理论质心较远，而利用惯性信息辅助的算法得到的质心则比较靠近理论质心。表1中的数据更直观地表明了这一结果。表1中的算法误差是指算法得到的质心至理论质心的距离。由表1可知，针对图4所示的情况，传统算法得到的质心偏离理论质心1．7像素左右，而辅助算法得到的质心误差则在0．1像素以下。

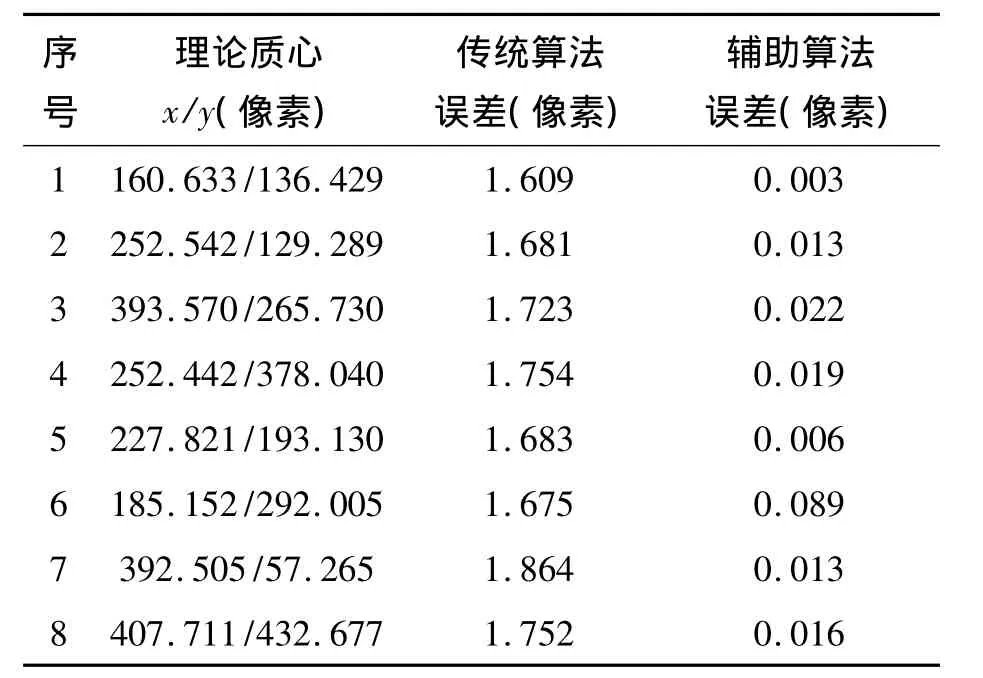
表1 各星像点质心及算法误差Tab．1 Theoretical centroids and errors

通过对1000幅振动条件下星敏感器曝光图像的处理，经过统计得到，在振动角速率小于3°/s的情况下，传统算法的提取精度为0．691像素，辅助算法的提取精度为0．011像素。这充分表明了惯性信息辅助星像点质心提取算法在振动条件下依然可以获得亚像素级的质心精度。另外这种辅助算法的计算量比传统算法略大，但计算耗费的时间也同样可以忽略不计。

2.3 算法适用性分析

由式(2)和式(8)可知，影响本文算法质心提取精度的主要因素有能量密度分布模型的准确性和角增量的测量精度，这两者主要取决于能量密度集中指数σ和惯性设备的零漂。在仿真过程中设置能量密度集中指数σ的变化范围为0．1～1．5 像素，零漂的变化范围为 0．01 ～10°/h，它们对辅助算法提取精度的影响如图6和图7所示。由图6可知随着能量密度集中指数σ的增大，辅助算法的质心提取精度逐步提升至0．01像素左右。而且在整个变化过程中，质心提取精度基本都在亚像素级。由图7可知随着零漂的增大，辅助算法的质心提取精度稍微变差，但仍然在0．01像素左右。

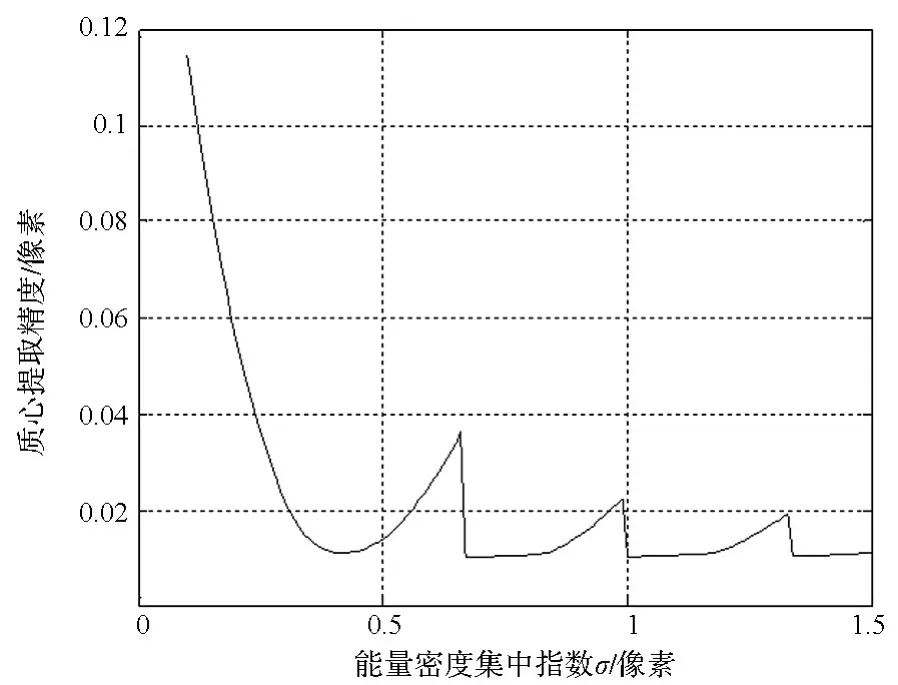
图6 σ对辅助算法质心提取精度的影响Fig．6 Effect ofσ on the centroid precision

图7 零漂对辅助算法质心提取精度的影响Fig．7 Effect of the drift on the centroid precision

以上仿真分析表明，本文提出的惯性信息辅助星像点质心提取算法在振动条件下依然可以有效准确地提取出各星像点的质心。

3 结论

本文研究了振动条件下恒星在星敏感器中的成像过程，提出了惯性信息辅助的星像点质心提取模型，并建立了惯性辅助质心提取算法。仿真结果表明:当振动角速率小于3°/s时，辅助算法的质心提取精度在0．01像素左右，而且星敏感器的能量密度分布模型的准确性和惯性设备的角增量测量精度在一定范围内对提取精度的影响较小。

References)

［1］ 张广军．星图识别［M］．北京:国防工业出版社，2011．ZHANG Guangjun．Star identification［M］．Beijing:National Defense Industry Press，2011．(in Chinese)

［2］ 吴峰．自主导航星敏感器关键技术的研究［D］．苏州:苏州大学，2012．WU Feng．Study on the key technologies for autonomous star sensors［D］．Suzhou:Soochow University，2012．(in Chinese)

［3］ 贾辉．高精度星敏感器星点提取与星图识别研究［D］．长沙:国防科学技术大学，2010．JIA Hui．Star centroid estimation and star identification of high accuracy star tracker［D］．Changsha:National University of Defense Technology，2010．(in Chinese)

［4］ Quine B M，Tarasyuk V，Mebrahtu H，et al．Determining star-image location:a new sub-pixel interpolation technique to process image centroids［J］．Computer Physics Communications，2007，177(9):700-706．

［5］ 魏新国，张广军，江洁．星敏感器中星图图像的星体细分定位方法研究［J］．北京航空航天大学学报，2003，29(9):812-816．WEI Xinguo，ZHANG Guangjun，JIANG Jie．Sub divided locating method of star image for star sensor［J］．Journal of Beijing University of Aeronautics and Astronautics，2003，29(9):812-815．(in Chinese)

［6］ Shortis M R，Clarke T A，Short T A．Comparison of some techniques for the subpixel location of discrete target images［C］//Proceedings of Photonics for the Industrial Applications．International Society for Optics and Photonics，1994，2350:239-250．

［7］ 季家兴，王新龙．载体运动对星敏感器星点光斑定位的影响分析［J］．青岛科技大学学报(自然科学版)，2010，31(2):194-200．JIJiaxing，WANG Xinlong．Effects of carriermovement on the star location of star sensors［J］．Journal of Qingdao University of Science and Technology(Natural Science Edition)，2010，31(2):194-200．(in Chinese)