基于FPGA的小时间尺度仿真系统的静止同步无功补偿仿真研究

穆清，张星，王祥旭，孙倩

(中国电力科学研究院，北京市100192)

0 引言

现代电力系统中，静止同步无功补偿器已经成为重要的柔性交流输电设备，可以在交流系统故障等扰动情况下提供更理想的电压支撑。目前，静止同步无功补偿器已替代基于晶闸管设备的无功补偿设备，如静止无功补偿器(static var compensator，SVC)等，成为电力系统规划和设计的首选。

随着静止同步无功补偿器的发展，其分析和仿真的需求也在增加。静止同步无功补偿器仿真需要采用小步长仿真确保精度;离线仿真工具例如PSCAD/EMTDC，可以使用小时间步长(1～2 μs)。然而，实现更小的时间步长会产生较长的计算时间，成为实时仿真的巨大挑战［1］。

现阶段实时数字仿真系统大都采用并行处理的硬件系统和高速数字处理芯片(digital signal processor，DSP)，利用数学上可分割子系统在各个运算芯片或芯片组间分配计算任务，继承了数字仿真软件和模拟仿真器的优点:经济、快捷、参数调整方便、体积小、建设周期短、功能强大，对于测试的系统可实时闭环运行，这是物理仿真系统所无法比拟的。

然而在电力系统全数字实时仿真系统中，各并行处理器间的通信、数据交换及模型算法等各方面因素限制了仿真规模的提升。目前，RT-LAB在其服务器平台上只能提供20 Sμs步长的静止同步无功补偿器的仿真。小时间尺度仿真的主要限制在于中央处理器(core processor unit，CPU)和操作系统开销，这将在每个小时间步长中占很大一部分时间。RTDS可以提供静止同步无功补偿器小时间尺度仿真，但由特殊的硬件电路(DSP)提供支持，规模受到硬件限制［2］。

因此，通用处理器和DSP已经不能满足小时间尺度的实时仿真需求，针对新型电力电子设备的高速开关特征，基于场效应可编程逻辑阵列(field programmable gate array，FPGA)的实时仿真技术应运而生。

FPGA是由客户定制设计的可配置集成电路。传统FPGA容量小，无法承担仿真计算的复杂逻辑功能。当代FPGA具有大量的逻辑门和内存(randomaccess memory，RAM)块的资源来实现复杂的数字运算［3-4］。例如，Xilinx的 Virtex-7系列，其提供的资源和性能提升了好几倍。这个发展促进了FPGA实现更大规模和更高精度的仿真。

现有基于FPGA的仿真器主要应用于硬件测试和系统［5-6］。因为资源的限制，这一代FPGA不能支持双精度浮点运算，在准确度要求较高的大规模仿真领域受到了限制［7］。

本文探索基于新一代FPGA的静止同步无功补偿器的仿真建模，通过案例分析说明静止同步无功补偿器的故障特性和正确性验证。

1 适用于实时仿真的静止同步无功补偿模型

静止同步无功补偿器的模型各不相同。基本的数学函数模型应用广泛，由于其固定的拓扑结构，并不灵活。本文研究基于分立元件的小时间尺度仿真器的仿真建模。

此外，静止同步无功补偿器的实际拓扑结构分为两电平、三电平和链式。本文讨论两电平的模型，其他拓扑结构的建模与两电平相似。

1.1 电路拓扑

静止同步无功补偿器的模型如图1所示，静止同步无功补偿器在交流侧包括3个组成部分，1个含内阻的交流电压源、1个变压器和1个LC谐振滤波器。

两电平换流器可以简单的验证FPGA进行小时间尺度仿真的可行性，因此作为本文研究的重点。换流器通过分立电路进行建模，包括绝缘栅双极晶体管(insulated-gate bipolar transistor，IGBT)、二极管、缓冲电路(串联电容器和电阻分支)以及电压和电流测量。2个大直流电容器接地，平衡两极的直流电压。

图1 静止同步无功补偿器电路结构Fig.1 Circuits Topology of STATCOM

1.2 控制器模型

静止同步无功补偿器的控制器模型如图2所示，该控制器是典型的双闭环控制方案。内环包括带上限和下限有功电流调节和无功电流调节，比例积分(proportion integration，PI)调节器的参数合理整定，以获得快速响应跟踪。外环有2个调节器，产生内环无功功率调节器的参考和内环有功功率调节器的参考。这2个调节器可以在不同的模式中选择不同的控制目标。有功功率调节始终控制电容器C1和C2上的电压，无功功率调节可以在无功控制和交流电压控制之间自由和迅速地切换。

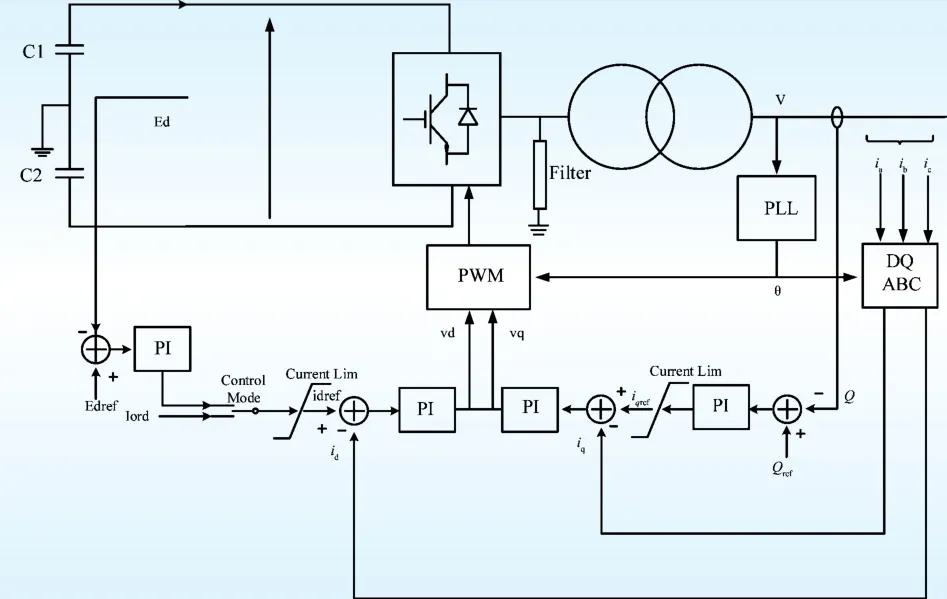
图2 静止同步无功补偿器的控制策略Fig.2 Control strategy of STATCOM

2 小时间尺度实时仿真关键算法研究

基于电容电感的等值开关(L/C)技术又名相应离散化电路等值(associated discrete circuit equivalent circuit，ADC)模型。当开关处于导通状态时，用电感支路L模拟;当开关处于关断状态时，用电容和电阻的串联支路模拟。由于开关投切过程中产生了状态突变，所以在电容支路中引入电阻元件，提供对电路的阻尼，改善系统的稳定性，其等值电路图如图3所示。

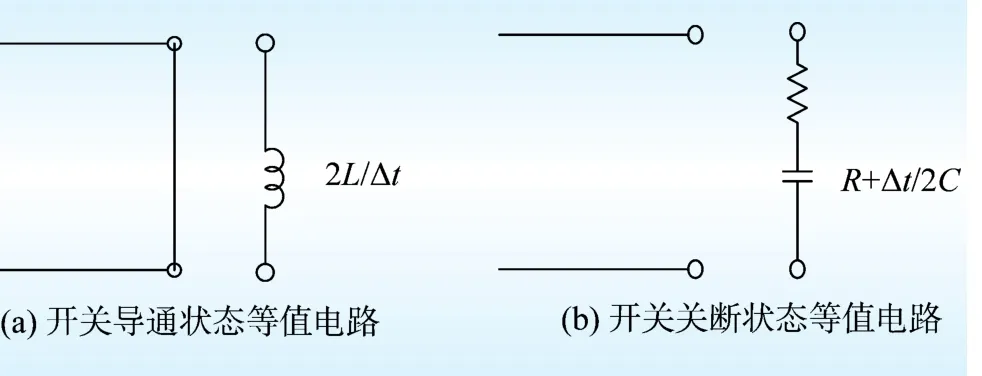
图3 开关小步长仿真模型Fig.3 Small time-step switch model

由图3可知，ADC开关导通和关断的等值电阻是1个与电感L，电容C和仿真步长ΔT相关的函数，可以通过设定合理的等效L和C的值使得ADC开关导通和关断时的等值电阻Z不变，这样开关所在电网络的导纳矩阵保持不变，在开关动作时刻不需要重新生成网络矩阵并求解，仿真效率大大提高。此时，开关导通和关断状态的不同完全由开关元件的历史电流源的差别体现。

为了使开关状态改变时开关的等值支路导纳不变，开关导通和关断状态的等值电阻必须相等，以隐式积分法为例，遵循式(1):

目前电磁暂态程序广泛使用的隐式梯形积分法虽然在稳定性和准确性上有一定的优势，但是处理开关时，无法抑制系统的数值振荡。后退积分法由于在稳定性上比隐式梯形积分更加出色(常见的后退积分法包括一阶的后退欧拉和高阶的Gear积分法)，在电路拓扑频繁变化的场合，推荐使用后退积分法。由于基于ADC开关的小步长仿真模型主要解决大量电力电子器件的刚性电路，不同的离散化方法对仿真结果有很大的影响，需要选择合适的积分方法。表1说明了在不同数值积分方法下的等值支路导纳和等值电流源的具体表达式。其中，Y表示离散元件的等值电抗，un表示元件两端电压，in表示流经元件电流。

表1 离散小步长开关模型Table 1 Discrete small time-step switch model

3 实时仿真系统结构设计

基于FPGA的小步长仿真系统采用了双精度浮点计算，缓解了截断误差，对大规模长时间的仿真造成的累计误差和收敛性都有较大的改善。同时，由于系统采用了与CPU仿真一致的双精度浮点计算，可以提供与离线仿真完全一致的仿真结果，提高了仿真的正确性。小时间尺度仿真系统的功能如图4所示。

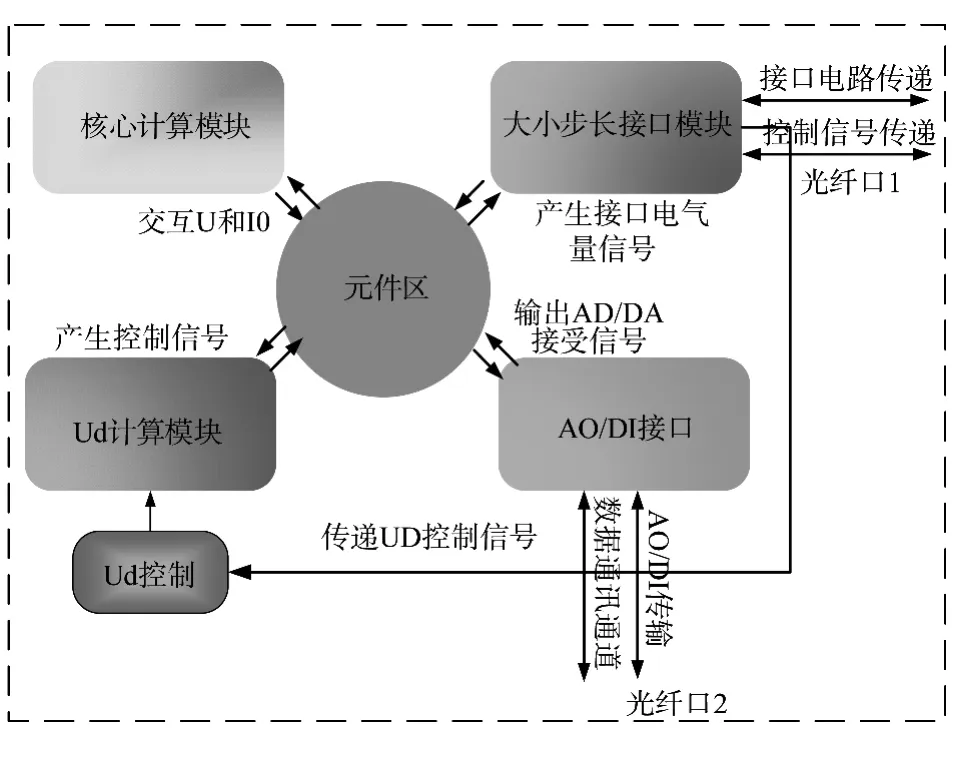
图4 小时间尺度仿真系统结构Fig.4 Structure of small time-step simulator

3.1 核心计算模块

在FPGA上运行的小时间尺度仿真系统是1个小规模的完整的电磁暂态仿真系统，其核心是求解1个线性方程组，并在核心计算模块中完成。

65

核心计算模块的基本工作是实时高效的计算矩阵和向量乘积x=GAC－1y，其中GAC－1矩阵于仿真开始的初始化阶段就由服务器端计算完成，并写入FPGA的相关存储单元中。

此计算的核心是并行实现矩阵(GAC－1)与向量(y)的乘法，本系统采用了乘累加结构，如图5所示。

乘累加结构是基于底层基本处理单元(processing element，PE)的循环乘累加器结构。其不但有效改善了核心计算模块整体处理延迟，而且其处理延迟与矩阵维数线性相关的特性，使其对低维数矩阵体现出较短的处理时间，更强的灵活性。

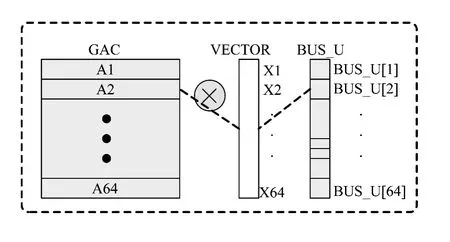
图5 矩阵乘法计算模块Fig.5 Matrix multiplication calculation module

3.2 元件区

元件区为仿真程序中的物理元件描述部分，存储仿真中的元件模型的相关变量和结果，完成一些简单的元件变量的更新。元件区包括:单相串联RLC元件(SLA)、三相串联RLC元件(LA)、单相变压器元件(STB)、三相变压器元件(TB)、时控开关(BRK-1)、晶闸管原件(BRK-5)、GTO 原件(BRK-6)、IGBT开关对(BRK-8)、单相可控电压源(CVS)、单相可控电流源(CIS)、单相普通电压源(SCV)、单相普通电流源(SCI)、三相普通电压源(CV)、三相普通电流源(CI)、分布参数网络解耦元件(LC)。

3.3 大小步长接口模块

小时间尺度仿真模拟的是电力系统中的一部分含有电力电子设备的网络模型，由于仿真精度的要求而采用小步长;电力系统中其余电网模型采用大步长(典型为 50 μs)仿真，在现有基于高性能机群的ADPSS仿真系统上进行仿真。

小步长仿真和大步长仿真共同模拟一个完整的电力系统，通过特定的仿真算法进行解耦和并行计算，因此大小步长仿真之间需要数据交换和精确同步。小步长仿真通过接口从大步长仿真获取需要的信号，并把大步长仿真需要的信号输出。

为满足通信速率的要求，小步长仿真系统通过光纤通讯与大步长系统交互数据、与外部实际控制装置交互信息。

3.4 用户自定义计算模块

用户自定义(user define interface，UD)是一个用户自定义的模型，包括UD控制模块和UD计算模块。由于大小步长接口模型会接收一些从大步长系统传递而来的控制信号，这些控制信号必须经过处理以后输入到UD计算模块，所以增加1个UD控制模块作为缓存媒介。UD计算模块实现用户自定义的计算，此模块是独立于网络计算模块之外的，包括了四则运算、逻辑运算等模块，计算结果传输给元件区，改变某些特定元件的响应特性。

UD的输入信息通道有2个:从大小步长接口模型交互信息的通道;从DI接口输入的外界控制信息(实际的物理控制设备)的通道。具体来说，UD搭建的模型的参数可能从大步长系统传递而来，因此大小步长接口模型应包含UD控制信息。另外，外界控制系统的输入信号(DI)用来控制部分开关元件。

3.5 AO/DI接口

小时间尺度仿真过程中，可以通过AO/DI接口与外部实际控制装置构成闭环。AO/DI接口主要负责模拟信号输出和开关信号输入，把元件区内的元件状态通过AO通道输出，并从外部获取开关信号以更改元件状态。

DI输入接口模块主要负责外部实际控制装置开关量的输入，要求每块FPGA仿真板卡应具备有36路DI接口，所有通道均采用高速光隔后传输给FPGA的I/O端口。

DI信号的高电平为5 V，低电平为0 V，因此需要进行电压转换而传给FPGA。信号输入通过光电隔离，隔离电压大于500 V DC，输入延迟小于10 ns。要求FPGA能捕捉到开关量信号的跳变时刻，并为其打上相对于仿真步长的时标，时标精度应优于10 ns。仿真程序可根据信号跳变时刻来提高仿真精度。

3.6 控制闭环通讯接口

小时间尺度仿真过程中，亦可通过光纤通讯接口与外部实际控制装置构成闭环，采用通讯方式交互信息。通过设计一种I/O子板来采集外部控制装置的控制信号，然后通过光纤接口与小时间尺度仿真平台进行通信，同样，小时间尺度仿真平台输出的控制信号传递给I/O子板，I/O子板通过数模转换控制外部装置。

4 实时仿真系统试验研究

本文在FPGA仿真系统上进行静止同步无功补偿器的细致测试。首先，具有的FPGA仿真器和一个可行的电磁仿真工具PSCAD之间的结果比较，这可以验证FPGA仿真的正确性。然后，本文将利用这个平台，对静止同步无功补偿器的模型进行各种测试。测试将覆盖所有的运行条件，包括稳定状态和扰动。

4.1 静止同步无功补偿器的试验系统

静止同步无功补偿器的实时仿真试验采用了图1的拓扑结构和图2的控制系统。详细的电路参数见表2。

表2 小步长子网参数Table 2 Subsystem parameters with small time-step

4.2 稳态精确性仿真验证

测试过程中不仅通过示波器对电路信号进行采样，如电压和电流，而仿真的结果将被存储在FPGA存储器上的，可以稍后读取。示波器上的结果显示于图6。

图6 交流系统的电压和静止同步无功补偿器的输出Fig.6 AC voltage and STATCOM output voltage

图6 代表交流系统输出电压和变流器在静止同步无功补偿器的输出电压。本文同时提取了换流器出口电压波形，并与PSCAD比较，见图7。

(ADPSS)换流器出口A，B，C三相电压波形比较如图7所示，浅色线代表了仿真器的输出，深色线代表了PSCAD的输出。深色线与浅色线完全重合。这种比较显示了仿真器输出的正确性。

4.3 故障中的响应

这部分显示了静止同步无功补偿器的扰动响应。8 s时刻发生静止同步无功补偿器的出口A相接地故障，并持续0.1 s。如图8，静止同步无功补偿器的交流系统母线A相电压输出大大下降。由于静止同步无功补偿器支撑，出口电压下降幅度减小。在静止同步无功补偿器的直流侧的直流电压略微上升，当干扰被清除快速返回到正常运行状态。如图8，从静止同步无功补偿器产生的注入到交流系统的电流增加。

图7 PSCAD和FPGA比较Fig.7 Comparison between PSCAD and FPGA

5 结语

本文研究了如何基于FPGA的小时间尺度仿真器在小时间尺度下模拟静止同步无功补偿器，提出了基于分立元件的静止同步无功补偿器的建模，并对主要的拓扑结构进行了讨论，按照FPGA的要求仔细对转换器和其他原件建模。

此外，建立了在基于FPGA的小时间尺度仿真平台上的控制系统，包括双回路控制和模式选择。这种控制方案可以在许多应用中提供快速稳定的控制能力。

这些结果表明，静止同步无功补偿器在小时间尺度仿真器上可以得到各种干扰的合理响应。

本文也阐述了基于FPGA的小时间尺度仿真平台的结构和基本仿真算法。此外，仿真器可通过FPGA扩展卡增强其仿真能力，表明该FPGA仿真器可满足各种测试条件和要求。因此，这种建模和仿真可以应用在更多的领域。

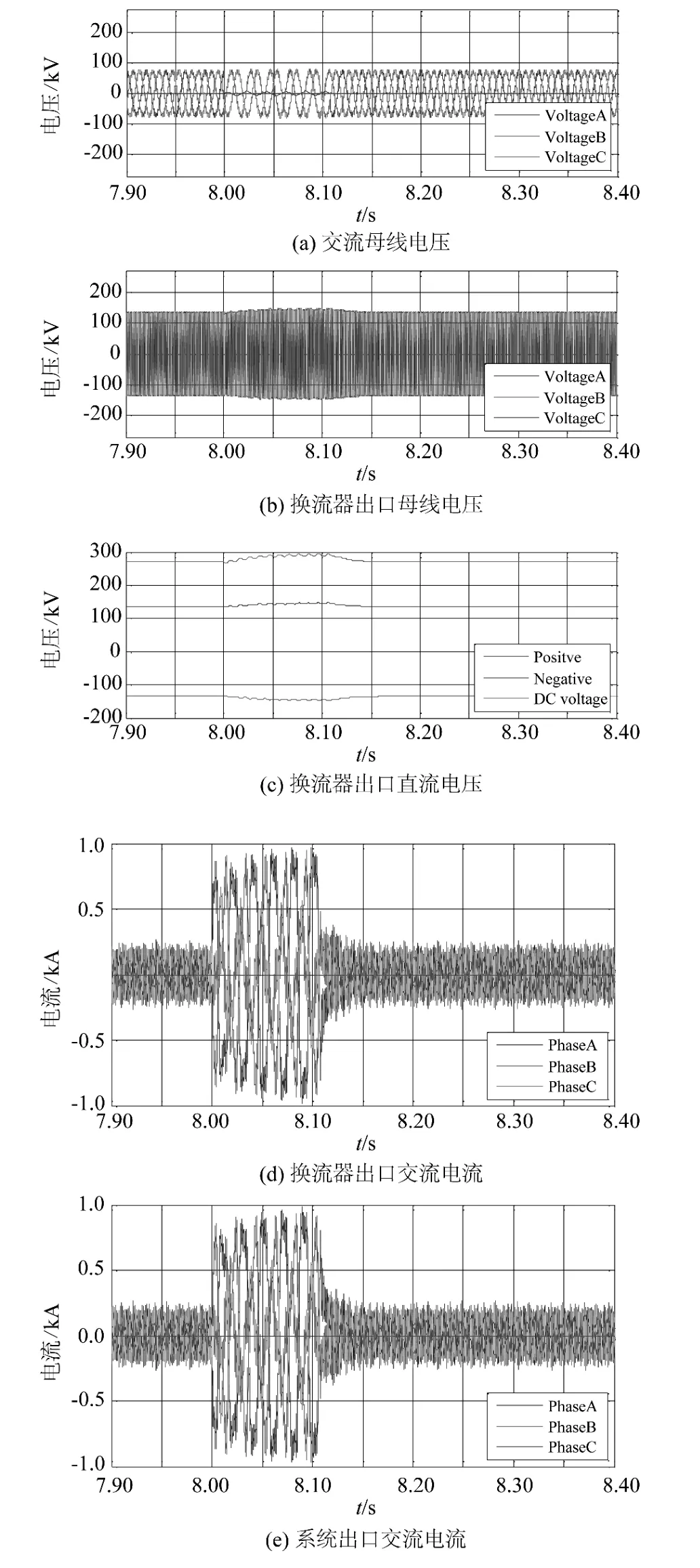
图8 交流扰动的电压电流Fig.8 Voltage and current during AC disturbance

［1］ Bachir T O，Dufour C，Bélanger J，et al．A fully automated reconfigurable calculation engine dedicated to the real-time simulation of high switching frequency power electronic circuits［J］．Mathematics＆Computers in Simulation，2013，91(3):167-177．

［2］Set R M．RTDS Technologies［M］．Inc Manitoba Canada，REV，2006:2001-2002．

［3］ Meka R，Sloderbeck M，Faruque M O，et al．FPGA model of a high-frequency power electronic converter in an RTDS power system co-simulation［C］ //ElectricShip TechnologiesSymposium(ESTS)，IEEE，2013:71-75．

［4］ Luciía O，Urriza I，Barragán L A，et al．Real-time fpga-based hardware-in-the-loop simulation test bench applied to multiple-output power converters［J］．IEEE Transactions on Industry Applications，2011，47(2):853-860．

［5］Myaing A，Dinavahi V．FPGa-based real-time emulation of power electronic systems with detailed representation of device characteristics［J］． IEEE Transactions on Industrial Electronics，2011，58(1):358-368．

［6］Matar M．An FPGA-based real-time digital simulator for power electronic systems［D］．University of Toronto，2009．

［7］ Zhang X，Gong C．Dual-buck half-bridge voltage balancer［J］．IEEE Transactions onIndustrialElectronics， 2013， 60(8):3157-3164．

［8］Yuan C，Dinavahi V．FPGA-based real-time EMTP［J］．IEEE Transactions on Power Delivery，2009，24(2):892-902．

［9］王成山，丁承第，李鹏，等．基于FPGA的配电网暂态实时仿真研究(一):功能模块实现［J］．中国电机工程学报，2014，34(1):161-167．Wang Chengshan， DingDicheng， Li Peng， et al． Real-time transient simulation for distribution systems based on FPGA．Part I:Module realization［J］．Proceedings of the CSEE，2014，34(1):161-167．

［10］王成山，丁承第，李鹏，等．基于FPGA的配电网暂态实时仿真研究(二):系统架构与算例验证［J］．中国电机工程学报，2014，34(4):628-634．Wang Chengshan， Ding Dicheng， Li Peng， et al． Real-time transient simulation for distribution systems based on FPGA．Part II:System architecture and algorithm verification［J］．Proceedings of the CSEE，2014，34(4):628-634

［11］Jiadai L，Dinavahi V．A real-time nonlinear hysteretic power transformer transient model on FPGA［J］．IEEE Transactions on Industrial Electronics，2014，61(7):3587-3597．

［12］ Herrera L，Wang J．FPGA based detailed real-time simulation of power converters and electric machines for EV HIL applications［C］//Energy Conversion Congress and Exposition(ECCE)．IEEE，2013:1759-1764．

［13］Arias-Garcia J，Braga A，Llanos C H，et al．FPGA HIL simulation of a linear system block for strongly coupled system applications［C］// 2013 IEEE International Conference on Industrial Technology(ICIT)，IEEE．2013:1017-1022．

［14］Myaing A，Faruque M O，Dinavahi V，et al．Comparison of insulated gate bipolar transistor models for FPGA-based realtimesimulation of electric drives and application guideline［J］．Iet Power Electronics，2012，5(3):293-303．

［15］Blanchette H F， Ould-BachirT， David JP． A State-space modeling approach for the FPGA-based real-time simulation of high switching frequency power converters［J］．IEEE Transactions on Industrial Electronics，2012，59(12):4555-4567．