大规模电网电磁暂态快速仿真方法

姚蜀军，韩民晓，汪燕，万磊

(1．华北电力大学，北京市102206;2．中国电力科学研究院，北京市100192)

0 引言

机电暂态仿真系统是分析电力系统稳定的重要工具。随着与直流输电(high voltage direct current，HVDC)、柔性交流输电(flexible AC transmission systems，FACTS)、大规模新能源发电等相关的电力电子装置和其他非线性元件广泛应用于电力系统，这些元件引起的波形畸变及其快速暂态过程对系统机电暂态过程的影响越来越大，机电暂态仿真已不能满足电力系统的仿真需求。与机电暂态仿真不同，基于详细建模和小步长的电磁暂态仿真在精确的电路层面上对系统元件进行建模、分析，并计算得到各种暂态响应的时域波形，可以体现系统的电磁暂态行为［1-3］。然而，电磁暂态过程的变化很快，仿真步长一般选取μs级(50～100 μs)。由于所选取的步长小，占据的内存大，计算速度很慢，这使电磁暂态仿真程序的仿真规模受到了限制。为此，人们尝试多种方法来提高电磁暂态的仿真速度，扩大计算规模，这些方法可以分为以下几类。

(1)实时仿真。针对应用类型的不同，电磁暂态仿真可分为离线仿真和实时仿真。对于实时仿真，除了软件技术外，还需要相关硬件装置的配合。然而，考虑到经济性和硬件条件的限制，目前实时仿真器不能完全取代离线的仿真工具，并且仿真规模较小。

(2)改进模型。文献［4-7］基于信号调制理论，提出了动态相量方法。该方法在信号的1个周期内，得到信号的傅立叶系数，并基于不同频次的傅立叶系数，通过Hilbert变换构建不同频次的动态相量。此时的方程包含代数和微分2部分，可以体现系统的动态行为。然而，动态相量法需要进行傅立叶分解，使其本质上不能用于瞬时信号，而是对信号的一种动态平均处理。特别是在信号非线性的情况下，无法进行傅立叶分解，其精度难以保证。例如，对于传统晶闸管型的HVDC，当不考虑换相失败时，基于动态相量的模型比较准确，而当出现换相失败时，由于此时阀电流的无规律性，无法进行动态相量的准确建模，因此，其换相失败时的仿真精度很差。此外，对于基于IGBT的全控器件装置，由于开关频率很高，谐波次数也很高，需要同时建立与高次谐波对应的动态相量方程，因而会极大增加求解的方程数，同时由于高次谐波的频率很高，并不能有效减小仿真步长，因此，也不能有效减少仿真时间。文献［8-11］提出了一种频率偏移(shifted frequency analysis，SFA)的思想，通过对电力系统信号的频率进行偏移处理，将快变化变成慢变化，从而增大仿真步长，但文中并没有给出算例验证。

(3)混合仿真。利用电磁暂态和机电暂态的各自特点，文献［11-17］提出了混合仿真［11-17］。但是，由于电磁暂态仿真采用三相瞬时值的电磁暂态模型，暂态过程中，包含大量谐波成分，而机电暂态仿真采用基波有效值的机电暂态模型，机电暂态部分无法对电磁暂态部分的不同频率进行响应。为此，基于Prony方法等效和频率相关网络等值(frequency dependent network equivalent，FDNE)的电磁 － 机电暂态解耦混合仿真模型被提出。这类方法，通过辨识，得到交流网的频率响应等值模型，将其接入电磁暂态部分。然而，由于这类方法无法处理非线性元件，且系统规模越大，辨识越困难。

(4)并行与多速率。文献［18-29］针对电磁暂态的快过程和机电暂态的慢过程，提出多速率的思想，对于需要详细仿真的采用小步长，对于不需要详细仿真的采用大步长。这些文献中对于大步长采取什么方法没有提及，而不同的大步长方法会极大影响仿真的精度、小步长和大步长间的接口方法和设计。

此外，并行也是一种提高计算速度的思路，目前，基于GPU的并行仿真，是最新的研究趋势［15-19］。但是，由于GPU只能进行细粒度的简单计算，特别是不能很好地处理稀疏矩阵或向量的计算，当没有一个高效的稀疏矩阵求解方法出现之前，还看不到其良好的应用前景。

本文提出一种电磁暂态的快速仿真方法。与SFA构造方法不同，本方法是基于坐标系旋转变换的思想进行推导的，通过旋转变换降低信号的频率，可以根据需要，灵活调节仿真步长，从而加快仿真速度。实际上，基于该方法还可以实现一种多速率的混合方法，对含有电力电子装置或人为设定的部分采用小步长电磁暂态仿真，对于不需详细了解的交流网部分采用本文的大步长电磁暂态仿真。小步长和大步长间按一定的原则接口，可以方便地实现并行计算。本文只给出大步长快速仿真的原理及仿真验证，多速率混合仿真的方法将在后续文章中给出。

1 大步长电磁暂态仿真方法的提出

电力系统时域数字仿真可以看作是对电力系统信号的采样。根据Shannon采样定理，采样频率应该至少是原始信号频率的2倍才能保证采样不丢失原始信号的信息。电磁暂态数字仿真中，根据精度要求，与仿真步长对应的采样频率一般为原始信号的10倍［30］。显然，如果能够显著降低原始信号的频率，那么采样频率也会相应减小，从而可以增大对应的仿真步长，加快仿真速度。

式(1)是常用的从αβo静止坐标系到dqo旋转坐标系的旋转变换，α、β、o是由三相信号构造的。其变换结果，使αβ的工频信号在三相对称的情况下，变换成dq的直流信号。如果能在dqo旋转坐标系下对这个直流信号进行数字仿真，显然可以设定较大的仿真步长。

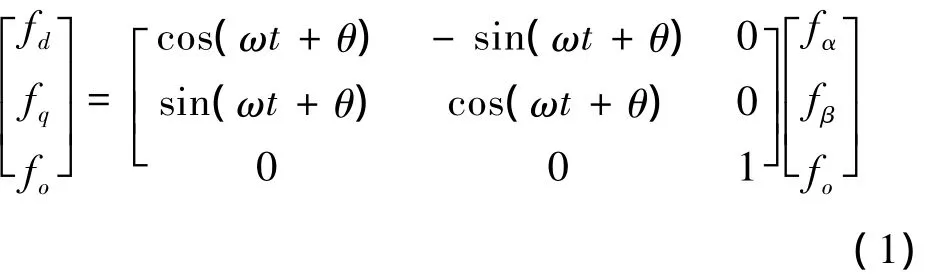
三相对称时o轴实际和其他2个轴是解耦的，此时式(1)可以简化成式(2)，即

由电机学知识可知，三相不对称时，静止坐标系下工频变化的量在发电机中会感应出不同频率的量，这时旋转坐标系下信号的频率反而比静止坐标系下的工频大得多，无法实现大步长。

本文借鉴上述思想，通过构造单相信号而不是三相信号的旋转变换实现信号频率的降低，并且没有上述的发电机问题，从而实现大步长的仿真。

1.1 复数信号的旋转变换

交流电网中，电压、电流x(t)是以工频为主导频率的正弦窄带信号，即

其相量形式为

如果幅值不满足准稳态条件，可用式(5)来描述:

式中A(t)表示信号的幅值包络。

信号的相量形式相应变为

在静止坐标系下，假设能够从x(ω，t)构造一个复数信号:

可以通过下面的变换建立Xdq(t)与Zxy(ω，t)间的关系:

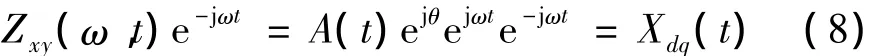
将式(8)按实部和虚部展开:

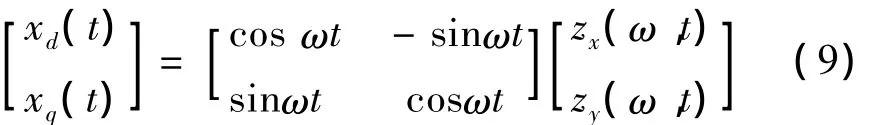
观察Xdq(t)与Zxy(ω，t)，式(9)实现了与式(2)相同的从静止坐标系x－y到旋转坐标系d－q的旋转变换，也即式(8)中e－jωt是一个旋转变换。在d－q旋转坐标系中，xd(t)=A(t)cosθ，xq(t)=A(t)cosθ，不再是直流信号，但是由于A(t)是x(t)的包络，其频率较低，可以采用大步长。

当系统的频率存在波动或偏差时，d－q坐标系的旋转频率ωr可以与信号频率ω不同，设:

对式(8)可做类似的旋转变换:

按实部和虚部展开:

当ω，ωr相差不大时，Δω是一个比较小的数，xd(ω，ωr，t)，xq(ω，ωr，t)是一个低频变化的量，式(12)、(13)实现的是快变信号与慢变信号间的旋转变换，仍然可以采用大步长。

值得注意的是，这里的旋转变换与式(1)、(2)的不同之处在于其是按单相进行的，因此没有Park变换中由于三相不对称负序产生倍频而影响仿真步长大小的问题。

1.2 复数信号构造

上述的变换实际是这样一个过程:

因此，关键是如何从一个实数信号x(t)构造出一个复数信号Zxy(t)。由于zx(ω，t)=x(t)，实际上就是如何构造出正交的zy(ω，t)。交流电网中，电压、电流即x(t)一般为正弦量，利用这一特点，可以有下面几种方法。

(1)积分变换。由于微分变换会对高次谐波放大。根据电力系统信号的特点，也可以采用积分变换来构造，即zy=ω∫zxdt。当含有谐波时，设

则:

从式(15)中可看出，谐波次数在分母上，因此，高次谐波的存在不会影响zx(ω，t)与zy(ω，t)的正交性，且谐波次数对数值影响不大。正常情况下，交流网中的谐波比例很小，系统的主导频率仍然是基波。因此，经过基波变换后zy与zx是近似正交的。

(2)Hilbert变换。在动态相量中用Hilbert变换来构造zy(ω，t)。其特点是能在各频次下保证实现zy与zx正交。但是由于Hilber变换是一个与原始信号的卷积，其计算量很大，影响了仿真速度。本文采用方法(1)来构造单相的复数信号。

2 大步长下基本元件的电磁暂态等值模型

可以用式(16)得到原信号x(t):

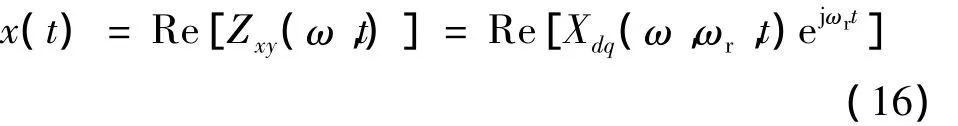
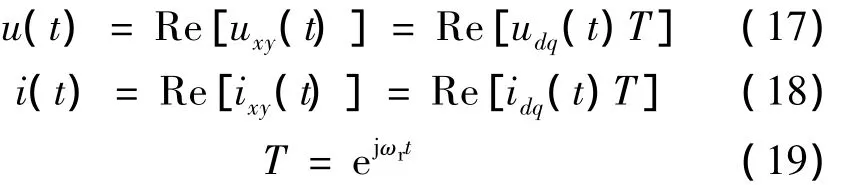
则电压和电流的实际信号u(t)、i(t)可用d－q下的复数信号还原。为了简洁，不再给出频率参数项，即:电磁暂态仿真中电力元件一般采用Dommel等值模型，下面推导d-q坐标系下各元件的Dommel等值模型。

2.1 电阻模型

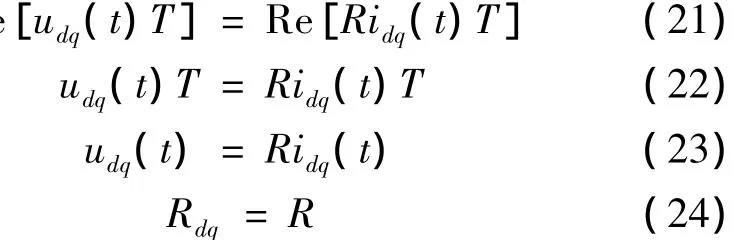
可见，在d-q坐标系下，电阻的形式与静止坐标系下一致。

2.2 电感模型

设RL=2L/h，ZL=RL+jωrL，YL=1/RL+jωrL ，Z*L=RL－ jωrL则式(31)可记为

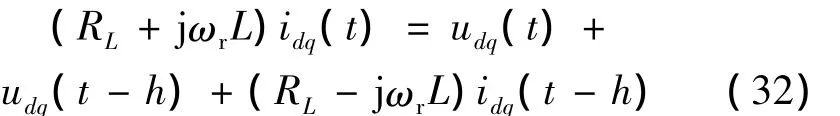
即

写成Dommel的等值形式:

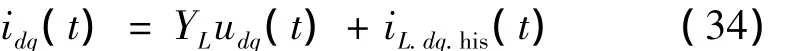
其中，iL．dq．his(t)=YLudq(t－ h)+表示历史电流。

需要注意的是，以上变量都为复数。

2.3 电容模型

与电感类似:

写成Dommel的等值形式:

其他设备如发电机、变压器、传输线、电动机等因为篇幅所限这里不一一推导。

3 电磁暂态仿真步长的选取

上面元件的公式中，由于出现了旋转频率ωr，随着ωr的取值不同，可以实现仿真步长的自适应调整。当需要详细仿真时，取ωr=0，即不旋转，仿真可以取小步长，当不需要详细仿真时，取ωr为主导频率50 Hz，变换到旋转坐标系下，可以取大步长。此外，ωr如果取次同步振荡的频率，还可以用来进行次同步振荡的仿真分析。一般，对于含有电力电子器件的FACTS、HVDC等装置时，由于其开关频率高，仿真可以取小步长，而对于常规的交流电网部分，其主导频率为工频，可以将旋转频率设为工频，通过旋转变换后，仿真可以取大步长。

实际上，以此为基础可以设计一种多速率的混合仿真方案。该方案中应该充分考虑如下几个因素:(1)如何方便地实现不同速率仿真的接口;(2)该接口是否易于实现不同速率仿真的并行计算;(3)采用何种高效的电网划分和并行计算方法。限于篇幅，这些研究将在后续文章中给出。

4 算例

这里给出IEEE14的仿真算例，以验证本文提出的大步长快速仿真的有效性，如图1所示。为了简化程序，其中发电机目前用等值电压源代替，线路用π型集中等值模型。

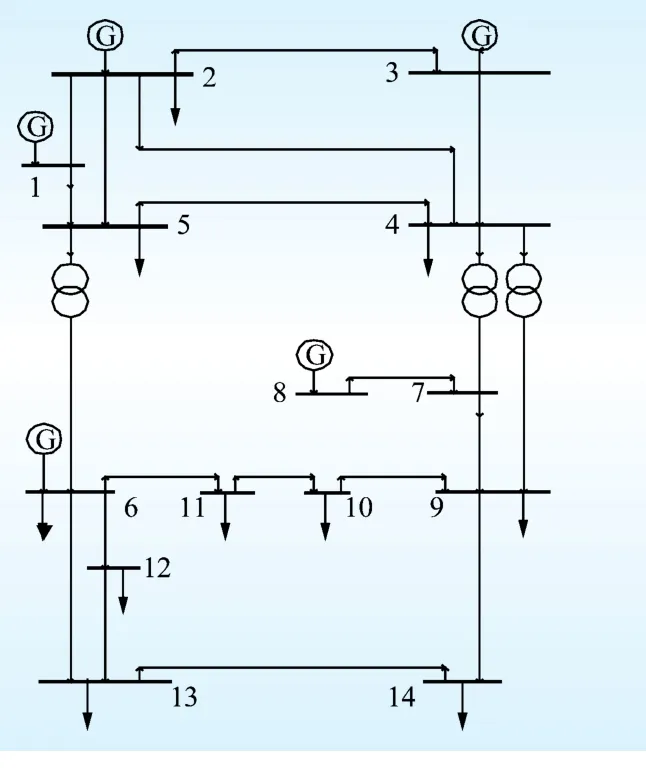
图1 IEEE 14节点系统图Fig.1 IEEE 14 node system

图2 是支路1－5首端电流的仿真结果。其中EMTDC表示的是采用PSCAD/EMTDC软件的仿真结果。小步长、大步长是本文程序采用不同仿真步长的结果。EMTDC的仿真步长为100 μs，小步长为100 μs，大步长为5 ms。图2(a)表示的是瞬时值，图2(b)是为了比较精度，对图2(a)的局部放大。从仿真结果可以看出，本文的仿真步长可以灵活设置，精度与PSCAD/EMTDC的精度近似一致。

5 结语

本文基于坐标系旋转变换的思想，提出了一种大步长的快速电磁暂态仿真方法。仿真算例表明本方法具有可行性。由于目前的工作尚处于初始阶段，发电机、传输线等模型的完善还需进一步开展。此外，基于该方法还可以实现一种多速率的混合方法，对含有电力电子装置或人为设定的部分采用小步长电磁暂态仿真，对于不需详细了解的交流网部分采用本文的大步长电磁暂态仿真。小步长和大步长间按一定的原则接口，可以方便地实现并行计算。这些工作留待后面继续深入研究。

［1］李亚楼，穆清，安宁，等．直流电网模型和仿真的发展与挑战［J］．电力系统自动化，2014，38(4):127-135．Li Yalou，Mu Qing，An Ning，et al．Development and challenge of modeling and simulation of DC grid［J］．Automation of Electric Power Systems，2014，38(4):127-135．

［2］王成山，李鹏，王立伟．电力系统电磁暂态仿真算法研究进展［J］．电力系统自动化，2009，33(7):97-103．Wang Cheshang，Li Peng，Wang Liwei．progresses on algorithm of electromagnetic transient simulation for electric power system［J］．Automation of Electric Power Systems，2009，33(7):97-103

［3］汤涌．交直流电力系统多时间尺度全过程仿真和建模研究新进展［J］．电网技术，2009，33(16):1-8．Tang Yong．New progress in research on multi-time scale unified simulation and modeling for AC/DC power systems［J］．Power System Technology，2009，33(16):1-8

［4］黄胜利．时变动态相量理论在电力系统分析中的应用［D］．北京:中国电力科学研究院，2002．Huang Shengli．Application of time-varying dynamic phasor theory in analysis of electric power system［D］．Beijing:China Electric Power Research Institute，2002

［5］鄂志君．基于动态相量理论的电力系统建模与仿真研究［D］．天津:天津大学，2008．Er Zhijun．Research on modelling and simulation of power system based on dynamic phasor［D］．Tianjin:Tianjing University，2008

［6］ Sebastian Henschel． Analysis of electromagnetic and electromechanical power system transients with dynamic phasors［D］．University ofBritish Columbia，City ofVancouver，Canada，1999．

［7］ Turhan，Simulation of power system dynamics using dynamic phasor models［D］．Swiss Federal institute ofTechnology，Zurich，Switzerland，2008．

［8］ Zhang P，Martí J R．Shifted-frequency analysis for EMTP simulation of power-system dynamics［J］．IEEE Transactionson on Circuits and Systems，2010，57(9):2564-2574．

［9］ Martí J R，Dommel H W，Bonatto B D，et al．Shifted frequency analysis(SFA)concepts for EMTP modelling and simulation of powersystem dynamics［C］//Power Systems Computation Conference(PSCC)，2014．IEEE，2014:1-8．

［10］Gao F，Strunz K．Frequency-adaptive power system modeling for multiscale simulation of transients［J］．IEEE Transactions on Power Systems，2009，24(2):561-571．

［11］Strunz K，Shintaku R， Gao F． Frequency-adaptive network modeling forintegrative simulation ofnaturaland envelope waveforms in power systems and circuits［J］．IEEE Transactions on Circuits andSystemsI:RegularPapers， 2006， 53(12):2788-2803．

［12］岳程燕，周孝信，李若梅．电力系统电磁暂态实时仿真中并行算法的研究［J］．中国电机工程学报，2004，24(12):1-7．Yue Cheyan， Zhou Xiaoxing， Li Ruomei． Study of parallel approaches to power system electromagnetic transient real-time simulation［J］．Proceedings of the CSEE，2004，24(12):1-7．

［13］岳程燕．电力系统电磁暂态与机电暂态混合实时仿真的研究［D］．北京:中国电力科学研究院，2004．Yue Chengyan．Study of power system electromagnetic transient and electromechanical transientreal-time hybrid simulation［D］．Beijing:China Electric Power Research Institute，2004．

［14］柳勇军．电力系统机电暂态和电磁暂态混合仿真技术的研究［D］．北京:清华大学，2006．Liu Yongjun．Study on power system electromechanical transient and electromagnetic transient hybrid simulation［D］．Beijing:Tsinghua university，2006

［15］张怡．基于频率相关网络等值的机电电磁暂态混合仿真研究［D］．北京:清华大学，2012，Zhang Yi．Study on frequency dependent network equivalent based electromagnetic and electromechanical transient hybrid simulation［D］．Beijing:Tsinghua University，2012

［16］刘文焯，侯俊贤，汤涌，等．考虑不对称故障的机电暂态–电磁暂态混合仿真方法［J］．中国电机工程学报，2010，30(13):8-15．Liu Wenzhuo， HouJunxian， Tang Yong． Electromechanical transient/electromagnetic transient hybrid simulation method onsidering asymmetric faults［J］．Proceedings of the CSEE，2010，30(13):8-15．

［17］张树卿，童陆园，薛巍，等．基于数字计算机和RTDS的实时混合仿真［J］．电力系统自动化，2009，33(18):61-66．Zhang Shuqing，Tong Luyuan，Xu Wei，et al．Digital computer and RTDS based real-time hybrid simulation［J］．Automation of Electric Power Systems，2009，33(18):61-66

［18］王文举．时域积分方程快速算法及并行计算的研究与应用［D］．长沙:国防科学技术大学，2009．Wang Wenjun．Study and application on fast algorithms of time domain integral equation and theirparallelalgorithms［D］．Changsha:National University of Defense Technology，2009．

［19］王路，李兴源，罗凯明，等．交直流混联系统的多速率混合仿真技术研究［J］．电网技术，2005，29(15):23-27．Wang Lu，Li Xingyuan，Luo Kaiming，et al．Study on multirate hybrid simulation technology for AC/DC power system［J］．Power System Technology，2005，29(15):23-27．

［20］陈来军，陈颖，许寅，等．基于GPU的电磁暂态仿真可行性研究［J］．电力系统保护与控制，2013，41(2):107-112．Chen Laijun，Chen Ying，Xu Yin，et al．Feasibility study of GPU based electromagnetic transient simulation［J］．Power System Protection and Control，2013，41(2):107-112．

［21］许寅，陈颖，陈来军，等．基于平均化理论的PWM变流器电磁暂态快速仿真方法:(一)PWM变流器分段平均模型的建立［J］．电力系统自动化，2013，37(11):58-64．Xu Yin，Chen Ying，Chen Laijun，et al．Fast electromagnetic transient simulation method for PWM converters based on averaging theory．Part one:Establishment of piecewise averaged model for PWM converters［J］．Automation of Electric Power Systems，2013，37(11):58-64．

［22］许寅，陈颖，陈来军，等．基于平均化理论的PWM变流器电磁暂态快速仿真方法:(二)适用PWM变流器分段平均模型的改进 EMTP 算法［J］．电力系统自动化，2013，37(12):51-56．Xu Yin，Chen Ying，Chen Laijun，et al．Fast electromagnetic transient simulation method for PWM converters based on averaging theory．Part two:Improved EMTP algorithm suitable for piecewise averaged model of PWM converters［J］．Automation of Electric Power Systems，2013，37(12):51-56．

［23］高海翔，陈颖，于智同，等．基于平均化理论的PWM变流器电磁暂态快速仿真方法:(三)适用于图像处理器的改进EMTP并行仿真算法［J］．电力系统自动化，2014，38(6):43-48．Gao Haixiang，Chen Ying，Yu Zhitong，et al．Electromagnetic transient simulation method for PWM converters based on averaging theory．Part three:Improved EMTP parallel algorithm for graphic processing unit［J］．Automation of Electric Power Systems，2014，38(6):43-48．

［24］穆清，李亚楼，周孝信，等．基于传输线分网的并行多速率电磁暂态仿真算法［J］．电力系统自动化，2014，39(7):47-52．MuQing，LiYalou， ZhouXiaoxin，et al． A parallel multi-rate electromagnetic transient simulation algorithm based on network division through transmission line［J］．Automation of Electric Power Systems，2014，39(7):47-52．

［25］高毅，李继平，王成山．基于变量自适应分组的电力系统多速率仿真算法［J］．电力自动化设备，2011，31(2):1-6，25．Gao Yi，Li Jiping，Wang Chengshan．Multi-rate method for power system simulation based on self-adaptive variable grouping［J］．Electric Power Automation Equipment，2011，31(2):1-6，25．

［26］Estep D，Ginting V，Tavener S．A Posteriori analysis of a multirate numerical method for ordinary differential equations［J］．Computer Methods in Applied Mechanics and Engineering，2012(223):10-27．

［27］ Chen J，Crow M．A variable partitioning strategy for the multirate method in power systems［J］． IEEE Transactions on Power Systems，2008，23(2):58 －266．

［28］Plumier F，Geuzaine C，van Cutsem T．A multirate approach to combine electromagnetic transients and fundamental-frequency simulations［C］//10th InternationalPowerSystem Transients conference．2013．

［29］ Zhou Z．Parallel electromagnetic transient simulation of large-scale power systems on massive-threading hardware［D］．University of Alberta，Alberta，Canda，2012．

［30］ Watson N，Arrillaga J．Power systems electromagnetic transients simulation［M］．IET，2003．