基于Bayes算法的垃圾邮件过滤

耿德志

（晋中学院信息技术与工程学院，山西晋中030619）

（编辑 张 瑛）

随着网络的多元化应用，人们进行信息通讯的首选工具正不断倾向于便捷、灵活、低成本的电子邮件，但因此产生的垃圾邮件也以较快的速度蔓延全球.垃圾邮件英文称为spam，也称为UCE（Unsolicited commercial Email，不请自来的商业电子邮件）或UBE（Unsolicited Bulk Email，不请自来的批量电子邮件）[1~2].垃圾邮件一般具有数目众多、带有商业目的、用户不想接收这三个基本特点，它造成的危害如下：过度消耗带宽；浪费用户时间；威胁网络安全.因此全球科学人员应该更深层次地对垃圾邮件过滤技术进行研究与探讨.垃圾邮件的不断蔓延也使人们更加体会到垃圾邮件过滤技术的重要性.

如何采用合理、科学的过滤算法对用户新接受邮件进行分类处理，并对分类结果为垃圾邮件的接收邮件进行有效过滤是识别垃圾邮件的核心问题[3].邮件用户代理过滤、邮件传输代理过滤、邮件投递代理过滤是根据电子邮件体系结构角色层次进行的划分[4~5].相比较而言，基于内容的过滤、基于黑白名单的过滤、基于规则的过滤等则是根据过滤技术层次进行的划分.

基于内容的垃圾邮件过滤结合了信息过滤[6]、文本分类等技术[7~9]，运用这些技术中的处理方法分析电子邮件中的内容，进而达到识别垃圾邮件的目的.其根据统计分类邮件内容的结果来处理新接收邮件.由于其速度快、过滤精度高，因此成为比较受欢迎的一种垃圾邮件过滤方法，如k近邻法（k-NN）、神经网络、贝叶斯算法.在众多垃圾邮件过滤技术中，性能稳定、准确精度较高的贝叶斯算法在行业应用中将其特点发挥得淋漓尽致.

本文核心内容是应用贝叶斯算法对垃圾邮件进行处理.通过信息反馈学习机制增强系统的准确性.

1 贝叶斯算法及过滤相关技术

1.1 贝叶斯定理

贝叶斯定理在已知过去事件发生概率的基础上推断未来事件发生的可能性，其可以通过相关数学运算得出未来事件发生的概率.贝叶斯定理表明概率是对不确定事件发生的一种映射.

垃圾邮件过滤可以理解成为一个将新接收邮件分为垃圾邮件或正常邮件的二值分类问题.因此可以根据正确分类的邮件，应用贝叶斯定理推断新接收邮件的类别.

贝叶斯定理的描述如下：样本空间K是一个随机实验E中一切可能基本结果组成的集合，并且K的一个子集为{B1，B2，…Br}.K中某一事件发生的概率采用数学符号表示为{P（A）|A■K}，则对于K中的任意事件 A、B，有 P（A）>0，P（B|A）=P（A∩B）/P（A）表示以 A 发生为前提，B 发生的条件概率.贝叶斯定理可表示为：

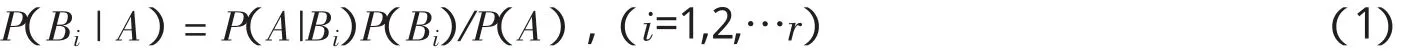
其中P（A）>0由全概率公式可得

式（1）中，P（Bi|A）为后验概率，P（A|Bi）为似然概率，P（Bi）为先验概率.

1.2 贝叶斯分类器

贝叶斯分类器可看成是文本分类特殊化与贝叶斯定理实例化的结合.文本分类的中心任务是：依据文本内容的解析结果，将文本与指定类别相关联.根据文本属于每个类别的概率计算结果，贝叶斯分类器会将其关联到概率最大的类别中.

在文本分类领域，表示文本一般采用向量空间模型机制（VSM，Vector Space Model），即文档实现向量化：d=（t1，w1；t2，w2；…tn；wn）或者d=（w1，w2…wn），ti是特征项，可以使用字、词作为特征项.wn（n=1，2，3…n）表示第n个特征项的权重，n是特征项的个数.权重的计算方法有很多，布尔权重、文档频次、字频、词频都可以作为权重使用.为了便于计算，本文特征项使用字作为标准，权重使用字频作为标准.另有变量C是类别集合{C1，C2…Cm}中的一个元素.对一待分类文本 dx=（x1，x2，…xn），则样本 dx属于类别 Ci的条件：

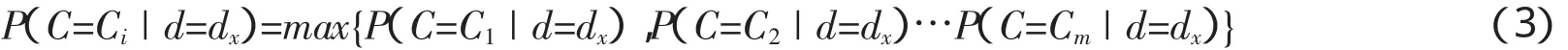
即将dx分类到概率最大的类别中，利用贝叶斯定理计算文本dx属于某个类别的概率为：

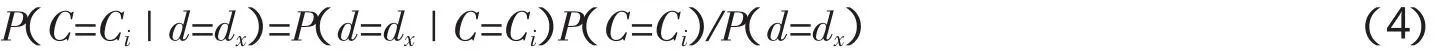
式中P（C=Ci）是Ci的先验概率；P（d=dx）是指试验中dx发生的概率，根据全概率公式得

对于同一文档P（d=dx）不会发生变化而且较易进行计算.P（d=dx|C=Ci）是似然函数，即指类Ci中dx发生的类条件概率.当面临较大数目的特征数以及依存度较高的特征变量时，此计算过于复杂.为降低计算难度，可假设各特征变量之间是独立的，因此出现了朴素贝叶斯分类器模型.

对于指定的分类变量C，假设各特征变量di之间相互独立，则有:

故而

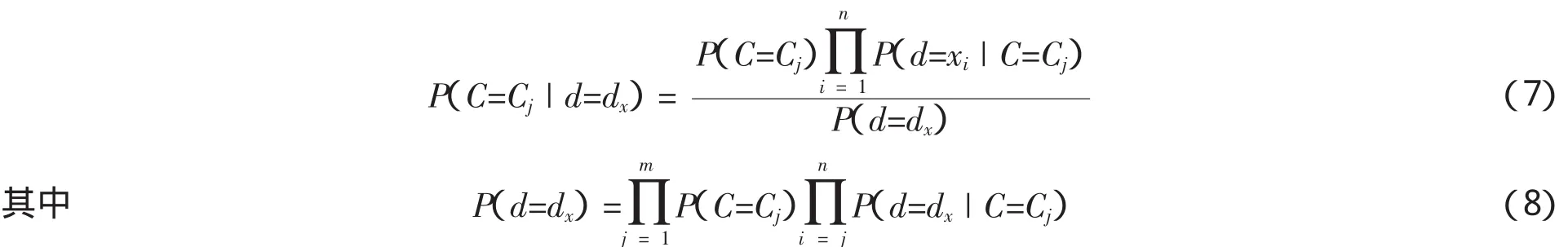
朴素贝叶斯分类器的结构如图所示：

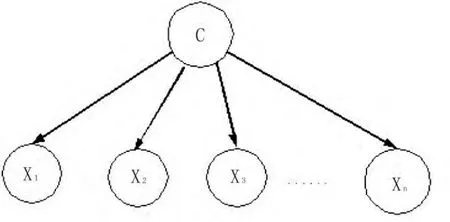
图1 朴素贝叶斯分类器结构图

1.3 贝叶斯过滤器

贝叶斯过滤器是贝叶斯分类器的特殊化.由于垃圾邮件过滤问题是文本分类的一个特例，因此可以将文本分类思想引入到构造贝叶斯过滤器的过程中.

收集整理一个垃圾邮件集，该集合由两部分组成.第一部分作为贝叶斯过滤器训练的题材，训练前需要人工分类题材.第二部分在测试贝叶斯过滤器效果时使用.过滤流程：（1）在训练样本集的基础上提取特征项，建立特征集合，依据特征集合中的特征，向量化处理测试样本集中的邮件.（2）以邮件特征为依据，分别统计训练集上每个类别中类的先验概率和每个特征的类条件概率.（3）综合考虑特征条件概率和类先验概率，计算新接收邮件属于每个类别的概率.（4）基于相似度对邮件作出相应分类.

数学描述：使用 VSM模型处理每一封样本邮件，其数学表示为 d=（t1，w1；t2，w2，…tn，wn），ti是邮件选取的特征项，wi是ti的权重，邮件类别标签为：C={Spam，Ham}.贝叶斯分类器的核心是计算新接收邮件是垃圾邮件的概率，然后将其与设定的阈值进行比较，一旦超过则被判定为垃圾邮件.假设一封新邮件dx=（x1，x2，…xn）依据贝叶斯算法，计算新接收邮件属于垃圾邮件的概率公式：

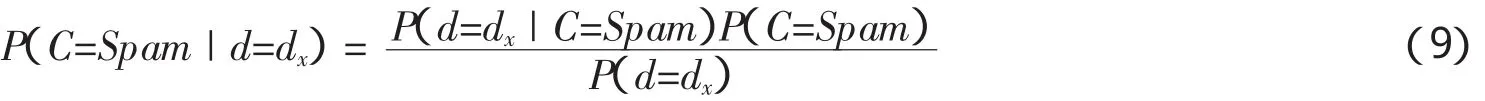
其中P（d=dx|C=Spam）指在类别为垃圾邮件的前提下，dx中所有特征项同时出现的概率；P（C=Spam）指类别为垃圾邮件的概率.根据P（d=dx|C=Ham）与阈值的比较结果即可确定邮件类型.

1.4 贝叶斯过滤器模型关键技术

1.4.1分词

对文本分词处理即按照句中词的含义对句子进行词汇分离，分离出的每个词汇为一个可识别的Token单元.贝叶斯过滤器的效果与分词算法有着密切的联系.由于英文文本相邻构成元素之间区分度较大，因此有利于方便处理.相比较英文邮件处理，处理中文邮件则需要洞察中文词汇的特点，才能实现合理分词.

1.4.2特征选择

随着邮件不断积累，训练集中词汇量逐渐加大，由这些特征词组成的向量维数也会相应剧增，给计算施加了较大压力.在分离出的特征词中，有些对区分邮件类别所起到的作用微乎其微，可以忽略其影响.特征提取的目的是为了减少向量空间维度，降低计算难度，这就需要最大程度上移除特征集中可忽略其影响效果的特征词汇.

进行特征选词的一般方法：对文本进行向量化处理，移除特征集中可忽略其影响效果的特征词汇.依据一定的评价函数计算特征词与类的相关概率，为提高分类器的精度，根据计算结果选取定量较优的特征词.常用的特征提取方法：文档频度、信息增益等.

由于较少特征量不但会致使区分效果不显著，也会减弱邮件表达的含义.而过度的特征量会给邮件分类带入相关次要影响，因此对于邮件特征的提取，其数量应该适中.实验数据表明：英文语料库的最佳特征集合大小范围为350～800；中文语料库的最佳特征集合大小范围为1 200～1 800.

2 功能模块分析

2.1 系统基本功能

本系统基本功能是对用户新接受邮件进行分类判定，并对其中的垃圾邮件进行有效过滤.本系统可以通过自学习用户判定的垃圾邮件来加强系统的适应性，降低系统误判率.

2.2 结构设计

自学习模块：本模块中用户主动选择垃圾邮件库与正常邮件库的保存路径，垃圾邮件库中保存之前逐渐积累的垃圾邮件和当前下载邮件中用户根据自己意愿所判定的垃圾邮件.正常邮件库中保存用户之前积累的合法邮件.该模块会处理垃圾邮件库与正常邮件库中的邮件，将这些邮件中分离的词汇扩充到相应的词汇库中，完成对垃圾邮件库与合法邮件库的加载过程.此外，在本模块中可以设定判断垃圾邮件的阈值，该阈值默认设置为0.9.

用户登录模块：通过用户手工输入一些基本信息（如：邮箱类型、电子邮箱账号、密码）进行邮箱网络验证.此模块验证用户输入邮箱信息的有效性，保证本系统可以顺利登陆用户邮箱，为邮件下载模块提供先前条件.

邮件下载模块：本系统顺利登陆用户电子邮箱后，该模块会查询用户邮箱中邮件总数，并对其中的电子邮件进行下载.下载界面底部初始化会显示邮件总量，当下载开始后，底部则会显示每一封邮件的下载进度.在下载界面的中心部分会相应显示当前下载邮件的主题、发件人、收件人、下载路径等邮件的相关信息.对于界面中心显示的邮件，如果用户想查看邮件内容，本系统通过调用Microsoft officeoutlook进行实现.用户可以根据自己的意愿判定所显示邮件的类型即判定界面所列邮件为垃圾邮件还是正常邮件.系统在自学习模块中会主动学习用户积累的垃圾邮件.当然，用户也可以删除个别下载的邮件.

垃圾邮件过滤模块：本模块包含三个较小的模块，分别为邮件解析模块、邮件分词模块、邮件过滤模块.

邮件解析模块：由于网络上传输信息是以base64进行编码的，所以下载的电子邮件需要进行base64解码，否则邮件内容不能正常显示，这会妨碍邮件分词功能的实现.在邮件解析模块中会对下载的邮件进行base64解码，实现文本正常显示，为邮件分词模块铺就道路.

邮件过滤模块：本模块会对分词模块中分离的词汇进行概率计算，然后根据自学习模块中加载的数据字典进行相关概率计算.通过计算分离词汇同时出现在新接收邮件中的概率，并将此概率与设定阈值进行比较来确定邮件类型，最终依据识别的邮件模块——本模块会对邮件的相关信息（如文本内容）进行分词处理，用以判定电子邮件的类型.类型作出相应处理，在删除垃圾邮件之前，该模块会将垃圾邮件中分离出的词汇保存到词汇库中，扩大词汇量，提高系统判定垃圾邮件的准确率.

3 基于贝叶斯算法的垃圾邮件过滤

基于贝叶斯算法的垃圾邮件过滤步骤如下：

（1）基于积累的垃圾邮件与合法邮件，建立合适的训练集.

（2）对两个集合中全部邮件进行分词处理，分离出的独立字符串作为TOKEN串并统计其字频.

（3）将邮件集中的内容映射到相应的哈希表中，合法邮件集关联名为ham的哈希表，垃圾邮件集则关联名为spam的哈希表.

（5）综合考虑ham和spam这两个哈希表，根据表中TOKEN串出现的概率，计算新接收邮件当其文本中出现某TOKEN串时为垃圾邮件的概率.数学表达式为：

则

式中A表示邮件类别为垃圾邮件，ti代表某TOKEN串，P（A|ti）表示邮件文本中出现ti为A事件发生的概率.

（6）建立新的哈希表pro存储TOKEN串ti到P（A|ti）的映射.

（7）上述过程已经完成加载垃圾邮件集与合法邮件集的过程.根据哈希表，推断新接收邮件为垃圾邮件的概率.对新接受邮件按照上述过程分离出TOKEN串.查询pro得到该TOKEN串的键值.

假设由该邮件共得到 n 个 TOKEN串，t1，t2…tn，pro中对应的值为 P1，P2，…Pn，P（A|t1，t2，t3…tn）表示 TOKEN串t1，t2…tn同时出现在邮件中时，该邮件为垃圾邮件的概率.由复合概率公式可得

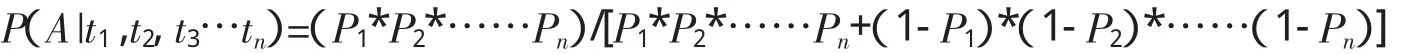
当 P（A|t1，t2，t3…tn）与预定阈值比较后时即可确定邮件类型.

4 系统实现

基于Bayes的垃圾邮件过滤系统包含系统自学习、邮箱登陆、邮件的下载、过滤等功能模块，每个功能模块的具体系统实现如下.

4.1 系统自学习

在该界面用户需要选择垃圾邮件集与合法邮件集的保存路径，如果未对其进行选择，系统会提示相关信息，方便用户使用.系统会加载用户选择的垃圾邮件集与合法邮件集，将数据字典映射到相应哈希表中，为垃圾邮件过滤功能提供先前条件.

4.2 邮箱登陆

在系统初始化界面的菜单栏中有文件选项，单击该选项会出现登陆选项.在POP3邮箱服务器下拉框中选择相关的服务器名称，其余的需要输入一些邮箱的相关信息（如邮箱名称、密码），登陆界面上的相关信息都必须填写，否则会出现相应提示.当相关信息填写完成后，通过socket进行网络信息验证.

4.3 邮件下载、过滤

用户成功登录邮箱之后，系统会对邮箱中的电子邮件进行下载，下载进度会在界面底部显示出来，邮件有关信息会在界面中心进行显示.用户可以查看、删除界面中心所列的电子邮件.用户可以根据自己的意愿对邮箱中的邮件进行分类，系统会将用户所分类邮件进行标记处理并放到相应文件夹中以备系统自学习使用.在该界面中当邮件被识别为合法邮件时状态栏会显示对号，否则会显示叉号.

5 结束语

垃圾邮件的多方面变化致使垃圾邮件过滤技术相应地呈现多样化的特点.通过解析邮件文本内容洞察出发件者的意图，并据此分类过滤邮件.本文采用基于贝叶斯算法对用户新接受邮件进行分类处理，根据用户判定的垃圾邮件进行自学习以此来增强系统对垃圾邮件判定的准确率，并对分类结果为垃圾邮件的接收邮件进行有效过滤.与传统的其他过滤办法（如K近邻法k-NN、神经网络）等相比，贝叶斯算法是通过计算特征库中存储的词汇同时出现在新接收邮件中的概率，并将此概率与设定阈值进行比较来确定邮件的类型，此方法过滤效果显著、处理时间短、消耗内存小、适应能力强，可帮助用户过滤其不想接收的垃圾邮件（如广告邮件、销售邮件等），为用户提供一个安全可靠的邮箱环境，并在一定程度上缓解了网络负担.

［1］Meds Haahr and Alan Gray.Personalized Collaborative Spam Filtering［J］.In Proceedings of the First Conference on Email and Anti-Spam（CEAS），2004.

［2］L.F.Cranor，B.A.LaMacchia.Spam!［J］.Communicationsof the ACM，1998，41（8）：74～83.

［3］桂小林，陈菲菲.基于机器学习的动态信誉评估模型研究［J］.计算机研究与发展，2007（2）：200～239.

［4］赵焕彦.面向安全电子邮件的真实IPv6源地址验证机制设计与实现［D］.沈阳：东北大学，2008.

［5］李卓桓，陈勇.反垃圾邮件完全手册［M］.北京：清华大学出版社，2006.

［6］王永成.一种高效的中文电子词表数据结构［J］.计算机研究与发展，2000（1）：107～120.

［7］李东艳.一个基于非法文本用词特征分析的文本分类器［J］.电脑开发与应用，2006，19（10）：2～3，6.

［8］汪维家，秦进.文本分类中的特征提取［J］.计算机应用，2003，23（2）：41～48.

［9］尹存燕，赵伟.一种规则与统计相结合的汉语分词方法［J］.计算机应用研究，2004（3）：20～24.