改进的高度计海况偏差估计参数模型研究❋

苗洪利， 王 鑫， 王桂忠， 张国首， 张 杰

(1.中国海洋大学信息科学与工程学院，山东 青岛 266100； 2.国家海洋局第一海洋研究所，山东 青岛 266061)



改进的高度计海况偏差估计参数模型研究❋

苗洪利1， 王 鑫1， 王桂忠1， 张国首1， 张 杰2

(1.中国海洋大学信息科学与工程学院，山东 青岛 266100； 2.国家海洋局第一海洋研究所，山东 青岛 266061)

本文基于JASON-2雷达高度计共144个周期的8640万个数据，按照距离加权平均法对其进行共线处理。采用直接估计的方法得到海况偏差(SSB)，以此为真值，利用最小二乘法，对有效波高(SWH)和风速(U)的32种参数模型进行拟合并筛选，获得最优海况偏差估计参数模型。将最优参数模型应用于中国HY-2高度计，并与HY-2采用的传统SSB估计参数模型结果比较。结果表明：改进后的SSB估计参数模型有效，优于传统SSB参数模型。

卫星高度计；海况偏差；参数模型；有效波高；风速

卫星雷达高度计能够获得全球海表面高度(SSH)、有效波高(SWH)和风速(U)等信息[1]。海表面高度要经过诸多误差校正[2-6]。随着定轨技术的提高，海况偏差(SSB)已取代轨道误差而成为第一误差源[7]。SSB估计的理论模型由于难以获得所需参数而无法实用[8-12]。目前，普遍使用的是经验模型，分直接估计方法、参数模型和非参数模型。参数模型原理简单、建模直观、外延性好，可以适用于正常范围内任意有效波高(SWH)和风速(U)[13-14]。传统的参数模型使用SSH、SWH和U各自的卫星轨迹交叉点不符值回归模型系数，并非真正的SSB最小二乘拟合[15]，使得模型系数存在较大误差，降低了模型的精度。非参数模型是基于核平滑统计技术，不指定具体函数形式。采用大量数据构建权重矩阵，结果精度相对较高。但其建模过程复杂，运算量庞大，效率较低，应用时需要对模型结果构成的SSB查询表作双线性插值计算，因此，非参数模型的外延性较差。直接估计方法[16]采用众多周期的共线数据，参与计算的数据量庞大，其结果精度较高，但在使用时与非参数模型一样，需要双线性插值查表，外延性受限。

本文将传统的参数模型与直接估计方法结合，采用较高精度的SSB直接估计结果作为海况偏差真值，直接使用SWH和U值，利用真正意义的最小二乘法回归拟合参数模型系数，得到改进的参数模型，既保持了模型的外延性，又有效提高了模型精度。

1 建模原理

未校正的海表面高度测量值SSH′可以表示为:

SSH′=SSB+hg+η+ε′。

(1)

其中：hg为大地水准面高度；η为海表面动力高度；ε'为除SSB之外的所有测高误差之和，包括轨道误差、仪器误差和其它地球物理校正误差。

对交叉点之间不同时间的测量值进行差分，则公式(1)可表示为：

ΔSSH′=ΔSSB+Δη+Δε′。

(2)

其中ΔSSH′称为交叉点处海表面高度不符值，它消除了所有不随时间改变的信号部分，如大地水准面，动力地形的定常部分等。Δη是海表面动力高度的变化量。在JASON-2数据集中，升轨和降轨在交叉点处平均时间间隔为3.5d，Δη在此短时间间隔内的变化一般是很有限的。

参数模型基于SSB与SWH线性相关这一基本假设，则SSB参数模型可写为：

SSB=b(X,θ)SWH。

(3)

其中：b是一个无量纲的负值，称为海况偏差系数；X是与海况相关的变量组成的向量；θ是系数向量。在以往的经验研究中，X一般直接从高度计测得的与海况相关的变量中选取，即有效波高SWH、风速U或后向散射系数σ0以及它们的组合。由于U和σ0具有高度相关性(通常用σ0反演U)，因此，两者只能选其一。本研究选择使用U。将b对SWH和U进行泰勒展开到二阶，则可得到如下形式的SSB参数模型：

SSB=SWH[a1+a2SWH+a3U+a4SWH2+
a5U2+a6SWH·U]+εSSB，

(4)

进一步表示为如下形式：

(5)

其中：εSSB为SSB参数模型所不能解释的SSB信号部分；Xi为公式(4)中的变量；ai为变量Xi对应的系数。则公式(2)变为：

(6)

将所有误差合并为平均值为零的噪声ε的和，则上式可重新表示为：

(7)

假定噪声ε满足高斯-马尔柯夫条件和正态分布条件，那么此问题成为一个典型的多元线性回归问题。给定n组(ΔSSH′,ΔX)观测值，则系数的最小二乘估计为：

(8)

如果ΔX和ε不相关，则估计量无偏。将得到的回归系数带入公式(4)即完成参数模型的建立。

以上即为传统参数模型的建模原理及系数回归过程，由于缺乏SSB真值，建模采用交叉点升降轨SSH、SWH、U各自两组值平差得到不符值，确定模型系数。但是采用ΔSSH′建模而不是SSB真值，确定的各项系数均不是对SSB的真正最小二乘拟合，会带来较大误差。本研究从公式(5)出发，采用共线处理后的直接估计SSB值作为真值，并用与之对应的SWH和U值进行最小二乘拟合模型系数。有效消除了公式(6)中(Δη+Δε′)的误差影响。

2 模型建立

2.1SSB真值确定

卫星多重复周期的实际测量点经纬度信息并不完全一致。选用一条最优参考轨迹并确定该轨迹上各测量点为参考点。数据的共线处理是将不同周期相对于参考轨迹逐个参考点最近的4个实测点数据进行距离加权平均，求算共线SSHcoll、SWHcoll、Ucoll。由于每个实测点时间间隔为1s、距离7km左右，4个点的最大时间间隔为3s。有效波高和风速虽然随时间变化，但这样短的时间内可以认为基本恒定，共线处理的实质是将多重复周期的数据测量点经纬度信息做到全部统一[16]。

再将不同周期、相同PASS的同一参考点处SSHcoll求均值得到平均共线海表面高度MSSHcoll。

(9)

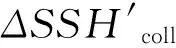
(10)

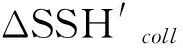
(11)

选用JASON-2高度计第1～144cycle数据，近8640万组。筛选保留SWHcoll(0～11m)及Ucoll在0～21m/s)内的数据并做共线处理。选取SWHcoll、Ucoll的初值分别为0.125m、0.125m/s、间隔为0.25m、0.25m/s，将数据分包网格化，得到SSBD查询表。存储格式见表1所示。

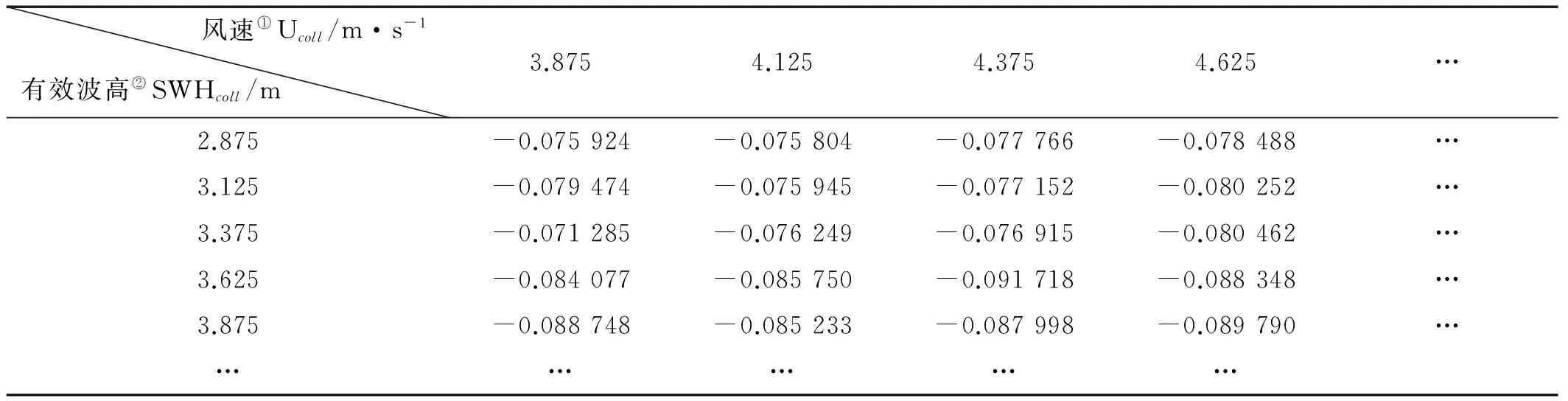
表1 SSBD直接估计查询表(示例)

Note：①Wind speed；②Significant wave height

任意测量点的SSBD估计通过查询表双线性插值获得。尽管通过查询表可以进行海况偏差SSB估计，并具有一定的精确度。但由于外延性较差，超出表中SWH和U的SSB无法获得，加之查表方法不够快捷方便，因此，我们只是将这一结果作为参数模型的函数真值，建立改进后的参数模型。

2.2 改进参数模型系数的确定

传统参数模型基于(7)式进行最小二乘拟合，而改进的参数模型使用(5)式，实现真正意义的关于SSB的最小二乘拟合。将表1中SSBD直接估计结果作为真值，将相应分包SWHcoll、Ucoll的中值及其组合作为X，给定n组(SSBD,X)值，则系数的标准线性最小二乘估计为：

(12)

如果X和εSSB不相关，则估计量无偏。公式(4)所表达的模型按包含变量个数可以分为6组，各组模型均保留常数项a1，依次增加变量的个数，则可以得到1个常数模型，5个二参数模型，10个三参数模型，10个四参数模型，5个五参数模型，1个六参数模型，共计6组32种形式，计算结果如表2所示。

2.3 模型的优选

将32种模型系数逐一代入(4)式，将直接估计SSB所对应的SWH和U输入模型得到模型结果。计算残差εSSB，并得到残差平方和SSEεSSB及残差的标准差StdεSSB(见表2)。SSEεSSB和StdεSSB均能表达模型的有效性和精度。SSEεSSB越小，回归平方和就越大，模型拟合优度R2就越大，模型估计的SSB值越接近真值，模型越有效。StdεSSB越小，模型精度越高。将SSEεSSB和StdεSSB从1～6参数分组平均，变化曲线见图1。可以看出，随着参数的增多，SSEεSSB和StdεSSB均在减小，选择六参数为最优模型，改进后的参数模型为：

SSB=SWH(-0.029 763+0.003 653SWH-

0.002 514U-0.000 546SWH2-0.000 023 27U2+

0.000 350 9SWH·U)

(13)

图1 SSEεSSB和StdεSSB变化曲线

3 模型应用与分析

3.1 模型应用

目前，中国HY-2高度计SSB估计采用的是传统参数模型。本文采用改进后的参数模型(13)式对HY-2第71cycle进行海况偏差SSB估计，结果如图2、3所示。可以看出，均是厘米级的负值，绝大部分在-50～-1cm之间。

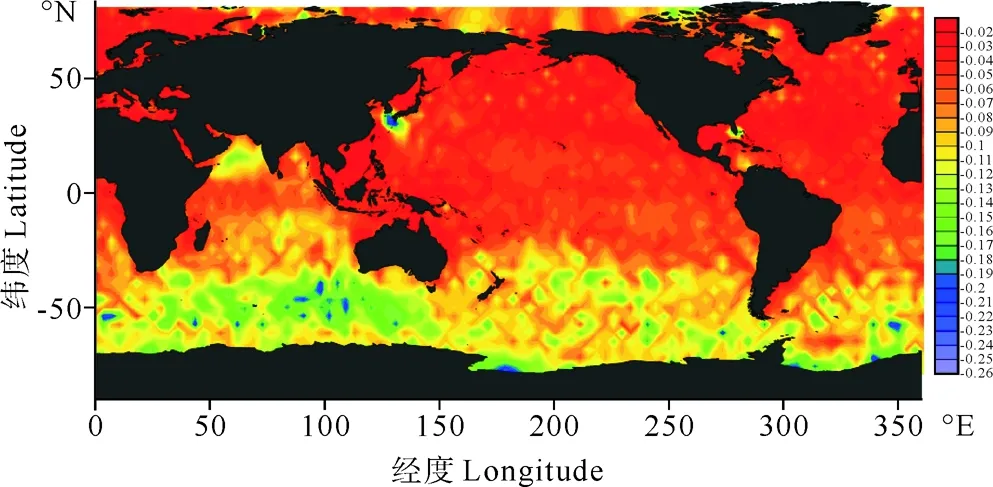
图2 改进参数模型在HY-2第71cycle的SSB值全球分布(m)

图2表示SSB模型结果的全球分布。可以看出，南半球的SSB绝对值大于北半球，主要是由于南半球海洋面积更广，没有大范围陆地而导致海况相对较强。也可以看到，高纬度地区相对低纬度地区SSB结果相对较大，说明高纬度地区由于西风带等影响导致有效波高和风速值均高于低纬度地区。

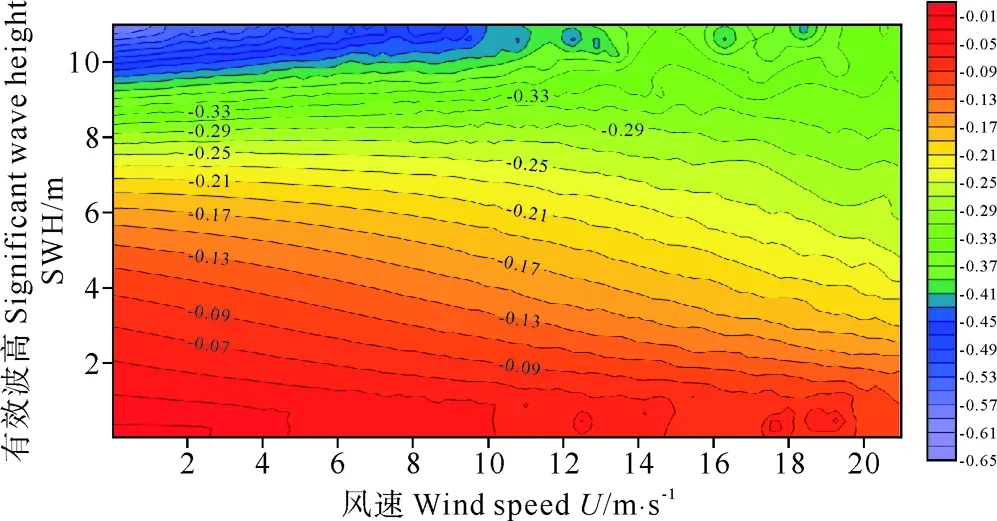
图3 改进参数模型在HY-2第71cycle的SSB值在(SWH,U)平面内分布(m)

图3为SSB在SWH、U二维平面内分布。可以看出，SSB与SWH、U均存在相关关系，随SWH和U的增大，SSB绝对值呈现增大趋势，而且，有效波高对SSB的影响要强于风速的影响。

表2 32种参数模型系数

3.2 分析与评价

将改进的模型估计结果SSBPM与HY-2GDR发布的估计结果SSBGDR进行分析比对，用以评价改进参数模型的有效性。将目前HY-2使用的模型视为传统参数模型。3.2.1 差异分析 对2种SSB估计结果进行拟合，散点图如图4所示，可见SSBPM与SSBGDR高度正相关，整体数据分布一致。但SSBPM的绝对值要大于SSBGDR的绝对值，从二者作差ΔSSB=SSBGDR-SSBPM的密度分布也同样看到差异。利用全局标准偏差S，求算差异量，计算公式如(14)式：

(14)

经过计算，S为1.8cm，相对偏差为13%，结合图4、5，改进的参数模型总体SSB估计量绝对值高于传统参数模型SSB估计量绝对值1.8cm。

(15)

图4 SSBPM与SSBGDR拟合散点图Fig.4 Fitting between SSBPM and SSBGDR

图5 ΔSSB的概率密度分布图Fig.5 Distribution of ΔSSB

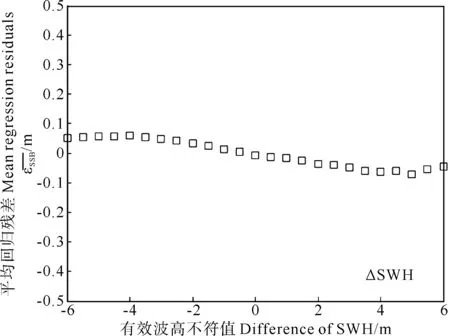
图6 改进模型 εSSB随ΔSWH变化Fig.6 εSSB rely on ΔSWH in PM123456

图7 改进模型εSSB随ΔU变化Fig.7 εSSB rely on ΔU in PM123456

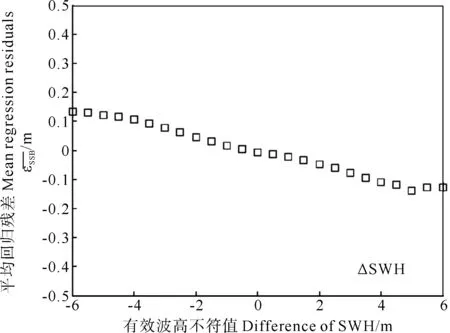
图8 传统模型εSSB随ΔSWH变化

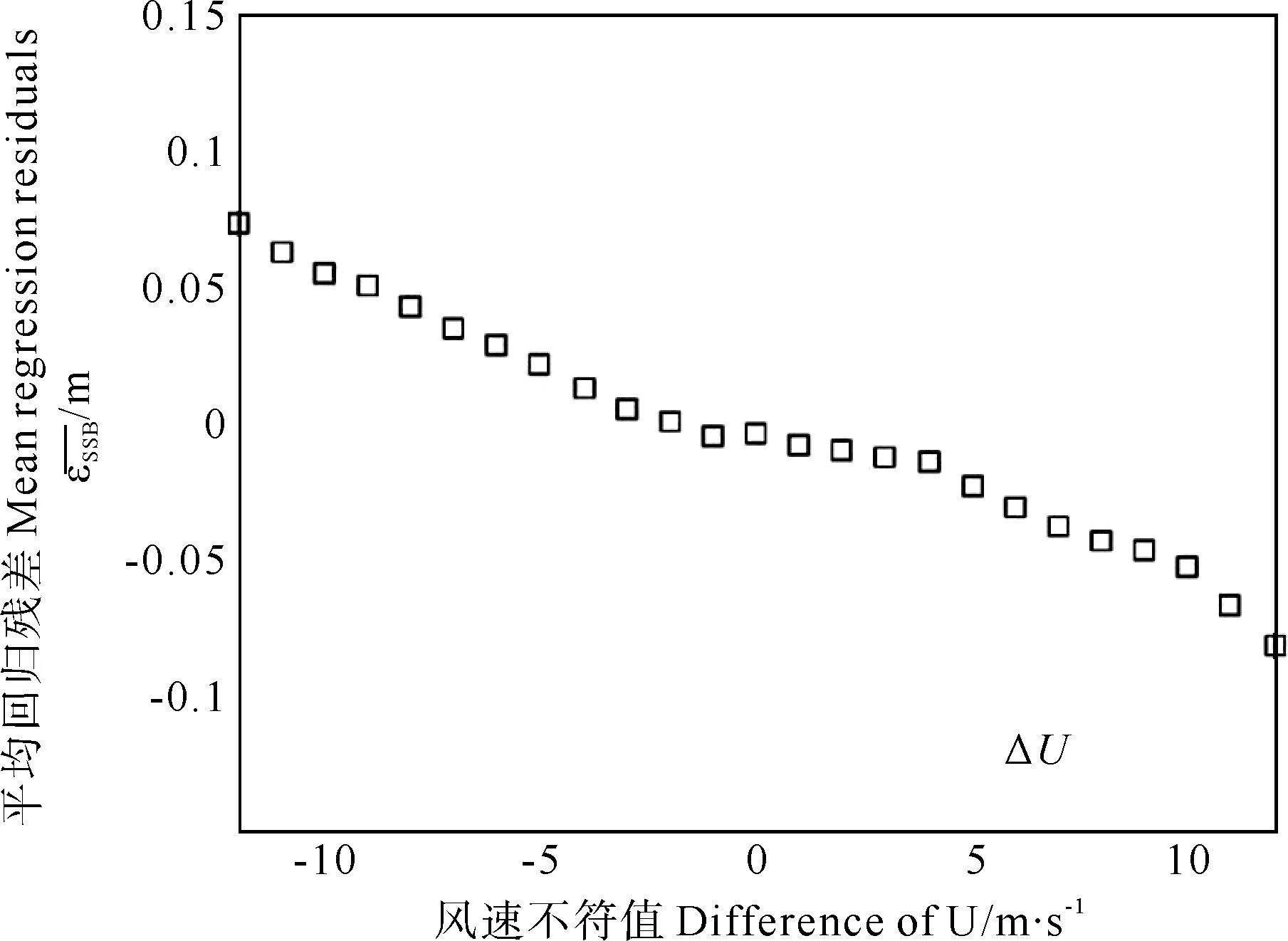
图9 传统模型εSSB随ΔU变化

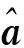
4 结语

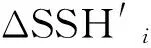
[1] Fu L L, Anny C. Satellite altimetry and earth sciences: a handbook of techniques and applications [M]. New York: Academic Press, 2001: 57-64.

[2] Yaplee B S, Shapiro A, Hammond D L, et al. Nanosecond Radar Observation of the Ocean Surface from a Surface from a Stable Platform[J]. IEEE Transactions on Geoscience Electronics, 1971, 9(3): 170-174.

[3] Jackson F C. The reflection of impulses from a nonlinear random sea [J]. Journal of Geophysical Research, 1979,84：190-196.

[4] Barrick D E, Lipa B J. Analysis and interpretation of altimeter sea echo [J]. Adv Geophys, 1985, 27: 60-99.

[5] Srokosz M A. On the joint distribution of surface elevation and slopes for a nonlinear random sea, with an application to radar altimetry [J]. Journal of Geophysical research, 1986, 91: 995-1006.

[6] Rodriguez E, Kim Y, Martin J M. The effect of small-wave modulation on the electromagnetic bias [J]. Journal of Geophysical Research, 1992, 97: 2379-2389.

[7] Elfouhaily T, Thompson D R, Chapron B, et al. Improved electromagnetic bias theory [J]. Journal of Geophysical Research, 2000, 105: 1299-1310.

[8] Glazman R, Fabrikant A, Srokosz M. Numerical analysis of the sea state bias for satellite altimetry [J]. Journal of geophysical Research, 1996, 101: 3789-3799.

[9] Elfouhaily T, Chapron B, Katsaros K, et al. Weakly nonlinear theory and sea state bias estimations [J]. Journal of Geophysical Research, 1999, 104: 7641-7647.

[10] Labroue S, Gaspar P, J Dorandeu, et al. Non parametric estimates of the sea state bias for the JASON-1 radar altimeter [J]. Marine Geodesy， 2004, 27 (3-4): 453-481.

[11] Arnold D, Kong J, Melville W. Physical optics prediction of EM bias [J]. Progress in Electromagnetic Research, 1989: 25-26.

[12] Warnick K F, Millet F W, Arnold D V. Physical and geometrical optics for 2-D surface with power-law height spectra [J]. IEEE Tranasctions on Antennas and Propagation, 2005, 53(3): 922-932.

[13] Gaspar P, Ogor F, Le Traon P-Y, et al. Estimating The Sea State Bias of the TOPEX and POSEIDON Altimeters from Crossover Differences[J]. Journal of Geophysical Research, 1994, 99(C12): 24981-24994.

[14] Gaspar P, Florens J P. Estimation of the sea state bias in radar altimeter measurements of sea level; Results from a new nonparametric method[J]. Journal of Geophysical Research, 1998, 103(C8): 15803-15814.

[15] Gaspar P, Labroue S, Ogor L, et al. Improving nonparametric estimates of the sea state bias in radar altimeter measurements of sea level[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19: 1690-1707.

[16] Van demark D, Tran N, Beckley, et al. Direct estimation of sea state impacts on radar altimeter sea level measurements[J]. Geophysical Research Letters, 2002, 29(24): 48-52.

责任编辑 陈呈超

Study on the Improved Sea State Bias Parametric Estimation Model

MIAO Hong-Li1, WANG Xin1, WANG Gui-Zhong1, ZHANG Guo-Shou1, ZHANG Jie2

(1.College of Information Science and Engineering, Ocean University of China, Qingdao 266100, China; 2.First Institute of Oceanography of State Oceanic Administration, Qingdao 266061, China)

The data of the 144 cycles was processed using the weighted distance method from JASON-2 Radar altimeter. The sea state bias (SSB) were gained by the direct estimation method and considered them to be the true values. Then we get the 32 different parametric models by using the method of least squares regression based on the significant wave height (SWH) and the wind speed (U). The optimal model is found by operation and filtration. The model is applied to the HY-2 Radar altimeter of China. After contrasted with the previous model in HY-2 it shows that the improved SSB parametric estimation model is efficient and better than the previous SSB parametric estimation model.

satellite altimeter; sea state bias; parametric model; significant wave height; wind speed

国家自然科学基金项目(41176157)；国家自然科学基金青年基金项目(41406197)资助

2015-04-10;

2015-07-10

苗洪利(1964-)，男，教授，主要从事海洋遥感方面的研究。E-mail:oumhl@ouc.edu.cn

TP79；P405

A

1672-5174(2015)12-119-07

10.16441/j.cnki.hdxb.20150125