NSCT域红外图像改进非局部均值滤波算法

韩红光



NSCT域红外图像改进非局部均值滤波算法

韩红光

（浙江农业商贸职业学院基础教学部，浙江 绍兴 312088）

结合非下采样轮廓波变换（NSCT），提出了一种红外图像改进非局部均值滤波算法（Improved Non-local Means Filtering，INLMF）。该算法首先对红外噪声图像进行多尺度NSCT变换，其次分别从相似图像块自适应划分方法以及滤波权重计算方法2个方面对经典非局部均值滤波算法进行适当改进，将改进后的非局部均值滤波算法（INLMF）应用于处理高频分解系数，然后将滤波后的高频分解系数与低频分解系数进行重构，得到去噪后的图像，最后对去噪后图像采用非负支撑域有限递归逆滤波（Non-negativity and Support Constraints Recursive Inverse Filtering，NAS-RIF）算法进行图像复原，以尽可能消除因滤波造成的图像失真。测试结果表明，本文算法滤波效果优于NLMF及其已有的改进算法。

红外图像处理；非下采样轮廓波变换；非局部均值滤波；非负支撑域有限递归逆滤波算法

0 引言

NSCT变换不仅具有Contourlet变换所具有的多分辨、多方向性的图像表达特性，而且具有平移不变以及方向选择的特点，由于NSCT相对于小波变换而言对于图像细节信息的刻画更为精细，因而在图像融合[1]、图像目标识别[2]、图像去噪[3]等方面得到了大量研究。

非局部均值滤波算法（Non-local means filtering，NLMF）[4-5]将图像中噪声点的滤波过程转化为图像块之间的滤波，将图像中所有与噪声点图像块相似的图像块参与滤波，能够实现对噪声点的有效滤除。但也存在如下问题：①图像块一般设定为方形，对于诸如图像中建筑物边缘等连续性信息时，会将一些无关的像素点囊括至图像块中，导致所获取的图像块间相似度不高，无法获得较为理想的滤波效果；②图像块间的相似性主要是通过两者间的像素灰度值向量的欧氏距离来进行衡量，而对于图像中结构相似信息相似的区域，可能由于其与噪声点区域的欧氏距离较大，而被赋予较小的权重值，从而导致最终的滤波结构没有较好地顾及图像结构信息。近年来，学者们对该算法进行了一些改进，主要局限于通过将NLMF与图像分析框架如离散余弦变换简单结合[6]，或者通过对NLMF算法添加一个预滤波环节来进一步提高滤波效果[7]，总体上来说，提升幅度有限。文献[8]通过采用值聚类的方法，来实现自适应获取相似图像块，对于NLMF中的图像相似块的划分方法有了重大改进，但是聚类中心数量无法根据图像的特征自适应获取。

基于以上分析，本文尝试从相似图像块划分方法以及滤波权重值计算方法这2个方面对NLMF进行适当改进，并将其与NSCT相结合，实现对红外噪声图像滤波，引入了NAS-RIF算法[9]，来对滤波后图像视觉效果进行进一步提升。

1 红外图像NSCT变换

红外图像NSCT变换的基本思路是，采用一种类似小波基函数的多尺度分解滤波器来获取图像中边缘等细节信息的奇异点，在此基础上结合图像方向信息将捕捉到的位置相近的图像奇异点加以汇集，即采用类似于轮廓线段的结构来对图像进行刻画。红外图像NSCT变换流程如图1所示。

图1 红外图像NSCT变换

2 非局部均值滤波算法及其改进

2.1 经典非局部均值滤波算法

红外噪声图像＝{()|∈}（表示图像的坐标域）中任一噪声点的非局部均值滤波值为：

式中：(,¢)（(,¢)∈[0, 1]）为权重值，其作用在于衡量图中像素点¢与噪声点的相似程度。

若记N¢和N分别为像素点¢、所在的图像局部方形区域灰度矩阵，那么，该2点的相似程度决定于N¢和N像素程度，N¢与N¢的相似性可由两者灰度值向量的欧氏距离确定：

式中：(N)、(N¢)分别为N¢与N灰度值向量；（＞0）为高斯核函数标准差。

经过式(2)计算后，图像中灰度值矩阵间欧氏距离越小，则说明两者相似度较高，那么在滤波时赋予较大的权重值，权重值可按照下式进行计算：

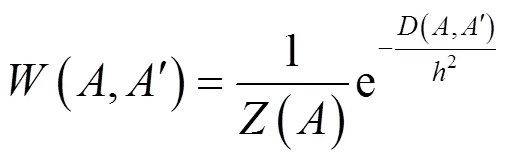
其中：

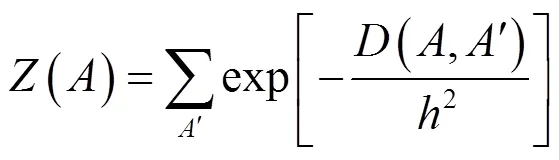
式中：为调节因子，其作用在于控制权重值(,¢)相对于(,¢)的衰减程度。

2.2 非局部均值滤波改进算法

2.2.1 自适应图像块划分方法

该方法的基本思路是，通过将图像中的像素点根据各自灰度值的接近程度，设定一定的阈值来对图像中的像素点加以区分，在某种程度上实现相似像素点的动态聚类，从而有效划分出图像中相似的图像块。如此获得图像相似块有2个特点：①不规则性，图像块的划分完全决定于像素点灰度值的接近程度，不受像素点间的距离限制，若图像中某一目标信息如河流，其划分的结果便为长条形；②自适应性，图像中不同目标信息在图像中体现为不同的灰度值分布，因而获得的图像相似块，可以随着像素点灰度值的实际分布情况，自适应地调整图像块的形状和尺寸。为了便于论述，将噪声图像的搜索区域尺寸简化为9×9，相似图像块提取具体步骤如下：

Step1：统计搜索区域内所有像素灰度均值

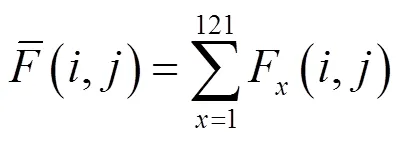
式中：F(,)为区域内任意一点灰度值。

Step3：若子区域1中，存在孤立的像素点，那么保持该类像素点不变，各自作为一个图像块存在；若存在2个或以上的像素点“聚集”区（记为子区域1¢），那么，将该类区域中像素点灰度值组成集合：

＝{1(,),2(,),3(,), …,F(,)} (＜81) (6)

式中：F(,)为区域1¢中的任一像素点灰度值。统计集合中的灰度中值：

med(,)＝Med()＝Med{1(,),2(,),

3(,), …,F(,)} (＜81) (7)

式中：Med(×)为取中值运算。将med(,)记为阈值1¢，对阈值1¢中的像素点进行进一步划分。

Step4：参照Step3对子区域2进行处理，完成对该区域内像素点的划分。

Step5：对Step3和Step4划分后的相似图像像块进行适当合并，并反复执行Step1～Step5从而完成整幅图像相似图像块的划分。

2.2.2 滤波权重值计算

经过上述划分后，图像被划分成诸多图像块，非局部均值滤波算法仅通过衡量图像块间欧氏距离的大小来作为衡量其余待滤波像素点的相近程度，如果距离较大，则相近程度较小，从而导致该部分信息在滤波过程中被较少或者不考虑，这对于细节信息丰富的红外图像而言，处滤波效果不佳。对此，通过综合考虑图像块间的结构信息以及欧氏距离，从而提出了一种新的滤波权重设定方法。结构相似度（Structural Similarity，SSIM）作为一种符合人类视觉信息敏感性的图像质量评价方法，将图像中的亮度、结构、对比度等信息进行有效结合，实现对图像质量的整体评价，图像中以像素点和¢为中心的图像块可通过下式评价两者的结构相似性：

式中：(,¢)、(,¢)、(,¢)分别表示以像素点和¢为中心的相似图像块的亮度、对比度以及结构等信息；和¢为相似图像块灰度均值；、¢为相似图像块灰度值标准差；¢为相似图像块的灰度值协方差；调节因子1,2,3计算公式为：

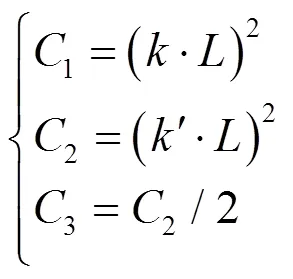
式中：,¢为调节系数（,¢∈(0,1)）；为图像灰度级，一般来说，取255。

SSIM数值越大则说明图像块的相近程度越大；而依据式(2)可知，图像块欧氏距离越大则说明两者相近程度较小。因此，设计出一种新的结构参数：

(,¢)＝1－|SSIM(,¢)|(10)

此时，图像块间相近程度越高，(,¢)越小，且(,¢)∈[0,1]其单调性与式(2)保持一致了。将式(2)与式(11)相结合，从而得到下式：

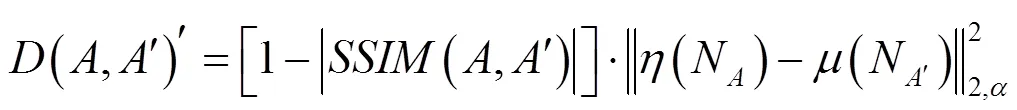
于是，将式(11)代入式(3)，可得到新的权重计算公式：

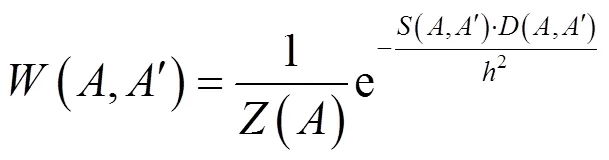
其中：

通过式(13)计算得到的相似图像块中的各像素点不仅彼此距离相近，而且结构信息相近，如此得到的相似图像块，能对图像中的细节信息进行更好地刻画。

3 非负支撑域有限递归逆滤波算法

滤波后的红外图像可抽象地表示为：

(,)＝(,)*(,)＋(,) (14)

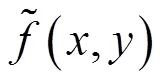
4 实验结果分析

本文首先对红外噪声图像采用NSCT域INMF算法进行处理，对于去噪后的图像采用NAS-RIF算法进行复原，在进一步抑制图像中残留噪声的同时，获得最佳视觉效果的复原图像。以MATLAB软件为实验平台，对本文算法、NLMF、以及文献[7]中的算法分别进行编程实现，并进行滤波效果横向对比分析，结果分别见图2～图3。采用峰值信噪比（PSNR）[10]和结构相似度（SSIM）[11]作为滤波后图像质量的客观性评价因子，结果见表1。

图2 原始图像与噪声图像

图3 添加入方差为10的高斯噪声图像滤波结果对比

图4 添加入方差为15的高斯噪声图像滤波结果对比

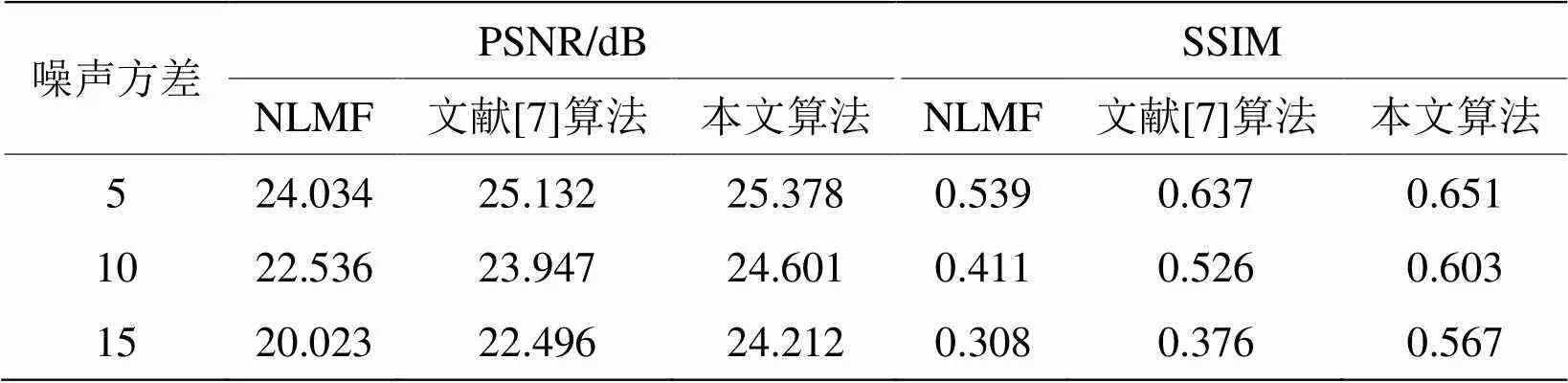
表1 文中几类算法滤波后图像质量客观评价结果

单纯采用NLMF算法对含有高斯噪声的红外图像进行滤波结果如图2(a)和图3(a)所示，可见图中比较模糊，究其原因在于：NLMF算法采用固定大小矩形窗口获取图像相似块，单纯采用相似图像块间的欧氏距离来计算滤波权重值，容易导致将与噪声点毫不相似或者说相似程度较小的噪声点参与到滤波过程中，导致滤波后图像出现了不同程度的失真。文献[7]通过将高斯滤波算法与主成分分析方法（Principal component analysis，PCA）引入到NLMF算法中，通过对图像进行预先高斯滤波，然后对滤波后图像进行PCA降维，最后进行NLMF处理，结果如图2(b)和图3(b)，相对于NLMF而言，图中模糊程度有所减轻，特别是图2(b)相对于图2(a)而言，图中左侧树杆轮廓能够依稀辨认出来。图2(c)和图3(c)为本文算法滤波结果，可以清晰地看出，图中噪声抑制程度在文中4类算法中是最佳的，这说明本文的算法的改进策略有一定的效果。

由表1可知，当图像中的高斯噪声方差逐渐增大时，文中3类算法滤波结果的PSNR值也呈下降的趋势，但下降幅度有所不同，前2类算法PSNR值下降了2.445～4.011dB，本文算法PSNR值下降了仅仅为1.166dB，这说明，本文算法具有较好的抗噪声能力，相应的SSIM值也体现了这一特点。

5 结语

针对NLMF算法存在的缺陷，分别从相似图像块和滤波权重计算方法2个方面进行了改进，提出了一种改进自适应NLMF算法，并将其与NSCT相结合，对红外图像进行滤波。针对滤波后图像不可避免存在一定程度的失真情形，引入NAS-RIF算法进行处理。红外图像测试结果表明，本文的改进算法适合于含有不同强度高斯噪声的红外图像的滤波处理。

[1] 鲍程辉, 朱康, 贺新光. 基于非下采样Contourlet系数局部特征的遥感图像融合方法[J]. 计算机科学, 2014, 41(3): 310-313.

[2] 奉俊鹏, 杨恢先, 蔡勇勇, 等. 基于非下采样Contourlet梯度方向直方图的人脸识别[J]. 计算机应用, 2014, 34(1): 158-161, 166.

[3] 丁灿, 曲长文, 杨俭. 基于贝叶斯估计的改进Contourlet变换的SAR图像滤波[J]. 数据采集与处理, 2013, 28(6): 746-754.

[4] B. K. Shreyamsha Kumar. Image denoising based on non-local means filter and its method noise thresholding[J]., 2013, 7(6): 1211-1227.

[5] Jia Wang, ChangCheng Yin. A zernike-moment-based non-local denoising filter for cryo-EM images[J]., 2013, 56(4): 384-390.

[6] 田红磊. 基于离散余弦变换的非局部均值滤波算法[J]. 科学技术与工程, 2013, 13(11): 3123-3126.

[7] 张丽果. 快速非局部均值滤波图像去噪[J]. 信号处理, 2013, 29(8): 1043-1049.

[8] 乔子良, 杜慧敏. 基于K均值聚类NL_MEANS算法的超声图像去噪[J]. 计算机工程与设计, 2013, 35(3): 939-942.

[9] 陈波, 程承旗, 郭仕德, 等. ENAS-RIF图像复原算法[J]. 红外与激光工程, 2011, 40(3): 553-558.

[10] 李俊秀, 姜三平. 基于主成分分析的图像自适应阈值去噪算法[J]. 红外技术, 2014, 36(4): 311-315.

[11] Richard Dosselmann, Xue Dongyang. A comprehensive assessment of the structural similarity index[J]., 2011, 5(1): 81-91.

Improved Non-local Means Infrared Image Filtering Algorithm Based on NSCT

HAN Hong-guang

(312088,)

Combined with nonsubsampled contourlet transform, an improved non-local means infrared image filtering algorithm is proposed. Firstly, the infrared image noise is conducted by nonsubsampled contourlet transform. Then, the similarity image block adaptive partition method and weighting calculation method are proposed so as to improve the non-local means filtering algorithm(INLMF) to deal with the high-frequency NSCT coefficients. Thirdly, the high-frequency NSCT coefficients after filtering and low-frequency NSCT coefficients are reconstructed and the denoised image is obtained. Finally, the denoised image is processed by the non-negativity and support constraints recursive inverse filtering algorithm(NAS-RIF), so the infrared image of better visual effect is obtained. The experimental results indicated that, the performance of the algorithm in this paper is superior to the already existed improved NLMF algorithm.

infrared image processing，nonsubsampled contourlet transform，non-local means filtering，non-negativity and support constraints recursive inverse filtering

TP391.41

A

1001-8891(2015)01-0034-05

2014-08-24；

2014-12-30.

韩红光（1979-）男，讲师，硕士，主要从事计算机网络和软件应用，计算机图像处理等方面的研究。Email：hanhongguangvip@126.com。