基于K-means 聚类点密度的WSNs 加权质心定位算法*

张乙竹，周礼争，唐 瑞，余 敏

(1.江西师范大学 计算机信息工程学院，江西 南昌330022;2.江西师范大学 软件学院，江西 南昌330022)

0 引 言

无线传感器网络(WSNs)［1］是由大量的传感器节点组成，通过无线通信方式形成的自组织多跳网络，广泛应用于交通、安全、军事、医疗等领域，具有很广阔的应用前景。

目前现有的定位算法根据是否需要测量节点间的距离分为基于测距(range-based)和基于非测距(range-free)两大类。基于测距技术主要有RSSI，TOA，TDOA，AOA 等。其中，RSSI 测距技术依据接收信号强度，计算出收发节点间距离，因其成本低廉、能耗低，在无线定位技术中得到广泛应用。

三边测量法是目前最容易实现的定位算法之一，它是利用三个锚节点来确定未知节点的位置，然而单次估算的坐标值无法准确反映未知节点真实位置;文献［2］中提出利用三边测量法来估计三维点云图的方法;文献［3］中提出一种聚类改进多边定位算法(MLA);文献［4］结合煤矿井下特征，提出一种自适应RSSI 三角加权质心定位算法(WCLA);文献［5］采用RSSI 进行测距并使用Zig Bee 进行定位。

由于K-means 聚类算法在处理大数据集时具有相对可伸缩和高效率特点，正好符合WSNs 环境中大量锚节点组成的数据集。据此，本文提出一种基于K-means 聚类点密度的加权质心定位算法(KCPD-WCLA)，首次对各聚类中点的密度加以考虑。理论与仿真结果均表明:改进的算法操作性强，定位误差更小。

1 三边测量定位算法原理

三边测量定位法是以已知的三个锚节点为圆心，以锚节点到未知节点距离为半径做圆，得到三个圆交点，建立方程组求解出定位结果。定位原理如图1 所示。

图1 三边定位原理Fig 1 Trilateral positioning principle

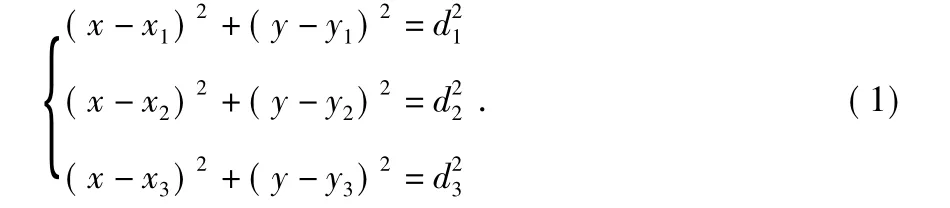
解方程组(1)即得未知节点的坐标

其中

由于受环境等因素影响，通过Shadowing 经验模型［6］得到距离存在误差，从而导致未知节点估计坐标与真实值存在一定误差，记为

2 KCPD-WCLA 设计

1)n 能被3 整除

即n%3=0(%表示取模)，得到n/3 个接近真实距离的估计位置。

2)n 不能被3 整除且余数为2

即n%3=2，因为与未知节点距离越近的锚节点在传播过程中受环境影响越小，得到距离值误差也越小，所以，选取未知节点得到的RSSI 值最大对应距离值，再与剩余的两个距离值进行分组求解，可在一定程度上减小误差。如剩余两个距离值有一个或两个都是最小距离值，则选取第二或第三小距离值计算，得［n/3］+1(［］表示取不大于n/3的最大整数)个接近真实距离的估计位置。

3)n 不能被3 整除且余数为1

即n%3=1，选取未知节点得到的RSSI 值最大对应距离值与剩余的那个距离值进行计算。如剩余距离值是最小距离值，则选取第二、三小距离值进行计算，得［n/3］+1 个接近真实距离的估计位置。

将上述结果作为K-means 聚类样本集。KCPD-WCLA设计主要经过二个步骤，步骤1 给出了K-means 聚类［7］具体过程;KCPD-WCLA 实现由步骤2 给出。

步骤1:K-means 聚类

1)数据预处理

因为基于RSSI 测距得到距离值存在误差，导致得到的聚类样本误差累积，须进行处理;否则，会严重影响后续定位算法的执行。

首先扫描一次样本集，计算每一个样本与其它样本距离，累加求其距离和，并计算距离和均值。如果某样本与其它样本距离和大于距离和均值，则将其舍弃，重复舍弃所有不合规定样本。最后得到的新数据集就是聚类初始集合。设预处理后得到的m 个聚类样本集合为M={(xi，yi)|i=1，2，…，m}。

2)K-means 聚类算法执行步骤

a.初始化:输入初始样本集合和聚类个数k。随机选择k 个样本作为k 个簇的各自中心，记为C={(cxi，cyi)|i=1，2，…，k}。

b.分配M:计算剩下的m－k 个样本到k 个聚类中心距离dij(第i 个样本到第j 个聚类中心距离)，把dij中最小的样本i 划分到聚类j。当m－k 个样本全划分到聚类，则组成k 个聚类集，记为W={wi|i=1，2，…，k}。

c.修正W:取各聚类中所有元素平均值作为新的聚类中心，重复找到所有聚类中心C'={(c'xi，c'yi) |i=1，2，…，k}。

d.判断C'是否等于C:若C'=C，则算法结束;否则，令C'=C，返回步骤b。

步骤2:KCPD-WCLA 实现

1)由步骤1 得到k 个聚类，聚类集合记为W，包括各聚类点集合及其点个数ni。

2)K-means 聚类算法具有各聚类内样本紧密度高、聚类间差异度大、得到的k 个集合包含点个数不尽相同等特点。先选择各聚类的聚类中心作为质心定位算法中多边形顶点，即把C 作为多边形顶点;当第i 个聚类wi中包含点个数ni越大，说明未知节点在wi中出现机率越大，基于此给予该聚类越大权重，则KCPD-WCLA 表达式如下

3 仿真实验与结果分析

本文采用Matlab 对提出的算法进行仿真实验，以此来验证算法的有效性。实验环境设置在200 m×200 m 的正方形区域内，未知节点布设在中心(100，100)m 处，设置参数k=5。为降低偶然性误差，在相同环境下进行50 次实验取平均值。在区域内改变布设的锚节点个数得到一系列未知节点坐标估计值，并与多边定位算法(MLA)和WCLA 进行比较。

1)算法计算复杂度分析

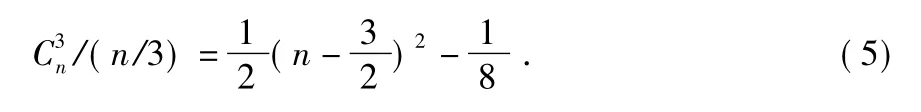
图2 计算次数比较Fig 2 Comparison of computation times

2)定位精度比较

随机布设500 个节点，锚节点数从50 个增到200 个，每次增加25 个。节点部署如图3 所示，其中正方形代表未知节点真实位置，菱形代表锚节点。仿真如图4、图5。

图3 WSNs 节点部署Fig 3 WSNs node deployment

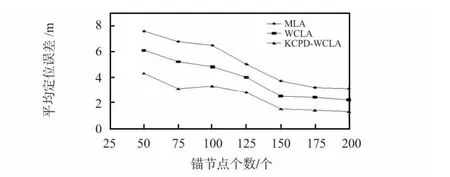
图4 平均定位误差Fig 4 Average localization error

图5 最大定位误差Fig 5 The maximum localization error

从图4、图5 可得，随着n 增加，KCPD-WCLA 平均定位误差和最大定位误差都有明显下降，平均定位误差比MLA小50.1%，比WCLA 小34.9%;最大定位误差比MLA 小46.7%，比WCLA 小27.8%，且当n=150 时，定位误差基本稳定。

4 结 论

本文在原始数据分组的基础上，采用了不重复的三个距离信息进行分组，大大降低了运算量，同时把K-means 聚类算法引入到WSNs 定位中，提出KCPD-WCLA。仿真结果表明:该算法比MLA 和WCLA 在定位精度上有明显改善，具有可操作性强，定位精度高等优势，符合WSNs 一般性应用场景，具有普遍适用性。

［1］ Rabindra Bista，Yong-Ki Kim，Jae-Woo Chang.A new approach for energy-balanced data aggregation in wireless sensor networks［C］∥Ninth International Conference on Computer and Information Technology，South Korea:IEEE，2009:9－15.

［2］ Hyun Chul Roh，Yungeun Choe，Jinyong Jung，et al.Position estimation of land-mark using 3D Point cloud and trilateration method［C］∥The 11th International Conference on Ubiquitous Robots and Ambient Intelligence，Kuala Lumpur，Malaysia:IEEE，2014:298－302.

［3］ 孙大洋，钱志鸿，韩梦飞，等.无线传感网络中多边定位的聚类分析改进算法［J］.电子学报，2014，42(8):1601－1607.

［4］ 曹开来，余 敏.无线传感器网络煤矿井下RSSI 自适应定位算法［J］.传感器与微系统，2014，33(6):129－132.

［5］ Heinemann Anna，Gavriilidis Alexandros，Sablik Thomas，et al.RSSI-based real-time indoor positioning using Zig Bee technology for security applications［C］∥The 7th International Conference on Multimedia Communications Services and Security，Krakow，Poland:IEEE，2014:83－95.

［6］ 朱明辉，张会清.基于RSSI 的室内测距模型的研究［J］.传感器与微系统，2010，29(8):19－22.

［7］ Reche Cristina，Viana Mar，Brines Mariola，et al.Determinants of aerosol lung-deposited surface area variation in an urban environment［J］.The Science of the Total Environment，2015，517(1):38－47.