基于分段信号假设检验的方差估计算法*

袁燎原，章卫国，刘 洋，刘小雄

(西北工业大学 自动化学院，陕西 西安710072)

0 引 言

加权数据融合算法根据传感器的方差分配权系数，在精度较差的传感器参与融合的情况下，依然能够提高融合精度，因此，该算法得到了广泛的应用［1～6］。而实际中传感器的测量噪声受到传输误差、环境噪声以及人为干扰等多因素影响，方差并非始终不变，不能简单等同于传感器自身方差参数或通过经验指定，需要采用算法进行实时估计。方差估计的准确与否决定了最终融合结果的精度。

典型的方差估计算法包括相关系数法［3，4］和平均值偏差法［5］。上述两种方法中所采用的移动数据窗长度固定，对测量噪声变化缺乏自适应性，无法同时保证方差变化时的快速跟踪和方差不变时的精确估计，会导致融合精度的下降。

本文在平均值偏差法的基础上，提出了一种改进算法，通过引入多元假设检验环节实现移动数据窗长度的自适应调整，提高方差估计的精度。

1 平均值偏差法

由于各待测状态量通常为解耦的，不失一般性，选取测量一维状态量的多传感器系统作为研究对象。n 只传感器对系统状态参数的量测方程为

式中 x 为一维状态量，Y=［y1y2… yn］T为n 维测量向量，e=［e1e2… en］T为n 维测量噪声向量，ei相互独立且满足为各传感器测量方差，H=［1，…，1］T。

在线性最小方差估计的准则下，加权融合估计值为

融合误差为

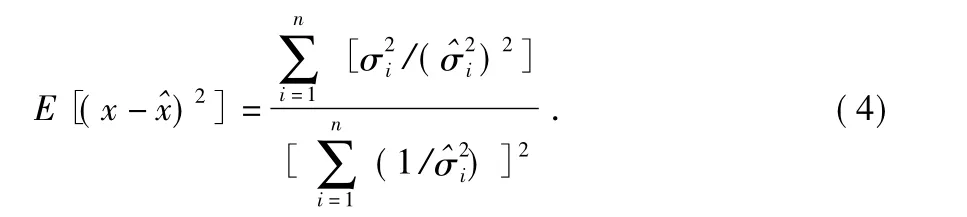
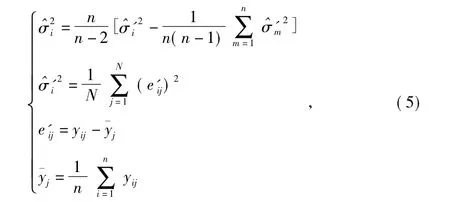
式中 yij为第i 传感器第j 次的采样值，N 为移动数据窗长度。

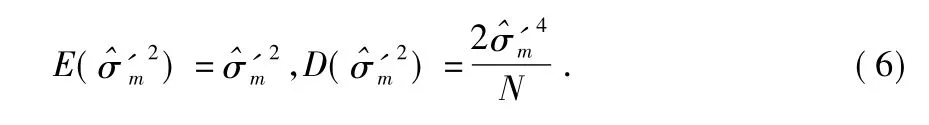
2 改进算法

基于上述分析，设计改进算法流程如图1 所示。方差估计采用自适应长度数据窗，当给出方差不变决策时，数据窗长度不断递增，从而减小方差估计误差;当给出方差变化决策时，数据窗长度从1 重新开始增加。

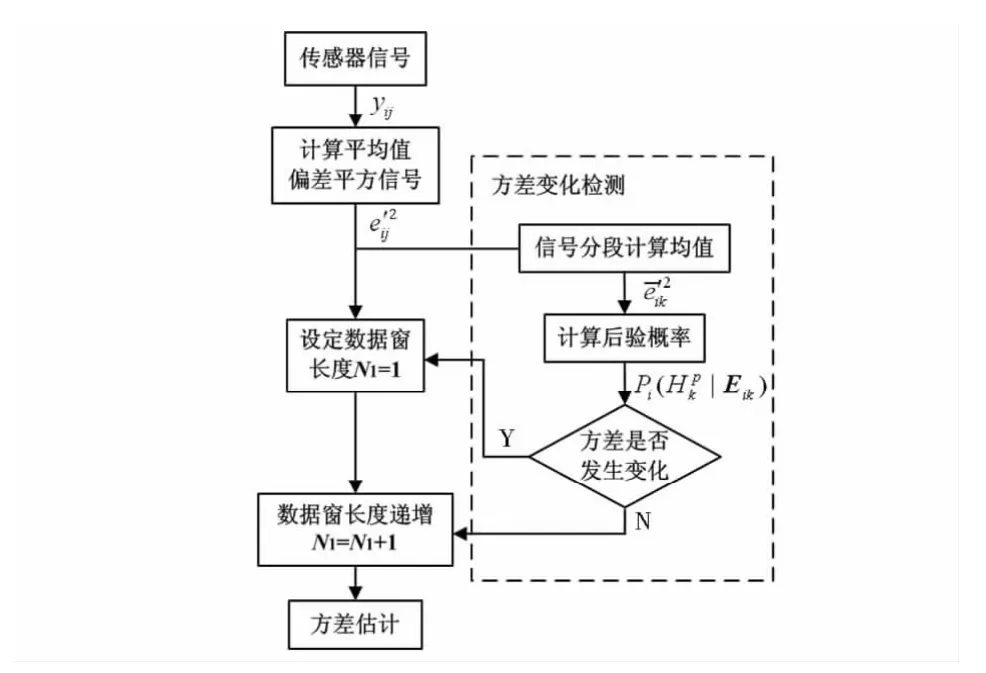
图1 改进的算法流程Fig 1 Flow chart of the improved algorithm

方差估计环节采用基于式(5)的递推形式，表达式为

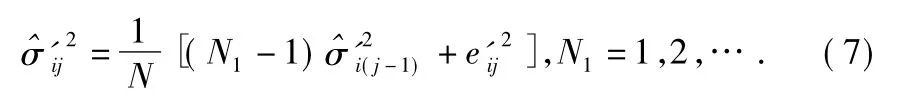
方差变化检测环节通过平均值偏差分段信号的多元假设实现，变化检测的主要作用在于及时改变数据窗长，避免N1过大导致最新采样数据影响减小，估计值滞后的问题。变化检测的具体设计如下。

2.1 信号分段处理

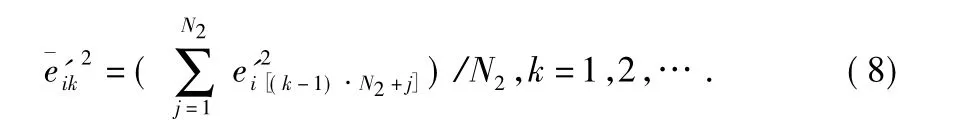
根据中心极限定理可得，当分段长度N2充分大时，信号均值逼近正态分布过程。待检测的多元假设检验为假设H0代表测量噪声方差不变，假设H1，H2分别代表方差增大和减小。

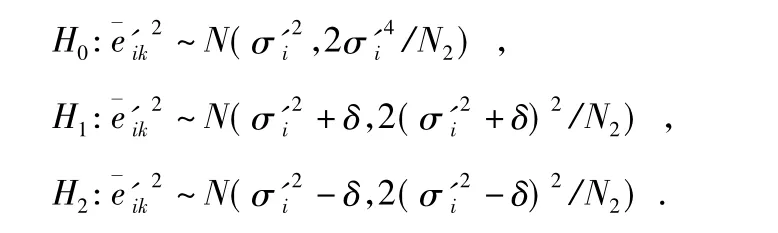
2.2 后验概率的递推计算

多元假设检验的典型判决方法为依据最大后验概率准则进行决策［8］。本文根据马尔可夫状态转移的思想，对后验概率的实时递推计算公式进行推导:

在每一采样时刻k，将假设Hp(p=0，1，2)成立，定义为一个独立的事件。3 个事件组成了马尔可夫过程的状态集合。事件、状态与假设一一对应，分析中不再作区分。

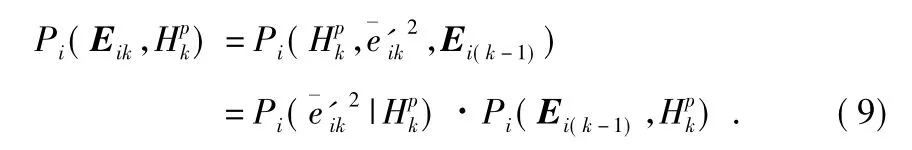
根据Ei(k－1)与以及马尔可夫状态之间的独立性，对进行推导

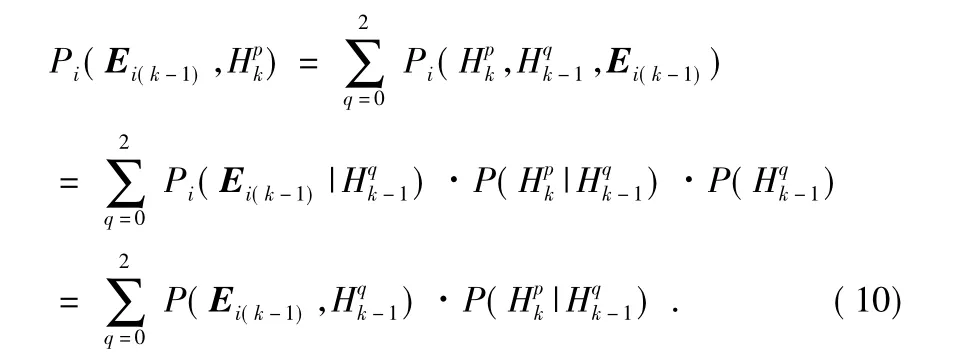
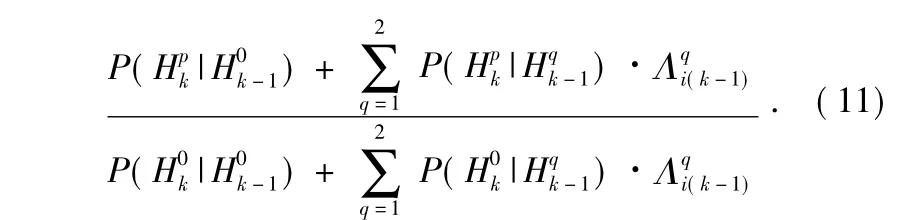
根据实际工程中的以下条件，可以对式(11)进一步化简:

基于步骤(1)～(3)，式(11)可化为

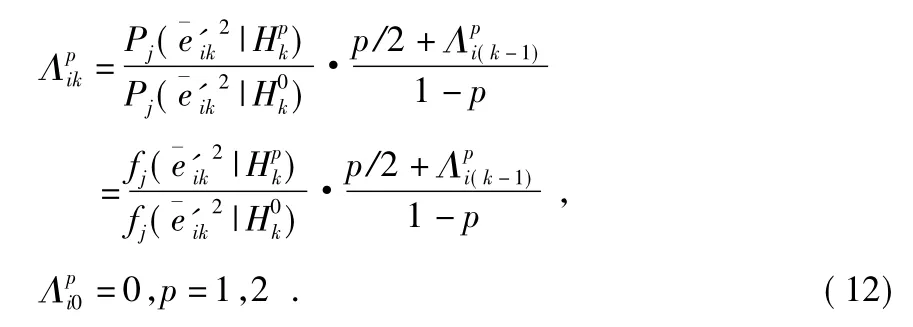
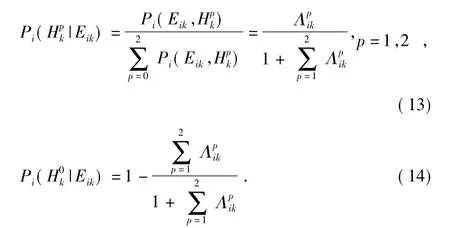
通过式(12)～式(14)即可实现后验概率的实时递推计算，从而根据最大后验概率准则进行方差变化的检测决策。

3 仿真与分析

选取四余度角位移传感器系统为仿真对象，构建测量噪声不变与变化两种仿真环境。传感器测量噪声服从正态分布，标准差分别为:0.09，0.1，0.15，0.3，采样周期T=0.02 s，仿真时间t=50 s。测量噪声变化设置为:在仿真时刻t=10 s 时，标准差变为0.17，0.2，0.26，0.11。融合精度的评价指标为均方根误差(RMSE)。

3.1 平均值偏差法的局限性

1)测量噪声稳定的情况

采用平均值偏差法对传感器1～4 以及方差相近的传感器1～3 分别进行方差估计并进行加权融合，均方根误差为RMSE1和RMSE2。方差准确已知下传感器1～4 融合结果的均方根误差为RMSE3。传感器4 的方差估计误差最大，是影响信息融合精度的主要因素，其均方根误差记为表1 给出了不同数据窗长度N1设置下，上述精度指标之间的对比。

由表1 可知，当N1设置较小时，方差估计存在较大误差，当N1＜100 时，RMSE1＞RMSE2表明传感器4 信号的引入不但未能提高融合精度，反而由于方差估计误差的影响导致传感器4 信号的权系数不够准确，使得传感器1～4 融合精度要小于传感器1～3 的融合精度。因此，为获得理想的融合效果，需要增大N1的值。

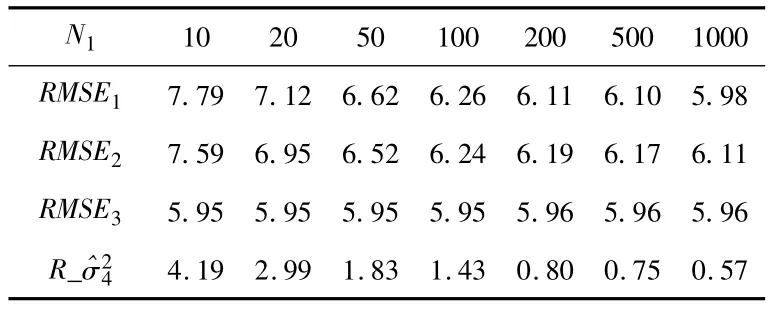
表1 数据窗长与融合误差(0.01°)间的关系Tab1 Relationship between length of data window and fusion error

2)测量噪声变化的情况

通过将参数N1设置为较大值可以有效提升测量噪声稳定时的融合精度。当N1=1000，RMSE1与RMSE3基本相等，此时方差估计误差对融合精度的影响可以忽略。

然而，测量噪声变化时，图2 所示的方差估计值跟踪灵敏度明显下降，方差估计值存在N1T 时间的滞后。在未得到稳定方差估计前，融合精度必然受到影响，具体融合精度变化曲线在3.2 小节给出。

图2 测量噪声变化时典型方法的方差估计曲线Fig 2 Variance estimation curve with typical method under noise change condition

3.2 改进方法的仿真对比

采用改进方法对传感器1～4 进行方差估计和加权数据融合。改进方法的参数设置为:信号分段长度N2=20，p=4×10－5。测量噪声稳定时，融合结果的均方根误差RMSE=0.059 7°，与方差已知时的融合精度基本相同，表明方差估计误差的影响得以消除。噪声变化时的方差估计结果如图3 所示，改进方法相对于平均值偏差法，能够更快速地实现对噪声方差变化的跟踪。

进一步比较噪声变化时两种方法加权融合精度，分别采用改进方法与典型方法进行5000 次加权融合实验，融合结果的均方根误差如图4 所示。对比均方根误差曲线可知，测量噪声稳定时，两种方法的融合精度相当;而当噪声发生变化时，改进方法的融合精度明显高于固定N1取值的典型方法。

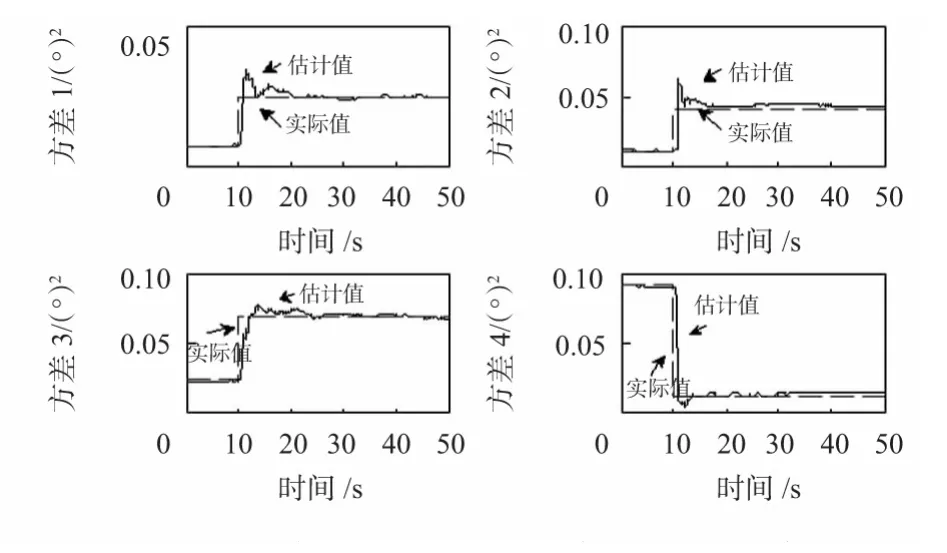
图3 测量噪声变化时改进方法的方差估计曲线Fig 3 Variance estimation curve with the improved method under noise change condition

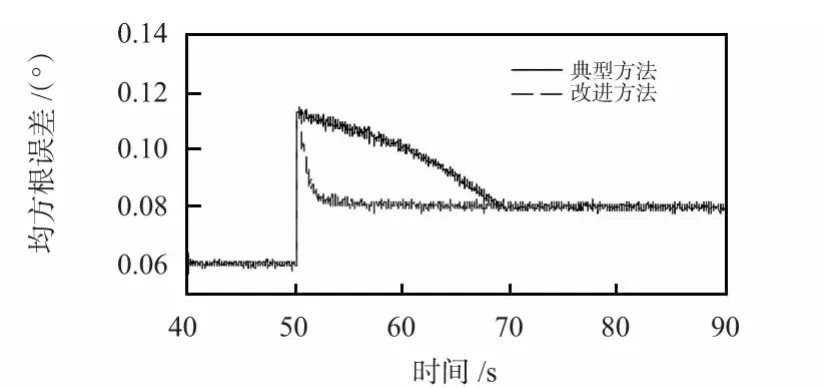
图4 两种方法的融合精度对比Fig 4 Fusion precision comparison between two methods

4 结 论

1)平均值偏差法无法兼顾测量噪声稳定时的方差估计精度和测量噪声变化时的跟踪灵敏性。参数N 设置较小，精度较差传感器信号参与加权融合不能提升融合精度;参数N 设置较大，则无法避免测量噪声变化时的融合精度下降。因而，该方法具有较大的局限性。

2)改进方法通过自适应移动数据窗和假设检验环节设计，有效克服了典型方法的上述局限，仿真结果验证了所提方法的正确性和优越性。

［1］ Khaleghi B，Khamis A，Karray F O，et al.Multi-sensor data fusion: A review of the state-of-the-art［J］.Information Fusion，2013，14(1):28－44.

［2］ 周 军，王志胜，周凤岐.基于线性均方估计的数据融合理论［J］.宇航学报，2003，24(4):364－367.

［3］ 李 伟，何鹏举，高社生.多传感器加权信息融合算法研究［J］.西北工业大学学报，2010(5):674－678.

［4］ 胡士强，张天桥.多传感器在线自适应加权融合跟踪算法［J］.北京理工大学学报，2002，22(1):117－120.

［5］ 仲崇权，董西路，张立勇，等.多传感器测量中的方差估计［J］.数据采集与处理，2004，18(4):412－417.

［6］ Gao Shesheng，Zhong Yongmin，Zhang Xueyuan，et al.Multi-sensor optimal data fusion for INS/GPS/SAR integrated navigation system［J］.Aerospace Science and Technology，2009，13:232－237.

［7］ 吴利平，李 赞，李建东，等.基于信号分段处理的截尾型序贯检验算法［J］.电子学报，2011，39(10):2412－2416.

［8］ Ray A，Phoha S.Calibration and estimation of redundant signals for real-time monitoring and control［J］.Signal Processing，2003，83(12):2593－2605.