基于重心偏移量的无人机图像兴趣点检测算法

李鹏俊，李建增

(军械工程学院 无人机工程系，河北 石家庄050050)

0 引 言

图像特征提取技术被广泛地应用于计算机视觉任务处理中，譬如:图像拼接［1］、图像检索［2］、图像配准［3］、目标识别［4］、SLAM 系统［5］等。兴趣点检测作为其中最关键的一步，一直是人们研究的热点。在过去的40 多年里，人们提出了许多兴趣点检测算法，这些算法大多都集中研究图像局部区域的不变性，包括旋转不变性、尺度不变性和仿射不变性等。对无人机图像进行深入研究发现，利用定位与方向系统(positioning and orientation system，POS)数据对图像进行简单的空间姿态校正后，可以削弱旋转、尺度及仿射等变换，进而可以将其忽略。

无人机在战场进行侦察作业时，往往会受到敌方的干扰，完成一次侦察任务往往需要多次飞行，导致拍摄的图像很容易受光照、模糊和噪声等非几何变换的影响。同时，为使图像能实时传回到地面控制站进行处理，还需要对图像进行压缩传输。这些因素的存在都大大提高了兴趣点检测的难度。为此，本文利用区域重心抗干扰能力强的特性，提出了基于重心偏移量(offset of barycenter，OoB)的兴趣点检测算法。通过与几种常用兴趣点检测算法实验对比，结果表明:本文所提算法具有较强的鲁棒性和抗干扰能力。

1 兴趣点检测

兴趣点检测是在图像大量像素点中提取出具有某种特征的点集。自1977 年，Moravec 提出利用灰度方差进行兴趣点检测以来，陆续有大量的兴趣点检测算法被提出。1988年，Harris C 等人［6］在其基础上发展出了利用自相关矩阵进行角点提取的Harris 算子，该算子提取角点速度较快，但抗干扰能力差。1994 年，文献［7］提出的Shi－Tomasi 角点检测算法对Harris 算法进行改进，提高了图像仿射变换情况下的鲁棒性。2006 年，Rosten E 等人［8］提出的FAST 角点检测算法，具有很强的实时性，但对噪声较为敏感。2008 年，Bayn H 等人［9］在SIFT 算法的基础上提出了SURF 斑点检测算法，该算法具有尺度不变性和较高的鲁棒性，但算法需要建立多尺度空间，并不适合对无人机图像的处理。

2 基于OoB 的兴趣点检测算法

文献［10］将图像看成是一块质量密度不均匀的薄板，那么，对应的图像各阶矩就有其相应的物理含义，如，零阶矩为薄板总质量，一阶矩表示薄板的重心等。受此启示，本文提出了基于OoB 的兴趣点检测算法。

2.1 区域重心

区域的矩是利用区域内所有的点计算出来的，对噪声具有较强的鲁棒性［11］。设图像的强度函数为f(x，y)，那么，可以定义图像的p+q 阶矩如式(1)

区域的重心是根据区域的零阶矩和1 阶矩计算出来，设区域的重心坐标为Δ=(Δx，Δy)，其计算公式为

2.2 算法原理

定义OoB 指的是区域的几何中心(形心)到重心之间的距离，如图1 所示。它的大小在一定程度能表征图像结构的变化，偏移量越大，变化越剧烈，相应的区域信息量越丰富。兴趣点检测总是希望其所在区域信息丰富，这样在生成特征描述符时，更具独特性。

基于OoB 的角点检测算法流程如下:

1)对无人机图像进行预处理，利用POS 系统提供的姿态数据和高度信息对图像进行空间姿态校正。

图1 检测示意图Fig 1 Detection diagram

2)设置局部区域半径，计算局部区域像素圆的0 阶和1 阶矩。为了计算的结果严格符合区域圆范围，对0 阶和1阶矩进行修正。

3)根据步骤(2)计算的0 阶和1 阶矩计算重心坐标。

4)根据重心坐标和圆心坐标计算局部区域的OoB，形成检测响应图像。

5)利用非极大值抑制的方法，在5×5 的区域内进行极大值搜索，并设置阈值t，当极大值大于所设阈值时，将其作为兴趣点。

6)对兴趣点进行定位，直接使用区域的重心坐标作为兴趣点的位置坐标。

3 实验结果

3.1 评价指标

本文给出了四项指标，对算法的性能进行对比分析，它们分别是整体复现率、单边复现率、精确度及对应点对数。

3.1.1 复现率

复现率评价指标最早由Schmid C［12］提出，“复现率为两幅图像上检测出来的一致点对数量占总观测点数的百分比”。

1)记图像Ii上检测到的兴趣点点集为{pointi}，图像Ij上的点集为{pointj}

2)实际上，对于图像Ii上一点pointi来说，很难精确地在图像Ij上检测到pointj，使之满足pointj=Hji·pointi。而只需满足pointi映射到pointj的ε 领域内，即可认为它们是一对对应点对

3)复现率定义式如下

文献［13］对以上复现率定义存在的问题与不足进行了分析，并提出了两种精确性更好的复现率评价指标:整体复现率与单边复现率。

整体复现率

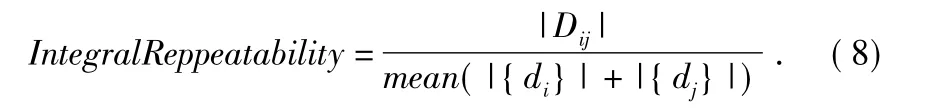
单边复现率

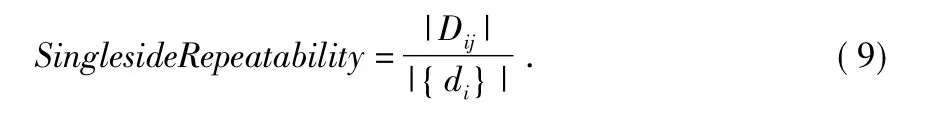
整体复现率体现了两幅图像的相似程度;单边复现率评价了兴趣点应对图像变化的鲁棒性。文献［14］分析文献［15］所用整体复现率计算方法可能导致在一些情况下计算的复现率不准确，并给出了一种新的复现率计算方法如式(10)所示

经过仔细对比，最终选用式(9)和式(10)作为复现率计算公式。

3.1.2 精确度

定义:在对应点对中，图像Ii上的兴趣点经单应变换Hji映射到图像Ij上，与Ij上对应兴趣点之间的偏差的平均水平，即

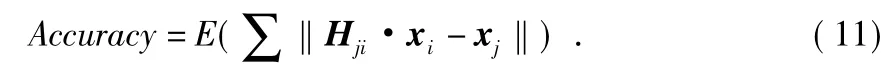
3.2 数据集

本文所用数据集如图2 所示，这些图像大多选自Mikolajczyk 提供的参考图像。

图2 数据集Fig 2 Data set

3.3 实验结果

实验对比结果如图3 ～图6 所示。

分析实验结果发现:1)不论是光照变暗、模糊增大、压缩比提高还是噪声加强，复现率都呈减小的趋势，相应的对应点对的位置误差呈增大趋势，对应点对数量呈减少的趋势;2)不论是整体复现率，还是单边复现率，OoB 算法的都要高一些。

图3 光照变化Fig 3 Illumination changes

4 结束语

图4 图像模糊Fig 4 Image blur

图5 图像(JPEG)压缩Fig 5 JPEG compression

图6 图像加噪Fig 6 Image adding noise

本文提出了一种新的无人机图像兴趣点检测算法，该算法相比其它算法来说结构简单且具有较强的抗干扰能力。通过实验，对比了光照、模糊、压缩及噪声对各兴趣点检测算法性能的影响。结果表明:1)在光照持续变暗、模糊程度变大、压缩比提高和噪声增大的情况下，各个算法的复现率和一致点对数都呈减小的趋势，而相应的误差(即精确度)呈增大的趋势;2)OoB 算法较其它几种算法的复现率要高一些，特别是能体现算法鲁棒性的单边复现率;3)OoB 算法在光照变化和噪声影响的情况下的单边复现率趋势曲线要比模糊和压缩情况下的趋势曲线变化要更加平缓，故在光照变化和噪声影响的情况下OoB 算法的抗扰动能力更强。

本文只有在获取POS 信息对无人机图像进行姿态和比例校正的基础上，OoB 算法才能获得最佳的性能，在具有重叠区域的图像上能更稳定地检测出一致对应点对。

［1］ Wu Yu，Yu Tao，Xie Donghai.Fast automatic stitching for images of unmanned aerial vehicle in emergency response［J］.Journal of Computer－Aided Design＆Computer Graphics，2013，25(3):410－416.

［2］ Schmid C，Mohr R.Local grayvalue invariants for image retrieval［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19(5):530－535.

［3］ Wang Yuru，Huang Jianhua，Liu Jiafeng，et al.An efficient imageregistration method based on probability density and global parallax［J］.Int’l J Electron Commun(AEÜ)，2010，64(12):1148－1156.

［4］ Lowe D G.Object recognition from local scale－invariant features［C］∥Proceedings of the Seventh IEEE International Conference on Computer Vision，1999.

［5］ Gil A，Mozos O M，Ballesta M，et al.A comparative evaluation of interest point detectors and local descriptors for visual SLAM［J］.Machine Vision and Applications，2010，21(6):905－920.

［6］ Harris C，Stephens M.A combined corner and edge detector［C］∥Proceedings of the 4th Alvey Vision Conference，Manchester，UK，1988:147－151.

［7］ Shi J，Tomasi C.Good features to track［C］∥Proceedings 1994 IEEE Computer Society Conference on Computer Vision and Pattern Recognition，NY，USA，1994:593－600.

［8］ Rosten E，Drummond T.Machine learning for high－speed corner detection［J］.Lecture Notes in Computer Science，2006，3951(1):430－443.

［9］ Bay H，Ess A，Tuytelaars T，et al.Speeded－up robust features(SURF)［J］.Computer Vision and Image Understanding，2008，110(3):346－359.

［10］Wei Weibo，Rui Xiaoting.Study on moment invariant method［J］.Fire Control and Command Control，2007，32(11):114－117.

［11］Zhang Yujin.Image engineering［M］.2nd ed.Beijing:Tsinghua University Press，2007.

［12］Schmid C，Mohr R，Bauckhage C.Comparing and evaluating interest points［C］∥Proceedings of the Sixth International Conference on Computer Vision，Bombay，India，1998:230－235.

［13］Smirnov P，Semenov P，Redkin A，et al.Toward accurate feature detectors performance evaluation［J］.Lecture Notes in Computer Science，2011，6962(1):51－60.

［14］Miao Zhenwei，Jiang Xudong.Interest point detection using rank order LoG filter［J］.Pattern Recognition，2013，46(11):2890－2901.

［15］Mikolajczyk K，Tuytelaars T，Schmid C，et al.A comparison of affine region detectors［J］.International Journal of Computer Vision，2005，65(1/2):43－72.