天基光学传感器姿态实时校正算法*

范 斌，邓新蒲，杨俊刚，陈 军，马 超

(国防科技大学 电子科学与工程学院，湖南 长沙410073)

0 引 言

卫星在轨运行过程中，由空间环境导致的传感器热变形、机械振动导致的平台抖动等因素使得载荷安装矩阵具有时变特性［1］，造成图像定位偏差［2，3］。为提高图像实时定位精度必须在分析载荷安装误差特性和建立误差模型的基础上，利用已知控制点对相关误差进行实时校正。

目前，在安装误差处理方案中，薛永宏等人［4］用单频正弦信号对周期失配角建模，不能拟合实际复杂的失配角变化。王炯奇等人［5］利用星敏感器测量数据滤波，估计抖动振动引起的误差，该方法假设安装误差具有稳态性，不具一般性，并且该方法利用星敏感器测量数据作为观测，不能消除载荷的安装误差。为此，本文通过对天基光学传感器成像模型与误差特性的分析，建立多频正弦信号叠加的失配角模型，采用基于特征点的天基传感器姿态实时校正方法，有效解决了天基光学传感器姿态的实时、高精度估计问题。

1 天基光学传感器成像模型与误差特性

天基光学传感器成像模型描述了目标的空间三维坐标到像平面二维坐标的投影关系，可以通过一系列的坐标系旋转变换描述［6，7］，其过程如图1 所示。

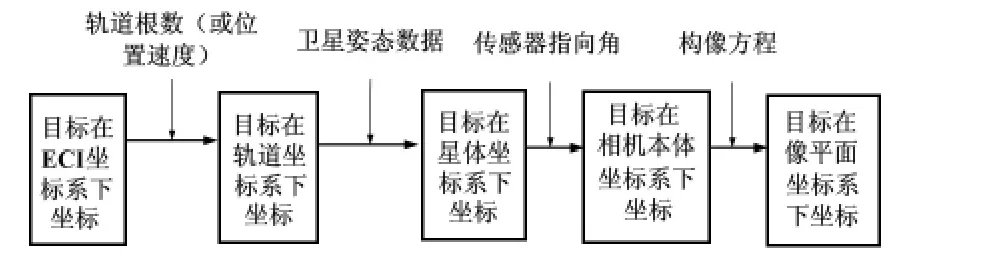
图1 天基传感器成像模型Fig 1 Space-based sensor imaging model

从物方r 到像方rpic的成像过程可以描述为

其中，rpic为恒星在像平面坐标系下的坐标，rsen为恒星在传感器坐标系下的坐标，rECI为卫星与恒星连线在地惯坐标系下的矢量，r 与rsat分别表示恒星点和卫星在地惯坐标系下的坐标，函数f(rsen)表示传感器坐标系下物方到像方的投影变换为地惯系到传感器坐标系的转换矩阵，其定义如下

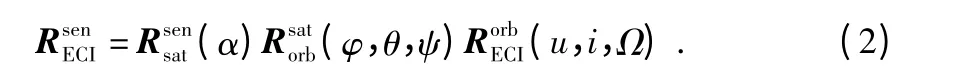
上面给出的推导是理想状况下的结果，实际成像过程要受到很多因素的干扰，实际特征点在像平面的位置与理想情况是有偏差的，其主要来源于以下两个方面:

1)观测传感器内部存在复杂的热形变、光学畸变等误差。

2)受空间热环境、机械振动等因素影响产生传感器安装形变误差。

传感器安装误差对姿态确定精度有较大影响，国内外相关文献对其特性研究［8］表明:卫星在轨飞行过程中，受太阳运动等因素对安装误差产生接近周期性的影响，这种周期性的影响通常由若干个周期性分量叠加而成。Kwork M Ong［8］在美国静止气象卫GOES 的姿态确定中提出用多个周期分量拟合安装误差的方法，实际应用中5 阶级数便能满足基本需求。

传感器的安装形变可以用卫星在滚动、俯仰、航偏三个方向的失配角(Δφ，Δθ，Δψ)描述。对模型进行必要的简化，得到姿态失配角模型如下

其中，a 为姿态失配角常值分量，c 为各周期余弦分量的幅度，ω 为周期变量的基波频率，Kwork M Ong［8］在文献中指出该量与地球绕太阳运动相关，可以认为是常量。

2 天基光学传感器姿态实时校正算法

本文采用工程应用中常用的扩展卡尔曼滤波(EKF)，实现对安装误差的实时估计。利用卡尔曼滤波估计姿态失配参数，首先需要建立状态模型和观测模型。

2.1 状态模型

参考式(4)建立的姿态失配角模型，设状态向量

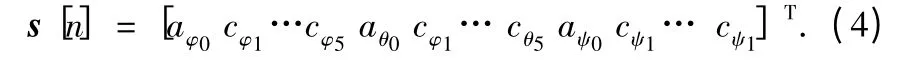
考虑实际情况中可能出现的模型失配影响，并将这种影响看作噪声输入，则状态方程可以表示为

2.2 观测模型

用卫星在滚动、俯仰、航偏三个方向的失配角(Δφ，Δθ，Δψ)描述天基光学传感器的安装误差，则成像变换矩阵表示为

在特定的条件下，卫星平台轨道根数(u，i，Ω)、姿态角(φ，θ，ψ)以及传感器指向角α 都可以通过地面或星上设备测量获得，可以视为已知量。

其中，R(Δφ，Δθ，Δψ)=Ry(Δθ)Rx(Δφ)Rz(Δψ)，在小角度近似的情况下可得

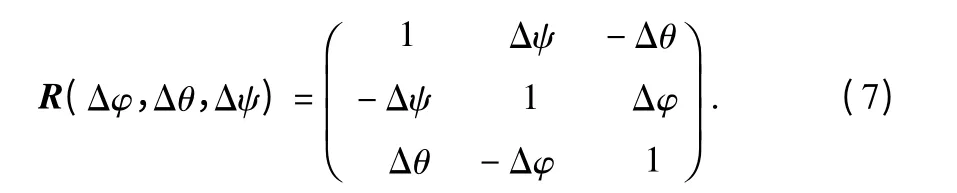
为了说明主要问题，这里暂时不考虑观测传感器构象模型的影响，则观测模型可以表示为

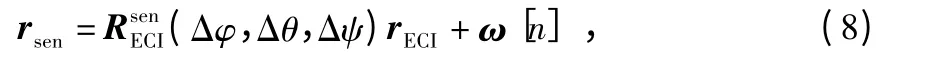
定义rECI=［rx，ry，rz］T，首先(Δφ，Δθ，Δψ)rECI对向量(Δφ，Δθ，Δψ)求导得

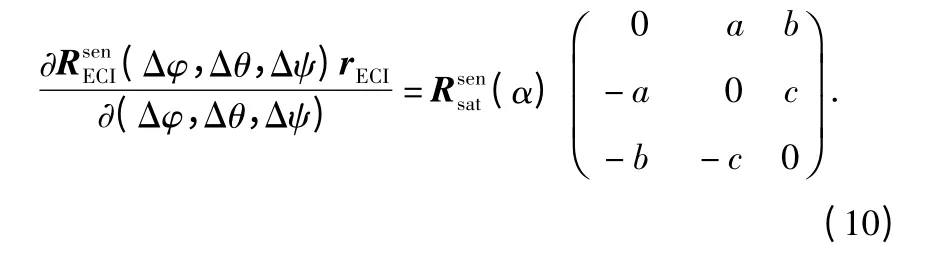
其中

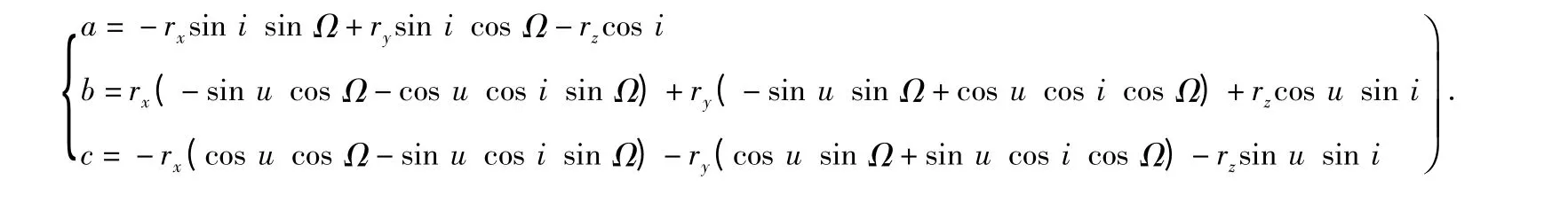
其次，(Δφ，Δθ，Δψ)对状态向量s［n］求导得

2.3 算法实现

算法的实现流程如图2。

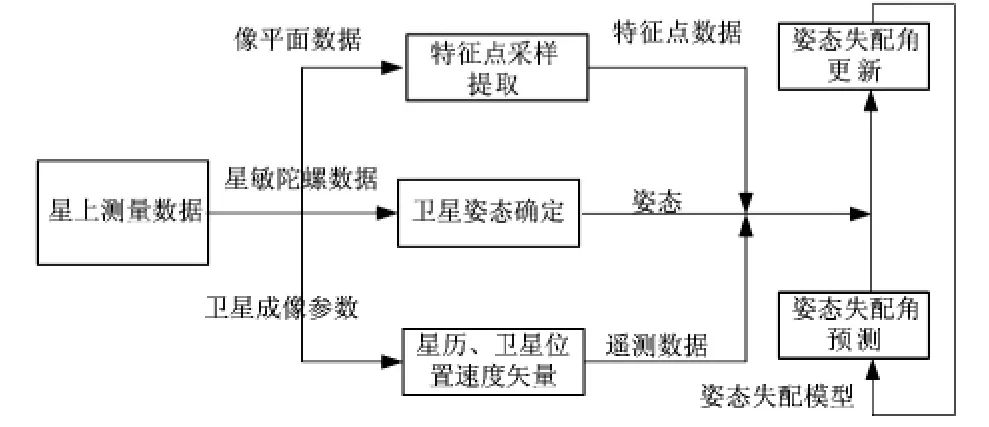
图2 天基光学传感器姿态实时校正原理图Fig 2 Real-time attitude calibration principle of space-based optical sensor

2.3.1 预测

设^表示估计值。在tn－1时刻，利用状态模型对状态矢量进行预测，预测计算为，同时利用M［n|n－1］=AM［n－1|n－1］AT+Q 得到误差协方差矩阵。其中，A 为状态转移矩阵，Q 为驱动噪声阵。

2.3.2 更 新

若在tn时刻的观测图像中检测出了特征点，则利用该测量rsen，n对预测的状态矢量及其协方差矩阵进行更新

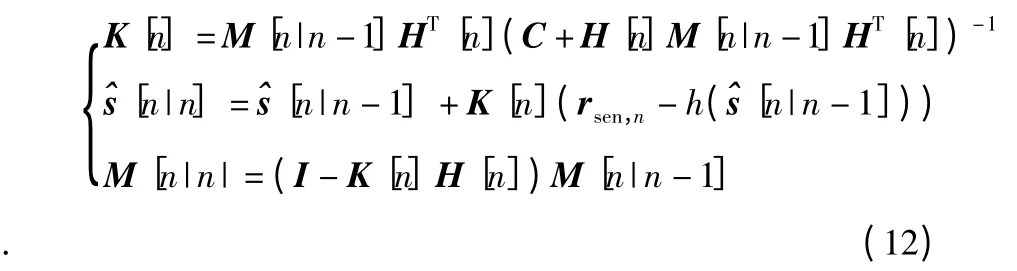
若在tn时刻的观测图像中未检测出恒星特征点，则利用当前时刻的预测值作为状态矢量与协方差矩阵的更新值

经过滤波得到每一时刻的状态矢量，代入式(4)得到实时的安装误差(Δφ，Δθ，Δψ)。

3 仿真实验与分析

卫星在轨运行过程中，天区可见恒星是进行图像定位的重要特征点，把这些特征点作为本仿真实验的观测。

3.1 恒星观测仿真

用STK 仿真一颗运行于地球同步轨道的GEO 卫星，卫星轨道历元时间为2015—03—01，12︰00︰00，仿真开始时间为2015—03—01，12︰00︰00，仿 真 结 束 时 间 为2015—03—02，12︰00︰00。仿真中假设卫星轨道位置误差为0.5 km，速度误差为0.1 km/s，姿态确定精度为5″。

模拟成像过程，得到21600 幅图像序列，选择每一帧图像的10 颗恒星为特征点，10 颗恒星为检验点。

3.2 安装误差影响的仿真验证

图3、图4 表明利用本文算法能够实现对安装误差的有效估计。为了进一步验证算法效果，利用滤波得到的误差参数对姿态进行校正，再利用校正后的姿态参数对恒星检验点进行检验，校正效果统计结果如表1、表2。

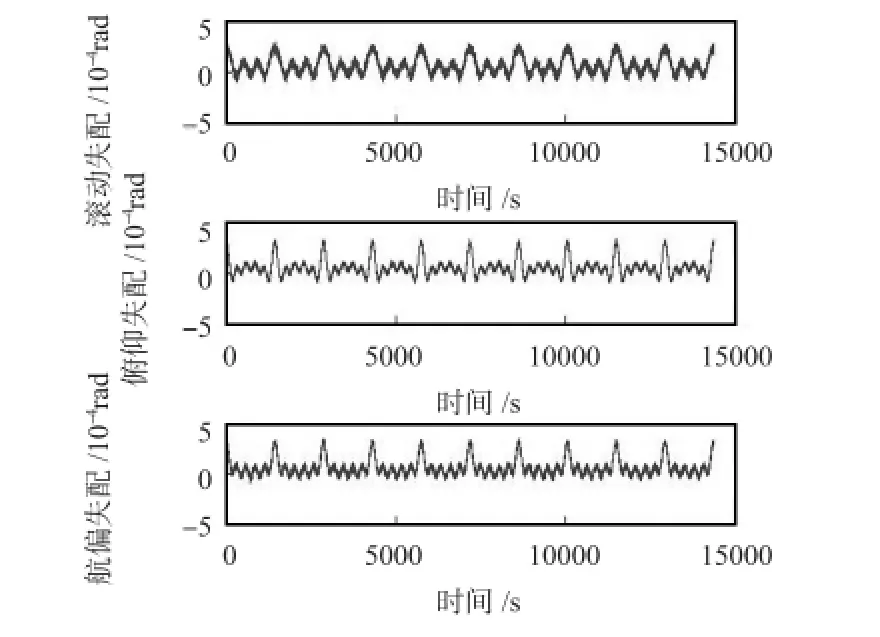
图3 真实安装误差信号Fig 3 Real installation error signal

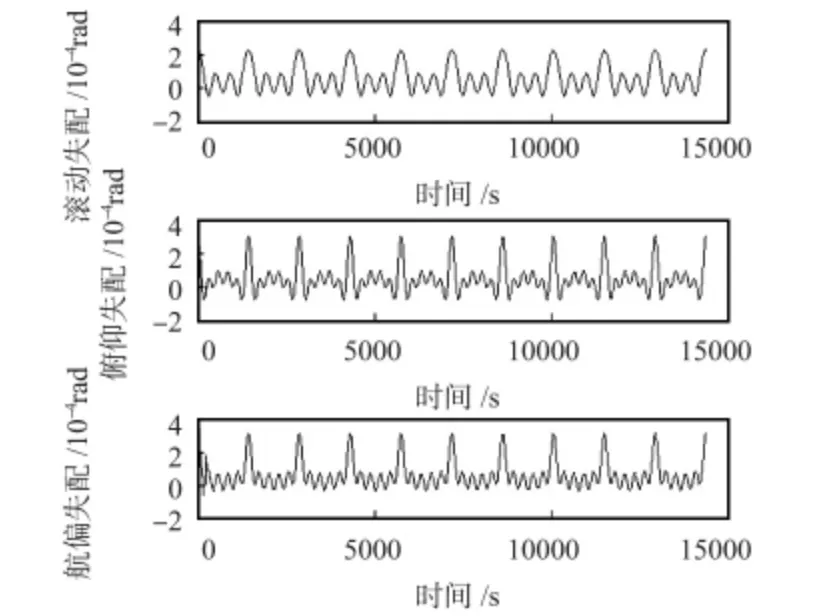
图4 卡尔曼滤波恢复结果Fig 4 Kalman filtering recovery results

表1 存在安装误差影响下的像元位置偏差Tab 1 Pixel position deviation under influence of installation error

表2 安装误差求解后像元位置偏差Tab 2 Pixel position deviation after installation error solved

对比表1、表2 的统计结果可知，经过姿态校正，图像定位偏差的最大值、最小值以及均值都有了较大程度的减小，定位精度有了较大程度的提高。

4 结束语

受载荷安装误差的影响，载荷姿态与理想状况存在较大误差，导致图像定位精度下降。本文在高精度卫星定位技术指标的要求下，分析了天基光学传感器的测量误差源，对天基光学传感器安装误差进行建模，利用恒星特征点作为观测，采用EKF 对模型参数进行实时估计。仿真结果表明:本文采用的天基光学传感器姿态校正算法能实时有效消除载荷安装误差，提高图像的定位精度。

［1］ Clemons T M，Chang K C.Sensor calibration using in-situcelestial observations to estimate bias in space-based missile tracking［J］.IEEE Trans AES，2012，48(2):1403－1427.

［2］ Andreas N S.Space-based infrared system(SBIRS)system of systems［C］∥Proceedings of IEEE Aerospace Conference，Snowmass at Aspen，CO，1997:429－438.

［3］ Wu Andy.SBIRS high payload LOS attitude determination and calibration［C］∥IEEE Aerospace Conference，Snowmass at Aspen，1998:243－253.

［4］ Xue Yonghong，An Wei，Zhang Tao，et al.Real-time line of sight calibration algorithm for high earth orbit infrared scanning sensor［J］.Acta Optica Sinica 2013，33(6):0628003.

［5］ Wang Jiongqi，Jiao Yuanyuan，Zhou Haiyin，et al.Star sensor attitude measuring data processing technique in condition of complex satellite dithering［J］.Journal of Electronic＆Information Technology，2010，32(8):1885－1891.

［6］ Sheng Weidong，Long Yunli，Zhou Yiyu.Analysis of target location accuracy in space-based optical sensor network［J］.Acta Optical Sinica，2011，31(2):129－135.

［7］ Yu Chunfeng，Ding Yalin，Hui Shouwen，et al.Analysis of image rotation for aerial remote sensor with three-mirror reflective optical system［J］.Acta Optica Sinica，2011，31(8):0823002.

［8］ Ong Kwok M，Lutz Steve.GOES orbit and attitude determinationtheory，implementation，and recent results［C］∥SPIE Proceedings，Denver，CO，US，1996:652－663.