改进的猴群算法在传感器优化布置中的应用

杜国璋，马 丽

(1.兰州交通大学 机电工程学院，甘肃 兰州730070;2.兰州交通大学 自动化与电气工程学院，甘肃 兰州730070)

0 引 言

纸纱复合袋糊底机是实现纸纱复合袋糊底的先进机器，工艺流程复杂，机构众多，主要由涂胶机构、压痕机构、折边机构等十个机构组成［1］。涂胶机构是糊底机的重要组成部分，其工作状态的好坏直接影响到产品质量的优劣，对其结构健康状况进行监测是保证产品质量的关键。

结构健康监测是指利用现场的、无损的、实时的方式采集结构与环境信息，分析结构反映的各种特征，获取结构因环境因素、损伤或退化而造成的改变［2］。对糊底机涂胶机构而言，就是如何对传感器进行优化布置，利用最少数量和最优位置的传感器获得能够反映其结构健康状况的最全面和最有价值的信息，是一类典型的组合优化问题。

传感器优化布置方法很多，如有效独立法、运动能量法、模型缩减法等传统优化算法，猴群算法(monkeys algorithm，MA)、遗传算法(genetic algorithm，GA)、粒子群优化算法(particle swarm opimization，POS)等智能优化算法。智能优化算法能较好地解决组合优化问题［3］。

MA 是一种模仿猴群爬山过程中爬、望、跳等动作实现最优解搜索的智能优化算法，2008，由Zhao Ruiqing 和Tang Wansheng 首次提出［4］。该算法参数设置较少、寻优能力强，适合求解多变量、多峰值等复杂函数的优化问题，已经在传感器优化布置、入侵检测技术、输电网扩展规划等领域得到应用，并取得了良好的效果［5］。

本文在简易猴群算法(simple monkeys algorithm，SMA)的基础上提出了一种改进的MA，以解决涂胶机构健康监测信号采集过程中的传感器优化布置问题，并通过算例对改进的算法进行了验证。

1 传感器优化布置问题分析

1.1 涂胶机构算例模型

涂胶机构主要由胶槽、印胶辊、匀胶辊、粘胶辊和转动齿轮等机构组成，工作时粘胶辊匀速转动将胶槽内的胶液涂抹于自身，同时匀胶辊反向转动，将粘胶辊上的胶液转移到印胶辊上，并进一步均匀分布，最后印胶辊将胶液均匀地涂在纸纱复合袋底部，配合其他工序，实现糊底功能。涂胶机构尺寸为860 mm×500 mm×580 mm，支撑板材料采用45#钢，弹性模量为2.0×105MPa，泊松比为0.3;辊子材料采用灰铸铁，弹性模量为1.2×105MPa，泊松比为0.25，总质量为167.25 kg。将用SolidWorks 2012 软件建立的三维实体模型导入ANSYS 15.0 进行有限元分析计算和模态分析。涂胶机构辊子采用PIPE16 单元，支撑板、底座及其他构件采用BEAM4 单元，共划分为42 041 个节点，14 469 个单元，有限元模型如图1 所示。

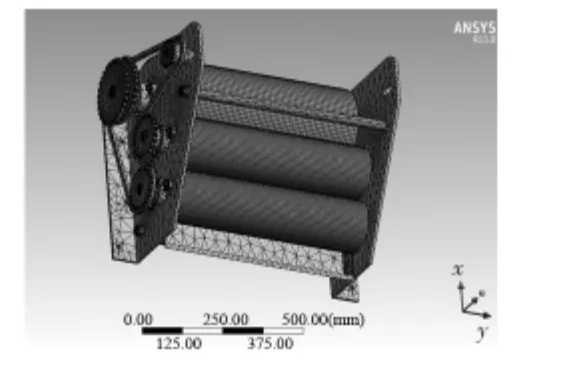
图1 涂胶机构有限元模型Fig 1 Finite element model of gelatinize agency

根据糊底机整体设计要求，印胶辊转速为21.8 r/min，匀胶辊和粘胶辊转速为32.2 r/min，其传输功率都为0.67 kW。根据扭矩公式

其中，P 为功率，kW;T 为扭矩，N·m;n 为转速，r/min。由式(1)可算出印胶辊、匀胶辊、粘胶辊的扭矩分别为T印=198.72 N·m，T粘=293.51 N·m，由于匀胶辊与印胶辊和粘胶辊的转向相反，故T匀=－293.51 N·m。给涂胶机构施加扭矩和重力加速度载荷，以底板安装固定部位为整个模型的边界条件，对有限元模型进行模态分析，得到前10 阶模态固有频率，如表1 所示。

表1 涂胶机构前10 阶模态频率Tab 1 The first 10 order modal frequency of gelatinize agency

1.2 涂胶机构传感器优化布置数学模型

测点选择问题就是满足一定准则或目标的优化问题［6］。文献［7］认为MAC 是评价模态向量空间交角的有效工具，其表达式为

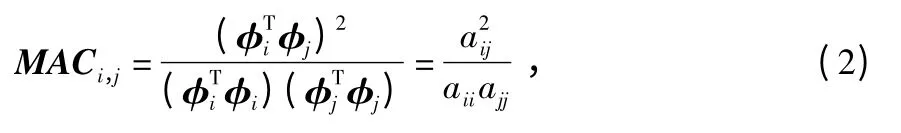
式中 φi和φj分别为振型向量矩阵Φ 中的第i 阶和第j 阶模态向量。矩阵中非对角元MACij(i≠j)能够反映两模态向量之间的交角，其值越小，传感器布置效果越好;反之，则越差。因此，测点的布置可采用MAC 的非对角元最小为目标函数，其表达式为

2 改进的MA 传感器优化布置方法

伊廷华等人提出的SMA 在传感器优化布置应用中取得了较好的预期效果［8］。但也存在以下问题，采用随机方式初始化猴群位置，不能充分实现初始猴群的均匀分布，降低了猴群的多样性，可能导致算法全局搜索能力降低［2］;采用固定的爬步长，在迭代前期不利于猴子快速找到局部最优解，而在迭代后期大步地爬行可能使猴子跳过局部最优解，不利于提高求解精度［5］。

本文针对SMA 存在的问题，通过改进初始化方法和爬步长，提出了一种用于传感器优化布置的改进MA。

2.1 编码方式与变量初始化

2.1.1 整数编码

文献［3］采用整数编码的方式进行解的表达，解决了MA 不能直接求解组合优化问题的缺陷。本文结合应用实际，采用整数编码方式解决编码问题。

对涂胶机构有限元模型采用数值求解方法提取振型数据，以含有振型数据的点为需要布置传感器的待选测点，设其数目为m，按照1 ～m 进行整数编号，得到模态振型矩阵Φm×l，l 为模态振型的阶数。

2.1.2 正态分布初始化

文献［9］认为符合正态分布的初始化种群具有多样性。每只猴子xi的各个分量xi1，xi2，xi3，…，xin服从数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)，其表达式为

式中 期望值μ 决定了每只猴子xi分布的位置，标准差σ决定了分布的幅度。

设猴群的规模为M，通过正态分布初始化第i 只猴子的当前位置，用向量表示为xi=［xi1，xi2，xi3，…，xin］T，i=1，2，…，M，n 为需要布置传感器的数目。xi中各分量的值互不相同，每个分量值表示待布置传感器的位置编号，则每只猴子的当前位置对应于一个候选的优化布置方案，f(xi)即以xi中所确定的编号位置测点的振型矩阵计算其最大MAC 非对角元的值。

2.2 爬过程

爬过程是MA 中寻找局部最优的主要过程，占用搜索时间较多。爬次数Nc和爬步长a 是影响整个算法运行速度和求解精度的重要参数，Nc越大，a 越小，求解精度越高，但收敛速度会随之降低。因此，合理设置爬过程的相关参数尤为重要［5］。

针对基本MA 采用固定爬步长不利于提高求解精度和收敛速度的问题，为了寻求二者之间的平衡，在合理确定爬次数的前提下，设置了自适应的变步长，即在爬过程的前期采用较大的步长进行搜索，加速向局部最优解靠近;随着爬次数的增加猴子逐渐接近最优解，适当缩小爬行步长，使其小步慢爬，更精确地确定最优解。设计爬步长为

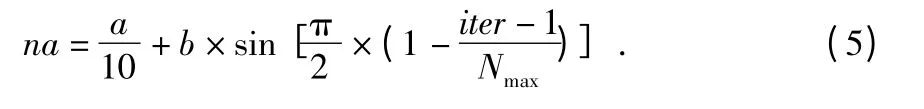
其中，a 为爬过程的初始步长，b 为望过程视野的长度，iter 为猴群的当前进化代数，Nmax为算法最大迭代次数。由式(5)可以看出，随着爬动次数的增加，爬动步长非线性地递减，逐步收缩到一个较小的值a/10。改进后爬过程的步骤如下:

1)计算本次爬步长na;

2)从区间［－na，na］中随机产生整数Δxij，组成向量Δxi=(Δxi1，Δxi2，…Δxin)T;

3)得到新位置xi+Δxi，计算f(xi+Δ xi)，若f(xi+Δ xi)＜f(xi)，则猴子的位置为xi=xi+Δ xi;否则，该猴子的位置不变;

4)重复步骤(1)，(2)，(3)，直至达到爬过程循环次数Nc为止。

2.3 望过程［2］

望过程主要通过猴子瞭望搜索附近区域比当前位置更好的解来加快搜索过程，得到局部更优解，设b 为望过程的视野长度，对于第i 只猴子其望过程的步骤如下:

1)在区间［xij－b，xij+b］，j=1，2，…，n，内随机产生猴子新位置x'i

2)计算f(x'i)，若f(x'i)＜f(xi)，则猴子的位置为xi=x'i;否则，该猴子的位置不变;

3)重复步骤(1)和(2)，直至达到望过程循环次数Nw为止。

2.4 跳过程［3］

跳过程通过猴子跳出当前区域到其他区域进行解的搜索，以增强算法的局部搜索能力，避免陷入局部最优解。设置参数λ∈［0，1］，则跳过程的步骤如下:

3 改进MA 的传感器优化布置

3.1 改进MA 步骤

1)确定算法的各项参数，根据式(4)初始化猴群位置;

2)根据式(2)计算猴群的目标函数值;

3)根据式(5)计算爬过程每次迭代的爬步长，进行爬过程局部搜索;

4)让每只猴子按照爬、望、跳的顺序不断进行最优解的搜索，直至达到最大循环次数;

5)确定MAC 矩阵最大非对角元最小时的布置点为最优解。

3.2 算例结果对比分析

由于涂胶机构比较复杂，有限元模型的自由度达到4 万多个，为提高收敛速度，减少计算时间，结合工作实际和结构特点，选取支撑底座为固定约束，以辊子的轴承座在支撑板上的安装位置和5 个转动齿轮作为传感器待布置位置，对模型进行简化，简化后的模型如图2 所示。

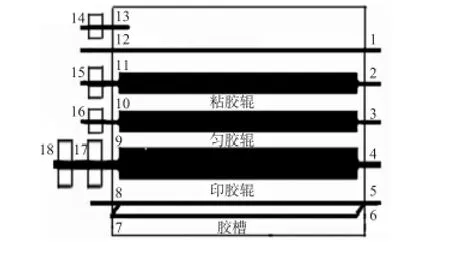
图2 涂胶机构简化模型Fig 2 Simplified model for gelatinize agency

简化模型共计18 个测点，每个测点有6 个节点自由度(平动x，y，z，转动Ux，Uy，Uz)，共计108 个自由度。选择竖向模态为目标模态，根据所得数据构造模态振型矩阵Φ108×10，利用MatlabR2009b 对改进的MA 进行编程求解。

根据工程实际和试验经验，设置参数如下:猴群规模M为50，算法最大迭代次数Nmax为50，初始爬步长a 为0.5，爬次数Nc为100，望过程视野长度b 为0.5，望次数Nw为10，数学期望μ 为1，方差σ2为6.2，λ 是在［0，1］内的随机数。依据上述参数运行程序，为提高效率，在108 个节点自由度中选取3 的倍数个自由度作为传感器待布置点，使目标函数值最优。所得MAC 值的变化曲线如图3 所示。

由图3 可知，节点自由度在10 ～15 之间时MAC 值处于最小阶段，当节点自由度为12 时MAC 值最小为0.121 9，而后MAC 值逐渐增大且有一定幅度的波动。因此，对涂胶机构布置12 只传感器比较合理。图4 是布置12 只传感器时，改进MA 与SMA 收敛曲线的对比。

图3 MAC 值变化曲线Fig 3 Variation curve of MAC value

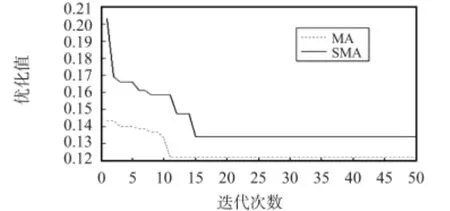
图4 改进MA 与SMA 收敛对比曲线图Fig 4 Curve of convergence comparison between improved MA and SMA

由图4 可以看出:改进的MA 在迭代12 次左右已经搜寻到最优解，而SMA 在迭代15 次时才搜索到最优解，改进的MA 收敛速度明显加快。同时，改进的MA 在迭代12 次以后优化值保持在0.122 6，SMA 在迭代15 次以后优化值保持在0.135 1，收敛精度提高了10.2%。

总之，改进的MA 与SMA 相比，搜索能力明显增强，不易陷入局部最优，收敛速度也同时加快。从节约成本、节省时间和提高效率方面考虑，将改进的MA 应用在涂胶机构的传感器的优化布置中具有一定的现实意义。传感器布置方案如表2 所示。

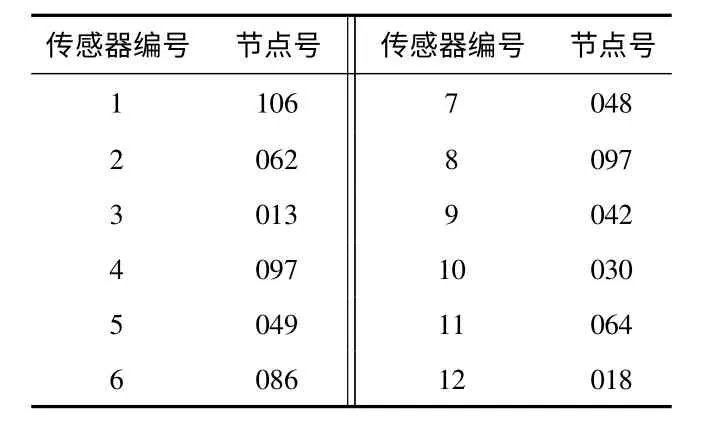
表2 传感器布置方案Tab 2 Scheme of sensor placement

表2 所得传感器布置位置大多在涂胶机构的辊子与支撑板的交点处，可以有效获取涂胶机构的健康状况信息。

4 结 论

本文提出了一种改进的MA 传感器优化布置方法，该算法以SMA 为基础，将正态分布应用到猴群的初始化当中，增强了猴群的多样性，在爬过程中采用非线性变化的自适应爬步长，提高了算法的搜索精度和收敛速度。以涂胶机构简化模型的模态分析结果为依据，用改进的MA 对其传感器布置的数量和测点位置进行优化。结果表明:与SMA 相比，改进的MA 收敛速度快、精度高、寻优能力强。

［1］ 王义兵，彭珍瑞，殷 红，等.纸纱复合袋糊底机控制系统设计［J］.制造业自动化，2015，37(1):123－126.

［2］ 伊廷华，张旭东，李宏男.基于免疫猴群算法的传感器优化布置方法研究［J］.计算力学学报，2014，31(2):174－179.

［3］ 彭珍瑞，赵 宇，殷 红，等.基于混沌猴群算法的传感器优化布置［J］.传感器与微系统，2014，33(10):104－107.

［4］ Zhao Ruiqing，Tang Wansheng.Monkey algorithm for global numerical optimization［J］.Journal of Uncertain System，2008，2(3):164－175.

［5］ 张亚洁.猴群算法及其应用研究［D］.西安:西安电子科技大学，2014.

［6］ 魏秀业，潘宏侠，黄晋英.齿轮箱传感器优化布置研究［J］.兵工学报，2010，31(11):1508－1513.

［7］ Came T G，Dohmann C R.A modal test design strategy for modal correlation［C］∥Procedings of the 3th International Modal Analysis Conference，Schenectady，Union College，New York，USA，1995.

［8］ Yi T H，Li H N，Zhang X D.A modified monkey algorithm for optimal sensor placement in structural health monitoring［J］.Smart Materials and Structure，2012，21(10):1－9.

［9］ Mehrabian A R，Lucas C.A novel numerical optimization algorithm inspired from weed colonization［J］.Ecological Informatics，2006，1(4):355－366.