基于传感器丢包率不确定性预测的分布式H∞滤波算法*

林 楠，史苇杭，魏 斌

(1.郑州大学 软件技术学院，河南 郑州450002;2.郑州大学 计算机科学与技术学院，河南 郑州450002)

0 引 言

近年来，越来越多的科学家对传感器网络的分布式滤波问题进行了研究［1，2］。分布式滤波中，传感器通过拓扑网络连接，且可以接收其自身感测的数据并通过互联网传输信息。因此，如何处理传感器之间的复杂耦合关系成为设计分布式滤波器的最重要的问题之一［3，4］。H∞滤波方法与其它滤波器相比提供了一个最坏情况下的估计误差界限，并且不需要噪声统计知识，因此，被广泛地应用到实际工程中，并成为控制领域的一个研究热点。

传感器网络的通信介质的可靠性受到外部环境的影响，并且数据包丢失在期望上的统计量很难获取［5，6］。因此，需要在传感器网络分布式估计中对数据包丢失的不确定性进行分析，无论是本地传感器还是相邻传感器的数据包丢失。

在分布式H∞滤波的研究上，吴博等人［7］通过使用稳态Kalman 滤波器对多个传感器节点的输出信号进行滤波，提出一种带滤波的无线传感器网络(WSNs)的H∞控制算法。冯肖亮等人［8］利用测量值扩维的方法，提出基于多传感器的序贯式融合有限域H∞滤波方法。李秀英等人［9］通过定义新的变量，将原系统转化为随机参数系统，提出一种具有一步随机时滞和多丢包的网络系统H∞滤波器设计方法。Dong Hongli 等人［10］提出一种有损传感器网络Markov跳跃非线性时滞系统的分布式H∞滤波器。Jiang Bin 等人［11］通过分析与设计全阶H∞滤波器，提出基于网络控制系统的T-S 模糊模型法的滤波器设计方案。

1 问题建模

采用Hn来表示n 维的欧氏空间，用Hn×k来表示所有n×k矩阵的集合。用x 表示随机向量，用‖x‖表示向量x的欧几里得范数，用I 表示单位矩阵［12，3］。E(x)，E(x|y)分别为随机变量x 的期望和在条件y 下x 的期望。

x(t)为状态向量，z(t)为被估计的信号，线性离散时间系统的表达如下

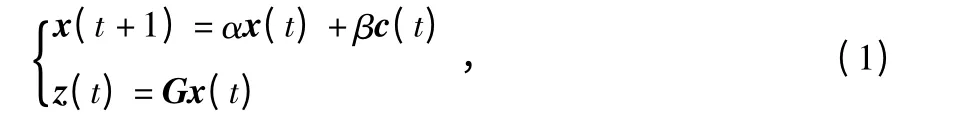
式中 c(t)为外界干扰输入，而m 只传感器服从随机数据包丢失的情况如下

式中 ys(t)为通过传感器s 接收到的来自线性离散时间系统的测量输出。As(t)为伯努利分布随机变量。

假设有N 个传感器节点分布在空间并通过一个固定的拓扑结构的无线网络进行连接。传感器网络通过一个有向图G={V，E}进行表示，V=(v1，…，vN)表示传感器网络节点集合，E=(e1，…，em)表示链路集合。来自节点vj的信息有以下基于状态跟踪的形式来接收随机丢包

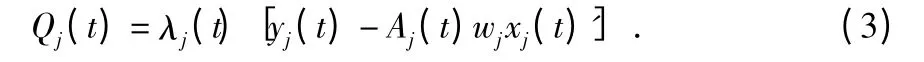
其中，xj(t)'为在传感器vj的xj(t)估算值。λj(t)为Aj(t)伯努利分布的独立随机变量，它代表着传感器之间的分组传输。

代入式(2)～式(3)中得到

为了使分析更加方便，引入另一个符合伯努利分布的随机参数Si(t)，定义

可以结合这两个独立的进程为一个，得到

根据实际环境的复杂性，讨论不确定预期的丢包率。如果Sj(t)=1，则Ai(t)=λi(t)=1。可以得到

Si(t)的数学期望可以被描述如下

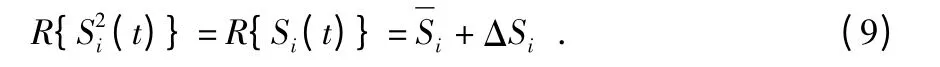
本文中，假设R{Si(t)}的不确定性是范数有界的，0≤|Si|≤γi≤1，定义，得到

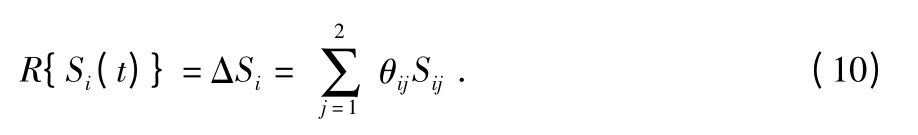
因此，通过传感器i 所接收到的信息可以用线性离散时间系统表示为

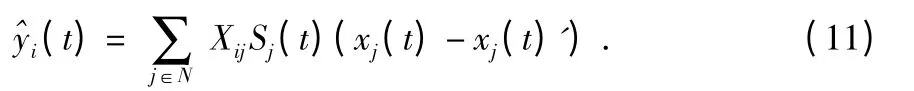
接着，在传感器i 上采用滤波器

滤波器的初始值是xi(0)'=0，i=1，2，…，N。

将式(8)代入式(9)可得

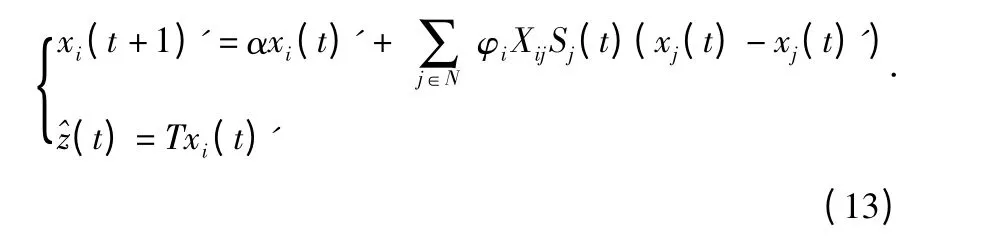
令估计误差和滤波误差分别为

对于节点i 可以得到管理滤波误差的线性离散时间系统

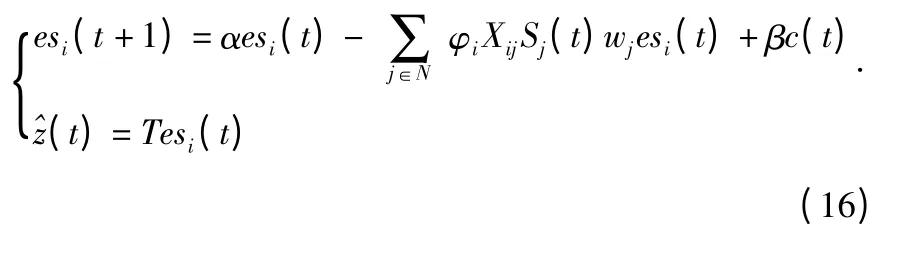
2 分布式H∞滤波

在本节中，在均方意义上对于离散时间系统的随机稳定性问题，采用一个丢包的不确定数学期望来进行讨论。通过采用参数依赖Lyapunov 泛函的方法和随机分析技术来获取可验证性条件，最终目的是找到最佳的滤波器参数φi。

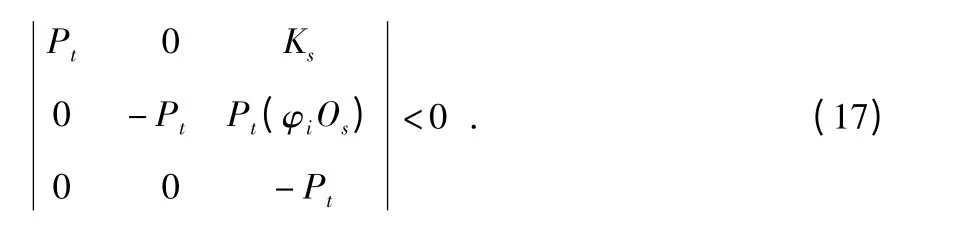
其中

最后可以得到滤波器参数φi为

3 算例分析

假设有一个线性离散时间系统，如下所示

传感器网络的拓扑结构通过一个节点集合为V=(1，2，3)，链路集合为E={(1，1)，(1，2)，(2，2)，(2，3)，(3，3)}的有向图G={V，E，L}表示，邻接矩阵L 表示为

传感器节点的动态性用参数描述为w1=［0，－0.2］，w1=［0.1，－0.2］，w1=［0.2，0.4］。

表1 对于不同的Si 况下γi 和φi 取值Tab 1 Value of γi and φi with different

表1 对于不同的Si 况下γi 和φi 取值Tab 1 Value of γi and φi with different

图1 给出了在相同情况下，通过200 次Monte—Carlo 测试本文滤波器和文献［10］的Markov 跳跃非线性时滞系统的分布式H∞滤波器、文献［11］的T-S 模糊模型法的滤波器的比较结果。

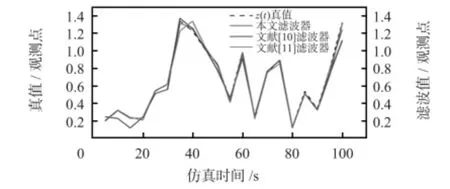
图1 真值与滤波值的对比情况Fig 1 Comparison of true value and filtering value

从图1 的对比结果可以看出:本文所提出的估计算法的滤波精度高于文献［10，11］的滤波算法，其中，文献［10］的滤波算法与真值的偏差较大，而本文算法的滤波曲线贴近于真值的曲线。由此可见，在网络环境下，即当观测数据存在不确定性丢包时，本文滤波算法更加有效。

对滤波器进行了100 次的蒙特—卡罗仿真，得到了估计值与实际值之间的误差。如图2 所示，随着仿真步数的增长，三种滤波器的误差值呈现不稳定的变化，本文滤波器的误差在(0.005 4，0.015 4)包之间，文献［10］滤波器在(0.007 8，0.017 2)包之间，文献［11］滤波器的误差在(0.009 4，0.018 9)包之间。由于信号干扰导致测量值的丢失，估算值与实际值往往存在着偏差，本文正是基于测量数据不确定丢失的问题进行了建模，并通过最佳的滤波器参数来减少估算误差。从数值上可以看出:本文滤波器的绝对误差估计比另外两种滤波器更加有效。

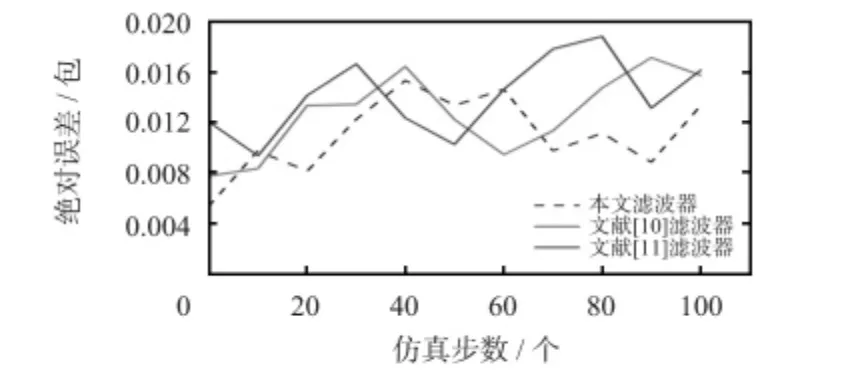
图2 绝对误差估计Fig 2 Absolute error estimation

为了进一步地分析网络不确定性因素对滤波误差动态系统稳定性的影响。在图2 的基础上，增加了网络延时、数据丢包因素，设置网络每发送一次数据延迟0.05 ms，数据丢包率为7.3%，在这种网络状态下算法滤波的误差值。从图3 中的结果可以看出:本文算法的滤波误差值的变化范围在(0.006 1，0.016 2)包之间，相比图2 中的情况，受到网络状态变化后的误差值有少许增加。文献［10］的变化范围为(0.009 2，0.018 4)包，受到网络状态影响时误差值的变化最大。文献［11］的变化范围为(0.010 5，0.018 6)，在网络状态刚发生变化时，误差值增大，之后最大的误差值不超过之前的0.018 9，但从曲线的总体分布情况来看仍高于本文提出的分布式H∞滤波算法。

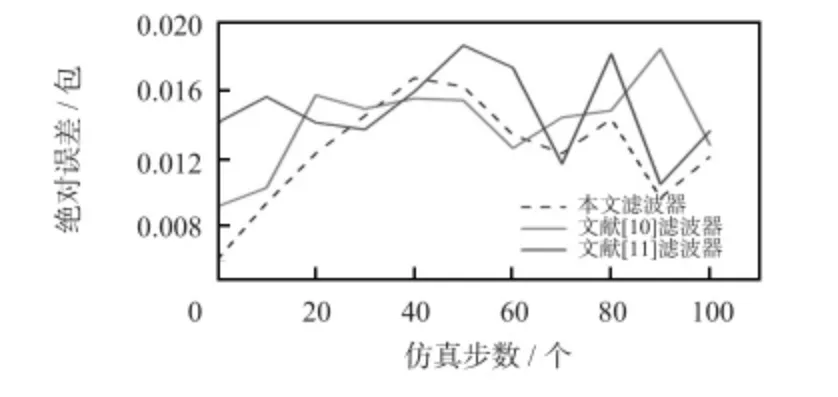
图3 在其他网络状态下的绝对误差Fig 3 Absolute error value in other network status

4 结 论

本文提出一种基于传感器丢包率不确定性预测的分布式H∞滤波算法，通过管理滤波误差的线性离散时间系统，在均方意义上对于离散时间系统的随机稳定性问题进行了讨论，并且采用参数依赖Lyapunov 泛函的方法和随机分析技术来获取可验证性条件，通过找到最佳的滤波器参数来最终实现H∞滤波的稳定性和精确性。在实验中通过与Markov跳跃非线性时滞系统的分布式H∞滤波器和T-S 模糊模型法的滤波器进行对比，体现出本文滤波算法的有效性。

［1］ Qin F，Dai X，Mitchell J E.Effective-SNR estimation for wireless sensor networks using Kalman filter［J］.Ad Hoc Networks，2013，11(3):944－958.

［2］ Demigha O，Hidouci W K，Ahmed T.On energy efficiency in collaborative target tracking in wireless sensor networks:A review［J］.Communications Surveys ＆ Tutorials，IEEE，2013，15(3):1210－1222.

［3］ Solouk V，Taghizadeh H，Akbari-Moghanjoughi A，et al.Tracking moving targets in wireless sensor networks using extended diffusion strategies of distributed Kalman filter［C］∥2013 IEEE Malaysia International Conference on Communications(MICC)，IEEE，2013:213－216.

［4］ Benini A，Mancini A，Longhi S.An IMU/UWB/vision-based extended kalman filter for Mini-UAV localization in indoor environment using 802.15.4a wireless sensor networks［J］.Journal of Intelligent＆Robotic Systems，2013，70(1－4):461－476.

［5］ Weeraddana D M，Walgama K S，Kulasekere E C.Dempster-Shafer information filtering in multi-modality wireless sensor networks［J］.World Academy of Science，Engineering and Technology，2013，79:644－651.

［6］ Torfs T，Sterken T，Brebels S，et al.Low power wireless sensor networks for building monitoring［J］.Sensors Journal，IEEE，2013，13(3):909－915.

［7］ 吴 博，关治洪，詹习生.带滤波的无线传感器网络的H1 控制［J］.控制理论与应用，2013，30(2):261－265.

［8］ 冯肖亮，文成林，刘伟峰，等.基于多传感器的序贯式融合有限域H∞滤波方法［J］.自动化学报，2013，39(9):1524－1532.

［9］ 李秀英，王金玉，孙书利.具有一步随机时滞和多丢包的网络系统H∞滤波器设计［J］.自动化学报，2014，40(1):155－160.

［10］Dong H，Wang Z，Gao H.Distributed H∞filtering for a class of Markovian jump nonlinear time-delay systems over lossy sensor networks［J］.IEEE Transactions on Industrial Electronics，2013，60(10):4665－4672.

［11］Jiang B，Mao Z，Shi P.Filter design for a class of networked control systems via T-S fuzzy-model approach［J］.IEEE Transactions on Fuzzy Systems，2010，18(1):201－208.

［12］Ma J，Sun S L.Information fusion estimators for systems with multiple sensors of different packet dropout rates［J］.In formation Fusion，2011，12(3):213－222.

［13］Sun Y G，Qin S Y.Stability and stabilization of networked control systems with bounded packet dropout［J］.Acta Auto matica Sinica，2011，37(1):113－118.

［14］Gao H，Li Z，Agarwal R.New result on H∞filtering for time-delay Markovian jump systems［C］∥2013 IEEE International Symposium on Industrial Electronics(ISIE)，IEEE，2013:1－6.