内凹面触觉传感器设计与接触过程分析*

吕根波，李成刚，申景金

(1.南京航空航天大学 机电学院，江苏 南京210016;2.南京邮电大学 自动化学院，江苏 南京210016)

0 引 言

微创手术(minimally invasive surgery，MIS)凭借其疼痛轻、创口小、术后感染风险低等诸多优点逐渐得到学者们关注与青睐。但MIS 也面临着一些挑战，如微创机器人手术中，由于医生不能直接接触患者身体，导致重要的触觉反馈信息缺失，这可能会导致健康软组织遭器械破坏，进而造成严重的医疗后果，解决该问题理想的方法是发展医用触觉传感器。

当前，国内外大量文献所提出的医用触觉传感器主要用于检测医疗器械与软组织之间的接触力，避免健康组织受到器械的破坏［1，2］。如，Tanimoto M 等人运用MEMS 技术制作了一种触觉传感器。传感器被安装在导管的顶端，结合电阻应变计，能够测量导管与血管壁间的接触力。这为病人接受介入导管治疗提供了更可靠安全的保障［3］。近几年，逐渐发展了一批能够测量软组织间相对硬度的触觉传感器，通过对软组织硬度检测，可以判断是否存在病变的组织［4，5］。

本文所设计的触觉传感器带有圆锥形内凹面，通过分析传感器上施加的载荷及其法向位移和变形软组织与传感器内凹面的接触半径之间的关系，建立接触模型，结合硬件与软件，即可实现传感器判别材料相对硬度，分析接触力，输出材料参数等特殊功能。

1 触觉传感器的描述

1.1 传感器结构

传感器结构如图1 所示，其几何形状类似于圆柱体，内部为圆锥形凹面，敏感元件均匀分布在凹面上。由于它能够反映出传感器与软组织材料间的时间接触过程，所以，通过分析敏感元件的输出信号，结合接触模型，传感器功能即可实现。

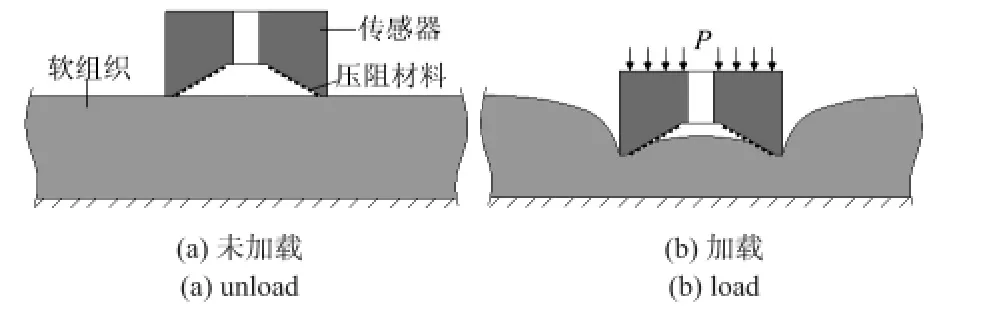
图1 传感器与组织接触Fig 1 Contact between sensor and tissue

1.2 传感器工作原理

传感器工作原理如图2。在传感器的顶端施加载荷P，则传感器内凹面下的软组织便会隆起类似驼峰的形状;在固定载荷作用下，“驼峰”的高度随时间缓慢上升，最终达到一个稳定的位置。在此过程中，传感器内壁分布的力敏元件依次受到变形组织的压力作用。变形量越大，则传感器中受到变形软组织压力作用的敏感元件数量就越多，对应的接触内径ai越小。通过电桥电路判断各个敏感元件是否受到压力作用，从而预测ai;将相关参数代入到所建立的接触模型当中，计算得到软组织的相关材料参数，辨别待测物体间的相对硬度，同时辨识组织。

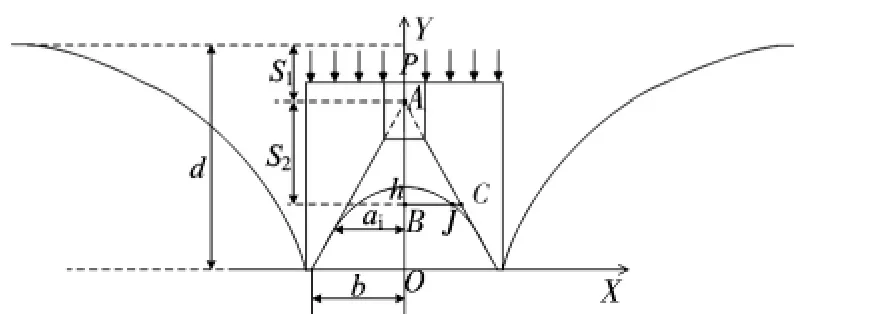
图2 传感器工作原理示意图Fig 2 Working principle of sensor

2 传感器与软组织材料间的接触模型

为获得材料属性参数，需要建立传感器顶端载荷P 与该载荷所引起软组织的变形之间的关系式。由于传感器的硬度远远大于软组织，因此，将其视为刚体。根据弹性固体和粘弹性固体对应原理，先求弹性接触解，再求粘弹性接触解。

2.1 弹性体接触模型

由图2 知，接触模型包含五个参数:ai，b，P，d 和h，分别代表接触内径，传感器底端半径，顶端载荷，竖直方向位移和内凹面圆锥高度。

首先，将变形组织任一点的位移u(r)表示成如下形式

如图2 中变形组织J 点沿Y 轴负方向的位移为s1+s2。其中，s1=d－h，s2=h(LBC/b)，此处的LBC为点B，C 之间平行于X 轴的长度，其意义同式(1)中的r。

其次，根据Collins 和Barber 提出的关于载荷P 的公式［6，7］可以推导出

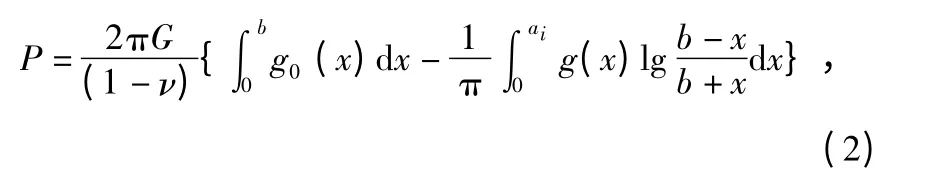
式中 ν，G 分别代表泊松比和剪切模量，x 为积分变量，其中

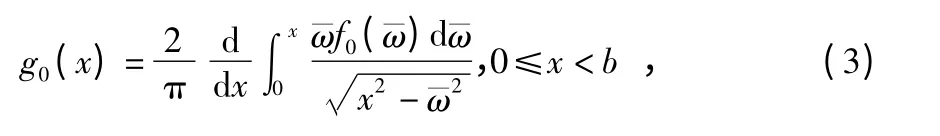
式中 g(x)为Fredholm 方程的解，该方程为

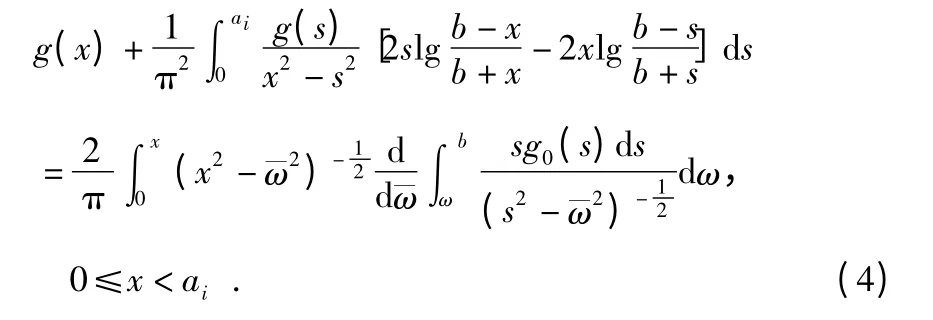
式中 λ=ai/b，该解仅在λ 较小的时候成立。将得到的g(x)代入式(2)中，则得与λ 有关的载荷函数P1(λ)

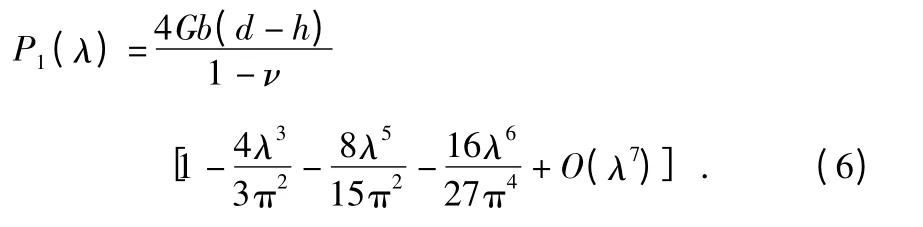
将函数u(r)的第二部分h(r/b)代入式(3)中，同样的解法求得载荷函数P2(λ)

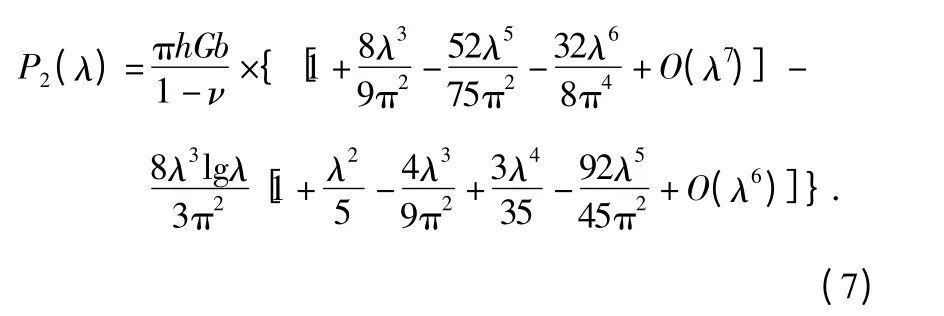
所以，式(6)、式(7)相加便可得到总载荷函数为

最后根据Barber 给出的边界条件∂P/∂λ 求得未知参数d［9］

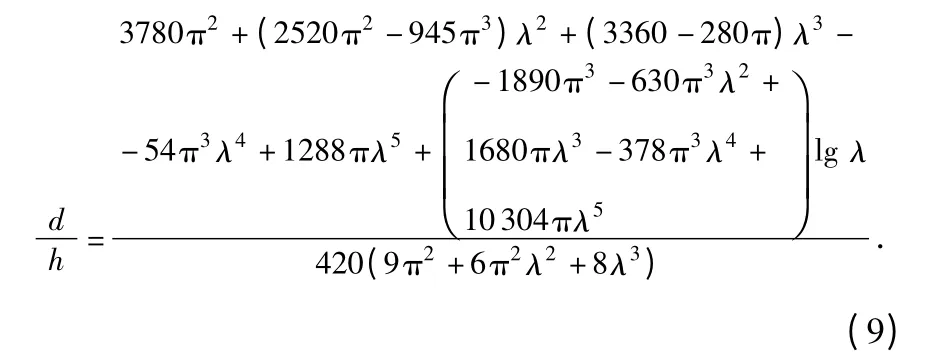
但是，当λ 趋向于1 的时候，以上所有的解便失效了。此时，通过Grinberg 和Kuritsyn 提出的方法对式(8)进行修正得［8］

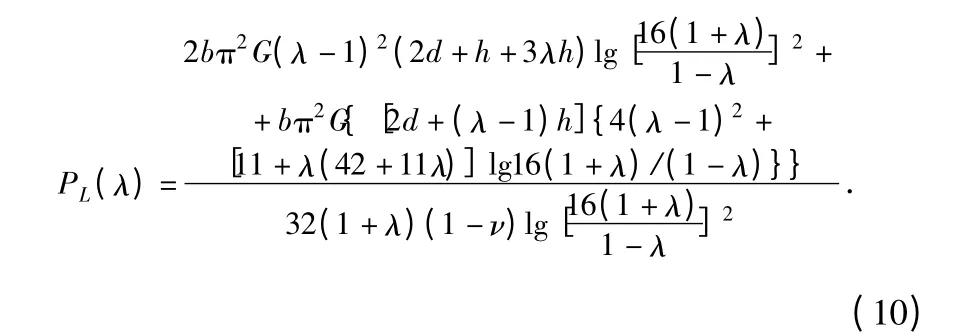
根据相应的边界条件，同样求得d

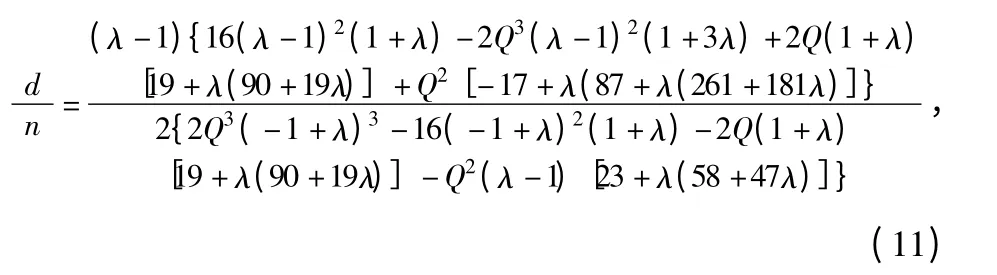
式中 Q=lg［16(1+λ)/(1－λ)］。

从而可以得到载荷P 与λ 相关的两个函数式(8)、式(10)。为了分别得出符合该两式的λ 值范围，给出传感器外壳尺寸和待测弹性体一些参数:b=2.5 mm，arctan(h/b)=15°，G1=1.765 5 MPa，G2=2.915 3 MPa，G3=4.599 2 MPa。将这些参数分别代入式(8)和式(10)中，得到结果如图3。

由图3 可知P(λ)和PL(λ)有一个共同的交点(λ=0.4149)，并且该点值不随剪切模量的变化而变化。图3 表明剪切模量越大，若要组织变形程度达到相同的λ 值，则所需要的载荷就越大。同时，当λ 趋于1 的时候(此时传感器顶端未加载荷)，P(λ)的值并不为0，而PL(λ)等于0。引起这个问题的原因主要是在λ 趋于1 时，式(5)并不是方程(4)的正确解，方程(4)的迭代解只有在λ 非常小的情况下才适用。此时，PL(λ)才是其正确的对应函数。因此，将λ=0.4149作为两个函数的分界点做进一步研究。当λ 处于(0，0.414 9)时，采用P(λ)，当λ 在［0.414 9，1］采用。

除了考虑剪切模量对两函数分界点的影响，同时还需要考虑传感器结构尺寸是否对该值有所影响。参数arctan(h/b)与传感器的锥度有关。取arctan(h/b)=15°，30°，45°以及G1=1.765 5 MPa 进行分析。同样的方法可以求得相应的曲线如图4 所示。

可见传感器外壳尺寸与软组织剪切模量对P-λ 曲线的影响类似，两函数的交点相同。P(λ)和PL(λ)的分界点λ=0.414 9进一步得到证实。此结论将会被应用到下述讨论中。

2.2 软组织材料的粘弹性模型建立

由于实际的粘弹性固体往往包含着数个到数十个松弛或蠕变过程，所以，将采用多个经典Kelvin 模型和一个弹性单元相互串联的形式来描述粘弹性固体。其广义模型示意图如图5 所示［9］。

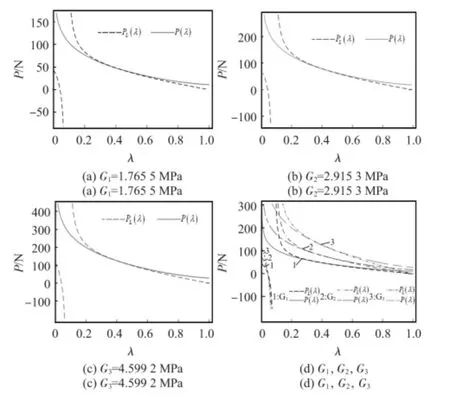
图3 不同剪切模量下P-λ 曲线图Fig 3 P-λ curves with different sheer modulus

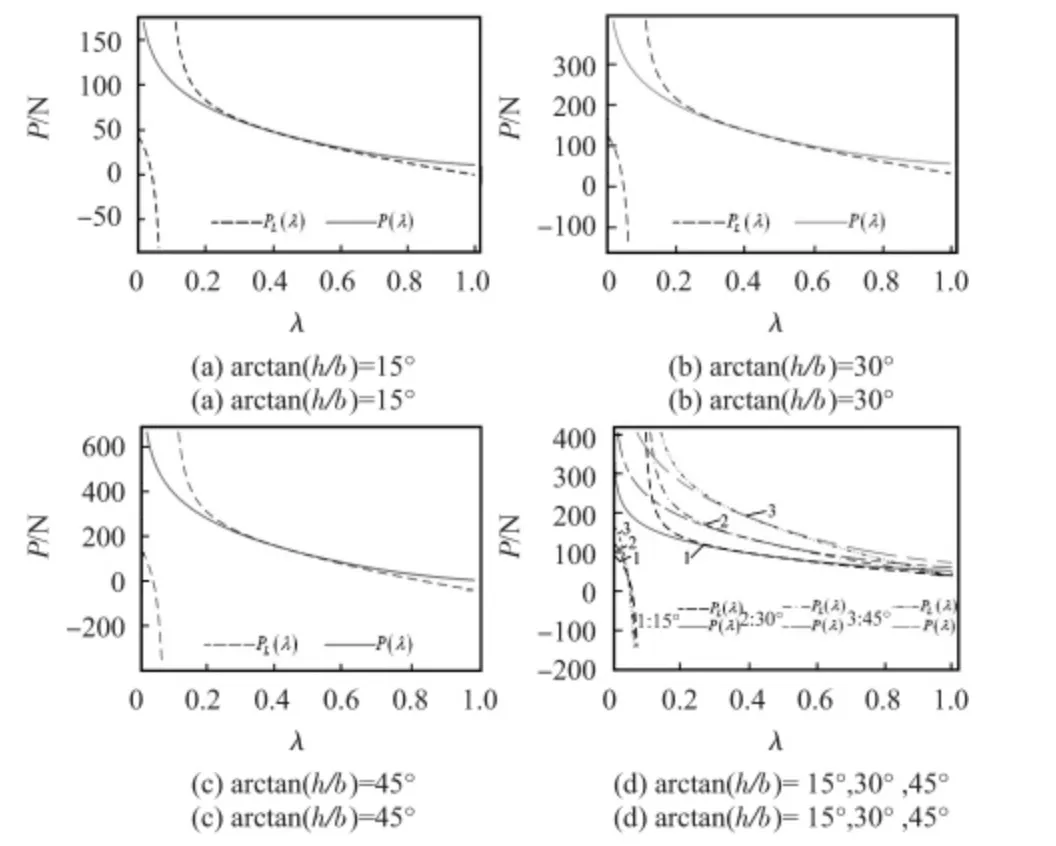
图4 不同结构尺寸对应P-λ 曲线图Fig 4 P-λ curves with different sizes of structure

图5 广义Kelvin 模型示意图Fig 5 Diagram of generalized Kelvin model

根据生物力学的基本知识，可以用以下数学形式对图5所示的模型进行描述

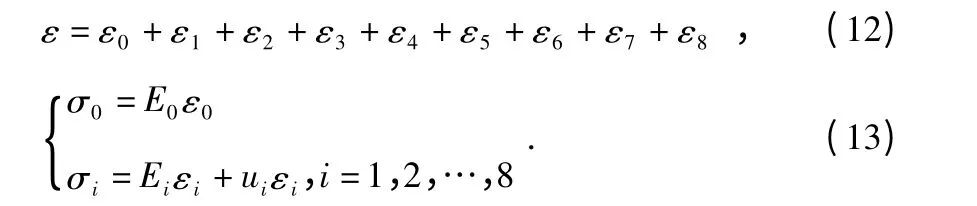
将式(13)代入到式(12)当中，并做相应的拉普拉斯变换，得到线粘弹性软组织材料的表达式

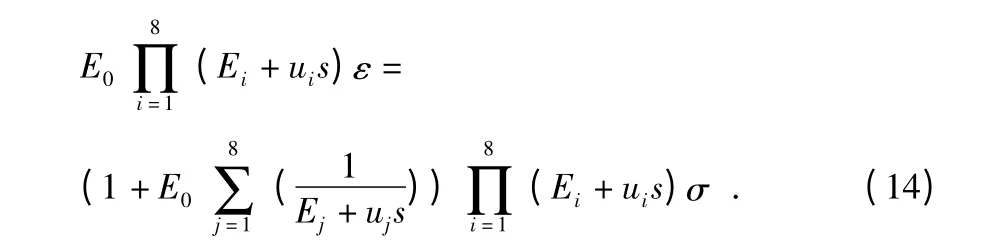
2.3 粘弹性体接触模型

用遗传算法得到猪的左心房肌肉组织广义Kelvin 模型的本构参数［9］，可以简化式(14)，具体数值如表1 所示。

根据式(14)和表1，可以求得猪心脏软组织剪切模量Gs

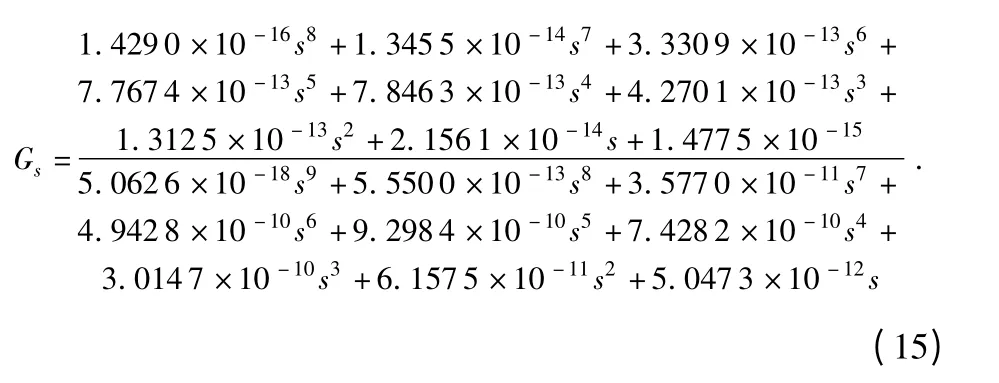
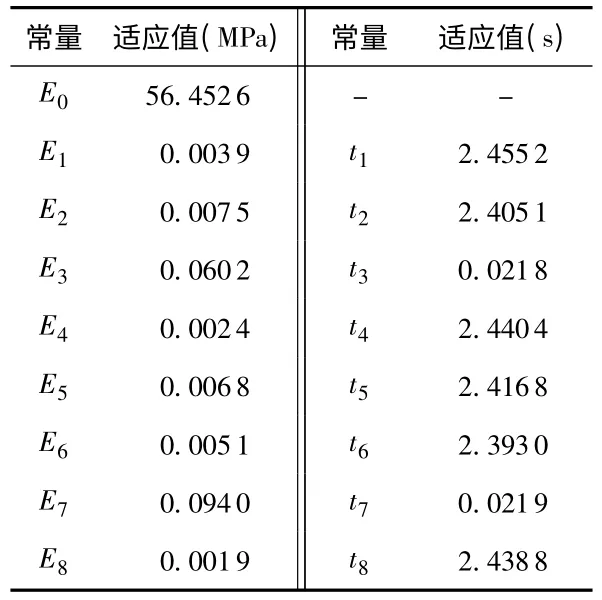
表1 广义Kelvin 模型的本构参数Tab 1 Constitutive parameters of generalized Kelvin model

取泊松比ν 为0.5，软组织的剪切模量如式(15)已确定，式(8)和式(10)可分别转换成

式(16)、式(17)即为触觉传感器与猪心肌肉组织间的接触模型。可见，载荷P 决定于参数h，d，λ 和Gs。利用拉普拉斯逆变换将式(16)和式(17)从频域函数变换成时域函数。在进行逆变换之前，先确定一些常数项:b=2.5 mm，arctan(h/b)=15°，ν=0.5。假定一系列λ 值(即软组织变形程度)，并根据分界点，将其代入到式(16)和式(17)所对应的时域函数中，得到不同λ 值所对应的不同P-T 曲线，如图6 所示。

图6 可见，载荷P 随着时间变化总是从一个较大的值迅速减小再趋于稳定。这正是粘弹性材料性质。此外，图6也证实，当λ 越小时，在稳定时所需要的力就越大。稳定时，所需要的力都远小于3.5 N，这避免了器械对健康的软组织会造成不必要的伤害［10］。

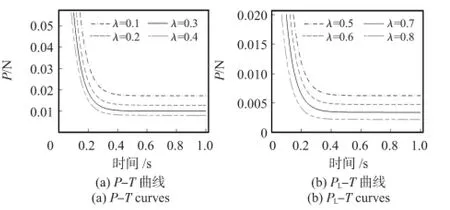
图6 不同λ 值对应P-T 曲线图Fig 6 P-T curves with different values of λ

3 实 验

本次实验被测对象为五种不同硬度的材料，编号分别为A，B，C，D，E。其中，A 为PDMS187，B 为704 硅橡胶，C，D，E 是类似橡胶的材料。用邵氏硬度计测得其硬度如表2所示。

表2 材料硬度测量值Tab 2 Measured values of hardness of materials

为了验证原理，简化实验，实验中传感器仅贴入三处压阻材料，各处位置对应的λ 值分别为0.8，0.5，0.2，如图7所示。

图7 压阻材料粘贴位置示意图Fig 7 Diagram of position of piezoresistance materials

实验方案:将三种压阻材料分别接入到三个电桥电路当中，作为电路中的可变电阻器，供电电压为10 V。传感器与软组织位置关系如图8。用已标定的钢片在传感器顶端施加压力后，根据电压的变化来判别压阻材料是否受到变形软组织的挤压，从而判断软组织变形程度，确定接触半径ai。实验采用USB4716 数据采集卡对电桥电路输出电压进行采集，并用LabVIEW 编程，对数据进行了分析处理。

传感器实物如图8 所示，为了简化实验难度，适当地扩大了实验样机模型，同时仅在凹面内贴入了三处压阻材料。

图8 传感器实物图Fig 8 The figures of experiment sensor

首先进行了固定载荷加载试验，加载力分别为1，2，3N，通过比较相同的载荷所产生的变形程度来区别材料软硬度。检测结果表明:五种材料的硬度关系为:A ＞B ＞C ＞D ＞E。这与硬度计检测的结果相符。

根据接触模型，对五种材料的剪切模量进行求解。判断出要达到指定的变形量所需要的力，将相应的λ 值和对应的力的值代入到式(8)或式(10)中，即求得对应的剪切模量。表4 给出了要使材料变形部分刚碰到相应位置所需要的载荷大小。将其代入到接触模型中，可以求得各材料的剪切模量分别为GA=0.019 2 MPa，GB=0.012 3 MPa，GC=0.001 6 MPa，GD=0.000 9 MPa，GE=0.000 3 MPa。从各剪切模量也能判断其硬度之间的关系。参考相关文献可知，这些计算值在材料相关参数范围之内［11］。因此，可以证实该传感器是可行并且有效的。

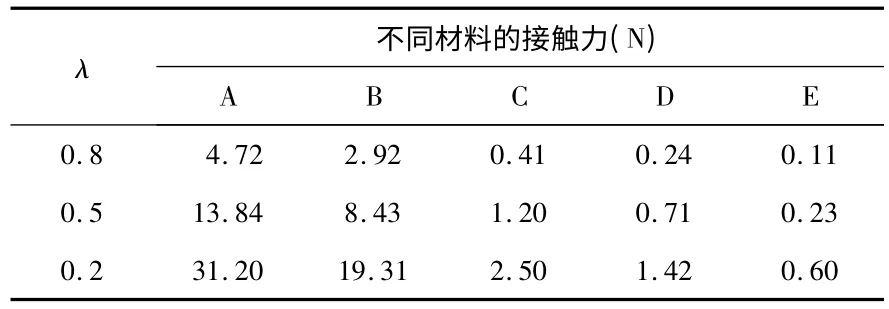
表4 接触力判断Tab 4 Judgement of contact force

4 结束语

实验证明:该传感器能有效地辨别材料相对硬度，最主要是能计算出软组织的剪切模量，并且结果处在常规材料参数范围内，具体精度有待进一步考证。目前，凸面体或平面体与软组织间接触模型研究较多，但凹面体与软组织间接触问题分析甚少。该接触模型解法同样适用于其他内凹面物体与软组织之间的接触问题。

［1］ Wisitsoraat A，Patthanasetakul V，Lomas T，et al.Low cost thin film based piezoresistive MEMS tactile sensor［J］.Sensors and Actuators A:Physical，2007，139(1):17－22.

［2］ Yip M C，Yuen S G，Howe R D.A robust uniaxial force sensor for minimally invasive surgery［J］.IEEE Transactions on Biomedical Engineering，2010，57(5):1008－1011.

［3］ Tanimoto M，Arai F，Fukuda T，et al.Micro force sensor for intravascular neurosurgery and in－vivo experiment［C］∥Proceedings of The Eleventh Annual International Workshop on Micro－Electro－Mechanical Systems，MEMS’98，IEEE，1998:504－509.

［4］ Kalantari M，Ramezanifard M，Ahmadi R，et al.A piezoresistive tactile sensor for tissue characterization during catheter－based cardiac surgery［J］.The International Journal of Medical Robotics and Computer Assisted Surgery，2011，7(4):431－440.

［5］ Ahmadi R，Dargahi J，Packirisamy M，et al.A new hybrid catheter－tip tactile sensor with relative hardness measuring capability for use in catheter－based heart surgery［C］∥2010 Conf on IEEE Sensors，IEEE，2010:1592－1595.

［6］ Collins W D.On the solution of some axisymmetric boundary value problems by means of integral equations，Potential problems for a circular annulus［C］∥Proc of Edinburgh Math Soc，1963:235－246.

［7］ Barber J R.Indentation of the semi－infinite elastic solid by a concave rigid punch［J］.Journal of Elasticity，1976，6(2):149－159.

［8］ Grinberg G A，Kuritsyn V N.Diffraction of a plane electromagnetic wave on an ideally conducting flat ring and the electrostatic problem for such a ring［J］.Zhur.Tekh.Fiz.1961，31(1):743－749.

［9］ Shen J J，Kalantari M，Kovecses J，et al.Viscoelastic modeling of the contact interaction between a tactile sensor and an atrial tissue［J］.IEEE Transactions on Biomedical Engineering，2012，59(6):1727－1738.

［10］Wagner C R，Howe R D，Stylopoulos N.The role of force feedback in surgery:Analysis of blunt dissection［C］∥International Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems，IEEE Computer Society，2002:73－73.

［11］Nunes L C S.Shear modulus estimation of the polymer polydimethylsiloxane(PDMS)using digital image correlation［J］.Materials and Design，2010，31(1):583－588.