UTM投影坐标系下厂站工程控制测量

高春林，朱照荣

(1．国核电力规划设计研究院，北京100095;2．北京市测绘设计研究院，北京100038)

一、引 言

随着中国“走出去”战略及国际化进程的深入，大批中国企业走出国门到海外承包工程，尤其是在一些非洲国家，非洲国家坐标系统大都采用6°带UTM投影，很多工程由于UTM投影长度变形相对较大(不足1/10 000)，满足不了工程测量规范“测区内投影长度变形不大于2．5 cm/km”的要求。很多中国企业在解决工程UTM投影长度变形问题时，采用国内惯用的解决高斯投影变形的处理方法，即通过抵偿高程面或采用任意带方法，有的则直接采用高斯投影坐标，业主要求UTM坐标成果时，再通过坐标变换成UTM投影坐标系。这些方法都或多或少地存在一些不足，采用抵偿高程面的方法解决不了参考椭球面投影变形与UTM投影面变形“同号”的情况。任意带的方法使得测量与当地国家统一坐标不一致，不便于内外之间的联系，直接采用高斯投影，与业主要求的UTM投影坐标间存在一个比例系数，工程设计及施工放样需要缩放比例，比较麻烦。本文通过对UTM投影变形特点的分析，对比高斯投影坐标系下长度变形，以及对工程控制网的理解，提出了国外UTM投影坐标系下的电厂及变电站工程控制测量方法。

二、UTM投影坐标系下的长度变形分析

UTM投影(universal transverse mercator)全称为“通用横轴墨卡托投影”，是一种等角横轴割圆柱投影，圆柱割地球于南纬80°、北纬84°两条等高圈，投影后两条相割的经线上没有变形，而中央经线上长度比0．999 6。UTM投影是为了全球战争需要创建的，美国于1948年完成这种通用投影系统的计算。这种投影的长度变形限制在1/1000之内。这样既保持了正形投影的性质又改善了变形分布，因而被世界上许多国家所采用(如图1所示)。

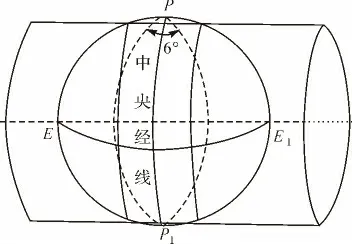
图1 UTM投影示意图

UTM投影变形包括两项，地面水平距离投影到参考椭球面的长度变形和参考椭球面上的边长投影到UTM投影面的长度变形。其中1 km地面水平距离投影到参考椭球面的长度变形ΔS1约为

式中，Hm为测距边高出参考椭球面的平均高程;R为测距边所在法截线的曲率半径。

参考椭球面上1 km边长投影到UTM投影面的长度变形ΔS2为

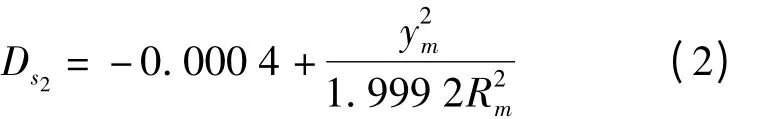
式中，ym为归算边两端点横坐标平均值;Rm为参考椭球面平均曲率半径。

由式(1)和式(2)实测1 km水平距离归算到UTM投影面的长度总变形ΔS为

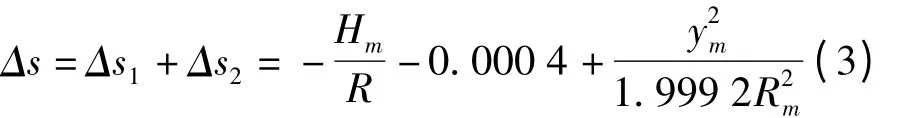
在不考虑参考椭球面长度变形的情况下，由式(2)可知，在南纬15°附近，UTM投影和高斯投影(GAUSS)变形量与横坐标Y对应关系如图2所示，从图2可以看出，UTM投影与高斯投影变形的特点。

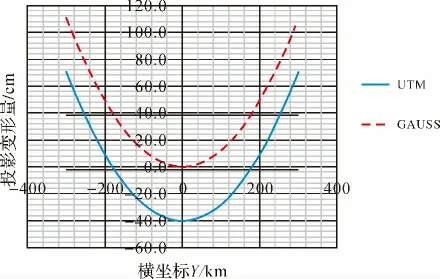
图2 UTM与GAUSS投影变形图

1)UTM投影和高斯投影的变形值均呈对称型，但高斯投影变形均为正值，且离中央子午线越远变形越大，而UTM投影在中央子午线处负变形值最大，离中央子午线越远负变形越小，直到东西各约180．3 km(约1°45')的两条割线上，投影变形值为0，离开这两条割线越远则正变形值越大。

2)UTM投影中央子午线上变形值最大约－40 cm/km，在［－180．3 km，180．3 km］区域UTM投影变形值与参考椭球面变形“同号”，不能通过改变高程投影面来抵偿，而高斯投影所有区域的变形与参考椭球面变形“反号”，任何区域可通过改变高程投影面来抵偿。

3)UTM投影在［174．7 km，185．9 km］，［－185．9 km，－174．7 km］区域变形量不超过2．5 cm/km，即经差［1°42'，1°49'］，［－1°49'，－1°42'］两区域带宽之和总共不超过22．4 km，而高斯投影变形量不超过2．5 cm/km的带宽约为90 km。

在工程初设及施工图阶段，为了降低投影变形，在我国地形图按要求一般采用高斯投影3°分带，而在国外，UTM投影一般都是按6°分带。

如果考虑参考椭球面长度变形情况，由于参考椭球面的长度变形为负值，而且UTM投影中央子午线东西各约180 km范围内，UTM投影变形值为负，两者叠加，变形值为负的范围会更大。因此，国外UTM投影坐标系下的工程测量，大范围区域内采用抵偿高程面方法，并不可行。

三、对工程控制网的理解

(1)工程控制网与国家大地网有所区别。工程控制网主要用于工程设计阶段大比例尺地形图测量以及工程建造阶段工程施工放样，直接为工程设计及施工服务，而非服务于国家基本比例尺地形图测量。而国家大地控制网主要是为国家经济建设提供统一的参考框架，为测量国家基本比例尺地形图服务;工程控制网一般来说控制范围有限，而国家网控制整个国家，因此国家网要采用一定的投影方式，并把成果归算到一定的椭球面上。

(2)因为工程是建立在地表面上的，不是建造在椭球面上，工程网本质上应在地表面上，准确地说在测区平均高程面上讨论问题，而不应该到椭球面上讨论问题。事实上，很多工程椭球面与地表面高程差距很大。

(3)工程控制网应首先满足工程设计及施工的本质安全需要，其次才考虑别的要求。工程设计要求由工程地形图上量取的距离直接为实地施测的距离，工程施工放样要求由坐标反算的距离与地面测量的距离相等。

(4)工程控制网内符合精度是第一位的，其次要保证一定的外符合精度，外符合用于本工程定位以及测区内外、测区与当地其他规划之间的联系;而工程本身的设计及施工建造要求测量控制网具有较高的内符合精度。

(5)工程控制网可以不按照国家网的基准原则和要求执行。工程测量规范规定:测区投影变形在满足2．5 cm/km的前提下，工程控制网可以采用国家统一坐标、抵偿高程面、任意带等处理方法，言下之意是测区投影变形大于2．5 cm/km的情况下，工程控制网可以不采用国家统一坐标系，而采用其他的坐标系统，所采用的坐标系统只要长度变形满足2．5 cm/km精度要求，就能保证工程设计及施工建造的本质安全。

基于对工程控制网的以上几方面，笔者认为工程控制网应在测区平均高程面或施工高程面上考虑问题。无须到椭球面、投影面上去考虑问题，对于小范围测区(小于10 km×10 km)无须进行投影计算，直接假定平均高程面是一个平面，在此平面上进行几何平差计算。

四、UTM投影变形超限处理方法

基于以上UTM投影变形特点及对工程控制网的理解，如果将测区内部控制网(控制整个测区的)建立在测区平均高程面或施工高程面上，则可以消除参考椭球面的投影长度变形。如果假定测区平均高程面是一个平面，那么就无须在测区平均高程面上进行UTM投影面归化计算，直接基于测量观测数据进行平面几何平差计算即可(严格讲观测边长应进行平均高程面归化计算)。这样，投影面变形可以被消除。由于厂站工程面积相对较小，尤其是变电站，小于10 km×10 km，直接把局部地球表面平均高程面假定为一个平面是可行的。由此，若满足以上两个假设，则两项UTM投影长度变形可全被消除。如果工程控制网的坐标联测(联测国家已知点)完全按照国家大地网的UTM投影方法及平差原则进行，则与已知点联测的测区控制点与已知的国家控制点性质一样，具有一定的外符合精度。

这种UTM投影长度变形超限的处理方法需要做的工作是:联测点的平差要在国家网原则下进行，内部网平差时，需选择一个与已知国家点联测的点作为投影中心，将该点坐标投影到测区平均高程面上，并将该点作为起算点，在测区选择该点到另一个联测点的方位角作为起算数据，该方位角可通过两个联测点的国家坐标系坐标反算得到。平差元素为地面观测值归算到测区平均高程面上的值。这种解决UTM投影变形超限的方法弥补了通过抵偿高程面以及采用任意带方法解决投影变形方法的不足，既解决了参考椭球面与UTM投影面变形“同号”的情况，又实现了工程内外之间的联系，而且，提供的坐标成果又是业主要求的UTM投影坐标。

五、工程实例

赞比亚330 kV输变电工程位于赞比亚北方省内，线路全长约387 km，共设计Pensulo、Mpika、Kasama 3个330 kV变电站。Pensulo变电站位于东经30°26'，南纬13°02'左右，测区平均海拔1560 m;Mpika变电站位于东经31°24'，南纬11°52'左右，测区平均海拔1375 m;Kasama变电站位于东经31°9'，南纬10°14'左右，测区平均海拔1325 m。赞比亚位于东非，其国家地图投影采用6°分带UTM投影，国家坐标系统采用ARC 1950，椭球为Clark 1880 modified ellipsoid。由式(3)可得，Pensulo变电站总的变形约为30．5 cm/km，Mpika变电站总的变形约为－24．6 cm/km，Kasama站址总的变形约为－10．6 cm/km，3站址的UTM投影变形均超过2．5 cm/km的工程测量规范要求。

本工程3个变电站采用上述方法解决UTM投影长度变形超限问题。坐标联测利用收集到的国家控制点使用Trimble GPS按静态测量方式进行，每个站布设6个控制点，Pensulo变电站采用已知点ZP114，联测两个未知点PS1、PS6，Mpika变电站利用已知点TS471，联测未知点MP1、MP6，Kasama站址利用已知点ZP112，联测未知点KS1、KS6，坐标转换采用三参数转换(赞比亚全国统一采用)，得到各个变电站联测点的赞比亚UTM国家统一坐标。各个站内控制网采用GPS静态测量模式，起算点采用一个联测点坐标，一个由两个联测点反算的方位角。GPS基线结算得到的基线向量不进行高程面及投影面归化计算，只将其归算到各个变电站的平均高程面上，利用控制网平均高程面上的边长进行常规的平面几何平差。该方法平差出的控制点坐标与赞比亚UTM国家坐标近似，坐标最大相差25 cm。

六、结束语

国外工程测量与国内工程测量主要的区别是国家坐标系统采用的投影方式可能不同，国外大多采用6°带UTM投影，而我国采用3°带高斯投影。本文通过对UTM投影长度变形的分析以及对工程控制网的理解，提出了一种解决国外UTM投影变形超限的方法，并将其应用到赞比亚330 kV输变电工程测量实践中。这种方法较适用于电厂、变电站等范围相对较小(10 km×10 km)的中小型工程，也适用于采用高斯投影的国内工程，对于覆盖面较大的大型工程，可适当考虑分区假定平面的方法，或采用任意带UTM投影方式。

［1］ 张凤举，张华海．控制测量学［M］．北京:煤炭工业出版社，1999．

［2］ 孔祥元，梅是义．控制测量学(下册)［M］．武汉大学出版社，2002．

［3］ 刘明波，雷建朝．UTM投影及投影变形处理［J］．西北水电，2010(6):21-25．

［4］ 叶达忠，谢家业．国际工程测量的UTM投影变形及抵偿分析［J］．广西师范学院学报:自然科学版，2009，26(1):34-39．

［5］ 袁小勇，陈功．国际工程中UTM投影变形的应对策略——以苏丹某电厂为例［J］．工程勘察，2010(5):15-21．

［6］ 王俊，王夺．毛里塔尼亚努瓦克肖特新国际机场控制测量［J］．勘察科学技术，2008(3):19-24．