基于弹性力学思想的河流等高线冲突自动处理方法

2015-03-29王光霞贾奋励

测绘工程 2015年12期

刘芳，王光霞，侯璇，贾奋励

（1．61175部队，江苏南京210049；2．信息工程大学地理空间信息学院，河南郑州450052；3．南京市栖霞区体育局，江苏南京210046）

河流等高线冲突是数字地图中常见的错误之一。在数字制图中，地图综合的位移操作是解决河流等高线冲突的有效方法。位移是在许可的范围内最大限度地保持目标的定位精度，并在尽量保持目标整体特征、相互关系以及排列特征的情况下，移开有冲突的目标［1］。河流等高线冲突属于目标间冲突，只需要对目标的局部范围进行调整即可解决，不需要对目标整体位移，即牺牲目标的部分形状特征换取目标大部分区域位置精度的方法。

线目标位移的算法很多，大致可分为机械式算法和优化算法。这两种算法都能解决一定的位移问题，但是机械式算法的收敛性不好，不能控制位移的传播，会产生新的冲突；优化算法效率较低，且不能保证解决所有的原始冲突。

弹性力学是固体力学的一个分支，主要研究弹性体受到外力作用或温度改变等原因而发生的应力、形变和位移［2］。弹性体变形的基本特征是保持目标空间关系的大体不变性，符合制图综合中位移的效果，特别是其中的杆件受力变形与位移有许多共同之处，因此可以用于解决河流等高线的冲突问题。由于平面杆件弹性体的受力变形模型十分复杂而导致无法利用传统的解析方法求解。因此本文采用数值计算中的有限元法解决此问题。

1 弹性力学原理与有限元方法

弹性力学的基本思想是当物体受到一定外力作用时产生形变，当外力撤消时又恢复原形；如果仅仅是物体的部分受力，则在变形时物体的总体形状基本保持不变，只是局部变形［3］。该特点符合数字制图中处理河流等高线冲突的基本原则，因此采用这一思想对河流等高线冲突进行检测和纠正。作为弹性目标结构，等高线受到来自于河流的引力作用而发生形状改变。

有限元方法是一种数值计算方法，它主要用于求解复杂结构或非线性方程组。其基本思想是将连续的求解区域离散为一组有限的、且按一定方式相互连接在一起的单元组合。然后利用每个单元内假设的近似函数来分片地表示整个求解区域上待求的未知场函数。单元内的近似函数通常由未知函数及其导数在单元的各个结点的数值和其插值函数来表达。因此，未知场函数及其导数在各个结点上的数值就成为新的未知量（即自由度），从而使一个连续的无限自由度的问题变成离散的有限自由度的问题。如果单元是满足收敛要求的，近似解最后将收敛于精确解［3］。其基本步骤有5个：物体的离散化、挑选形函数或插值函数、确定单元的性质、组成物体的总性质方程组、解方程组［4］。

在本文研究的问题中，河流、等高线作为地理相关目标，具有一定的形态结构特征，即河流总是流经谷底。因此河流与等高线的交点必然是谷底点，若河流与等高线的交点与谷底点不重合，则需要将等高线上的交点移动到谷底点位置。从弹性力学角度讲，可把等高线视为一个弹性体，一个点的受力变化必然会引发相邻点的受力改变，因而其位置也相对移动，且这种改变会逐渐减小并消失，这就保证了目标的相对空间关系不会发生较大改变，达到期望效果。

2 河流等高线冲突探测

冲突探测是算法中的重要问题。本文将入库数据中河流等高线的冲突归纳为两种情况。第1种是河流与等高线的交点不在谷底点上，如图1中数字1标识的位置，这种情况可以通过对等高线进行局部变形来解决。第2种情况是一条河流与同一条等高线有多个交点，如图1中数字2标识的位置，这种冲突情况处理较为复杂，需要人工干预。第1种情况可以通过本文算法进行自动纠正；第2种情况较为复杂，必须通过人工纠正。

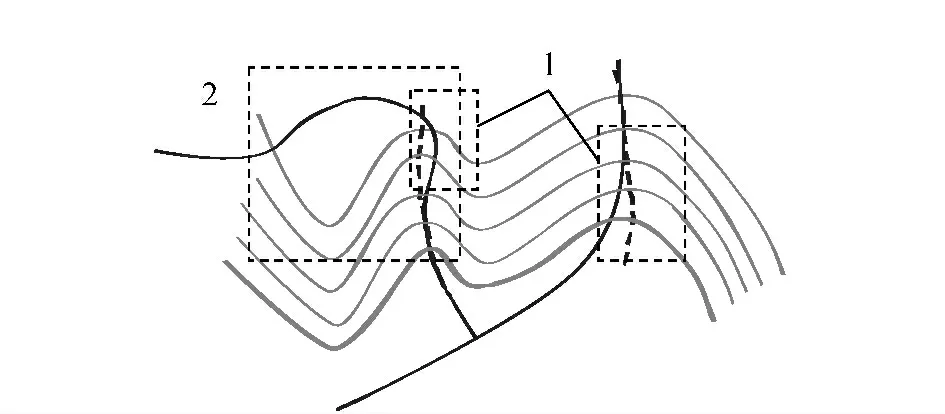
图1 河流等高线冲突情况

2．1 河流等高线求交点

经分析可知，河流等高线发生冲突的位置在二者的交点附近，因此冲突探测的第一步就是求交计算。本文采用向量跨立求交算法。所谓跨立是指某条线段的两个端点是否与另一线段所在的直线相交，采用叉积方法来确定。其设计思想：首先从点条的辅叉P1助积与出线，以发段及向P另1P的一3方线和向与段P。1的 P若两4，两个然的个端后叉叉点计积积P算，的3从和正而P负判4相与断引反向出，两量则P3P4跨立P1P2所在的直线，如图2（a）所示；若两个叉积的正负号相同，则P3P4不能跨立P1P2所在的直线，如图2（b）所示；若任何一个叉积为0，则P3和P4两点中必有一点处于线段P1P2所在的直线上，如图2（c）所示。

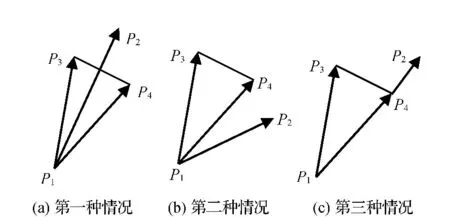
图2 向量跨立求交算法

只有两线段的叉积正负相反时，才对河流和等高线进行求交计算，同时记录交点所处河流的点位、等高线点位及该段河流的坐标。去除伪交点和重复交点，并将交点按照河流的ID号排序。伪交点包括以下2种情况：交点位于线段的两个端点；求交线段中的某条位于另一条线段的同一侧。

2．2 求谷底点

定义1 假设河流等高线交点附近的一段等高线上的n个点｛P0，P1，P2，…，Pn｝为待定谷底点集合。

定义2 交点处的河流向量为River Vector，交点为Intersection Pt。

定义3 假设河流等高线交点位于P1和P2之间，则等高线向量。

由谷底点的几何性质可知［5－6］，谷底点为等高线上的局部曲率最大点；河流向量River Vector总是位于等高线向量Contour Vector的顺时针方向。根据以上两点性质可以确定谷底点。河流向量与等高线向量的关系归纳见图3。图3（a）和图3（c）中河流向量在等高线向量的逆时针方向，这时首先需要将待定谷底点集合｛P0，P1，P2，…，P5｝逆序排列，然后计算最大曲率点即谷底点；图3（b）和图3（d）中河流向量在等高线向量的顺时针方向，此时直接计算所有待定谷底点的曲率值，最大曲率点即为谷底点。具体步骤如下所述。

图3 谷底点与河流向量到等高线向量方向的关系图

1）计算向量River Vector到向量Contour Vector的方向，采用二者的叉积判断，如果为叉积小于0，则为逆时针方向，需要将待定谷底点集合逆序排列。

2）对处理后的待定谷底点集合求曲率，除首、末点P1，Pn外任意点Pi的曲率Curi可以根据式（2）求得

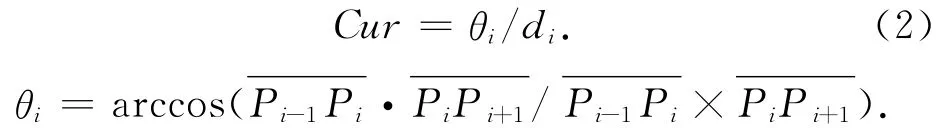
其中，θi为向量Pi－1Pi和PiPi＋1的夹角；di为弧段Pi－1PiPi＋1的长度。当θ一定时，其对应的弧长d越小则曲率越大，由此可以计算出弧段内的最大曲率点，即谷底点。

3 强制位移量的确定

得到谷底点和冲突点信息后，下一步需要确定消除冲突部分所需的最小位移量，即冲突部分完全移动到冲突线的另一侧时所有可能位移方向中距离最小的一个向量［7］。具体可以分为如图4所示的3种情况，其中Pb为谷底点，Pc为冲突点。

1）当冲突点位于河流线段的中间，强制位移量为谷底点到最近的河流线段的最小距离，方向垂直于河流线段，如图4（a）所示。

2）当冲突点位于河流线段的始端点，强制位移量为谷底点到该点的最小距离，方向为谷底点与该点的连线，如图4（b）所示。

3）当冲突点位于河流线段的末端点，强制位移量为谷底点到该点的最小距离，方向为谷底点与该点的连线，如图4（c）所示。

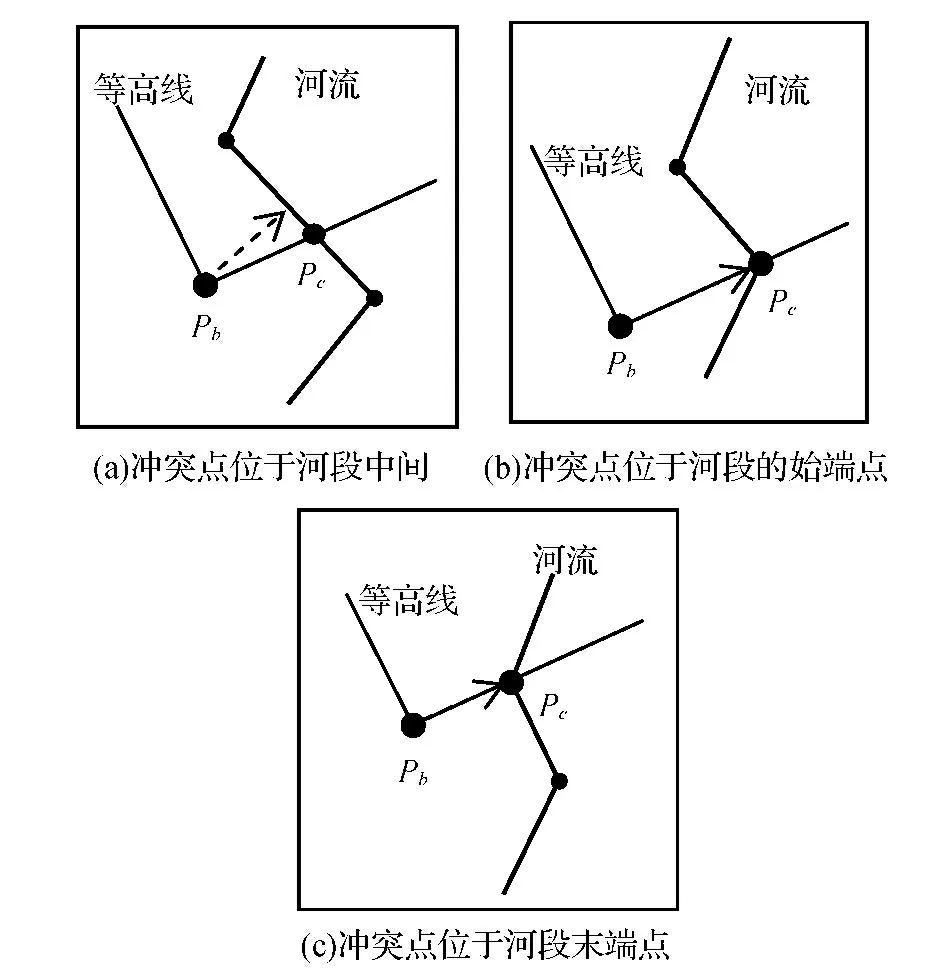
图4 计算强制位移量示意图

当强制位移量过大时，如果强行移动会破坏整个弹性体的弹性，从而导致位移结果变形。因此对于超过阈值范围的冲突点，不能用这种方法自动纠正，需要记录其坐标，方便人工处理。

4 目标的变形方法

4．1 建立单元刚度矩阵

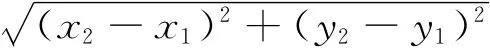
其中，KG为考虑横剪力的杆全局坐标刚度单元，E为弹性系数，s＝sinα，c＝cosα。

4．2 确定并集合相关的变形目标

在制图综合中，河流等级和精度高于等高线，因此在二者冲突时，应当改变等高线的形状。等高线构成了空间杆件结构，改变一个顶点往往会引发其他相关顶点的相应变动，所以在操作过程中要对所有需要变形的地点进行适当处理，使相关顶点形成一个整体，然后对这个整体进行变形操作，只有这样才不会破坏原目标的整体结构。文中的相关顶点个数是个经验值（20），与等高线采集的密度及其地貌特征相关。这些顶点属于不同的单元，并且在总刚度矩阵中的位置相同。多个目标公用一个结点，通过这个公用的结点，不同目标的刚度矩阵集合到一起。把每一个有强制位移量的顶点看作一个平面杆状目标，这样带有强制位移量的顶点集合就构成了所有变形目标的集合。

4．3 求解方程

仔细观察式（3），可以看出它是一个奇异矩阵，只有引入足够的约束条件消除其奇异性，才能得到唯一解。在这里约束条件就是前文计算的强制位移量，它是通过冲突探测和制图约束条件分析得到的。引入约束条件的方法有多种，在程序计算中可以采用能求得精确解的置1赋0法。

将方程中给定位移σ的行和列的主元改为1，其余全部置0，并将原来矩阵的第i行除对角线元素外乘以给定位移σ后移到等式另一端，对应的第i行的右端项Fi改为σ，修改后方程变为

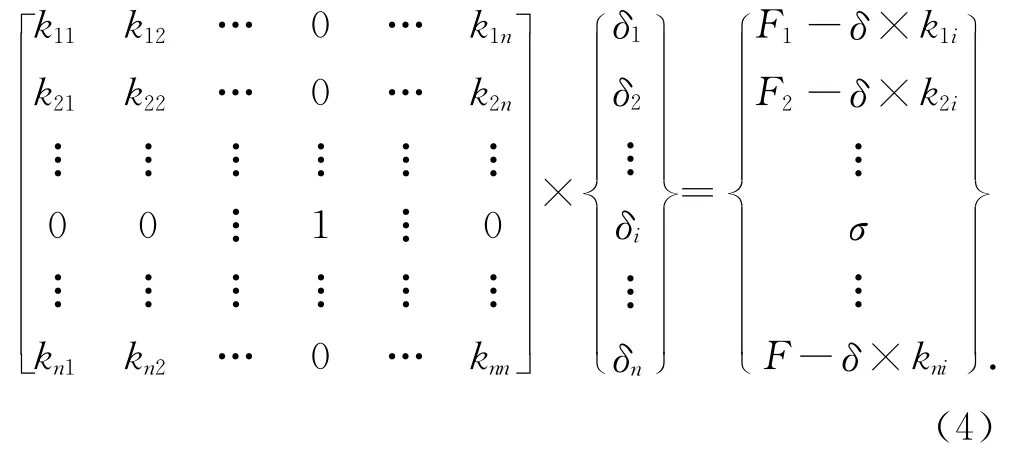
显然方程第i行等价于σi＝σ。

由式3可知，对位移有影响的参数有弹性系数E、弯曲惯性矩I、横截面A。不同参数配置得到不同的位移变形结果。E越大杆件越不易变形；A越大杆件的伸缩性就越好；I越大杆件就更易于弯曲。根据制图综合规则和等高线变形等级，本文实验中给它们赋值如下：E＝5，I＝2，A＝0．851。

5 实验与分析

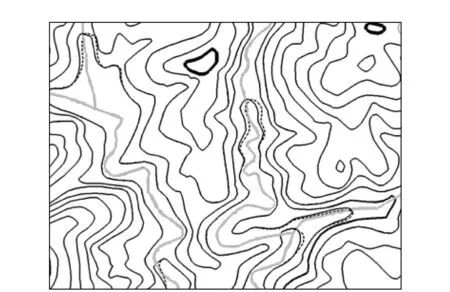
图5 试验效果

采用1∶5万数字地形图作为试验用图，结果如图5所示。其中灰色线为河流，黑色实线为位移后的等高线黑色虚线为位移前等高线从图5中可以看出，只有产生了冲突的地方得到了修正，等高线形态保持较好，并且等高线与水系的关系保持较好，处理结果基本满足制图综合约束条件的要求。

表1列出了实验使用的3幅1∶5万地形图中河流等高线冲突的检测点数以及进行位移操作的各项参数。其中位移点数表示有冲突的点数，最大角度变形指所有相邻线段的夹角的最大变化值。从表1中可以看出对冲突点的修正率达到80%以上。在检测出来的待位移点中，有一部分冲突是河流爬坡，还有一些是超过最大位移量的冲突点，这类冲突需要人工解决。经过该算法纠正的冲突点，无论x轴方向还是y轴方向，位移量都未超过1 mm；且最大角度变形和位移传播范围都能满足制图综合的要求。位移后的等高线也能够保持基本形态。

表1 1∶5万地形图中河流等高线冲突检测及纠正结果表

6 结束语

本文提出的基于弹性力学思想的河流等高线冲突处理方法具有几何不变性、差异性和使用方便的特点，综合后等高线和河流的形态及相互关系保持较好，应用方便。实验证明该方法处理后的结果能够达到生产精度要求，可以推广使用。该算法的缺点是计算较为复杂，时间耗费较长。本文研究仅适用于单线河与等高线发生冲突的情况，对于河流穿同根等高线、河流爬坡等冲突的自动检测与修正问题，需进一步研究。

［1］武芳，侯璇，钱海忠，等．自动制图综合中的线目标位移模型［J］．测绘学报，2005，35（3）：269－276．

［2］徐芝纶．弹性力学［M］．北京：高等教育出版社，1990：210－254．

［3］李人宪．有限元算法基础［M］．北京：国防工业出版社，2002：1－4；188－190．

［4］侯璇．基于弹性力学原理的自动综合位移模型［D］．郑州：信息工程大学，2004：5－34．

［5］王强，曹辉．数字地形图中河流线与谷底线空间冲突自动检测及纠正［J］．测绘通报，2010（12）：58－61．

［6］ GALANDA M．Automated Polygon Generalization in a Multi Agent System［D］．Zurich：Depart ment of Geography，University of Zurich．2003：13－18．

［7］刘芳，钱海忠，侯璇．基于弹性力学思想的GIS多源数据误差纠正方法［J］．测绘工程，2009，16（1）：1－5．

［8］楚彬，范东明．改进的多元线性回归模型及其应用［J］．测绘工程，2014，23（6）：63－66．

［9］蒙印，艾廷华，杨井源．1∶250 000水系要素综合缩编技术方法［J］．测绘与空间地理信息，2014，37（3）：201－203．

［10］夏永亮．基于复杂网络理论的城市道路网络自动综合方法［J］．测绘与空间地理信息，2014，37（8）：155－156．

［11］宋少辉，魏东岚，王雪．基于Map Basic的等高线赋值设计与实现［J］．测绘与空间地理信息，2014，37（11）：121－123．

［12］郭薇，郭菁，胡志勇．空间数据库索引技术［M］．上海：交通大学出版社，2006：4－43．