基于载波相位差分的北斗／GPS双模定位系统研究

马文忠，李林欢，江丽丽

（中国石油大学（华东）信息与控制工程学院，山东 青岛266580）

目前，多模卫星定位导航技术相关研究引起了广泛关注，利用北斗与GPS系统之间的互操作性和兼容性，可以减小定位误差，保证导航系统的高质量。在现有的设备条件下，卫星接收机的测量精度不变，如果能利用好数据处理方法，比如用相对定位取代单点定位，可以把定位精度提高一到二个数量级［1－2］。载波相位差分定位技术作为相对定位中的一种方式，采用载波相位观测量来实时确定用户的具体位置，通过测站间作差及卫星间作差，消除卫星钟差和接收机钟差，减小设备误差、电离层延迟和对流层延迟、轨道误差等对定位结果的影响，可以提高定位精度至厘米级［1－4］。北斗／GPS双模导航系统克服了单GPS系统有较强的依赖性和潜在危险性等缺点［3－4］，将北斗、GPS观测数据进行格式、时间、坐标转换和伪距组合等一系列的数据融合，统一求解，实现连续实时、自动化且精确地监测用户位置情况，载波相位静态差分定位算法，在数据处理时，既能保证定位监测的精度，又满足快速性的要求。

1 基于信息融合技术的北斗／GPS双模导航系统

开发兼容GNSS（Gl obal Navigation Satellite System导航系统的多模 低能耗和高灵敏度卫星信号接收机是一个重要研究方向。为实现北斗／GPS信号的融合，设计中频北斗／GPS双模单射频通道接收机，包括天线单元、射频开关、射频通道单元、数字基带处理单元、信息处理单元，还包括一个频率合成单元及控制单元。控制单元控制高频射频开关使通道切换，控制频率合成单元产生本振信号的频率，控制模数转换器选择相应模式。实现了既能单接收北斗卫星播发的B1频点信号，产生10．23 MHz≤f1≤13．299 MHz的北斗中频信号，也可单接收GPS卫星播发的L1频点导航信号，得到9．207 MHz≤f2≤12．276 MHz的GPS卫星中频信号，还可同时接收北斗、GPS卫星信号，而后经过基带的调制、解扩等处理，得到译码后的码状态和载波相位等数据观测量。用户通过微处理器、存储器及一些配套的输入输出设备，计算连续获取所需的完好性信息［9－12］。

系统运行如图1所示，在监测位置设置一台北斗／GPS双模接收机作为监测点，在地质条件良好的地方另设一台接收机作为基准点，两者组成一条基线。对静态相对定位来说，监测点的位置坐标突出了“相对”性，最终的结果为监测点与基准点之差（Δx，Δy，Δz），称其为基线向量。让两接收机在同一时间段内同步接收双模观测信号，利用观测数据融合解算基线向量。

图1 北斗／GPS双模导航定位监测系统

双模接收机能接收L1，L2频段的GPS信号和B1，B2频段的北斗信号。载波相位观测值可用式（1）和式（2）表述，G代表GPS卫星，C代表北斗卫星。

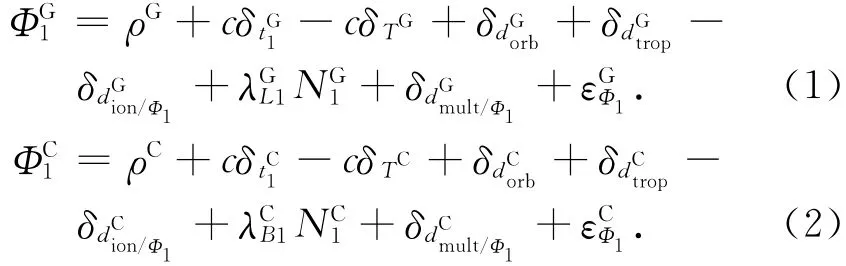
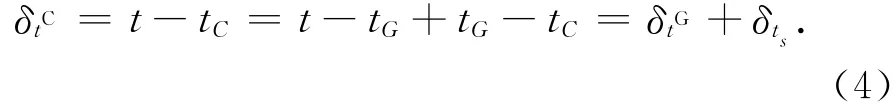
代入式（2）

将上式线性化处理，

其中，

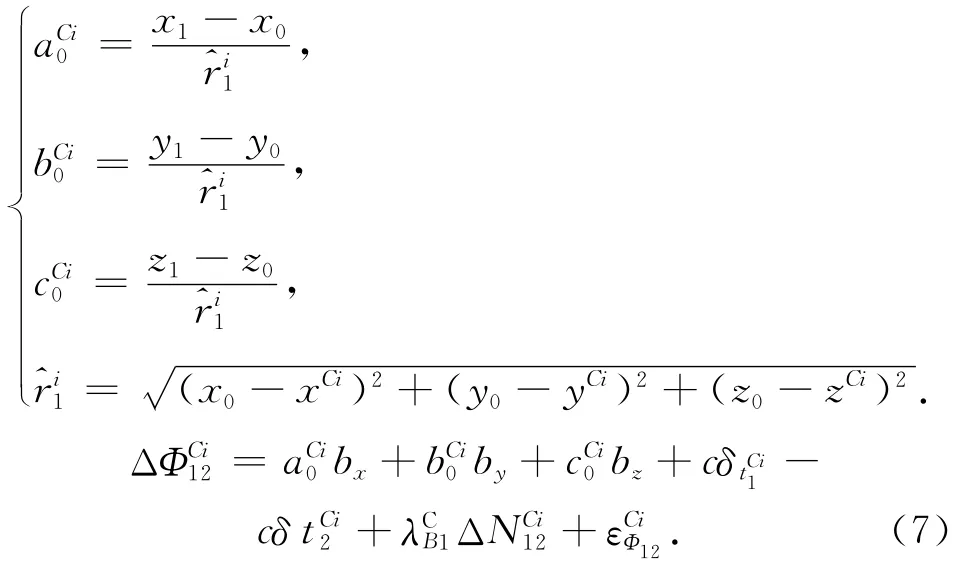
求双差观测方程，

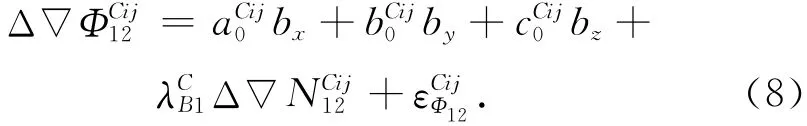
在某一历元接收到M颗GPS、N颗北斗卫星信号时，得出M＋N－2维双模定位模型，

在以后的历元中，如果基准站和监测站能够一直保持对这M＋N颗卫星的同步观测，那么当方程个数大于或等于未知数个数时，就能够求解监测站三维坐标的偏差d x，d y，d z和整周模糊度

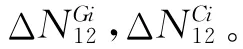
2 北斗／GPS载波相位差分定位实现方法

北斗与GPS的系统组成、定位原理和编码方式等相同，从信息融合的角度来看二者是可以兼容的。对于联立得到的北斗／GPS双模载波相位双差监测系统，其数据处理过程跟GPS相似［13－15］。

2．1 观测数据和星历数据的读取

在分析静态相对定位用在北斗／GPS双模定位导航系统中的可行性基础上，首先对原始数据进行处理 所使用数据为RINEX格式的观测数据和导航电文［5］具体程序流程见图2。NAVfile为单颗卫星在导航电文中的所有数据，包括卫星的PRN号、星历参考时间、星钟参考时间及改正数、开普勒轨道参数。

图2 读取导航电文的流程图

2．2 卫星位置的计算

卫星的钟差及位置可以使用精密星历来计算，精密星历可以到IGS站点下载，向后时延从实时到11天不等。SP3格式给出的是间隔15 min离散的位置和钟差，因此需要使用拉格朗日多项式插值法来获得高精度的卫星钟差及位置。用迭代的思想来求解信号发射时刻的GPS系统时。利用式t＝ts－f（t），其中f（t）为拉格朗日插值公式，各节点的值为观测记录的GPS周内秒计数，各节点对应的函数值为卫星钟差。表1是2012－01－01的精密星历部分卫星钟差内容。

表1 部分卫星精密星历钟差 us

利用拉格朗日插值法求ts＝10 800时刻的卫星钟差，结果如表2所示。计数结果表明，以信号发射时刻的卫星钟时间t作为迭代初值，一次迭代和二次迭代之间的差值已经非常小，因此在实际应用中 只迭代一次即可得到满足精度要求的结果 求出信号发射时刻的GPS系统时后，就可以用它来求卫星的三维坐标。

表2 精密星历卫星钟差计算结果 us

2．3 双差观测方程组的形成及求解

双差观测方程的形成是非常重要的部分，用最小二乘法求解观测方程组［8］。程序主要结构如图3所示。对于方程组中的矩阵，使用稀疏矩阵来存储和计算，可以减少程序内存的消耗并提供程序的执行效率。用3个行向量来记录一个稀疏的矩阵A，它们分别是V，J和I。V中的元素为稀疏矩阵中所有非零元素的合集，J中的元素为V中元素在A中的列标，I中的元素为A中每行第一个非零元素在V中出现的位置的下标。

图3 程序整体框图

稀疏矩阵

则有V＝［3 1 6 1 4 2］，J＝［2 4 1 1 3 2］，A＝［1 3 4 6］。这种表示方式为按行存储，当然也可以按列来存储。其优点在于只存储了非零元素及所在位置 运算的时候也只有非零元素参与运算。

3 北斗／GPS双模导航定位中的难点

使用静态相对定位方法对用户的位移进行监测，双差观测方程彻底消除了卫星钟差和接收机钟差影响，设计选星算法，并解决方程中的周跳探测、整周模糊度未知数计算问题，可以运用基准站和监测站的同步观测数据求解观测站的坐标。

3．1 卫星定位中的几何分布精度因子研究

通过对用户位置的求解，得到了在线性化点用户位置Δx与伪距偏差ΔL之间的关系，如果不考虑观测误差的影响，上述问题可简单地转化为最小二乘问题。

由协方差阵式（11）和式（12）知，GDOP大小与定位误差成正比，GDOP值越小，伪距观测值的方差σ0越小，定位精度就越高。

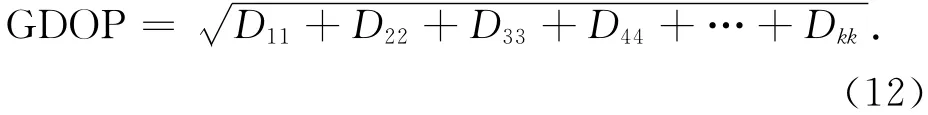
由图4和图5中可看出，GPS单系统时，GDOP值曲线不太连贯，其平均值在2．5左右，而双模系统的GDOP值曲线是连续平滑的，其平均值稳定在2左右。在卫星截止角设置相同的情况下，GPS单系统构成的星座几何分布特性比北斗／GPS双模系统差很多，北斗卫星系统的加入提高了观测条件困难时导航定位的精度。在研究GDOP值与定位精度之间关系的基础上，以此为标准设计选星算法，选择几何分布最佳的卫星星座组合，提高接收机处理速度，节省硬件成本。

如图6所示，分析上海司南接收机北斗／GPS静态相对定位实验得到的数据，图中横轴表示观测历元，纵轴表示当前历元可见卫星数。

选取其中近12 000个历元，GPS单系统定位时，全时段有78．39%的路段可见卫星数大于10颗，北斗单系统全时段有11．45%的可见卫星数大于10颗。北斗／GPS双模系统在有北斗作为第二系统辅助增强后，在观测全时段中可见卫星数在15～20颗之间，定位能力提高至98．97%。北斗／GPS双模系统的应用，实现了导航监测网厘米级的精确定位。

图4 单GPS系统GDOP值变化

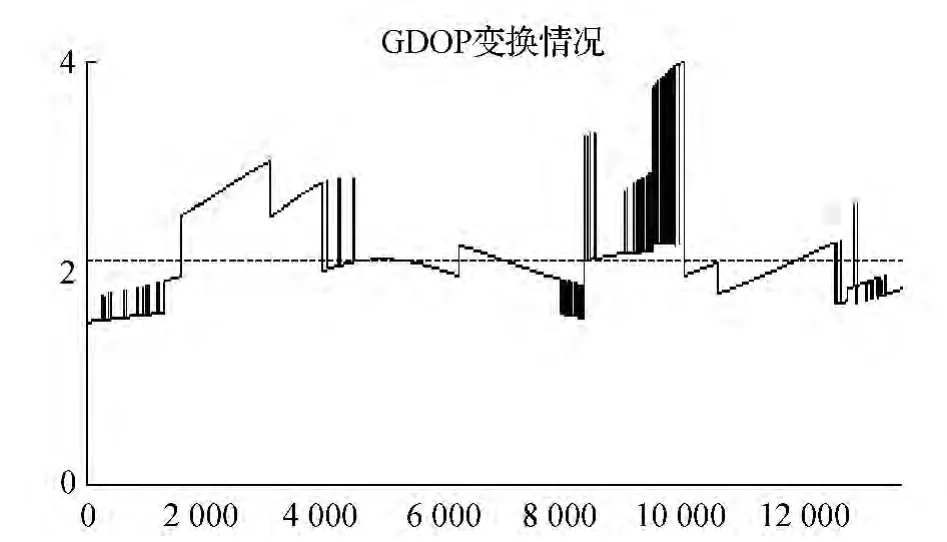
图5 北斗／GPS双模系统GDOP值变化

图6 相对定位卫星可见性分析

3．2 周跳探测及处理

如果接收机载波相位观测值φ发生周跳而没有检测出来，会将误差引入双差观测方程组，使定位结果产生很大误差［6］。通过对周跳问题的研究和对不同类型周跳数据处理后，本文总结出一套能够有效探测周跳的方法，如图7所示。

如图8和图9所示，接收机对PRN号为2的卫星观测一天得到的数据，历元间隔为30 s，共2 880个历元。图8中高上去的部分表示观测到了卫星，低下去的部分表示没有观测到卫星。图9为各个历元的宽巷模糊度。

图7 周跳探测的过程

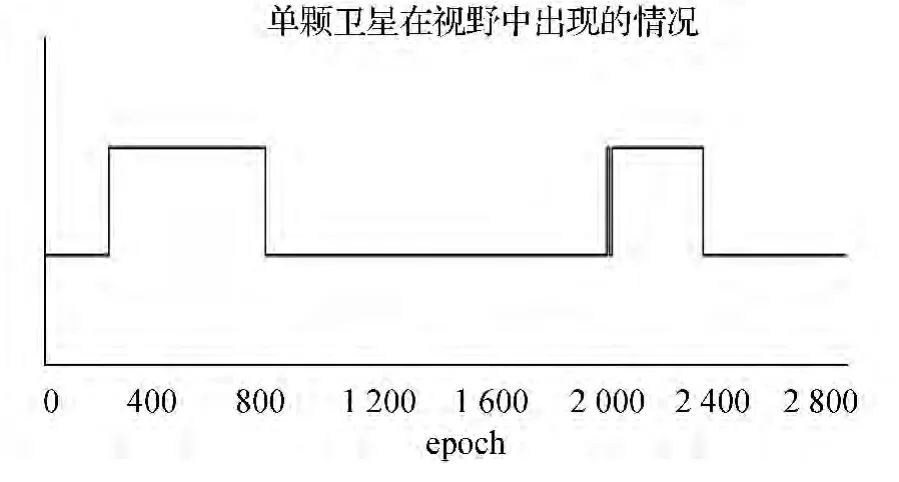
图8 2号卫星一天内在视野中出现的情况

图9 2号卫星一天内卫星宽巷模糊度曲线

图10 为图9中从第2 000到第2 380历元的宽巷模糊度的变化情况，可以看到在第2 293历元的宽巷观测值明显偏离了平均值，但下一历元的宽巷模糊度值又回到了平均值附近，所以该历元为粗差，不是周跳。而在第2 359历元及以后历元，宽巷值都高于了平均值，判断为周跳。

3．3 整周模糊度的确定

使用LA MBDA搜索算法可以搜索最佳的模糊度向量［7］。采用mobn和mobk两个站点在2012－01－01的同步观测数据作为相对定位的计算数据。选取mobk为基准点，mobn为监测点。同步观测数据的时间间隔为30 s，一天内共2 880个历元。取前400个历元的观测数据经过周跳和粗差剔除后，组成双差观测方程组。解法方程得到基线的初始解，共产生了17个实数模糊度。然后用LA MBDA方法将模糊度固定为整数。表3给出了双差观测方程组中模糊度的实数解和整数解。

图10 2号卫星详细的宽巷观测值的变化情况

表3 整周模糊度的确定

按照上面的观测资料运算结果的观测值单位权均方差为σ0＝5．6 mm，X坐标的精度为σX＝0．3 mm，Y坐标的精度为σY＝0．2 mm，Z坐标的精度为σZ＝0．8 mm。由此可见，随着基线长度的增加，静态相对定位的精度也随之降低。为了便于比较，用监测站坐标代替基线向量。由表4可见，模糊度的确定对基线向量的固定解是非常重要的。

表4 确定整周模糊度前后基线向量的变化

本文采用了SOPAC Scripps Or bit and Per manent Array Center）提供的IGS站的精确坐标作为参考，对中石油管线上mobk和mobn两个站点进行了基线向量解算（mobk为基准站，mobn为监测站），基线向量的定位结果如表5和表6所示。表5为北斗／GPS双模系统定位结果，表6为GPS单系统定位结果，分析两表数据，使用北斗／GPS双模系统能够进一步改善定位精度。

表5 北斗／GPS双模系统mobn定位结果和参考值对比

表6 GPS单系统mobn定位结果和参考值对比

4 结 论

通过深入研究北斗／GPS双模系统的载波相位差分定位技术，提出能够比较精确定位用户三维位置的完整算法。选取几何分布较优的卫星组合参与定位，利用最小化GDOP提高定位精度。将历元间载波观测值与星站距离作双差法与MW和GF组合法相联合，并对卫星在短时内反复出现和消失的情况进行滤波，剔除卫星仰角较小时的观测值，以此解决了整周跳变问题。研究整周模糊度确定的问题，利用等权模型进行平差运算，给出观测值权阵的推导，用LA MBDA方法确定模糊度后回代求固定解，得到位置解算误差较小的定位结果。分析中石油公司输油管线上实验数据，得出北斗／GPS双模载波相位静态差分定位技术处理流程及解算算法具有安全有效性，比单一系统在观测条件较差、截止高度角较大时，对系统的定位性能有明显改善，提高定位系统的准确性和安全性。同时，得出1 k m以内的基线，精度能够达到1 c m左右，但随着基线长度的增加，定位精度就将有所下降。通过研究码相位观测量与载波相位观测量多历元实时联合建模算法、卡尔曼滤波算法来消除测量误差，进而提高定位精度，改善定位性能。

［1］ 李征航，黄劲松．GPS测量与数据处理［M］．武昌：武汉大学出版社，2005：41．

［2］ 中国人民解放军总装备部军事训练教材编辑工作委员会．GPS技术与应用［M］．北京：国防工业出版社，2004：6－12．

［3］ 李征航，张小红．卫星导航定位新技术及高精度数据处理方法［M］．武昌：武汉大学出版社，2009：28－29．

［4］ 孙洪瑞，沈云中，周泽波．GPS／GLONASS组合点定位模型及其精度分析［J］．测绘工程，2009，18（1）：8－10．

［5］ 国家测绘局．GB／T 18314－2009全球定位系统（GPS）测量规范［S］．北京：中国标准出版社，2009：2－6．

［6］ 孔巧丽等．星载GPS相位非差观测粗差和周跳的探测与修复［J］．大地测量与地球动力学，2005，25（4）：105－109．

［7］ 李一鹤，沈云中，李博峰．基于LA MBDA方法的GPS动态相对定位［J］．测绘工程，2011，20（1）：6－10．

［8］ 楚彬，范东明．基于比例整体最小二乘的GPS高程拟合［J］．测绘工程，2014，23（4）：37－39．

［9］ GURTNER W．Astrono mical Institute University of Bern．The Receiver Independent Exchange For mat Version 2．0［Z］．2009－6－22．

［10］马瑞峰．基于北斗导航定位系统的伪卫星技术研究［D］．西安：西北工业大学，2005．

［11］GLEASON S，GEBRE－EGZIABHER D．GNSS应用与方法［M］．杨东凯，译．北京：电子工业出版社，2006：112－176．

［12］GURTER W．Astr ono mical Instit ute University of Ber n．The Receiver Independent Exchange For mat Version 2．0［Z］．2009－6－22．

［13］RA MAKRISNAN S，GAO D X，LORENZO D D．Design and Analysis of Reconfigurable Embedded GNSS Receivers Using Model－Based Design Tools［C］．ION GNSS 21st International Technical Meeting of the Satellite Division，2008：2293－2303．

［14］韩波．北斗卫星导航定位系统［J］．中国计量，2004（3）：22－23．

［15］CHEN X，KANG R．Searching algorith m with granularity changing and the GNSS integer ambiguity estimation［C］／／Co mputer and Inf or mation Science，2009．ICIS 2009．Eighth IEEE／ACIS International Conference on．IEEE，2009：44－47．