时间序列协整关系及其在变形分析中的应用研究

张 拯，张献州

（西南交通大学 地球科学与环境工程学院，四川 成都610031）

随着变形监测领域软、硬件的不断革新，变形监测所获得的数据正向着海量化、多种类、多维数的方向发展，如何从这些纷繁复杂的监测数据中提取出可用于变形分析、预测的有效信息问题亟待解决。目前，用于变形监测数据处理分析的方法有很多，相应的分析预测手段也各有其优点［1］。时间序列分析是一种处理随时间变化而又相互关联的动态变形分析方法［2］，它从统计自相关的角度出发，研究随机动态数据序列的规律。由于实际观测条件的复杂性，单个测点的观测时间序列往往不具有平稳性，建立在平稳数据变量的基础上的经典时间序列分析模型，处理非平稳变量会出现失真、虚假结果。目前，对于非平稳监测数据序列常规做法是对单个非平稳时间序列采用差分方法消除序列中含有的非平稳因子，使得序列平稳化后再利用时间序列分析建立模型，但变换后的序列由于不具有变形监测的直接意义，使得基于变换后的序列所建立的时间序列模型不便于变形解释分析。1987年Engle和Granger提出的协整理论及其方法，为非平稳序列的建模提供了另一种途径，可用于提取非平稳监测数据序列中的变形信息。时间序列协整关系是对非平稳变量长期均衡关系所进行的统计描述［3－4］。通过对非平稳序列进行某种线性组合（协整向量）使得组合后时间序列的单整阶数降低，以减小时序分析的复杂程度，并得出其中的线性均衡关系，以建立序列的结构模型，从而可以进行预测分析。变形监测数据可看作是随时间变化的动态序列，通过一定的线性组合方式构建两个或多个时间序列数据之间的协整关系，可实现组合序列的平稳性，表现为线性组合序列的矩，如均值、方差或协方差等随时间平稳变化，基于这种有规律的变化可实现变形监测的分析预测。本文采用时间序列分析及其协整关系对同一变形体的不同监测点的变形趋势进行分析，从非平稳监测序列中发掘出有效的变形信息

1 时间序列协整关系

若所考虑的时间序列具有相同的单整阶数，且存在某种线性组合（协整向量）使得组合时间序列的单整阶数降低，则称这些时间序列之间存在显著的协整关系［5－6］。假定k维向量Yt＝（y1t，y2t，…，ykt）′的分量间存在协整关系，且Yt被称为（d，b）阶协整，记为Yt～CI（d，b），如果满足：

（1）y1t，y2t，…，ykt都 是d阶 单 整 的，即Yt～I（d），要求Yt的每个分量yit～I（d）；

（2）存在非零向量β＝（β1，β2，…，βk），使得β‘Yt～I（d－b），0＜b≤d，则称Yt是协整的，向量β又称为协整向量。

协整关系存在的条件是：只有当两个变量的时间序列｛x｝和｛y｝是同阶单整序列时，才可能存在协整关系［5］。注意到，同一监测对象的各变形监测点的位移时间序列都是同阶单整序列，因此可利用时间序列协整方法对其进行处理，以获得有效、显著的变形信息。

2 ARI MAX模型

2．1 ARI MAX模型说明

ARI MAX模型是指带回归项的ARMA模型，回归项的引入大大提高了模型的预测效果，ARIMAX模型中所引入的回归项一般与变形预测分析的研究对象（被解释变量）紧密相关。以往利用ARI MAX模型描述研究对象变形规律时，只是构建了含有一个输入序列的ARI MAX模型，实际情况是：影响时间序列的因素除其自身变化规律外，往往还和其他多个时间序列的变化有关。由于模型的先天性缺陷，利用单一时间序列的ARI MAX模型（或ARMA模型）均无法恰当地描述变形分析中多元时间序列的变化规律，因此，本文研究建立含有多个时间序列的ARI MAX模型，并将其运用于变形分析之中。

2．2 ARI MAX的构造思想

假定因变量序列（响应序列）｛yt｝和自变量序列（输入序列）｛x1t｝，｛x2t｝，…，｛xkt｝都是平稳序列，首先建立两者的回归模型：

式中：Φi（B）为第i个输入变量的自回归系数多项式，Θi（B）为第i个输入变量的移动平均系数多项式，li为第i个输入变量的延迟阶数，｛εt｝为回归残差序列。

（1）式移项得残差序列｛εt｝的表达式：

由于｛yt｝和｛x1t｝，｛x2t｝，…，｛xkt｝都是平稳的，所以（2）式中所示残差序列也是平稳的。使用ARMA模型提取残差序列｛εt｝中的相关信息，最终得到动态回归模型，简称ARI MAX：

式中，Φ（B）为残差序列自回归系数多项式；Θ（B）为残差序列移动平均系数多项式，at为零均值白噪声序列。

2．3 ARI MAX模型建立步骤

1）平稳性检验。首先对因变量序列｛yt｝和各自变量序列｛xit｝做平稳性检验。序列具有平稳性是时序建模的重要前提［3］。平稳序列可极大地减少随机变量的个数，简化时序分析的难度，同时也提高了特征统计量估计精度。平稳序列具有两个重要的统计性质：

a）常数均值：EXt＝μ；

b）自协方差函数和自相关函数仅与时间间隔有关：γ（t，s）＝γ（k，k＋s－t）。

序列平稳性检验方法有两种，一种是图示法，即根据时序图和自相关图显示的特征判断序列的平稳性，另一种是构造检验统计量的假设检验法（常用单位根检验）。

2）生成自变量序列的白噪声序列。对2．2中经适当差分后平稳的自变量序列｛xit｝建立ARI MAX模型，以产生白噪声序列｛εxit｝：

3）生成因变量序列的白噪声序列。对经过差分后平稳的因变量序列｛yt｝也实施（4）中同样的变换：

4）确定ARI MAX模型结构。考察所生成的两个白噪声序列｛εxit｝和｛εyit｝的互相关系数以确定动态回归模型结构：

5）考察残差序列｛εt｝，并对其拟合模型：

3 运用ARI MAX建立时间序列模型

运用ARI MAX模型进行时间序列建模的核心思想就是通过构建相应的ARI MAX模型 对平稳序列（原序列及其变换序列或残差序列）中自相关信息进行提取，实现对观测序列的拟合。数据列之间具有自相关性是建立时间序列模型的基础［3］。假定某个观测值序列已经进行了预处理，如果序列非平稳并进行平稳化，并判定处理后序列为平稳非白噪声序列，我们就可以利用ARI MAX模型对该序列建模。其建模步骤如图1所示。

图1 平稳序列建模步骤

3．1 模型识别

模型辨识是根据样本观测值xt（1≤t≤n），计算其自相关系数｛，0＜k＜n｝和偏相关函数｛，0＜k＜n｝值并由＾φkk和＾ρk是否截尾判定模型是AR（p）还是MA（q）。

自相关系数＾ρk和偏自相关函数＾φkk为随机变量，当样本容量n→∞时，有～N（0，），～N（0，）。它们不可能具有严格截尾性（绕0做小值振荡），需要借助数理统计方法来判断它们的截尾性：

3．2 模型参数估计

模型参数估计，是在模型结构及阶次已确定条件下，对模型参数φj（1≤j≤p），θj（1≤j≤q）与σ2ε进行估计。常用条件最小二乘（OLS）估计法：假定xt＝0，t≥0，亦即认为ε1＝ε2＝…＝εp＝0；当p≪n时，可以忽略前p个εt对Q（~β）的影响。如果已知n－p个观测值，ARMA（p，q）模型（混合模型）所包含方程的向量形式为：

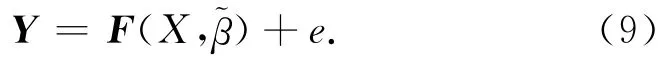
式中，Y＝（xp＋1，xp＋2，…，xn）T，F＝（fp＋1，fp＋2，…，fn）T，e＝（εp＋1，εp＋2，…，εn）T，X为观测值向量（x1，x2，…，xn）。于是，残差平方和为：

由于Q（~β）不是~β显性函数（F（X，~β）为非线性），未知参数最小二乘估值可用迭代法求出或取定初值β0 可取矩估计值 进行展开或按非线性解法进行。最小二乘估计充分利用了序列观测值的信息，其估计精度很高。

3．3 模型的适用性检验

通常对残差的平方和进行F检验做出参数的选择和定阶，首先对观测数据用ARMA（p，q）模型进行过拟合，再假定φp，θq高阶系数中某些取值为零，用模型残差平方和来衡量低阶模型与高阶模型之间的差异［6］。

假定原假设H0：φp＝0，θq＝0，记Q0为ARMA（p，q）模型的残差平方和，Q1为ARMA（p－1，q－1）模型的残差平方和，则构造F统计量

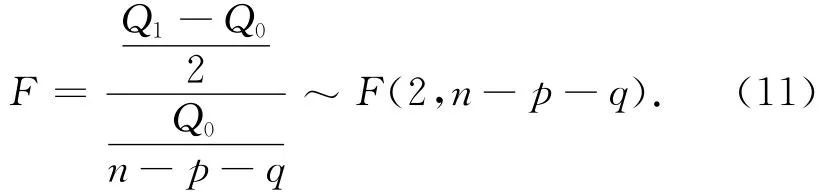
若F＞Fα，则拒绝原假设H0，模型阶数仍有上升的可能；否则原假设H0成立，即选择ARMA（p－1，q－1）模型。

3．4 模型优化

对一个实际问题可以建立多个有效模型（即有效模型不惟一），需要从中选择出相对最优的模型，即模型优化。通常采用AIC和SBC信息准则进行模型优化。

最小信息量AIC准则是从衡量拟合程度的似然函数值和模型中未知参数的个数两方面（加权函数）考察一个拟合模型的好坏。通常似然函数值越大模型拟合效果越好，同时未知参数的个数越少越好。所以一个好的拟合模型应该是一个拟合精度和未知参数个数的综合最优配置。

对于ARMA（p，q）模型其对数似然函数为

AIC准则参数个数权重始终为2，在n→∞时，它通常比真实模型所含的未知参数个数要多。因此，定义SBC准则为

对于ARMA（p，q）模型

3．5 模型预测

所谓预测就是利用已观测序列值的拟合模型对随机序列未来发展进行估计。常用的预测方法是线性最小方差预测。对于MA（q）序列，其ARIMAX模型为

MA（q）序列理论上只能预测q步之内的序列走势，超过q不预报值恒等于序列均值。这是由MA q序列自相关q步截尾的性质决定的

4 实例分析

4．1 工程概况

某地下隧道长度82．318 m，隧道埋深7～7．8 m，穿越花岗岩残积土层。地面上方横跨高速公路特大桥，地下水位较高，常水位在地面下1．5 m处。为了对大桥及路面进行有效的监测，首先在施工沉降影响范围以外埋设4个首级控制点G1、G2、G3、G4，之后在桥墩柱和重点路面埋设监测点。现选取其中几个典型监测点的42期监测成果用于动态建模分析，前面36期值参与建模，而最后6期数据用于对比分析。桥墩监测点Q21、Q5、Q6变形量表和时序图如表1和图2所示。

表1 桥墩监测点Q21、Q5、Q6变形量表 mm

图2 桥墩监测点Q21、Q5、Q6沉降时序图

由图2可以看出，桥墩监测点沉降时间序列均为不平稳时间序列，将它们进行1阶差分后即可变为平稳的非白噪声序列［6］。

4．2 基于时间序列协整关系模型预报

通过分析观测值序列，可以建立有效或相对最优时间序列模型，运用确定的模型就可以实现对序列未来的发展趋势作出预测 从而为变形体的安全分析提供依据，并对监测体的安全性提前预警，以便及时采取相应措施避免事故的发生。

利用单序列预测模型，对监测点Q21、Q5、Q6的沉降量进行预测 受篇幅限制 现取6期的模型预报值与实测值进行对比，如图3（a）、图3（b）、图3（c）所示。

图3 监测点预测值与实测值对比图

从图3可以看出，通过分析对监测点序列建立的时间序列模型，能够实现对监测点的未来可能发展趋势作出较为准确的预测。但随着预测步长的逐渐增加，预测精度变差，其拟合置信限曲线成喇叭状。

变形体的变形状态一般都用变形体上离散的特征点状态和位移量来描述［7］。由于各监测点会受到同一变形体整体效应的作用，离散监测点的变形趋势应趋于一致性。从图2可以看出它们之间具有基本相同的变化趋势。因此可以认为同一变形体上各点序列值之间存在着一种非常密切的长期均衡关系，具有内在的平稳同变性。根据时间序列之间的协整关系就可以研究各序列自身变化不平稳但其之间回归模型拟合后的残差序列平稳，从而建立ARI MAX动态模型。

假定Q6点监测数据为自变量（x），Q5监测数据作为响应序列（y），可构造回归模型

由于Q5、Q6间具有协整关系，利用条件最小二乘估计，可得到Q5的动态模型ARI MAX为

残差序列｛at｝为白噪声序列，模型拟合显著有效，并且参数显著非零。模型的信息量为AIC＝54．87，SBC＝59．62。显然，模型信息量更少，比单独Q5序列模型更优。此时模型的6期的预测值如表2所示。

通过对同一桥墩上多个监测点监测数据建立ARI MAX动态模型，对各点的沉降趋势进行预测，实现了同一变形体不同监测点之间的相互联系，为实现变形体的变形监测预报、安全评估提供了更为有益的思路。对比分析可知，ARI MAX动态模型相对于单序列预测更为优化，其预测结果更为可靠。

表2 点Q5时间序列模型6期预测值 mm

5 结 语

本文在研究时间序列特性的基础上，采用时间序列协整分析，从统计自相关的角度出发，研究非平稳随机动态变形监测数据序列的规律，从多测点变形监测数据中发掘出平稳的可用于变形预测的信息。理论分析和实践验证均表明：基于时间序列协整关系的ARI MAX动态预测模型可以有效提取出用于变形预测评估的有效信息，其预测结果是科学、准确的。时间序列协整关系为建立复杂变形体纷繁发杂的多测点海量变形监测数据综合监控模型提供了一种方法，进一步拓展了传统时间序列分析模型在现代变形监测数据处理分析中的应用

［1］ 黄贤源，隋立芬，范澎湃．几种最优滤波方法的分析和比较［J］．测绘工程，2007，16（3）：35－39．

［2］ 邱伟，黄腾，朱春宁．混合模型在沉降监测中的组合预测方法［J］．测绘工程，2014，23（4）：51－54．

［3］ 唐佑辉，黄腾，赵兵帅．GOM和时间序列组合模型在地表沉降预测中的应用［J］．测绘工程，2014，23（2）：70－72，80．

［4］ 臧妻斌，黄腾．时间序列分析在地铁变形监测中的应用［J］．测绘科学，2014，39（7）：155－157．

［5］ 曹广喜．向量分整时间序列的协整关系探讨［J］．河海大学学报：自然科学版，2006（4）：469－472．

［6］ 王燕．应用时间序列分析［M］．北京：中国人民大学出版社，2005．

［7］ 尚金光，张献州，官超伟．高速铁路沉降评估中工程沉降和区域沉降的可区分性研究［J］．测绘科学，2013，38（1）：84－86．