电网电压不平衡下串联型12脉波整流装置的频域谐波建模

王佳佳 周念成 王强钢 魏能峤

(输配电装备及系统安全与新技术国家重点实验室(重庆大学) 重庆 400044)



电网电压不平衡下串联型12脉波整流装置的频域谐波建模

王佳佳 周念成 王强钢 魏能峤

(输配电装备及系统安全与新技术国家重点实验室(重庆大学) 重庆 400044)

针对高压直流输电和大功率工业整流采用的串联型12脉波整流装置，在分析其整流等效电路工作原理的基础上，计及电压不平衡时相控整流电路的触发角偏移和换相重叠角，推导了正序和负序电压作用下12脉波整流的谐波耦合导纳矩阵，将两者整合建立电压不平衡下12脉波整流的频域谐波耦合导纳模型。该模型能解析计算整流装置产生的电流谐波，无需迭代。搭建整流装置实验测试平台，探讨12脉波整流的谐波耦合导纳矩阵元素分布特点，分析电压畸变率、不平衡度和触发角变化对模型准确度的影响，通过计算与实验对比，验证所提频域谐波模型的有效性。

12脉波整流 不平衡电压 谐波模型 换相重叠角 耦合导纳矩阵

0 引言

随着电力电子技术的发展，越来越多的大功率非线性整流设备接入电网，采用晶闸管的相控整流装置在电解、冶金和柔性输电等领域得到广泛应用[1-3]。大功率整流的电流和电压等级相对较高，对电网谐波危害也更严重，目前主要采用无源、有源滤波[4]或功率因数校正[5]以及多重化技术[1]等方法来降低注入电网的谐波。其中，12脉波相控整流因具有结构简单、可靠性高等优点被广泛应用[6-8]，特别在高压直流输电中最为常见。晶闸管整流的非线性以及电网不平衡电压作用，将导致整流装置交流电流出现显著的谐波畸变，给电网带来不可忽视的谐波污染。该谐波直接影响直流输电系统滤波器选型和参数设计，并会对其他电力设备造成不同程度的损害[9，10]。因此，需深入研究不平衡电压下12脉波整流的谐波特性，建立准确、实用的解析模型以计算其产生的电流谐波，为多脉波整流器设计、电网谐波潮流计算和谐波治理措施配置提供指导。

采用时域[11]和频域[12-14]方法均可对12脉波整流装置进行谐波建模分析，考虑到其谐波电压和电流存在时域非线性耦合，频域方法更能直观地表征出整流装置的谐波产生机理[15]。文献[8]利用调制函数推导三相相控整流的交流电流计算式；文献[13，14]利用频域分析法建立三相相控整流装置的谐波耦合导纳矩阵模型；文献[16]则利用谐波导纳矩阵提出无需迭代的谐波潮流算法。前述研究均认为电网为三相对称的理想情况，实际上由于负荷、线路参数不平衡以及电网不对称故障，均会使电网电压出现不平衡分量[15，17]，文献[17]针对不平衡电压下的三相相控整流电路，利用改进的开关函数对整流器谐波进行分析。但12脉波整流由移相变压器和两个三相整流桥构成，通过变压器产生两组存在30°相位差的三相电压[1，6-9]，使两组整流桥部分谐波可被相互抵消，在不平衡电压作用下的谐波特性与三相相控整流具有显著差异。12脉波整流的两个整流桥直流侧可串联，也可通过平衡电抗器并联，文献[18]推导输入电压不平衡时并联型12脉波整流器的交流电流计算式；而串联型12脉波整流主要应用于高压直流输电[9，11]，文献[19]针对不平衡电压改进串联型12脉波整流的开关函数，分析负序电压对直流电压谐波的影响。但均未给出12脉波整流的频域谐波耦合导纳模型，不能清晰确定非理想电网条件下整流器端电压与电流的关系。

本文分析了串联型12脉波相控整流电路的工作原理，探讨整流器端电压谐波与电流谐波的耦合关系，计及变压器漏感引起的换相重叠角以及电压不平衡时相控整流电路的触发角偏移，推导了正序和负序电压作用下12脉波整流的谐波耦合导纳矩阵，进而建立电压不平衡下串联型12脉波整流器的频域谐波解析模型。该模型将12脉波整流器表征为基于端电压基波、各次谐波分量的谐波电流源模型，通过导纳矩阵元素确定不同电压分量对各次谐波电流的贡献程度。

1 不平衡电压下串联型12脉波整流工作原理及交流侧电流推导

串联型12脉波相控整流装置结构[11，19]如图1所示，包括接线方式为Y0/Y0/Δ的三绕组变压器、2个结构和参数相同的三相相控整流桥(分别记为桥Ⅰ和桥Ⅱ)以及电阻R和电感L构成的直流负载，三相整流桥Ⅰ和Ⅱ直流侧串联连接。电网电压经二次绕组分别采用星形和三角形联结的变压器降压后，生成两组大小相等、相位相差30°的交流电压，再由整流桥Ⅰ和Ⅱ作用，在直流侧产生两组相位错开30°的直流电压u1dc、u2dc，叠加后使直流电压udc在每个周期内脉动12次。该直流电压作用于负载生成脉动的直流电流idc，再经整流桥与交流电网耦合，使12脉波整流器交流电流iabc发生谐波畸变。

图1 串联型12脉波整流电路Fig.1 Diagram of a series 12-pulse rectifier

正常运行时每个时刻12脉波整流电路有4个或5个晶闸管交替导通，图1中其交流电流iabc由桥Ⅰ和Ⅱ的交流电流i1abc、i2abc叠加而成。基于文献[14]的串联型12脉波整流装置谐波解析流程，如图2所示。根据三相相控整流桥Ⅰ和Ⅱ的交流电压，结合相应的电压开关函数，分别求得其直流电压u1dc和u2dc，相加得到12脉波整流装置的直流电压udc，该电压作用于负载生成直流电流idc，再由桥Ⅰ和Ⅱ电流开关函数调制，形成各自的交流电流i1abc、i2abc，叠加获得12脉波整流桥交流电流iabc，再利用该交流电流表达式推导12脉波整流装置频域谐波模型。

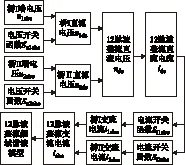
图2 串联型12脉波整流谐波解析流程Fig.2 Harmonic analysis process of series 12-pulse rectifier

由于电网不平衡电压的零序分量经开关函数调制后不会影响整流装置直流电压变化[19]，研究中仅考虑整流桥端电压的正序和负序分量。根据电压不平衡国标规定，整流装置端电压负序与正序分量之比，即三相电压不平衡度允许值为2%，短时不超过4%[20]。实际电网电压含若干奇次谐波分量，该电压经二次绕组星形联结、电压比为1∶kT的变压器降压后，生成三相相控整流桥Ⅰ端电压u1abc为

(1)

(2)

相控整流桥触发环节检测同步电压信号时，需滤除装置端电压的高频谐波和负序分量，将使其开关函数的触发角α出现偏移[17]，采用式(3)修正

(3)式中，α0、Δα为触发角指令值、端电压自然换相点超前于工频电压正序分量自然换相点的角度。根据线电压过零点计算自然换相点的相位，采用以下方程得到相角δ和δ′，则自然换相点超前角度Δα=δ-δ′。

(4)

图2中利用交流电压和电压开关函数的乘积，得到整流装置的直流电压。考虑到实际中变压器绕组漏感的存在，晶闸管换相过程不能瞬间完成，须计及换相重叠角修正三相整流桥开关函数[14]。则整流桥Ⅰ和Ⅱ的电压开关函数Su1abc和Su2abc为

(5)

其中

(6)

(7)

利用直流侧电压和负载阻抗得到直流电流后(图2)，将直流电流与整流装置的电流开关函数相乘可计算其交流侧电流。整流桥Ⅰ和Ⅱ的电流开关函数Si1abc和Si2abc与式(5)电压开关函数表达式基本相同，仅需将换相修正系数Cn和相位Dn替换

(8)

串联型12脉波整流的直流侧电压udc由整流桥Ⅰ和Ⅱ的直流电压u1dc、u2dc叠加而成

udc(t)=u1dc(t)+u2dc(t)=

u1a(t)Su1a(t)+u1b(t)Su1b(t)+u1c(t)Su1c(t)+

u2a(t)Su2a(t)+u2b(t)Su2b(t)+u2c(t)Su2c(t)

(9)

式(9)中udc除了直流分量外，还有高次电压谐波产生的波动分量，采用频域法计算不同频率udc分量在等效负载上产生的直流电流idc各次频率相量

(10)

式中，n=1，12，24，…，即udc含有12脉波动分量；Udcn、φn分别为第n次直流电压谐波有效值和相位，在计算直流电流时，负载阻抗需加上导通回路的变压器漏抗。将式(10)不同频率分量的直流电流叠加，得到直流电流的时域表达式idc(t)。再将直流电流乘以各相电流开关函数，计算整流桥Ⅰ和Ⅱ的交流侧电流时域表达式i1abc(t)、i2abc(t)，两者合并可得12脉波整流的交流电流时域表达式ia(t)(以a相为例)

(11)

由于整流桥Ⅱ对应的变压器为Y/Δ联结，其交流电流除了经变压器电压比变换外，还存在相位偏移，因而其在一次侧的a相电流与整流桥Ⅱ的交流侧a相和b相电流之差呈正比。对于12脉波整流装置的其他两相电流，可采用类似方式推导得到。

2 不平衡电压下串联型12脉波整流频域谐波模型

2.1 正序电压下12脉波整流谐波耦合导纳矩阵

将整流桥Ⅰ和Ⅱ端电压式(1)和式(2)的正序分量部分，代入a相电流相关计算式(9)～式(11)，并将ia(t)的各次谐波分解，可得仅有正序电压作用下装置交流电流谐波与端电压谐波的矩阵关系

I+=Y+U++Y+*U+*

(12)

式中，I+为交流侧正序谐波电流矢量；U+和U+*为输入正序谐波电压及其共轭矢量；Y+和Y+*为正序电压下的谐波耦合导纳矩阵。式(12)表达式为

(13)

式中，k=1，11，13，…；k为正序电压作用下的整流装置电流谐波次数，h为端电压谐波次数，h=1，5，7，…；K和H分别为最高的电流和电压谐波次数。正序谐波耦合导纳矩阵元素见附录A。

2.2 负序电压下12脉波整流谐波耦合导纳矩阵

将式(1)和式(2)的电压负序分量部分代入a相电流相关式(9)～式(11)，同样可得负序电压作用下电流谐波与端电压谐波的矩阵关系

I-=Y-U-+Y-*U-*

(14)

式中，I-为负序谐波电流矢量；U-和U-*为输入的负序谐波电压及共轭矢量；Y-和Y-*为负序电压下的谐波耦合导纳矩阵，其具体表达式为

(15)

式中，k为负序电压作用下的电流谐波次数，k=1，3，9，11，13，…。与式(13)相比增加了3，9，15，21，…次电流谐波。负序谐波耦合导纳矩阵元素见附录B。

2.3 串联型12脉波整流装置频域谐波模型

(16)

式(16)为串联型12脉波整流的频域谐波模型，该模型综合了不平衡电压下端电压正序和负序分量的共同作用，计及整流装置交流侧谐波电压与电流间耦合关系，将谐波电流与电压的时域非线性特征转换成线性矩阵形式。当直流负载固定时，式(16)导纳矩阵元素仅与触发角和工频电压正序分量初相位有关，简化了其输出电流各次谐波计算的复杂性。

3 实验验证

利用本文建立的频域谐波模型计算串联型12脉波整流装置在不同运行工况下的a相电流及其幅值和相位，与实验测试结果进行对比，验证该频域谐波模型的有效性。搭建图3的串联型12脉波整流装置测试平台，包含三相可编程交流电源、12脉波整流模块、触发脉冲模块和隔离变压器等。采用两个联结方式分别为Y/Y和Y/Δ的双绕组隔离变压器，一次额定电压380 V、kT=1和额定容量3 kV·A。

图3 串联型12脉波整流装置实验平台Fig.3 Experimental setup of series 12-pulse rectifier

表1 12脉波整流装置实验参数Tab.1 Experiment parameters of 12-pulse rectifier

图4 串联型12脉波整流谐波耦合导纳矩阵元素Fig.4 Harmonically coupled admittance matrix elements of series 12-pulse rectifier

图5 案例1整流装置电流波形比较Fig.5 Current waveforms comparison of rectifier under case 1

图6 案例2整流装置电流波形比较Fig.6 Current waveforms comparison of rectifier under case 2

利用12脉波整流的谐波耦合导纳矩阵，与端电压谐波矢量相乘即可计算其输出的各次谐波电流。图5和图6显示了不同运行工况下，12脉波整流装置一次电流ia(t)实测和计算波形。由于变压器联结方式的差异，整流桥Ⅰ电流超前于整流桥Ⅱ电流30°，经两个整流桥串联组成的12脉波整流装置后，交流电流ia(t)的波形呈阶梯状变化。图5a和图6a中端电压负序分量的比例较小，采用本文的谐波模型计算时，同时考虑正序、负序电压作用的Y+Y*和仅考虑正序作用的Y++Y+*电流计算值均与仿真结果吻合。而当端电压负序分量不平衡度为0.2时(图5b、图6b)，仅有电流正序分量的计算结果存在显著误差，因此需采用计及负序电压激励的频域谐波模型计算12脉波整流装置的交流电流。

不同运行工况的12脉波整流电流ia(t)的幅值和相位实验与计算值，如图7和图8所示。图7a或图8a中负序电压分量较小，装置输出电流主要含12k±1次谐波(还有小幅3次谐波)，各次谐波电流幅值随着谐波次数的增加而减小。当整流装置端电压负序分量比例增大后，由于负序电压作用，由图7b或图8b可知，12脉波整流装置电流ia(t)中12k±3次谐波，特别是3、9次谐波显著增大，这与第2.2节的结论一致；但仅考虑正序分量的谐波计算结果，无法得到负序电压下的12k±3次电流谐波。

图7 案例1下整流装置电流频谱Fig.7 Current spectrums of rectifier under case 1

图8 案例2下整流装置电流频谱Fig.8 Current spectrums of rectifier under case 2

为定量分析本文计及负序作用的12脉波整流模型计算与实验结果差异，图7和图8还给出了整流装置输出电流的12k±1和12k±3次谐波实验和Y+Y*模型计算误差百分比，其中电流幅值采用相对误差(以实验值为基准)，相位采用绝对误差。根据图7和图8中4种工况的计算误差可知，在不同电压畸变率与不平衡度情况下，计及负序电压作用的12脉波整流谐波模型计算值与实验结果误差很小，保持在可接受范围内[22]，由此验证该模型的正确性。

根据表1中运行工况，采用文献[13]的误差指标定量分析本文Y+Y*和Y++Y+*模型计算误差随不平衡度和触发角变化规律，如图9所示。随着电压不平衡度增大，整流装置交流电流3、9次谐波含量增加，

而仅考虑正序分量的谐波模型Y++Y+*忽略了12k±3次谐波的作用，导致相同不平衡度下采用Y++Y+*模型的计算误差相对较大，且不平衡度越大，模型误差越大。此外，由图9a知，本文提出的12脉波整流装置模型计算误差随电压畸变率的增加而增加，但仍保持在很小的误差水平。图9b中触发角从0°变化到90°时，整流装置端电压谐波与电流谐波之间的耦合作用增强，同时交流侧电流基波分量减小，导致Y++Y+*模型计算误差增大，但整个触发角变化过程中，本文计及负序电压作用的Y+Y*模型计算误差始终低于10%，模型准确度较高。

图9 整流装置模型误差随不平衡度和触发角变化特性Fig.9 Calculation error of rectification model changing with unbalance degree and firing angle

4 结论

本文建立了串联型12脉波整流装置在电压不平衡下的频域谐波解析模型，通过实验测试，验证该模型能有效计算不同端电压条件下整流器注入电网的谐波电流，具有较高准确度。本文的谐波模型耦合了整流装置机端各次谐波电压和电流，将时域非线性特征转换成频域线性矩阵，实现谐波电流解析计算。该模型可用于高压直流输电、大功率工业整流负荷谐波分析，以指导工程实际中整流设备参数选择；还可用于整流装置接入电网的谐波潮流计算，以实现滤波设备选型和新型谐波抑制措施设计。

附录 A

正序谐波耦合导纳矩阵元素为

(A1)

(A2)

(A3)

当式(A1)中n含0时，x=12n+h；当n中不含0时，x=12n-h；而f(n，k，h)中y即为式(A1)分母的k±12n项，其正负号与对应矩阵元素的分母k±12n项一致。

附录 B

负序谐波耦合导纳矩阵元素为

(B1)

[1] Singh B，Gairola S，Singh B N，et al.Multi-pulse AC-DC converters for improving power quality：a review[J].IEEE Transactions on Power Electronics，2008，23(1)：260-281.

[2] 马俊民，黄永瑞，何青连.800 kV特高压直流输电系统谐波研究[J].电力系统保护与控制，2013，41(21)：33-37. Ma Junmin，Huang Yongrui，He Qinglian.Research on harmonics of±800 kV ultra high voltage direct current transmission system[J].Power System Protection and Control，2013，41(21)：33-37.

[3] 张俊，李跃婷.直流输电工程换流阀控制系统对比分析[J].电力系统保护与控制，2014，42(20)：146-149. Zhang Jun，Li Yueting.Relative analysis for valve control system in HVDC[J].Power System Protection and Control，2014，42(20)：146-149.

[4] 王文，罗安，徐先勇，等.有源滤波器双滞环空间矢量离散控制方法[J].中国电机工程学报，2013，33(12)：10-17. Wang Wen，Luo An，Xu Xianyong，et al.A dual-hysteresis space-vector discrete control method for active power filters[J].Proceedings of the CSEE，2013，33(12)：10-17.

[5] Young C，Wu S，Yeh W，et al.A DC-side current injection method for improving AC line condition applied in the 18-pulse converter system[J].IEEE Transactions on Power Electronics，2014，29(1)：99-109.

[6] 孟凡刚，杨威，杨世彦.并联型12脉波整流系统直流侧有源谐波抑制研究[J].中国科学：技术科学，2011，41(12)：1628-1639. Meng Fangang，Yang Wei，Yang Shiyan.Active harmonic suppression of paralleled 12-pulse rectifier at DC side[J].Scientia Sinica Technologica，2011，41(12)：1628-1639.

[7] 周俊，郭剑波，胡涛，等.高压直流输电系统数字物理动态仿真[J].电工技术学报，2012，27(5)：221-228. Zhou Jun，Guo Jianbo，Hu Tao，et al.Digital/analog dynamic simulation for ±500 kV HVDC transmission system[J].Transactions of China Electrotechnical Society，2012，27(5)：221-228.

[8] 余涛，史军，任震.交直流并联输电系统的间谐波研究[J].中国电机工程学报，2008，28(22)：118-123. Yu Tao，Shi Jun，Ren Zhen.Interharmonic in AC/DC hybrid transmission system[J].Proceedings of the CSEE，2008，28(22)：118-123.

[9] 宁志毫，罗隆福，李勇，等.大功率整流系统谐波功率特性及其对电能计量的影响和节能分析[J].电工技术学报，2012，27(11)：248-255. Ning Zhihao，Luo Longfu，Li Yong，et al.Analysis of energy saving and harmonic power characteristics and its effects on electric energy measurement in high power rectifier system[J].Transactions of China Electrotechnical Society，2012，27(11)：248-255.

[10]乔小敏，王增平，文俊.高压直流输电中谐波对换流变压器差动保护的影响[J].电力系统保护与控制，2009，37(10)：111-114. Qiao Xiaomin，Wang Zengping，Wen Jun.Influence of converter transformer differential protection by harmonic in HVDC transmission system[J].Power System Protection and Control，2009，37(10)：111-114.

[11]薛英林，徐政，黄莹，等.直流输电系统交流侧谐波电流计算的改进时域分段法[J].中国电机工程学报，2010，30(31)：92-99. Xue Yinglin，Xu Zheng，Huang Ying，et al.Improved time domain piecewise calculating method for AC side harmonic current of HVDC systems[J].Proceedings of the CSEE，2010，30(31)：92-99.

[12]Bing Zhonghui，Sun Jian.Frequency-domain modeling of multipulse converters by double-Fourier series method[J].IEEE Transactions on Power Electronics，2011，26(12)：3804-3809.

[13]孙媛媛，尹志明，郑伟杰，等.晶闸管可控电抗器的谐波产生特性研究[J].电工技术学报，2012，27(7)：267-273. Sun Yuanyuan，Yin Zhiming，Zheng Weijie，et al.Study of the harmonic producing characteristics of the thyristor controlled reactors[J].Transactions of China Electrotechnical Society，2012，27(7)：267-273.

[14]Sun Y，Zhang G，Xu W，et al.A harmonically coupled admittance matrix model for AC/DC converters[J]. IEEE Transactions on Power Systems，2007，22(4)：1574-1582.

[15]钟庆，黄凯，王钢，等.不对称三相电压下电压源型换流器谐波分析与抑制策略[J].电力系统自动化，2014，38(4)：79-85. Zhong Qing，Huang Kai，Wang Gang，et al.Harmonic analysis and elimination strategy for voltage source converter under unbalanced three-phase voltage[J].Automation of Electric Power Systems，2014，38(4)：79-85.

[16]孙媛媛，王小宇，尹志明.多谐波源系统的非迭代式谐波潮流分析[J].中国电机工程学报，2012，32(7)：83-90. Sun Yuanyuan，Wang Xiaoyu，Yin Zhiming.Non-iterative harmonic power flow analysis for power systems with multiple harmonic sources[J].Proceedings of the CSEE，2012，32(7)：83-90.

[17]李志铿，王钢，李海峰，等.交流不对称情况下交直流系统谐波分析计算方法[J].电力系统自动化，2010，34(6)：42-47. Li Zhikeng，Wang Gang，Li Haifeng，et al.An analysis and calculation method of harmonic interaction between AC and DC system under asymmetric operation conditions[J].Automation of Electric Power Systems，2010，34(6)：42-47.

[18]高蕾.多相整流变压器输出电压不平衡及其影响的研究[D].哈尔滨：哈尔滨工业大学，2012.

[19]Hu L，Morrison R E.The use of modulation theory to calculate the harmonic distortion in HVDC systems operating on an unbalanced supply[J].IEEE Transactions on Power Systems，1997，12(2)：973-980.

[20]GB/T 15543—1995.电能质量三相电压允许不平衡度[S].

[21]孙媛媛，王小宇，尹志明.三相整流装置谐波产生机理分析及简化模型[J].电力系统及其自动化，2012，36(7)：51-56. Sun Yuanyuan，Wang Xiaoyu，Yin Zhiming.Harmonic characteristics of AC/DC converters and their simplified models[J].Automaiton of Electric Power Systems，2012，36(7)：51-56.

[22]Yong J，Chen L，Chen S.Modeling of home appliances for power distribution system harmonic analysis[J].IEEE Transactions on Power Delivery，2010，25(4)：3147-3155.

Frequency-Domain Harmonic Modeling of the Series 12-pulse Rectifier Under Unbalanced Voltage Condition

WangJiajiaZhouNianchengWangQianggangWeiNengqiao

(State Key Laboratory of Power Transmission Equipment & System Security and New Technology Chongqing University Chongqing 400044 China)

Concerning the series 12-pulse rectifier which is widely used in the high-voltage direct current transmission or the high power rectifying industries，this paper analyzes its operation principle of the equivalent rectification circuit.On this basis，the harmonically coupled admittance matrices of the 12-pulse rectifier under the effect of the positive sequence and the negative sequence voltage are respectively derived，which considers the triggering angle offset caused by the unbalanced voltage condition as well as the commutation overlap angle of the thyristor-controlled rectifying circuit.The harmonically coupled admittance matrix model of the 12-pulse rectifier under unbalanced voltage condition is further established.This model can be used to calculate the harmonic current of the rectifying device analytically.It has the advantage of no need for iteration.Then the experimental platform for the 12 pulse rectifier is set up，the distribution characteristics of the coupled harmonic admittance matrix elements are analyzed，and the accuracy of the rectification model varying with the voltage distortion rate，the unbalance degree，and the firing angle is discussed in this paper.Finally，the efficacy of the proposed frequency-domain analytical model is verified by the comparison between the calculation and the experiment.

12-pulse rectification，unbalanced voltage，harmonic model，commutation overlap angle，harmonically coupled admittance matrix

国家自然科学基金(51277184)资助项目。

2014-11-19 改稿日期2014-12-30

TM46

王佳佳 女，1989年生，硕士研究生，研究方向为电力系统自动化和电能质量。

周念成 男，1969年生，教授，博士，研究方向为电力系统自动化和电能质量。(通信作者)