考虑风电与用户满意度的电动汽车两层智能充放电策略

黄贵鸿 雷 霞 杨 毅 王宇哲 陈晓盛

(电力电子节能技术与装备重点实验室(西华大学) 成都 610039)



考虑风电与用户满意度的电动汽车两层智能充放电策略

黄贵鸿 雷 霞 杨 毅 王宇哲 陈晓盛

(电力电子节能技术与装备重点实验室(西华大学) 成都 610039)

大规模的电动汽车充放电调度问题既关系到电网的安全稳定运行，又关系到运营商的经济利益和用户的使用感受。引入分层分区调度的理念，构建了基于双层规划的电动汽车两层智能充放电模型，并以IEEE16节点标准测试系统数据参数为基础，通过粒子群算法和顺序选择法在Matlab中完成了仿真验证。在上层模型中，通过优化各管辖区在各时段的总充放电功率，保证了运营商利润的最大化，并合理地规避了充放电行为对电网的影响；在下层模型中，通过优化各管辖区内电动汽车的具体充放电策略，使得下层的调度策略与上层的区域总充放电功率尽可能保持一致，并合理地兼顾用户满意度。最后，通过上下层之间的数据交互，实现运营商、电网和用户三者之间利益的有机协调。

电动汽车 分层分区调度 双层规划 粒子群算法 用户满意度

0 引言

随着能源危机、环境污染和全球气候变暖等趋势的加剧，以电能这种清洁能源作为“燃料”的电动汽车拥有广阔的市场前景[1-3]。然而在不久的将来，大量电动汽车接入电网，如果不对其充放电行为加以优化控制，必然会给现有电网的安全与稳定带来严重影响[4-6]。

无论是在电动汽车的推广阶段还是普及阶段，追求利润的最大化都是运营商考虑得最多的问题，同时也是国内外学者研究的热点问题[7-9]。文献[8]以充电站运营收益最大化为目标，以配电变压器容量及最大限度满足用户充电需求为约束条件，建立了充电站内电动汽车有序充电的数学模型；文献[9]提出的有序充放电策略考虑了电动汽车充放电与风力发电在平抑负荷波动、减小峰谷差、降低网损等方面的互补效应；文献[10]提出了一种电力市场环境下的电动汽车调度方法，通过选择电价较低时段充电和向系统提供调频或旋转备用，以使电动汽车的总充电成本最小化；文献[11]建立了以负荷峰谷差最小化为优化目标的计及用户行驶习惯的插电式混合动力汽车智能充电模型，并对各时段PHEV的反向放电能力进行估算；文献[12]根据电动汽车充电特性建立了电动汽车充电负荷模型，实现了平滑电网等效负荷波动的目的；文献[13]提出了以换电站充电功率为控制对象的有序充电调度策略，有效减小了电网峰谷差，提高了负荷率，起到平稳负荷波动的作用；文献[14]以电动公交车为研究对象分析其营运特点和充放电行为，同时在基于电池租赁的商业模式下，研究电动公交车的V2G放电能力，通过模拟集中充电站的运营情况，建立了集中充电、放电组合策略优化模型；文献[15]引入了对电动汽车进行分层分区调度的理念，构建了基于双层优化的可入网电动汽车充放电调度模型。在上层模型中，通过优化各电动汽车代理商在各时段的调度计划，使系统在研究时间区间内总负荷水平的方差最小化，从而实现削峰填谷；在下层模型中，通过各电动汽车代理商对其所管辖电动汽车充放电时间的优化管理，以便与上层的调度计划尽可能一致。

现有的电动汽车有序充放电策略仅考虑了问题的某一个方面，或仅从问题的某一个方面出发进行相对孤立的探讨。首先，现有的有序充放电策略并未实现电网、运营商、用户三者之间有机的协调；其次，现有的有序充放电策略并未充分利用电动汽车充放电与风力发电之间互补协调调度的经济效应；最后，现有的有序充放电策略并未充分考虑到未来V2G的发展趋势[16]。此外，在现有的有序充放电策略中，电动汽车运营商为了实现自身利益的最大化，可能会忽略用户的满意度。本文在现有的有序充电策略的基础上，引入风力发电，提出了同时兼顾电动汽车运营商、电网和用户利益的电动汽车智能充放电策略。

本文采用指定功率充放电模式，电动汽车具有额定的充放电功率，这决定了电动汽车充放电调度是一个离散的整数型优化问题。具体到每一辆电动汽车，充放电功率即额定充放电功率，不存在任何其他数值。运营商需要协调的，就是在一天中的24个时段内，各电动汽车最优的充放电时段。考虑到未来电动汽车用户数量会呈现出显著增长的趋势，为了实现最优化调度，电动汽车运营商每天需要处理的数据量会非常庞大，如果依然采用现有的单层调度模式，无法实现决策的快速性和准确性。因此，本文提出了电动汽车两层智能充放电策略，旨在实现电动汽车运营商利润的最大化，保证现有城市配电网安全、稳定地运行，并尽可能地考虑到用户的满意度，最终保障电动汽车运营商持续、健康、稳定地运营。本文通过上层模型中的目标函数体现了运营商的利益，并通过约束条件，从安全性角度保证了电网的利益；在下层模型中，从用户的行驶习惯和充/放电需求的角度，考虑了用户的充放电满意度；最后通过上下层交互，尽可能地使用户的总体利益与运营商的利益在不断博弈的过程中实现平衡，而在此过程中，电网的利益将始终得以满足。

1 两层优化调度模型

1.1 背景介绍

本文假设我国某个城市中的某电动汽车运营商共有M辆电动汽车需要调度，每一辆电动汽车都具有相同的电气参数，即相同的额定容量、额定充/放电功率等，且严格服从电动汽车运营商的调度安排。现将电动汽车运营商所属的M辆电动汽车根据电气位置、地理位置等模糊特征进行归类，并平均拆分为X个充电管辖区。这样，每个充电管辖区内具有N辆电动汽车，计算量也随之相应减小。

假设电动汽车运营商拥有自营的风电场，风机出力以预测值为准[17-20]，且通过独立输电线路直接服务于电动汽车用户的充电。在一天中的某一个时段内，当用户净充放电总量(充电总量与放电总量之差)大于运营商自营风机出力时，运营商需要向电网购电；反之，运营商可向电网售电。无论是以上哪一种情况，电动汽车运营商均可通过与电网和与用户之间的购售电价差实现盈利。

在此控制过程中，运营商在保证自身利益的同时，需要制定满足电网安全性约束的各区域宏观充放电功率。并在此基础上，结合用户的使用感受，制定具体到每个用户(集群)的实际充放电调度功率。

1.2 控制流程

多层规划概念最早是由J.Bracken和J.T.McGill[21]于1973年提出的，用以解决多层规划与优化问题，其中双层规划是多层规划的特例。顾名思义，双层规划包括上下两层，上层决策结果一般会影响下层目标和约束条件，而下层则将决策结果反馈给上层，从而实现上下层决策的相互作用[15]。

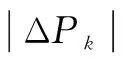
图1 两层优化控制流程Fig.1 Two-layer optimization control flow

2 区域层优化模型

2.1 目标函数

在区域层中，电动汽车充放电运营商以自身利润最大化为控制目标，以不影响现有城市配电网安全运行为约束条件，通过粒子群智能优化算法，得到各充电管辖区在一天中24时段的最优区域总充放电功率Pk，t。区域层目标函数如式(1)所示。

(1)

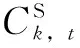
(2)

式(1)中，(Pk，t-βkPw，t)为考虑风机出力的电动汽车运营商旗下第k个充电管辖区在t时刻的对外总充放电功率。若Pk，t-βkPw，t>0，则表示该辖区所配给的风电额度不足以提供辖区内所用用户的充电需求，此时运营商需要向电网购电；若Pk，t-βkPw，t<0，则表示该辖区所配给的风电额度足以提供辖区内所用用户的充电需求，且还有结余，此时运营商可向电网售电。

2.2 风电单位折算成本

电动汽车运营商旗下拥有自营风力发电场，该风电场通过专用输电导线与各充电管辖区相连。在本文中，风电场出力必须优先满足用户充电需要，若有剩余，可向电网反送电。假设风力发电机组使用寿命为20 a，考虑建设成本、维修费用、人力成本、物价上涨指数、政府补贴，电动汽车运营商自营风场的风电单位折算成本可通过式(3)得到[22，23]。

(3)

式中f(Y)可通过式(4)得到

f(Y)=(1+βCPI)Y-1[Cwage+(1+∂m)Y-1Crepair]

(4)

式中，Cbuild为单台风机建设成本；Nw为风机数量；βCPI为物价上涨系数；Cwage为年化人力成本；Crepair为年化维修成本；∂m为风电场年化故障增长率；Bsubsidy为国家节能减排补贴。

2.3 约束条件

1)多时段潮流约束

(5)

且

(6)

式(5)、式(6)中

PEi,t=Pk,t-βkPw,t

(7)

式中，PDi，t、QDi，t分别为电动汽车、风机接入前，t时刻节点i接入的基础负荷有功功率和无功功率；node表示节点总数；PEi，t为考虑风机出力的电动汽车运营商旗下第k个充电管辖区在t时刻的对外充放电功率，且辖区k与节点i相连；Ui，t为节点i在t时刻的电压幅值；θij，t为节点i、j在t时刻的电压相角差；Gij与Bij分别为连接节点i与j之间支路的电导和电纳。

2)风电配额约束

(8)

3)风电机组出力约束

(9)

4)节点电压偏移量约束

ΔUi,t≤5%

(10)

式中，ΔUi，t为节点i在t时刻的电压偏移百分比。

5)线路潮流约束

(11)

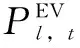
6)支路损耗约束

(12)

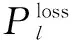
7)峰谷差约束

(13)

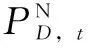
(14)

8)负荷率约束

(15)

9)负荷标准差约束

(16)

10)各充放电管辖区在时段t的调度约束

NkavPcharge≥Pk,t≥kSNkavPdischarge

(17)

式中，N为每个辖区所需调度的电动汽车数量；Pcharge为电动汽车额定充电功率；Pdischarge为电动汽车额定放电功率；kav为可用系数，由于所有电动汽车同时充电或同时放电的可能性几乎为零，各辖区的实际总充放电功率必然小于该时段内电动汽车数量与额定充放电功率的乘积；kS为参与V2G的电动汽车数量占所有电动汽车总量的比值。

3 用户层优化模型

3.1 目标函数

用户层中，电动汽车充放电运营商以实际调度结果与区域层参考数据偏差的绝对值最小为目标，并充分考虑用户的充放电需要，通过顺序选择法，得到每辆电动汽车的最优充放电策略。然后根据前面所提到的数据返回原则，选择性地将实际调度结果与区域层参考数据的偏差返回到区域层。用户层目标函数如式(18)所示。

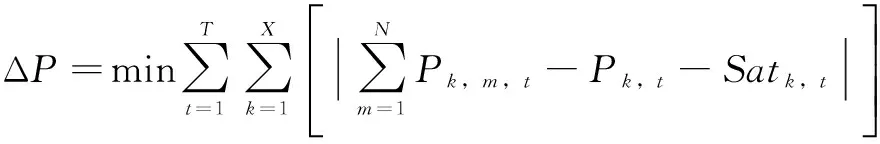
(18)

式中，Pk，m，t为辖区k中第m辆电动汽车在t时刻的充放电功率。每辆电动汽车都具有额定的充放电功率，当辖区m内第k辆电动汽车在t时刻充电时，Pk，m，t=Pcharge；当辖区m内第k辆电动汽车在t时刻放电时，Pk，m，t=Pdischarge。因此，用户层控制变量Pk，m，t是一个只对时间t进行求解的一维未知变量；Satk，t表示用户满意度矩阵Sat第k行、第t列中的元素。满意度矩阵Sat是描述用户充放电行为的X×T维修正矩阵。

3.2 返回数据

本文将上下层最大交互次数设置为L，对于第kk次交互，若满足返回数据的条件，则返回数据

(19)

即式(2)。因此，区域层目标函数(1)可改写成如下形式

(20)

3.3 约束条件

1)电动汽车蓄电池充放电约束

(21)

式中，Sk，m，t为辖区k中第m辆电动汽车在t时刻的电池电量；ηch为充电效率；ηdch为放电效率。

2)蓄电池安全性约束

Smin≤Sk,m,t≤Smax

(22)

3)次日行驶需要约束

Sk,m,tk,m,d≥Srequire

(23)

式中，tk，m，d为辖区k中第m辆电动汽车的充电结束时间。

4)不可调度时段约束

Pk,m,t=0 (当ttk,m,d时)

(24)

式中，tk，m，a为辖区k中第m辆电动汽车的充电开始时间。

5)充/放电连续性约束

Pk,m,tk,m,a×Pk,m,tk,m,a+1×…×Pk,m,tk,m,d-1×Pk,m,tk,m,d≠0

(25)

且

Pk,m,tk,m,da×Pk,m,tk,m,da+1×…×Pk,m,tk,m,dd-1×Pk,m,tk,m,dd≠0

(26)

式中，tk，m，da为辖区k中第m辆电动汽车的放电开始时间；tk，m，dd为辖区k中第m辆电动汽车的放电结束时间。

6)不可同时充放电约束

tk,m,da≥tk,m,d+3

(27)

根据此约束条件，从充电结束时刻算起，电动汽车必须在2h后才能开始放电，既保证了电池的使用寿命，降低了使用成本，又符合常理。

4 仿真设置

4.1 基础数据

本文是在IEEE16节点接线方式、线路参数等基础上进行仿真的。图2中，数字表示节点序号，带“#”数字表示线路序号。三角形节点按升序分别接入电动汽车运营商旗下的第X个辖区。运营商自营风电场通过专用输电线路直接与各充放电管辖区相连。

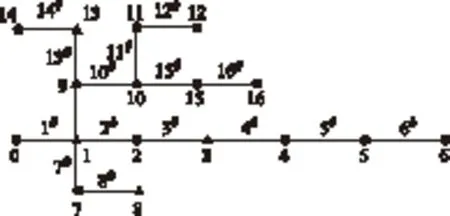
图2 IEEE16节点接线图Fig.2 IEEE16 node connection diagram

假设我国某个城市中的某电动汽车充放电运营商共有2 400辆电动汽车需要调度，该运营商旗下拥有6个充放电管辖区，每个充放电管辖区管辖400辆电动汽车的充放电行为。

为降低用户层计算维度，提高计算速度，现将每个充电管辖区内的400辆电动汽车分为40个充放电集群，每个集群具有10辆充放电行为完全相同的电动汽车。这样，计算维度也就从之前的400×24降低到40×24。

本文假设进行50次区域层与用户层的数据交互。其中，区域层将向用户层传送51次基准数据，用户层将向区域层返回50次修正数据。

运营商自营风电场风电机组出力值Pw，t直接引用了文献[17-20]中的风电出力预测值。在一天中的24个时段，风电机组的出力如表1所示。

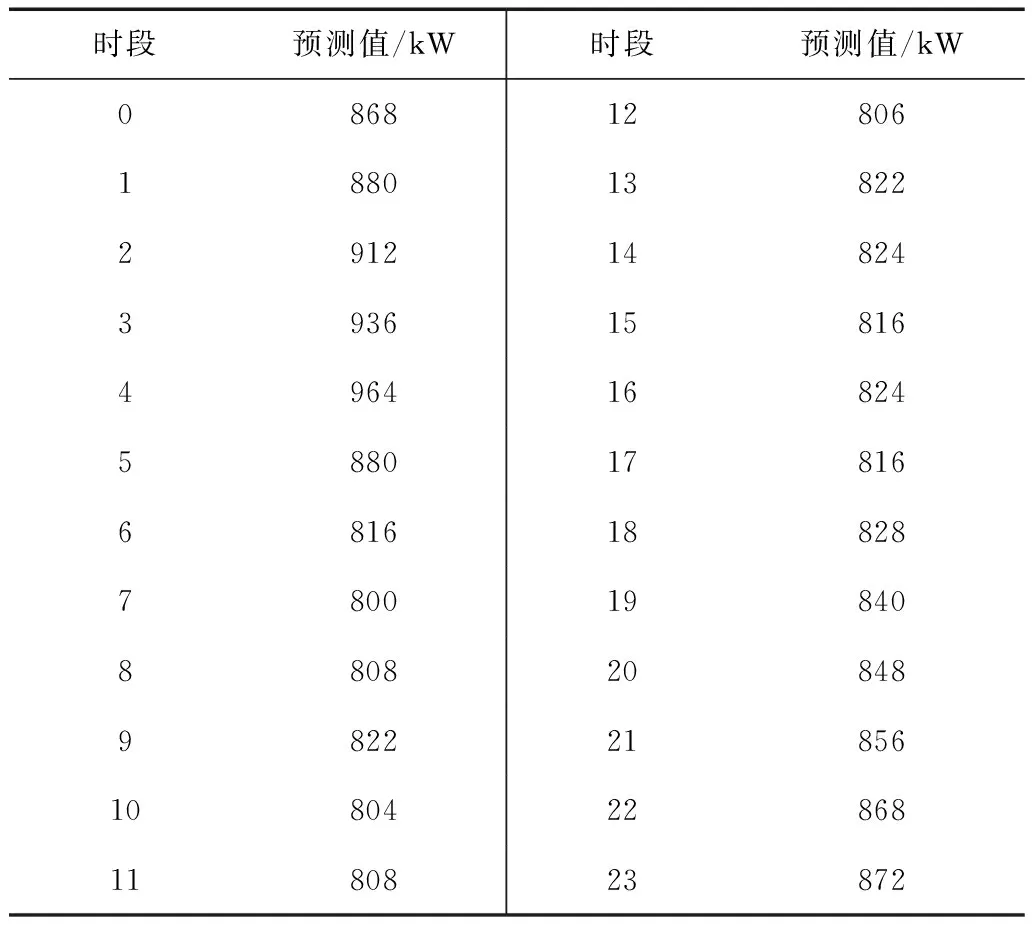
表1 风电机组出力预测值Tab.1 Predicted value of wind turbine operator set output

电动汽车运营商旗下6个充电管辖区所获得的风电配额，可根据风机地理位置、输电线路成本、配电网络特性等实际情况进行适当选取。本文以6个充电管辖区分别获得0.1、0.2、0.25、0.28、0.12和0.05的风电配额为例进行仿真计算。

本文仿真所采用的基础负荷曲线直接引用了文献[24-26]中的数据。在一天中的24个时段，基础负荷如表2所示。

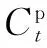
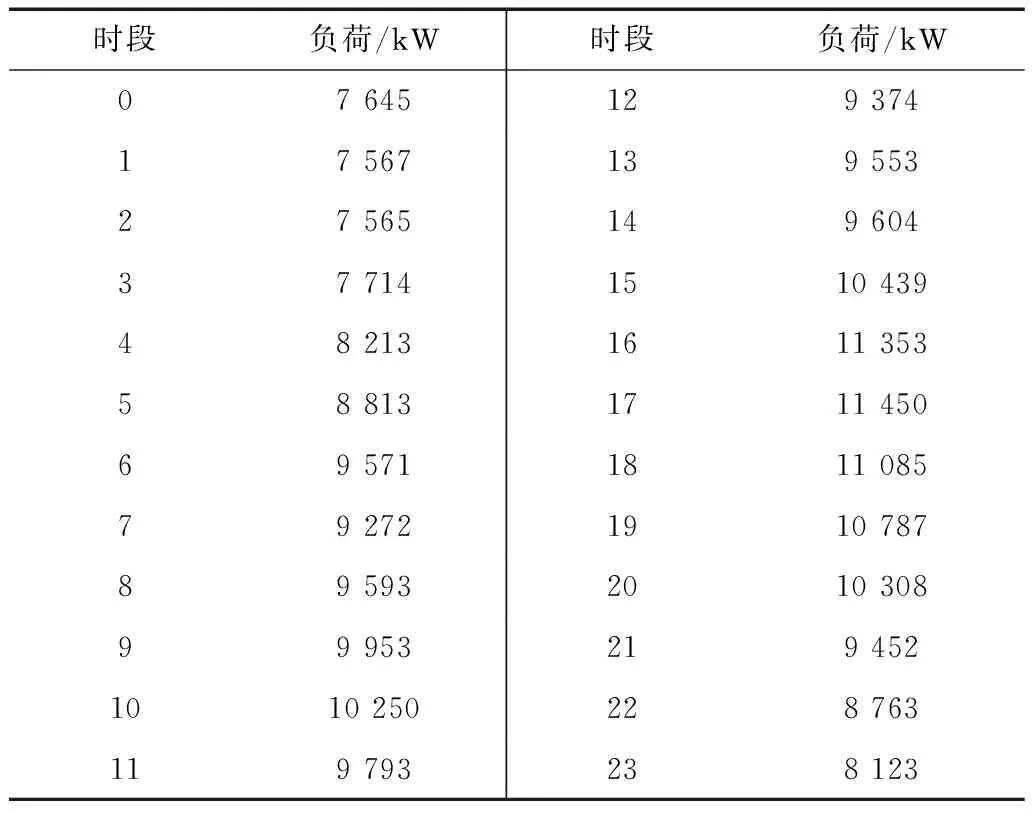
表2 基础负荷Tab.2 Original load

文献[26]中某地区高负荷率电价的基础上，根据本文实际需要，做了适当修改。后者在低负荷率电价的基础上[26]，根据本文实际需要，做了适当修改，制定了运营商与辖区一用户之间的分时电价。其余充放电管辖区由于所处的地理位置、电气位置不同，以辖区一为基准，电价有适当不同。其中，对于辖区二、三、四、五、六，运营商与用户之间的电价在辖区一基准电价的基础上，分别高出0.01、0.015、0.03、0.025和0.02元/kWh。运营商与电网之间的分时电价如表3所示。运营商与辖区一用户之间的基准分时电价如表4所示。

表3 运营商与电网之间的分时电价Tab.3 Time-of-used electricity price between provider and grid

表4 运营商与辖区一用户之间的分时电价Tab.4 Time-of-used electricity price between provider and users in district 1

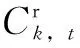
表5 辖区1单位运营维护成本Tab.5 Unit operation and maintenance cost in district 1

为简化计算，本文将电动汽车运营商自营风电场风电单位成本Cw设置为0.35元/kWh。

4.2 充放电时间

假设每辆电动汽车具有相同的电池容量和充放电功率。其中，每辆电动汽车的电池容量为12 kWh，充电功率Pcharge为3 kW，放电功率Pdischarge为-1.5 kW。文献[27，28]对电动汽车用户的行驶习惯和充放电行为进行了建模分析，基于此，为保证第二天的正常使用，本文假设每辆电动汽车充电结束时的SOC(State of Capacity)满足正态分布，其期望值为0.9；充电开始时的SOC亦满足正态分布，其期望值为0.1。每辆电动汽车的充电效率ηch为80%，这样，每辆电动汽车在一天中的连续充电时间TC满足以4 h为期望值的正态分布，如式(28)所示。

(28)

(29)

考虑到电动汽车具有参与放电的V2G行为，参与V2G的电动汽车占所有电动汽车总量的70%。假设参与V2G的电动汽车放电开始时的SOC满足期望值为0.3的正态分布，放电效率ηdch为80%，这样，每辆参与V2G的电动汽车在一天中的连续放电时间TD满足以2 h为期望值的正态分布，如式(30)所示。

(30)

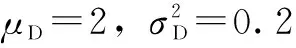
(31)

4.3 粒子群算法

在区域层中，本文采用粒子群智能优化算法进行求解[29]。其中，将优化变量Pk，t作为粒子，初始化粒子在式(17)的约束下随机产生。初始化粒子个数设置为20，迭代次数设置为500。

粒子群算法计算流程：

1)初始化一群规模为20的粒子，每个粒子包括400×24维的随机位置Pk，t和速度Vk，t。

2)评价每个粒子的适应度，即目标函数式(1)的值。

3)对每个粒子，将其适应度值与其目前取得的最好位置(局部最优值)对应的适应度值作比较，如果较好，则将此位置作为当前的局部最好位置pbest。

4)对每个粒子，将其适应度值与群体目前所取得的最好位置(全局最优值)对应的适应度值作比较，如果较好，则将该位置作为当前的全局最好位置gbest。

5)分别根据式(32)、式(33)调整粒子速度和位置。

Vk,t=w×Vk,t+c1×rand()×(pbestk.t-Pk,t)+

c2×rand()×(gbest-Pk,t)

(32)

Pk,t=Pk,t+Vk,t

(33)

6)迭代次数未达到500则转向步骤2)。

4.4 考虑用户满意度的顺序选择法

在用户层中，本文采用顺序选择法进行求解，得到每个电动汽车集群最优的充放电策略，进而得到Pk，m，t。以辖区一为例，通过区域层优化计算得到的区域总充放电功率P1，t具有最大值与最小值。现将P1，t最大值与最小值在一天中出现的最早位置t分别记为tmax和tmin，对于辖区一中的第一个电动汽车集群，将tmax作为其充电开始时间，将tmin作为其放电开始时间；修正P1，t，再一次将修正后的P1，t最大值与最小值在一天中出现的最早位置t分别记为tmax和tmin，对于辖区一中的第二个电动汽车集群，将tmax作为其充电开始时间，将tmin作为其放电开始时间；修正P1，t，以此往复，直到得到辖区一中所有电动汽车集群的充放电功率，进而得到所有电动汽车的充放电功率Pk，m，t。

考虑到用户的实际充放电需要，绝大多数用户希望在夜晚入睡时进行充电，此时的充电电价最低，如表4所示，同时充电也最方便。在文献[27，28]对用户行驶习惯和充放电需求进行建模分析的基础上，本文对用户的充放电行为进行了简化。假设参与V2G的用户均希望在下班回到家后的18∶00和19∶00开始放电，此时电动汽车处于闲置，电价处于峰时电价，获利将会最大。这样，考虑用户满意度后，根据顺序选择法的计算原理，可将用户满意度表示成6×24维矩阵Sat，并假设每个充放电管辖区内用户满意度指标相同，即Sat矩阵每行的行矢量相同。因此，可以将矩阵Sat的第k行以24维行矢量的形式表示成式(34)。

Satk=K[100,100,100,100,100,100,0,0,0,0,

0,0,0,0,0,0,0,-100,-100,0,80,80,80,80]

(34)

式中，K为用户满意度权重，K值越大，该充电策略越偏向于用户的利益。第1列～第6列的数值为100，根据顺序选择法的计算原理，可在很大程度上将用户的充电行为引入到00∶00～05∶00；第18列～第19列的数值为-100，可以在很大程度上将用户的放电行为引入到17∶00～18∶00；第21列～第24列的数值为80，可在一定程度上将用户的充电行为引入到20∶00～23∶00。在用户层中采用顺序选择法进行求解时，可采用矩阵B取代之前的矩阵P(其第k行第t列元素为Pk，t)。矩阵B为区域层总充放电功率矩阵P与用户满意度矩阵Sat之和，即

B=P+Sat

(35)

对于每个充放电管辖区，依次通过顺序选择法，将得到其中每辆电动汽车的充放电策略Pk，m，t。用户层求解最优调度方案的具体流程如图3所示。

图3 用户层优化控制流程Fig.3 User-layer optimization control flow

5 仿真结果

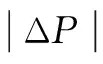
(36)

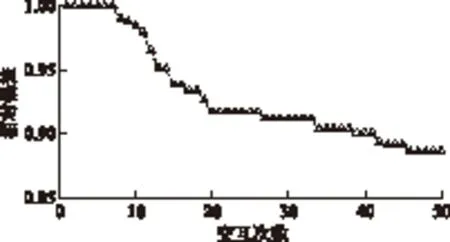
图4 两层优化相对偏差Fig.4 Two-layer optimization relative deviation

根据本文的构想，第46次交互所产生的区域层总充放电功率Pk，t和用户层实际调度功率Pk，m，t即为最优的两层调度方案。

在此最优调度方案下，可认为区域层与用户层能够协同调度，且区域层指标能相对准确地反应用户层的相关指标。因此，以下均从区域层出发，探讨在最优调度方案下，运营商利润、电压偏移量、线路潮流值、支路网损值、峰谷差、负荷率、标准差等指标。

在最优调度方案下，电动汽车运营商所取得的最大利润为2.765万元/d。以辖区一为例，区域层最优总充放电功率Pk，t如图5所示。

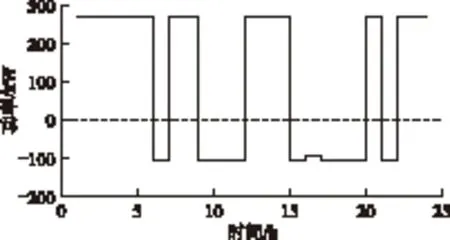
图5 辖区一最优充放电计划Fig.5 Optimumcharge-discharge plan for district 1

由图5可知，充电管辖区对外所表现出的宏观充放电行为符合实际需要，即在晚上进行充电，在下午负荷高峰且汽车闲置时段进行放电。该充放电计划在为运营商赚取高额利润的同时，在很大程度上提高了用户满意度，并合理地避开了负荷高峰。

以辖区一内各电动汽车集群为例，用户层根据基准数据Pk，t得到的每个电动汽车集群充放电策略如表6所示。表6为一个40×24矩阵，表示辖区一内40个电动汽车集群在一天中24个时段的充放电策略。其中，第一列为行序数，表示电动汽车集群序列数；第一行为列序数，表示一天中的时段t。“+”表示充电，“-”表示放电，“空格”表示既不充电也不放电。根据本文假设，对于70%的电动汽车，既有充电计划，也有放电计划；对于30%的电动汽车，只有充电计划，没有放电计划。

表6 辖区一各电动汽车集群充放电策略Tab.6 Charge-discharge tactics for every electric vehicle in district 1

以辖区一为例，区域层与用户层的拟合程度如图6所示。其中，光滑折线为图5中的区域层最优区域总充放电功率Pk，t曲线，三角形折线表示用户层在每个电动汽车集群均实现最优调度方案Pk，m，t的基础上对外的总体表现，即

(37)

图6 辖区一最优充放电计划与调度方案Fig.6 Optimumcharge-discharge plan and scheduling scheme for district 1

由图6可看出，在最优调度方案下，用户层能很好地与区域层实现协同调度。由于考虑了用户满意度指标，在用户层中，夜间总充电功率有所增大，18∶00、19∶00两个时段总放电功率有所增大。

图7表示电动汽车运营商在一天中24个时段内所管辖的所有电动汽车总充放电行为。

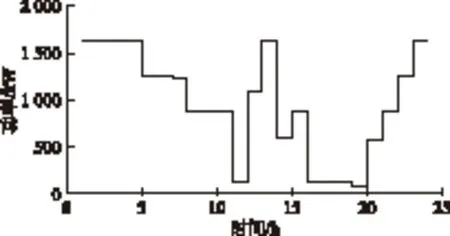
图7 运营商总充放电曲线Fig.7 Gross charge-discharge curve for provider

由图7中运营商总充放电曲线可看出，在任何时段，充电功率始终大于放电功率，因为对于电动汽车用户而言，必然以充电为主，放电为辅。充电主要安排在负荷低谷时段，放电主要安排在负荷高峰时段。

在最优调度方案下，加入电动汽车和风机后的综合负荷曲线与基础负荷曲线如图8所示。

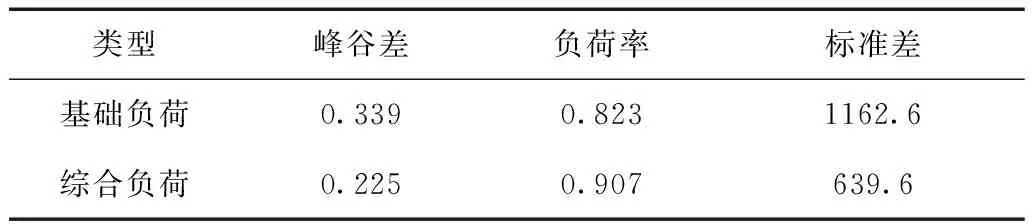
由图8可知，加入电动汽车和风电机组后，如果以本文提出的控制策略加以约束，负荷将会更加平稳，负荷曲线将会更加平滑。该控制策略无论在削峰填谷、平抑负荷波动还是在提高负荷率上，均有非常理想的效果。加入电动汽车和风电机组后的综合负荷在峰谷差、负荷率和标准差上均明显优于基础负荷，且均满足本文所设置的约束条件，其相关指标如表7所示。

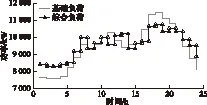
图8 负荷曲线Fig.8 Load curve

类型峰谷差负荷率标准差基础负荷0.3390.8231162.6综合负荷0.2250.907639.6

加入电动汽车与风电机组后，在18∶00和24∶00两个典型时刻，节点电压偏移情况如图9所示。本文采用前推回代法计算节点电压、网络损耗和线路潮流[30]。

图9 节点电压Fig.9 Node voltage

加入电动汽车与风机后，在18∶00和24∶00两个典型时刻，支路网损如图10所示[30]。

图10 支路网损Fig.10 Branch network loss

加入电动汽车与风机后，在18∶00和24∶00两个典型时刻，线路潮流如图11所示[30]。

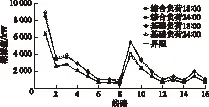
图11 线路潮流Fig.11 Line power flow

由图9～图11可知，无论是在基础负荷的最低谷时段，还是在基础负荷的最高峰时段，电动汽车和风电机组的接入都未造成节点电压、支路网损和线路潮流的越限。在基础负荷的最低谷时段，随着电动汽车和风机的接入，节点电压、支路网损和线路潮流略有所增大；然而在基础负荷的最高峰时段，随着电动汽车和风机的接入，该指标却有所减小。

本文并未考虑电动汽车充放电对配电网的谐波污染[31]。

6 结论

本文在分层分区的框架内，通过区域层与用户层的智能交互，很好地实现了运营商、电网与用户三者之间的有机统一。在运营商侧，实现了运营商利润的最大化；在电网侧，保证了城市配电网的安全稳定运行，并在一定程度上提高了电能质量；在用户侧，通过引导充放电行为的方式，在一定程度上提升了用户的满意度。对电网而言，其利益是一个综合、复杂和系统的问题，然而安全与稳定是电网运行的根本，因此本文主要考虑了电网的安全性约束；对电动汽车用户而言，充放电成本是衡量满意度高低的一个指标，然而充放电时段的合理性同样重要，因此本文主要考虑了用户的行驶习惯。运营商、电网与用户三者之间的有机协调，依然是一个具有深入研究价值的课题。

[1] 张文亮，武斌，李武峰，等.我国纯电动汽车的发展方向及能源供给模式的探讨[J].电网技术，2009，33(4)：1-5. Zhang Wenliang，Wu Bin，Li Wufeng，et al.Discussion on development trend of battery electric vehicles in China and its energy supply mode[J].Power System Technology，2009，33(4)：1-5.

[2] Brooks A，Lu E，Reicher D，et al.Demand dispatch[J].IEEE Power and Energy Magazine，2010，8(3)：20-29.

[3] Andersen P H，Mathews J，Morten R.Integrating private transport into renewable energy policy：the strategy of creating intelligent recharging grids for electric vehicles[J].Energy Policy，2009，37(7)：2481-2486.

[4] Schneider K，Gerkensmeyer C，Kintner-Meyer M，et al.Impact assessment of plug-in hybrid vehicles on Pacific Northwest distribution systems[C].IEEE Power and Energy Society General Meeting on Conversion and Delivery of Electrical Energy in the 21st Century，Pittsburgh，PA，USA，2008：6.

[5] 马玲玲，杨军，付聪，等.电动汽车充放电对电网影响研究综述[J].电力系统保护与控制，2013，41(3)：140-148. Ma Lingling，Yang Jun，Fu Cong，et al.Review on impact of electric car charging and discharging on power grid[J].Power System Protection and Control，2013，41(3)：140-148.

[6] 赵俊华，文福拴，杨爱民，等.电动汽车对电力系统的影响及其调度与控制问题[J].电力系统自动化，2011，35(14)：2-10. Zhao Junhua，Wen Fushuan，Yang Aimin，et al.Impacts of electric vehicles on power systems as well as the associated dispatching and control problem[J].Automation of Electric Power Systems，2011，35(14)：2-10.

[7] 赵俊华，文福拴，薛禹胜，等.计及电动汽车和风电出力不确定性的随机经济调度[J].电力系统自动化，2010，34(20)：22-29. Zhao Junhua，Wen Fushuan，Xue Yusheng，et al.Power system stochastic economic dispatch considering uncertain outputs from plug-in electric vehicles and wind generators[J].Automation of Electric Power Systems，2010，34(20)：22-29.

[8] 徐智威，胡泽春，宋永华，等.充电站内电动汽车有序充电策略[J].电力系统自动化，2012，36(11)：38-43. Xu Zhiwei，Hu Zechun，Song Yonghua，et al.Coordinated charging of plug-in electric vehicles in charging stations[J].Automation of Electric Power Systems，2012，36(11)：38-43.

[9] Song Yonghua，Yang Xia，Lu Zongxiang.Integration of plug-in hybrid and electric vehicles：experience from China[C].Proceedings of IEEE Power and Energy Society General Meeting，Minneapolis，MN，USA，2010：1-6.

[10]Caramanis M，Foster J M.Management of electric vehicle charging to mitigate renewable generation intermittency and distribution network congestion[C].Proceedings of the 48th IEEE Conference on Decision and Control，Shanghai，China，2009：4717-4722.

[11]李高望，钱斌，石东源，等.含插电式混合动力汽车的机组组合问题[J].电网技术，2013，37(1)：32-38. Li Gaowang，Qian Bin，Shi Dongyuan，et al.Unit commitment problem considering plug-in hybrid electric vehicle[J].Power System Technology，2013，37(1)：32-38.

[12]黄润，周鑫，严正，等.计及电动汽车不确定性的有序充电调度策略[J].现代电力，2012，29(3)：57-63. Huang Run，Zhou Xin，Yan Zheng，et al.The controlled charging dispatch strategy by considering of the uncertainty of electric vehicles[J].Modern Electric Power，2012，29(3)：57-63.

[13]田文奇，和敬涵，姜久春，等.电动汽车换电站有序充电调度策略研究[J].电力系统保护与控制，2012，40(21)：114-119. Tian Wenqi，He Jinghan，Jiang Jiuchun，et al.Research on dispatching strategy for coordinated charging of electric vehicle battery swapping station[J].Power System Protection and Control，2012，40(21)：114-119.

[14]郑丹，文福拴.租赁模式下的电动汽车电池集中充放电策略[J].华南理工大学学报(自然科学版)，2013，41(5)：105-111. Zheng Dan，Wen Fushuan.Charging and discharging strategies of batteries of electric vehicles in lease mode[J].Journal of South China University of Technology(Natural Science Edition)，2013，41(5)：105-111.

[15]姚伟锋，赵俊华，文福拴，等.基于双层优化的电动汽车充放电调度策略[J].电力系统自动化，2012，36(11)：30-37. Yao Weifeng，Zhao Junhua，Wen Fushuan，et al.A charging and discharging dispatching strategy for electric vehicles based on Bi-level optimization[J].Automation of Electric Power Systems，2012，36(11)：30-37.

[16]刘晓飞，张千帆，崔淑梅.电动汽车V2G技术综述[J].电工技术学报，2012，27(2)：121-127. Liu Xiaofei，Zhang Qianfan，Cui Shumei.Review of electric vehicle V2G technology[J].Transactions of China Electrotechnical Society，2012，27(2)：121-127.

[17]刘瑞叶，黄磊.基于动态神经网络的风电场输出功率预测[J].电力系统自动化，2012，36(11)：19-22. Liu Ruiye，Huang Lei.Wind power forecasting based on dynamic neural networks[J].Automation of Electric Power Systems，2012，36(11)：19-22.

[18]Costa A，Crespo A，Navarro J，et al.A review on the young history of the wind power short-term prediction[J].Renewable and Sustainable Energy Reviews，2008，12(6)：1725-1744.

[19]杨秀媛，肖洋，陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报，2005，25(11)：1-5. Yang Xiuyuan，Xiao Yang，Chen Shuyong.Wind speed and generated power forecasting in wind farm[J].Proceedings of the CSEE，2005，25(11)：1-5.

[20]葛江北，周明，李庚银.大型风电场建模综述[J].电力系统保护与控制，2013，41(17)：146-153. Ge Jiangbei，Zhou Ming，Li Gengyin.Review on large-scale wind farm modeling[J].Power System Protection and Control，2013，41(17)：146-153.

[21]Bracken J，McGill J T.Mathematical programs with optimization problems in theconstraints[J].Operations Research，1973，21(1)：37-44.

[22]徐丽萍，林俐.基于学习曲线的中国风力发电成本发展趋势分析[J].电力科学与工程，2008，24(3)：1-4. Xu Liping，Lin Li.Study on the cost trends of wind power in china based on the learning curve[J].Electric Power Science and Engineering，2008，24(3)：1-4.

[23]周双喜，王海超，陈寿孙.风力发电运行价值分析[J].电网技术，2006，30(14)：98-102. Zhou Shuangxi，Wang Haichao，Chen Shousun.Analysis on operation value of wind power resources[J].Power System Technology，2006，30(14)：98-102.

[24]赵儆，康重庆，葛睿，等.电力市场中多日负荷曲线的预测[J].电力自动化设备，2002，22(9)：31-33. Zhao Jing，Kang Chongqing，Ge Rui，et al.Multi-day load curve forecasting in electricity market[J].Electric Power Automation Equipment，2002，22(9)：31-33.

[25]肖建华，王锐凤，温春楠，等.典型日负荷曲线预测的一种简单方法[J].吉林电力，2006，34(2)：14-17. Xiao Jianhua，Wang Ruifeng，Wen Chunnan，et al.A simple method of typical day load curve forecasting[J].Jilin Electric Power，2007，34(2)：14-17.

[26]郭联哲，李莉，谭忠富，等.基于模糊需求和用户分类响应程度的分时电价设计模型[J].华东电力，2007，35(5)：12-15. Guo Lianzhe，Li Li，Tan Zhongfu，et al.Time-of-use price design models based on fuzzy demand and users’diverse response[J].East China Electric Power，2007，35(5)：12-15.

[27]刘文霞，张敏，张建华，等.电动汽车负荷对配电网可靠性影响的量化分析[J].电力系统及其自动化学报，2013，25(4)：1-6. Liu Wenxia，Zhang Min，Zhang Jianhua，et al.Reliability modeling and quantitative analysis of distribution network considering electric vehicle charging and discharging[J].Proceedings of the CSU-EPSA，2013，25(4)：1-6.

[28]田立亭，史双龙，贾卓.电动汽车充电功率需求的统计学建模方法[J].电网技术，2010，34(11)：126-130. Tian Liting，Shi Shuanlong，Jia Zhuo.A statistical model for charging power demand of electric vehicles[J].Power System Technology，2010，34(11)：126-130.

[29]李志，陈年生，郭小珊，等.粒子群算法及其改进技术研究[J].湖北师范学院学报(自然科学版)，2011，31(2)：104-108. Li Zhi，Chen Niansheng，Guo Xiaoshan，et al.Research on particle swarm algorithm and improved technology[J].Journal of Hubei Normal University(Natural Science Edition)，2011，31(2)：104-108.

[30]张立梅，唐巍.计及分布式电源的配电网前推回代潮流计算[J].电工技术学报，2010，25(8)：123-130. Zhang Limei，Tang Wei.Back/forward sweep power flow calculation method of distribution networks with DGs[J].Transactions of China Electrotechnical Society，2010，25(8)：123-130.

[31]张谦，韩维健，俞集辉，等.电动汽车充电站仿真模型及其对电网谐波影响[J].电工技术学报，2012，27(2)：159-164. Zhang Qian，Han Weijian，Yu Jihui，et al.Simulation model of electric vehicle charging station and the harmonic analysis on power grid[J].Transactions of China Electrotechnical Society，2012，27(2)：159-164.

Two-layer Smart Charge-Discharge Strategiesfor Electric Vehicles Considering Wind Generation and Users’ Satisfaction

HuangGuihongLeiXiaYangYiWangYuzheChenXiaosheng

(Key Laboratory of Power Electronic Energy-saving Technology & Equipment(Xihua University Chengdu 610039 China)

The charge-discharge dispatch problem for a large scale of electric vehicles is relevant not only to the electric grid’s secure and stable operation，but also to the providers’ economic profits and users’ feel.This paper creatively introduces the delaminating-partitioning scheduling concept and establishes a two-layer electric vehicle smart charge-discharge model.The particle swarm optimization (PSO) and the sequential selection methodare used to realize the bi-level programming simulation in MATLABto verify the modelthrough the IEEE16 node standard test system.In the upper-layer model，the maximization of the providers’ profit is ensuredthrough the gross charge-discharge power optimization to every partition at every time interval，and the effects of the charge-discharge activitieson the grid arereasonably evaded.In the lower-layer model，the target of the scheduling scheme is to satisfythe gross district charge-discharge power of the upper-layer model as far as possiblethrough optimization for the concrete charge-discharge strategiesof the electric vehicles in every district，and the users’ satisfaction is reasonably taken into consideration.At last，through the data interaction between the two layers，the coordination among the provider’s，grid’s and user’s interests are realized.

Electric vehicle，delaminating-partitioning scheduling，bi-level programming，particle swarm optimization，user’s satisfaction

2014-11-24 改稿日期2014-12-25

TM734

黄贵鸿 男，1988年生，硕士研究生，研究方向为新能源入网与电动汽车调度。(通信作者)

雷 霞 女，1973年生，教授，硕士生导师，研究方向为电力市场、调度自动化、配电自动化等。

四川省电力电子节能技术与装备重点实验室开放基金(szjj2014-015)和四川省教育厅重点项目(11za002)资助。