基于多位置NWP与主成分分析的风电功率短期预测

王丽婕 冬 雷 高 爽

(1.北京信息科技大学电气工程系 北京 100192 2.北京理工大学自动化学院 北京 100081)



基于多位置NWP与主成分分析的风电功率短期预测

王丽婕1冬 雷2高 爽2

(1.北京信息科技大学电气工程系 北京 100192 2.北京理工大学自动化学院 北京 100081)

数值天气预报(NWP)信息对风电功率短期预测模型的准确性起着重要作用。考虑风电场周围多个位置的NWP信息，提出聚类分析与主成分分析相结合的方法对风力发电功率短期预测进行研究。通过聚类分析提取历史数据中与预测日NWP最相近的样本，然后用主成分分析法对样本日信息进行处理，获得更加准确反映风电场特性的参数。通过对依兰风电场的发电功率进行预测，证实了该方法的有效性，其准确度比基于单位置NWP的预测模型提高了4.65%。

风电功率预测 数值天气预报 多位置 主成分分析 聚类分析

0 引言

随着风力发电技术的不断发展，风电单机容量和并网型风电场的规模都在不断增加，在电力需求中所占比例也越来越大。如果穿透率过高，风速的间歇性和波动性将会对电力系统的安全稳定运行以及电能质量带来不利影响[1]。如果能对风速和风电功率进行较准确的预测，可大幅降低电网旋转备用容量，从而有效降低风力发电系统成本，并为电网运行调度提供可靠的依据[2]。

风电功率预测按照预测的时间长度可分为超短期预测和短期预测。超短期预测主要使用风电场SCADA系统记录的风速、功率等历史数据来建模，可预测的尺度一般是几个小时，主要用于对风电场的运行进行控制和稳定电能质量。短期预测必须使用数值天气预报(NWP)数据，能预测提前几十个小时到几天的发电量，用于电网调度及风电功率竞价上网[3]。

我国用于风电场发电功率预测的专用数值天气预报的开发较晚，所以之前很多研究及成果都集中在风电功率的超短期预测上。文献[4，5]所采用的主成分分析法是对SCADA系统采集的风速、风向、温度、湿度等进行处理，仅能预测未来几小时的发电功率。预测时间较短，不能满足电力系统运行调度的需要。

国外对风电功率预测的研究起步较早，已经出现了很多商业软件，所以预测所需的数据比较完善。数值天气预报会直接影响风电功率预测模型的准确性[6]。文献[7]采用风电场周边多个位置的NWP信息来提高模型的准确度，但只考虑了10 m高度处的风速、风向。文献[8，9]都是使用多个NWP模型参与风电场功率预报，一个模型的分辨率低，提供初值和边值条件，另一个模型的分辨率高，提供更准确的气象信息。而我国目前还没有多个独立的天气预报系统同时进行风电场需要的气象预测。

因此，在仅有一个天气预报系统的条件下，本文提出了主成分分析法与多位置NWP相结合的短期风电功率预测方法。综合考虑风电场周围多个位置多个高度的NWP信息，首先采用聚类分析法提取出与预测日信息最相近的样本，然后用主成分分析法对样本日信息进行处理，得到对风功率影响较大的主要成分作为神经网络模型的输入。将该方法应用于我国依兰风电场的实际功率预测中，取得了令人满意的结果。

1 聚类分析

聚类分析是将研究对象按照一定度量标准分成不同类别的统计分析技术。目前较常用的一种聚类算法是K均值聚类法，其基本思想是将每一个样本划分到离均值最近的类别中，它是以距离的远近为标准进行聚类的。

K均值聚类算法一般包括以下处理步骤[10]：

(1)将所有数据分为K个初始类，选取K个样本点为初始聚类中心，记为z1(l),z2(l),…,zk(l)， 其中初始值l=1；

(2)按照最近邻规则将所有样本分配到各聚类中心所代表的K类ωj(K)中，各类所包含的样本数为Nj(l)；

(3)计算各类的均值向量，并将该向量作为新的聚类中心

(1)

式中，j=1,2,…,k；i=1,2,…,Nj(l)；

(4)若zj(l+1)≠zj(l)， 表示聚类结果并不是最佳的，则返回步骤(2)，继续迭代计算；

(5)若zj(l+1)=zj(l)， 迭代过程结束，此时的聚类结果就是最优聚类结果。

2 主成分分析的基本原理

主成分分析也称主分量分析，是揭示大样本、多变量数据或样本之间内在关系的一种方法，旨在利用降维的思想，把多变量转换为少数几个变量，降低观测空间的维数，以获取最主要的信息。

设原始变量X1，X2，…，Xp的观测n次数据矩阵为

主成分分析法的计算步骤如下[5]：

(1)将原始数据标准化，即对同一变量减去其均值再除以标准差，以消除量纲影响。

(2)

(3)

(4)

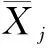
(2)求相关系数矩阵M。

(5)

且有mij=mji,mii=1。

(3)求M的特征值及特征向量。

(k=1,2,…,n;j=1,2,…,n)

(6)

(4)确定主成分的个数m。

方差贡献率和累计方差贡献率分别为

(7)

(8)

根据累计方差贡献率来选取主成分的个数。通常累计方差贡献率大于75%～95%时，对应的前m个主成分便包含p个原始变量所能提供的绝大部分信息，主成分个数就是m个，后面其他的主成分可以舍弃。

3 预测模型的建立

由于NWP的位置对于风电场的功率预测模型有一定程度的影响，建模时可选用风电场中多个位置的NWP信息综合起来考虑。NWP信息的数据间隔通常为15 min，每组信息中包含多个区域不同高度的风速、风向、温度、气压，每天的NWP数据量非常大，过多的数据加入到模型中会降低模型的泛化能力。为了获取对预测准确度影响最大的数据，首先利用聚类分析法在历史数据中查找与预测当天NWP数据最相似的样本日作为训练样本。

选取的相似样本中，每一时刻的NWP信息包含有多个位置不同高度的气象信息。通常情况下，影响风力发电功率的因素之间有一定的相关性，从而使得多位置NWP提供的信息在一定程度上有所重叠，这会增加计算的复杂性，甚至给预测带来较大误差。利用主成分分析法对这些信息进行特征提取，消除不必要的干扰项，得到对风功率影响较大的主要成分作为神经网络模型的输入，风电场的功率作为模型的输出。图1为基于多位置NWP与主成分分析的风电功率预测方法结构图。

图1 基于多位置NWP与主成分分析的功率预测结构图Fig.1 Structure diagram of prediction based on principal component analysis of NWP from multiple locations

4 实际风力发电功率预测

对我国黑龙江依兰风电场2012年1～2月的NWP数据和实测风功率数据进行分析、建模和预测。数据分辨率为15 min。选择2012年2月4日作为预测日，预测长度为一天(96步)。

欧洲中尺度气象预报中心提供了依兰风电场4个典型区域的NWP数据，4个区域的经度、纬度如图2所示。每个区域包含3个高度(34 m、67 m、112 m)，共12个位置。每个高度包括风速、气温、风向3个信息，气压信息不分位置，所以整个风电场某一时刻的NWP信息为37个：1个气压、12个风速、12个气温、12个风向。

图2 依兰风电场4个典型区域NWP数据的位置Fig.2 Four locations of NWP in Yilan wind farm

4.1 聚类分析结果

为了方便处理，将每天作为一个数据对象，由一个7维向量表示，称为日NWP向量，表示为X=[Pav，Vmin，Vmax，Tmin，Tmax，Dsin，Dcos]，其中的变量依次代表日气压平均值、日风速最小值、日风速最大值、日气温最小值、日气温最大值、日风向正弦平均值、日风向余弦平均值。

由于日NWP向量中各分量的量纲不同，需要进行归一化处理，气压、风速和气温分别除以各自的历史最大值，风向正弦和余弦值均为归一化数值，不需再作处理。

距离定义为

(9)

式中，di为预测日与历史样本i的欧氏距离；xm为预测日的日NWP向量；xi为历史数据的日NWP向量，i=1，2，…，n，其中n为样本数。

选择2012年2月4日之前的20天历史数据做聚类分析，采用K均值聚类算法，得到准则函数与分类数K的关系曲线如图3所示。取准则函数曲线拐点处的K作为最佳分类数，得到K=3。

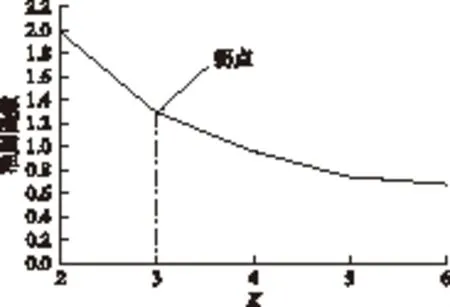
图3 准则函数与分类数K的关系Fig.3 Relationship between the criterion function and the number of categories K

在分类数K=3的情况下，20个历史样本日的所属类别情况如表1所示。其中有4天属于第3类，有1天属于第2类，其他均属于第1类。由式(1)计算出这3类的聚类中心(归一化)分别为：

第1类：[0.988 0.183 0.438 -1.130 -0.804 0.042 0.051]

第2类：[0.988 0.555 0.863 -1.151 -0.853 0.119 0.189]

第3类：[0.993 0.047 0.268 -0.856 -0.551 -0.020 -0.125]

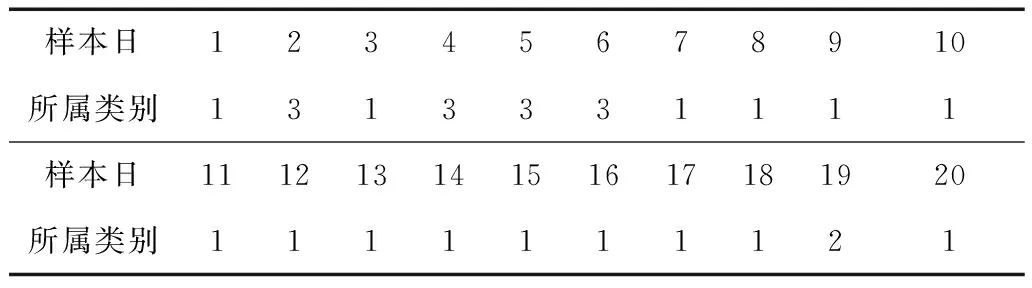
表1 样本所在聚类情况Tab.1 The clustering of the samples

预测日2月4日的归一化日NWP向量为[0.981 0.340 0.801 -0.932 -0.579 0.113 -0.052]，与3类聚类中心的欧式距离分别为0.51、0.48和0.63，距离第2类聚类中心最近，所以预测日所属分类为第2类。由表1可看出，属于第2类的样本为2012年2月2日，将其用于模型的训练中。

4.2 主成分提取

相似样本中一共有96个数据点，每个数据点有37个NWP信息，包含1个气压、12个风速、12个温度和12个风向信息。气压用P表示，由于气压只有一个，所以不做主成分提取，将其直接作为网络模型的一个输入量。v1～v12依次表示区域1高度34 m、67 m和112 m的风速、区域2高度34 m、67 m和112 m的风速、区域3高度34 m、67 m和112 m的风速、区域4高度34 m、67 m和112 m的风速；和风速的表示形式类似，t1～t12依次表示区域1、2、3、4高度34 m、67 m和112 m的气温，d1～d12依次表示区域1、2、3、4高度34 m、67 m和112 m的风向。

按照第2节介绍的主成分计算步骤分别对2月2日样本12维的风速向量、12维的风向向量和12维的气温向量进行主成分提取。计算各指标标准化后的相关系数矩阵M，M的特征值、相应的单位特征向量以及贡献率，并依据累积贡献率提取主成分。

风速主成分计算结果如表2所示，由于第一主成分的贡献率已达95%以上，所以仅选第一主成分即可。

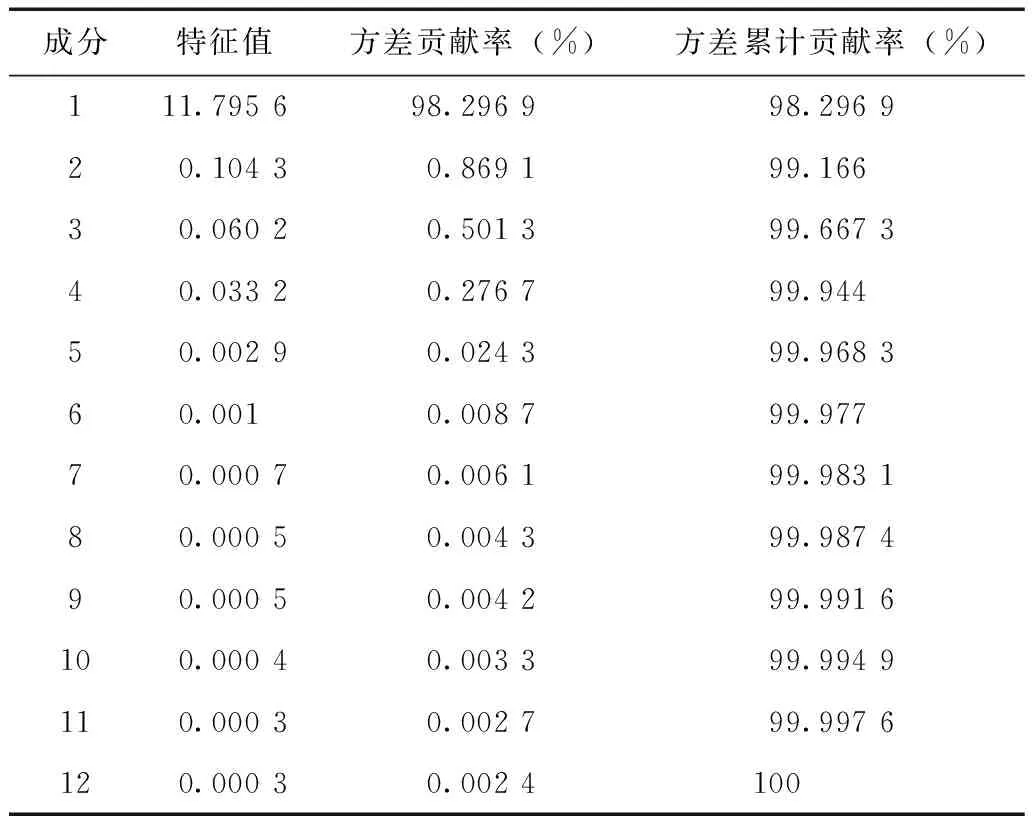
表2 风速主成分特征值及方差贡献率Tab.2 Eigenvalues and contribution rate of wind speed principal component

气温主成分计算结果如表3所示，由于第一主成分的贡献率已达99%以上，所以仅选第一主成分即可。

风向主成分计算结果如表4所示，由于第一主成分的贡献率已达95%以上，所以仅选第一主成分即可。

经过主成分提取，得到了更加准确反映风电场特性的参数。其中，12维的风速向量降低到1维，第一主成分分量记为VPCA1；12维的气温向量降低到1维，第一主成分分量记为TPCA1；12维的风向向量降低到1维，第一主成分分量记为DPCA1。

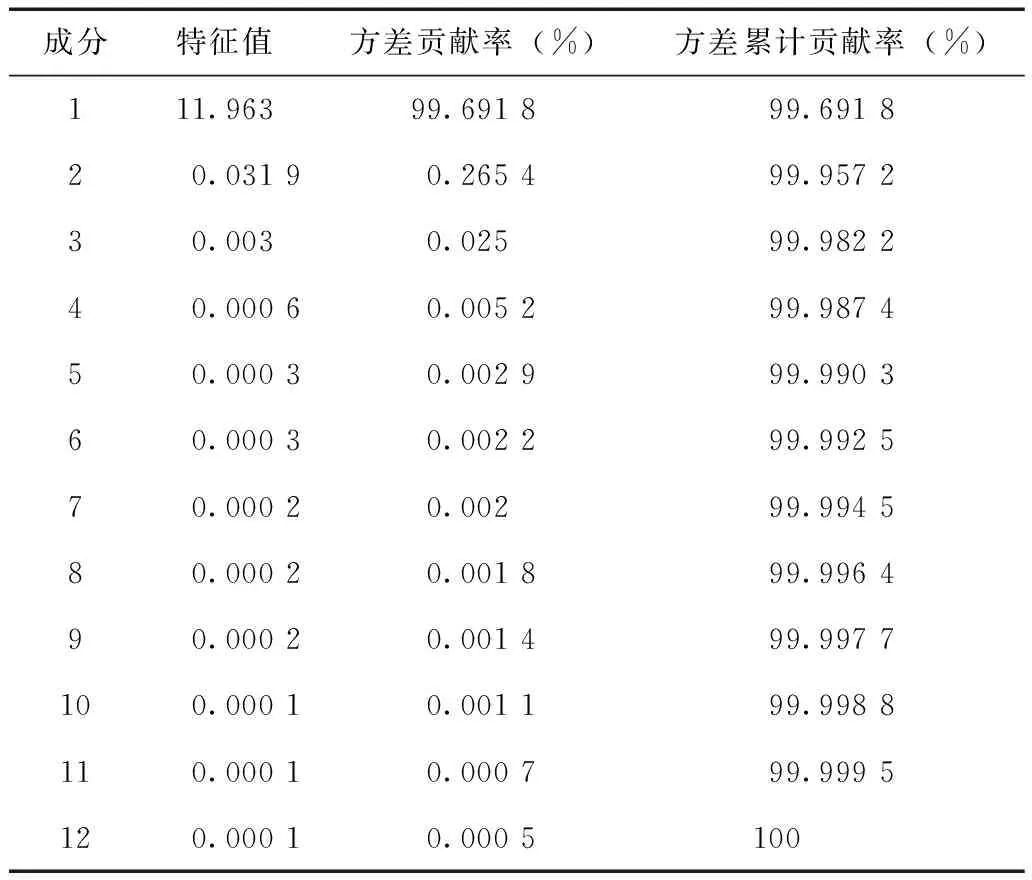
表3 气温主成分特征值及方差贡献率Tab.3 Eigenvalues and contribution rate of temperature principal component

表4 风向主成分特征值及方差贡献率Tab.4 Eigenvalues and contribution rate of wind direction principal component

4.3 模型建立与仿真结果

选取VPCA1、DPCA1、TPCA1这3个主成分分量和气压作为预测模型的输入，记为PCA-4维，预测模型采用GRNN神经网络，GRNN窗口宽度参数s=0.5，对应时刻的风功率作为模型的输出，用2月2日数据进行训练，得到预测模型。随后，对2月4日的发电功率进行预测。

图4为各种模型的预测曲线，其中持续模型是国外普遍使用的一种参考模型[11]。从图中可看出，利用多位置NWP建模包含的信息量多，预测值最接近于实际值。而基于单位置NWP的模型只考虑了风电场中一个位置的气象信息，天气预报的误差导致多个点的风电功率预测值低于真实值。

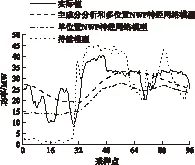
图4 各种模型预测结果对比Fig.4 Comparison of different prediction models

表5列出了各种模型的平均绝对误差(NMAE)、均方根误差(NRMSE)和最大预测误差(δmax)[12]。由表5可知，采用多位置NWP的神经网络模型的各种预测误差最小，平均绝对误差和均方根误差分别为风电场总装机容量的12.35%和15.66%，整体预测效果较好，可满足工程应用的需要。其平均绝对误差比采用单位置NWP建模提高了4.65%，比持续模型提高了近10%。多个位置的NWP包含的信息量多，充分考虑了风电场周围的气象状况，可显著提高模型的预测准确度，使预测值更接近于实际值。

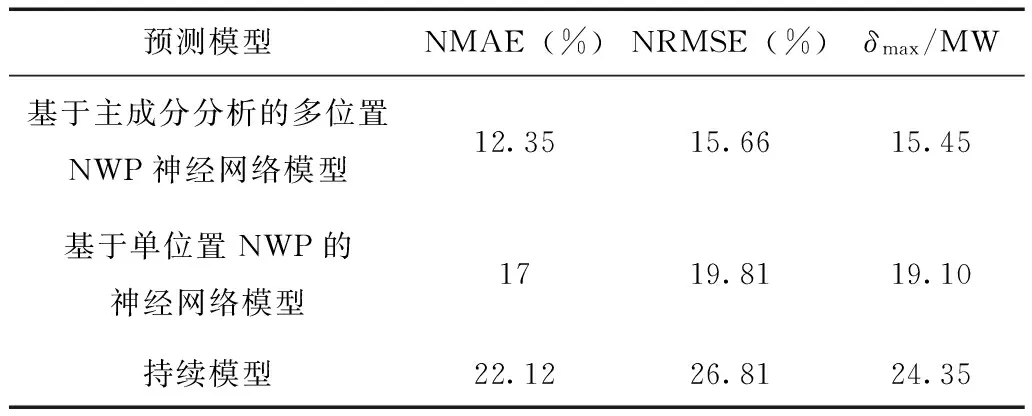
表5 预测模型的误差对比Tab.5 Errors of different prediction models

5 结论

由于数值天气预报信息对风电功率预测的准确性有较大影响，本文将聚类分析、主成分分析、多位置NWP三者结合起来，进行风力发电功率的预测。多位置NWP包含了风电场周围不同地点不同高度的气象信息，聚类分析能提取出与预测日NWP最接近的历史数据来作为训练样本，主成分分析能获得更加准确反映风电场特性的参数。该方法有效降低了训练数据量，减少了输入样本的维数，降低了网络训练的难度，提高了模型的预测准确度。与只使用一个位置NWP建模相比，风电功率预测的平均绝对误差由17%降低到12.35%。

[1] 张丽英，叶廷路，辛耀中，等.大规模风电接入电网的相关问题及措施[J].中国电机工程学报，2010，30(25)：1-9. Zhang Liying，Ye Tinglu，Xin Yaozhong，et al.Problems and measures of power grid accommodating large scale wind power[J].Proceedings of the CSEE，2010，30(25)：1-9.

[2] 王贺，胡志坚，张翌晖，等.基于聚类经验模态分解和最小二乘支持相量机的短期风速组合预测[J].电工技术学报，2014，29(4)：237-245. Wang He，Hu Zhijian，Zhang Yihui，et al.A hybrid model for short-term wind speed forecasting based on ensemble empirical mode decomposition and least squares support vector machines[J].Transactions of China Electrotechnical Society，2014，29(4)：237-245.

[3] Soman S S，Zareipour H，Malik O，et al.A review of wind power and wind speed forecasting methods with different time horizons[C].North American Power Symposium (NAPS)，Arlington，TX，2010：1-8.

[4] 何东，刘瑞叶.基于主成分分析的神经网络动态集成风功率超短期预测[J].电力系统保护与控制，2013，41(4)：50-54. He Dong，Liu Ruiye.Ultra-short-term wind power prediction using ANN ensemble based on the principal components analysis[J].Power System Protection and Control，2013，41(4)：50-54.

[5] 周松林，茆美琴，苏建徽.基于主成分分析与人工神经网络的风电功率预测[J].电网技术，2011，35(9)：128-132. Zhou Songlin，Mao Meiqin，Su Jianhui.Prediction of wind power based on principal component analysis and artificial neural network[J].Power System Technology，2011，35(9)：128-132.

[6] Ernst B，Oakleaf B，Ahlstrom M L，et al.Predicting the wind[J].IEEE Power & Energy Magazine，2007，10(11)：79-89.

[7] Khalid M，Savkin A V.A method for short-term wind power prediction with multiple observation points[J].IEEE Transactions on Power Systems，2012，27(2)：579-586.

[8] Stathopoulos Christos，Kaperoni Akrivi，Galanis George，et al.Wind power prediction based on numerical and statistical models[J].Journal of Wind Engineering and Industrial Aerodynamics，2013，112(1)：25-38.

[9] Lazic Lazar，Pejanovic Goran，Zivkovic Momcilo.Wind forecasts for wind power generation using the Eta model[J].Renewable Energy，2010，35(6)：1236-1243.

[10]Wei Wei，Zhang Yajie，Wu Guilian，et al.Ultra-short-term/short-term wind power continuous prediction based on fuzzy clustering analysis[C].IEEE Innovative Smart Grid Technologies-Asia，2012：1-6.

[11]Sideratos G，Hatziargyriou N.Using radial basis neural networks to estimate wind power production[C].IEEE Power Engineering Society General Meeting，2007：1-7.

[12]Q/GDW 588-2011.风电功率预测功能规范[S].

Wind Power Short-term Prediction Based on Principal Component Analysis of NWP of Multiple Locations

WangLijie1DongLei2GaoShuang2

(1.Beijing Information Science and Technology University Beijing 100192 China 2.Beijing Institute of Technology Beijing 100081 China)

Numerical weather prediction (NWP) plays an important role in the accuracy of the short-term wind power prediction models.Considering NWP information of multiple locations around a wind farm，this paper introduces a method based on the cluster analysis and the principal component analysis to study the short-term prediction of the wind power generating capacity.The sample in the historical data closest to the NWP of the forecast day is extracted by the clustering analysis.Then the principal component analysis of the sample information is proceeded to obtain the parameters which reflects the characteristics of the wind farm.Simulation is performed consideringthe wind power generation of Yilan wind farm.The results show that the method is effective and its precision improves 4.65% than the prediction model based on NWP of single location.

Wind power prediction，numerical weather prediction，multiple locations，principal component analysis，cluster analysis

2014-11-20 改稿日期2015-01-05

TM614

王丽婕 女，1983年生，博士，研究方向为风力发电功率预测及风电并网后的运行控制。(通信作者)

冬 雷 男，1967年生，副教授，博士，研究方向为电力电子与电力传动以及新能源发电等。

北京市教委科技计划面上项目(KM201511232007)资助。