一种异步电动机静止状态下参数辨识的改进方法

刘 鹏 吴文进 苏建徽

(合肥工业大学教育部光伏系统工程研究中心 合肥 230009)



一种异步电动机静止状态下参数辨识的改进方法

刘 鹏 吴文进 苏建徽

(合肥工业大学教育部光伏系统工程研究中心 合肥 230009)

基于异步电动机的非对称T型模型，提出一种电动机静止状态下参数辨识的改进算法。分析并指出逆变器死区只对输出电压有功分量产生影响，并通过对死区自适应补偿方法辨识出电动机参数，提高了辨识的准确度。考虑到趋肤效应的影响，给出通过两次注入相同转差频率、不同幅值的单相交流电流，并通过对误差电压进行对消的自适应算法辨识出转子电阻；基于等效空载的方法，注入极低频率的单相交流电流使电动机在静止状态与空载旋转状态等效，避免了转子电阻的影响，从而更精确的辨识出互感。将所测量参数与利用传统方法测量的参数进行对比，并将参数用于无速度传感器矢量控制，验证了该算法具有较高的精确性、实用性和鲁棒性。

异步电动机 参数辨识 死区影响 自适应算法 等效空载方法

0 引言

异步电动机因具有价格低、可靠性高等优点而被广泛应用。众所周知，矢量控制等高性能控制算法的控制性能依赖电动机参数的准确度[1，2]。为辨识异步电动机参数，传统方法是基于电机的空载和堵转实验[3]，但在实际应用中，尤其当系统安装完毕负载难于拆卸时，这种方法就不适用了。

为了在静止状态下辨识出异步电动机参数，国内外学者做了很多工作。文献[4-7]基于异步电动机T型模型提出了频率响应法，但未考虑死区对辨识结果的影响；文献[8]对死区的影响提出了一种补偿方法，但这种方法对漏感变化比较敏感，有可能出现过补偿导致辨识结果错误；文献[9]通过施加特定的激励电流，通过调节转子时间常数将定子电压变化率调节为零，进而估算出转子时间常数，避免了死区的影响，但对于转子时间常数大的电机辨识准确度较低，且并未给出异步电动机全参数的辨识方法；文献[10]基于异步电动机全阶模型采用模型参考的方法辨识电动机参数，但其自适应观测器过于复杂，计算量大，不利于工程应用；文献[11]采用最小二乘法辨识电动机参数；文献[12-14]提出采用智能算法辨识电动机参数。但这些方法计算非常复杂，均不利于实际工程应用。

本文提出一种异步电动机静止状态下参数辨识的改进方法。通过注入不同频率单相电流，在静止条件下对异步电动机各参数进行辨识，同时对死区造成的误差采取自适应补偿的方式，提高了参数辨识的准确性和鲁棒性。最后通过实验验证了所提方法的正确性和实用性。

1 异步电动机参数辨识模型

静止状态下异步电动机的单相反T型等效电路如图1所示。图中Rs、Lσ、Lm、Rr分别为定子电阻、漏感、互感和转子电阻。

图1 异步电动机非对称T型等效电路Fig.1 The asymmetric T type equivalent circuit of induction motor at standstill

本文所采用的参数辨识方法是基于图1所示T型等效电路进行的。

2 参数辨识方案

参数辨识方案所采用的主电路包括电压源型变流器(VSI)和异步电动机，如图2所示。

图2 电压型逆变器与异步电动机Fig.2 Voltage source inverter and induction motor

为了向相应的电动机绕组注入需要的电流，可以使B、C相电压等于零，通过控制A相电压来达到控制电流的目的。为此可以使VT3、VT4和VT5、VT6导通占空比为50%，而通过控制VT1、VT2的占空比来控制A相电压，其等效电路如图3所示。

图3 异步电动机定子等效电路Fig.3 Equivalent circuit of induction motor stator

B、C相绕组并联后与A相绕组串联。由图3可知，辨识出的每个电动机参数均为实际电动机参数的 1.5倍。为避免开环控制时变频器可能出现过流，同时为使电流达到指定的电流值，系统控制采用电流闭环，其控制框图如图4所示。

图4 电流注入控制框图Fig.4 Control structure of current injection

3 逆变器死区影响分析

在电压源型变流器中，由于开关器件并非理想器件，为防止上、下桥臂直通，必须插入一段死区时间。由于死区时间的存在，电动机端口实际输出电压并不等于指令电压。由于在电动机静止参数辨识中，施加于电动机定子上的电压一般较小，死区的存在将导致辨识结果与实际偏差较大[15，16]。

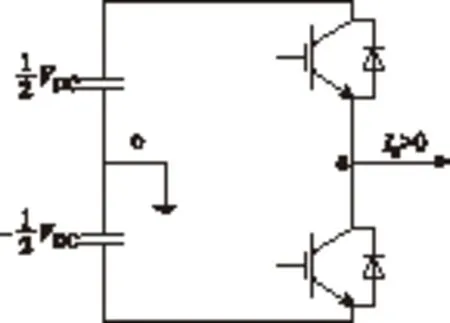
图5 VSI的通用桥臂Fig.5 General leg of VSI

图6 误差电压产生的机理Fig.6 The mechanism of the disturbance voltage

图5所示为VSI的一个桥臂，定义电流流出VSI的方向为正方向，流进VSI的方向为负方向。图6为一个开关周期Ts内，开关信号与桥臂输出电压关系。在理想情况下上、下桥臂驱动信号互补如图6a所示，其所对应的桥臂电压如图6b所示。在插入死区后上、下桥臂的驱动信号上升沿均向后延时Td，如图6c所示。当电流Ia>0时，在死区时间Td内，电流的续流回路经过下桥臂的二极管，此时虽然下桥臂未开通信号，但因二极管导通，a点电位为-UDC/2，与下桥臂开关管开通的状态相同，故此时桥臂输出电压如图6d所示。由此可算出当Ia>0的情况下，在一个开关周期内，由于死区导致的误差电压Uda如图6d阴影部分所示，根据面积等效原理有Uda=-UDCTd/Ts。同理当Ia<0的情况下，一个PWM周期内死区造成的误差电压如图6e所示，误差电压Uda=UDCTd/Ts。同理可推广至B、C两相。故可得出由死区造成的误差电压的一般表达式为

Udn=-sign(in)UDCTdn/Ts

(1)

式中，n=a，b，c；UDC为直流电压；Udn为死区误差电压；in为VSI相电流；Td为死区时间；Ts为PWM周期。

(2)

根据式(1)、式(2)可知，由死区造成的误差电压与电流方向相反。将逆变器给定电压Unref改写为矢量形式为

Unref=Re(Unref)+jIm(Unref)

(3)

取电流in方向为参考方向，可得电流in、给定电压Unref和实际电压Unact之间的关系如图7所示。

图7 定子电流、给定电压与实际电压关系示意图Fig.7 Relationship of stator current，reference output voltage and actual output voltage

由图7可知，在考虑死区电压影响后，桥臂实际输出电压为

Unact=Re(Unref)-Udn+jIm(Unref)

(4)

由图7和式(4)可看出输出电压矢量的虚部并不受死区的影响。且由式(4)可知由每个桥臂上死区造成的误差电压幅值不变且只与电流方向有关。根据以上结论可知，死区造成的误差只对输出电压的有功分量造成影响，对无功分量无影响。在对电动机参数进行辨识时，应尽量选择用电压的虚部进行辨识，如果选用实部则应对死区造成的误差进行补偿[17]。

4 电动机参数辨识

根据以上辨识方案并考虑到逆变器死区的影响，下面将对电动机各参数进行辨识。根据不同参数之间的依赖关系，将依次对定子电阻、漏感、转子电阻和互感等参数进行精确测量。

4.1 定子电阻的测量

在对电动机定子电阻进行辨识时，对定子两次注入直流电流，求得其电流与电压的增量进而计算出定子电阻，这样避免了死区对输出电压造成的影响。

对电动机定子注入直流电流时，电感的阻抗为零，转子电阻被短路，其等效电路如图8所示。图中X端与B、C端相连。

图8 定子电阻辨识等效电路Fig.8 Equivalent circuit of stator resistor estimation

向绕组中分别注入电流Ia1、Ia2，由于死区的影响，可得式(5)、式(6)。

UAX1+Udn=Ia1Rs

(5)

UAX2+Udn=Ia2Rs

(6)

为消除死区的影响，将式(6)与式(5)相减并计算得到定子电阻Rs。

(7)

4.2 漏感的测量

在对漏感进行辨识时，向电动机绕组中注入较高频率的电流，使其满足ωLm≫Rr，这样使互感回路处于开路状态，再将注入电压的无功分量提取出来，既可避免互感的影响，又可避免定、转子电阻对辨识结果造成的影响。其等效电路如图9所示。

图9 漏感辨识的等效电路Fig.9 Equivalent circuit of leakage inductor estimation

由于电压的虚部不受死区影响，以电流Ia作为参考，根据电路原理可得

(8)

于是可得漏感Lσ

(9)

4.3 转子电阻的测量

转子电阻的辨识需要对注入电流的频率进行选择。传统方法是采用高频注入的方法，互感支路处于开路状态，电流完全流入转子电阻支路，较方便地测量出转子电阻。但这种方法未考虑到电动机的趋肤效应对转子电阻的影响，为此需降低注入电流的频率。在电动机运行过程中，转子电流的频率为转差频率，本文选取注入电流的频率为电动机在实际运行时额定转差率附近的频率，这样可以使辨识结果更加接近实际运行时的真实值。但在这个频率下，互感的影响是不能忽略，因此其等效电路如图10所示。考虑到死区效应的影响，可选择两次注入相同频率、不同幅值的电流[18]。

图10 转子电阻辨识等效电路Fig.10 Equivalent circuit of rotor resistor estimation

于是有

UAX1+Udn=Ia1(RAX+jωeLAX)

(10)

UAX2+Udn=Ia2(RAX+jωeLAX)

(11)

式(10)与式(11)相减可得

(UAX1-UAX2)=(Ia1-Ia2)(RAX+jωeLAX)

(12)

式中，RAX、jXAX分别为AX输入口的等效电阻和等效电抗；Udn为死区造成的误差电压。根据电路原理，电机的励磁电压如式(13)、式(14)。

Ue1=UAX1+Udn-Ia1(Rs+jωeLσ)

(13)

Ue2=UAX2+Udn-Ia2(Rs+jωeLσ)

(14)

式(13)与式(14)相减可得

Ue1-Ue2=UAX1-UAX2-(Ia1-Ia2)(Rs+jωeLσ)

(15)

又由

(16)

RrIa2cosα=Ue2

(17)

其中

(18)

将式(15)代入式(16)中可得

(19)

4.4 互感的测量

传统测量互感的方法是将电动机空载运行，此时转子电阻处于开路状态，回路中只有定子电阻、漏感、互感，可以很容易地辨识出互感。文献[8]通过两次注入不同频率的交流电流来求取电动机互感，但这种方法未考虑到在不同频率的条件下，由于趋肤效应的影响，转子电阻不同，因而会带来测量的误差。

本文提出一种基于等效空载测量互感的改进方法，即在电动机静止的条件下，通过模拟空载时电动机状态的方法来测量电动机互感。异步电动机转子等效电阻为(1-s)Rr/s， 其中s为转差率。当电动机空载时转差率很小，转子等效电阻很大，在其等效电路中，转子电阻可认为处于开路状态。如果在电动机定子中注入频率极低的电流，使其满足ωeLm≪Rr， 此时互感压降极小，与互感并联的转子电阻支路近似开路，大部分电流流入互感支路，使电动机在静止状态与空载旋转状态近似等效，避免了转子电阻的影响，从而能更精确的辨识出互感。其等效电路如图11所示。

图11 互感辨识等效电路Fig.11 Equivalent circuit of mutual inductor estimation

由前文分析可知，死区对输出电压的无功分量并无影响，故可利用电压虚部直接求出互感，如式(20)、式(21)。

(20)

Lm=Ls-Lσ

(21)

采用等效空载的方法，注入频率极低的电流，并将输入电压的无功部分提取出进行计算，可同时避免转子电阻和定子电阻对辨识结果造成的影响，使得辨识结果更加接近真实值，提高了辨识准确度。

5 实验验证

为验证本文方法的有效性，在实验室搭建了逆变器实验平台，控制芯片为TMS320F28335，采用10K开关频率，死区时间为2.5μs。利用该控制平台分别对15kW和11kW两台异步电动机参数进行辨识。

图12为对15kW异步电动机进行参数辨识的实验波形。在测量定子电阻过程中，首先向电动机定子注入20A电流，测量数据完毕后等待5s，再次注入10A电流并测量数据，将两次测得数据代入式(7)即可得电动机定子电阻值。图12b为测量异步电动机漏感时的电流波形，测量时对电动机定子注入单相较高频率的交流电流，这里选择注入25Hz交流电流，测出电动机定子的无功电压和电流。图12c为测量异步电动机转子电阻时的电流波形，考虑到趋肤效应的影响，这里选择向电动机定子注入频率为1Hz的交流电流。图12d为测量互感的电流波形，为使转子支路处于等效开路状态，选择注入频率为0.03Hz交流电流。

图12 参数辨识实验波形Fig.12 Experimental waveform of induction motor parameters estimation

表1、表2为采用本文辨识方法分别对15kW和11kW两台异步电动机参数进行多次辨识的测量结果，可看出辨识结果比较稳定。表3为利用传统空载、堵转实验方法对同样的两台异步电动机进行参数辨识的结果。表4为本文辨识方法与传统辨识方法的相对误差，计算结果表明了本文方法的精确性。

表1 15 kW异步电动机静止状态下参数辨识结果Tab.1 The parameter identification results of 15 kW motor at standstill

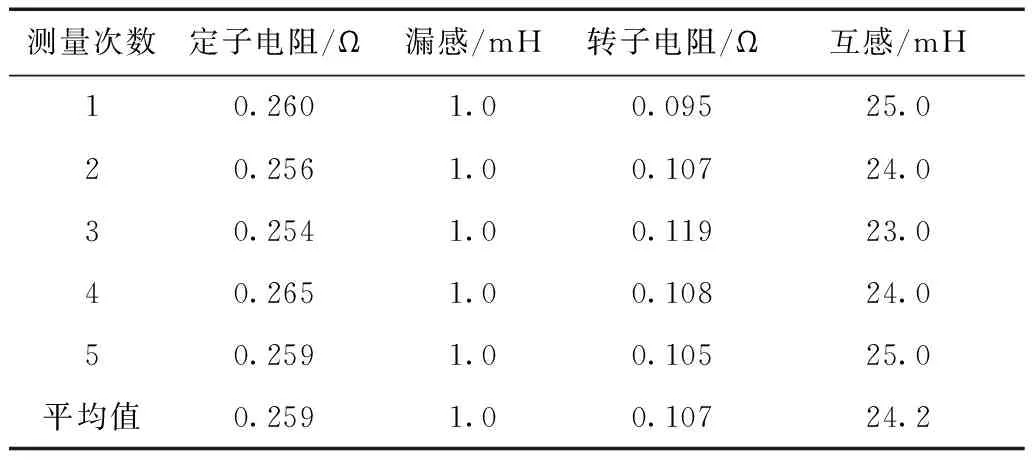
表2 11 kW异步电动机静止状态下参数辨识结果Tab.2 The parameter identification results of 11 kW motor at standstill

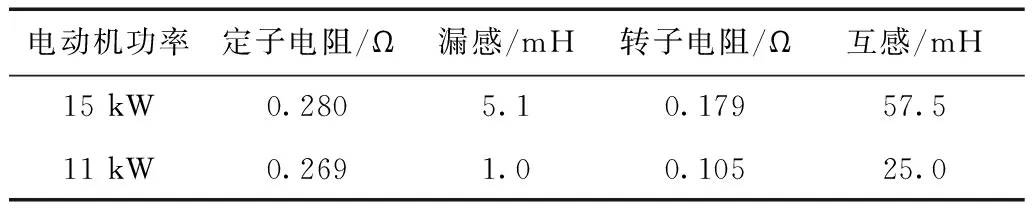
表3 基于传统空载、堵转实验方法的参数辨识结果Tab.3 The parameter identification results based on the traditional no-load and stalling experimental methods

表4 本文辨识方法与传统辨识方法的相对误差Tab.4 The parameter identification relative errors based on the two methods

用本文方法辨识的异步电动机参数用于无速度传感器矢量控制，其估算转速与实际转速对比如图13所示，转速估算精确度高，提高了系统控制的精确性、实用性和鲁棒性。

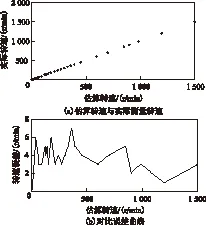
图13 无速度传感器矢量控制转速测量结果Fig.13 The result of a measurement for motor rotation speed in the sensor-less vector control system

6 结论

本文通过分析死区对电压源型逆变器输出电压的影响，给出了一种对死区误差进行自行抵消的自适应补偿方法，在此基础上提出了对异步电动机静止状态下各参数进行辨识的改进方法。搭建了实验平台，并利用该方法分别对15 kW和11 kW两台异步电动机参数进行辨识，实验结果表明了该辨识方法的有效性。

[1] Holtz J.Sensorless position control of induction motors an emerging technology[J].IEEE Transactions on Industrial Electronics，1998，45(3)：840-852.

[2] Toliyat H A，Levi E，Raina M.A review of RFO induction motor parameter estimation techniques[J].IEEE Transaction on Energy Conversion，2003，18(2)：271-283.

[3] 贺艳晖，王跃，王兆安.异步电机参数离线辨识改进算法[J].电工技术学报，2011，26(6)：73-80. He Yanhui，Wang Yue，Wang Zhao’an.An improved off-line parameter identification algorithm for induction motors[J].Transactions of China Electrotechnical Society，2011，26(6)：73-80.

[4] Jul K S，Seung I M，Seung K S.Induction machine parameter identification using PWM Inverter at Standstill[J].IEEE Transactions on Energy Conversion，1997，12(2)：127-132.

[5] Ganji A，Guillaume P，Pintelon R，et al.Induction motor dynamic and static inductance identification using a broadband excitation technique[J].IEEE Transactions on Energy Conversion，1998，13(1)：15-20.

[6] Klaes N R.Parameters identification of an induction machine with regard to dependencies on saturation[J].IEEE Transactions on Industry Applications，1993，29(6)：1135-1140.

[7] Young S K，Jeong H L，Sang H M，et al.Standstill parameter identification of vector-controlled induction motors using the frequency characteristics of rotor bars[J].IEEE Transactions on Industry Applications，2009，45(5)：1610-1618.

[8] 陈伟，于泳，徐殿国，等.基于自适应补偿的异步电机静止参数辨识方法[J].中国电机工程学报，2012，32(6)：156-162. Chen Wei，Yu Yong，Xu Dianguo，et al.Parameters estimation of induction motors at standstill with adaptive non-linearity compensation[J].Proceedings of the CSEE，2012，32(6)：156-162.

[9] 盛爽，陆海峰，程小猛，等.静止状态异步电机转子时间常数辨识[J].清华大学学报(自然科学版)，2012，52(12)：1771-1776. Sheng Shuang，Lu Haifeng，Cheng Xiaomeng，et al.Rotor time constant identification for a stationary induction motor[J].Journal of Tsinghua University(Sci & Tech)，2012，52(12)：1771-1776.

[10]Peresada S，kovbasa S，Prystupa D.Adaptive observers for self commissioning of induction motor drives：Theory and experiment[C].IEEE International Conference on Intelligent Energy and Power Systems，2014，240-245.

[11]张虎，李正熙，童朝南.基于递推最小二乘算法的感应电动机参数离线辨识[J].中国电机工程学报，2011，31(18)：79-86. Zhang Hu，Li Zhengxi，Tong Chaonan.Off-line parameter identification of induction motor based on recursive least squares algorithm[J].Proceedings of the CSEE，2011，31(18)：79-86.

[12]Bachir A，Azeddine B，Nasreddine N S，Application of genetic algorithm with a novel adaptive scheme for the identification of induction machine parameters[J].IEEE Transactions on Energy Conversion，2005，20(2)：284-291.

[13]Bechouche A，Sediki H，Abdeslam D O，et al.A novel method for identifying parameters of induction motors at standstill using adaline[J].IEEE Transactions on Energy Conversion，2012，27(1)：105-115.

[14]Zai L，De C L，Lipo T A.An extended Kalman filter approach to rotor time constant measurement in PWM induction motor drives[J].IEEE Transactions on Industrial Electronics，1992，28(1)：96-104.

[15]何正义，季学武，瞿文龙.一种新颖的基于死区时间在线调整的SVPWM补偿算法[J].电工技术学报，2009，24(6)：42-47. He Zhengyi，Ji Xuewu，Qu Wenlong.A novel SVPWM compensation strategy based on regulating dead time on line[J].Transactions of China Electrotechnical Society，2009，24(6)：42-47.

[16]Zhao H，Jonathan Q M，Kawamura A.An accurate approach of nonlinearity compensation for VSI inverter output voltage[J].IEEE Transactions on Power electronics，2004，19(4)：1029-1035.

[17]Consoli A，Fortuna L，Gallo A.Induction motor identification by a microcomputer based structure[J].IEEE Transactions on Industrial Electronics，1987，34(4)：422-428.

[18]李东钰(译)，杨耕(校).感应电机离线参数辨识方法[J].电力电子，2009，7(3)：9-16. Li Dongyu，Yang Geng.Motor constants measurement for induction motors without rotating[J].Power Electronic，2009，7(3)：9-16.

An Improved Parameters Estimation Algorithm for Induction Motor in the Standstill State

LiuPengWuWenjinSuJianhui

(Research Center of Photovoltaic System Engineering of Ministry of Education Hefei University of Technology Hefei 230009 China)

In order to obtain the accurate induction motor (IM) parameters in the standstill state，an improved algorithm for parameter identification based on the asymmetric T type circuit is proposed.It is proved that only the active component of the output voltage is affected by the inverter dead time.Based on it，the accuracy of IM parameters estimation is improved through the adaptive compensation for the inverter dead time.The rotor resistor is identified through injecting two single phase alternating currents with identical slip frequency，and different amplitudes，proposing the adaptive algorithm of cancellation error voltage，and considering the skin effect.Based on the approach of equivalent motor idling，mutual inductance is identified more accurately through injecting the very low frequency single phase alternating current and eliminating the influence of the rotor resistance.All the IM parameters estimated in the standstill state is compared with the IM parameters measured by the traditional method and used in the sensor-less vector control system.The experimental results show that the proposed parameter identification algorithm has high accuracy，practicality，and robustness.

Induction motor，parameter identification，impact of dead time，adaptive algorithm，the equivalent idling method

国家自然科学基金(51207040；51307042)。

2014-11-06 改稿日期2014-12-21

TM315

刘 鹏 男，1984年生，博士研究生，研究方向为电机传动及新能源利用技术。(通信作者)

吴文进 男，1975年生，博士研究生，副教授，研究方向为电机传动及新能源利用技术。