三维激光扫描技术在复杂地质隧道岩体信息获取中的优化
2015-03-28白明洲张云龙
师 海,白明洲,李 丽,田 岗,张云龙
(1.北京交通大学 土木建筑工程学院,北京100044;2.中国地质环境监测院,北京100081)
岩溶隧道施工条件和地质环境复杂,一直是困扰隧道设计与施工人员的技术难题,传统的获得岩石信息和监测的方式工作量大、效率较低,且存在安全隐患[1]。三维激光扫描技术具备高采样率,可较快速、精准地反映出待测目标的真实状态,因此将三维激光扫描应用到隧道等地下工程的岩体的结构面信息采集工作中[2-4],以便可以确切的反映隧道内地学目标点的切实、复杂状态。但利用三维激光扫描仪快速获取的隧道掌子面扫描区域的海量岩体三维点云数据中,由于在扫描过程中受到岩溶隧道内机械设备的遮挡、长距离、大入射角扫描等影响,引起扫描点异常的可能性较大,不可避免的对获取的岩体信息—结构面产状的精度产生影响[5-7]。因此,有必要对获取的海量点云数据进行滤波插值,只有将这些影响精度的点云数据进行滤波插值后,才能在岩溶隧道岩体信息获取和分析中有效利用,为最终生成DEM服务[5]。目前,点云数据插值方法主要包括平面拟合法、最小二乘法、基于分类的算法、基于地形坡度的方法、基于形态学开运算方法等[6-8]。但是,岩溶隧道围岩的变形主要是由岩块的转动、滑移,岩石弹塑性变形等引起,形态比较复杂,而且传统的单一插值方法很难同时考虑到各种影响因素的关系,为了发挥各种方法的优势,提高岩体结构面信息--产状获取的精度,提出将Kriging算子和最小二乘法插值理论结合,形成组合插值方法,借助三维激光扫描技术更加准确的获取正在施工中的岩溶隧道岩体信息—结构面产状。
1 点云插值理论模型的建立
利用三维激光扫描技术获取大量的岩溶隧道岩体的点云数据之后,一个重要的步骤是插值,使用单一的插值模型具有不稳定性,因此应用基于Kriging算法和最小二乘法的组合方法,它是在原始点云数据的基础上,应用最小二乘法的原理建立遗传算法目标函数,改进Kriging算法的变异函数理论模型,使得获取信息的精度提高,也即为组合插值理论,并通过实例验证优化Kriging插值方法在处理点云、获取岩溶隧道岩体信息的实际应用中的优势。
1.1 Kriging插值理论
Kriging算法既考虑已知点云位置与待估点云位置相关关系,还考虑各个扫描点的空间相关性,是一种拥有无偏性、方差小和线性等特征的空间插值方法,应用它可计算出各个估值的误差,而且可得到估值的可信度。在应用三维激光扫描技术获得岩溶隧道掌子面点云数据基础上,构建出一个只与点云之间的空间距离间隔关联的半方差函数,则可求出各拟合点的权系数,据此进行点云之间的高程内插,并通过后处理获取岩体的信息[9-10]。
假设Z*(xi,yi)是扫描获取的点云承载区域化的变量,在扫描区域内的n个位置上取样,记为Z*(x1,y1),Z*(x2,y2),…,Z*(xn,yn),则 在 点云区域内某点(xp,yp)的估值为
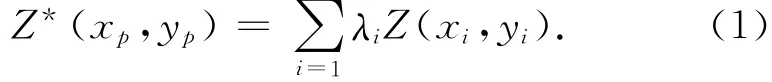


式中:μ为拉格朗日乘子;γ(xi,yi)为变异函数,求出λi后便可以计算出预估点云的高程值。
根据以上原理就可将通过三维激光扫描技术获得的点云数据进行插值。Kriging算子的优点是:采样点的个数可多可少。因此,用此方法插值的结果往往更接近实际情况。但针对正在施工的岩溶隧道,点云数据较多,所以基于Kriging算子的插值方法计算较复杂,且速度慢。
1.2 最小二乘法拟合理论
最小二乘法是一种数学优化技术。应用其拟合三维激光扫描技术获得岩溶隧道掌子面点云曲线关键在于利用最小化误差的平方和寻求数据的最有利函数匹配。
设获取的已知点云数据(xi,yi)(i=1,2,…,m)及各点的权系数ai,求出点云数据x与拟合的曲线y 之间的函数关系y=s(x;a0,a1,…,an),其中i=0,1,…,m(m<n),由于最小二乘法只要求误差的最小值。则假设逼近函数为
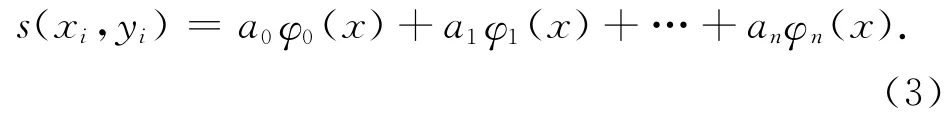
式(3)的最小值


将式(5)根据内积的定义,改成关于a0,a1,…,an的线性方程组,其矩阵形式为

由于φ0x φ1x φnx 是线性无关的,则可求出其唯一解ak=a*k,k=0,1,…,n。
利用最小二乘法进行差值只需求解目标函数的极值,因而计算简单、速度快。但是其存在一个缺点,即所有插值点云数据对结果的贡献都是均等的,它没有考虑到其中对最后结果有影响的异常点,因而往往使得最后得到的结果与实际情况存在差异[12]。
1.3 基于Kriging算法和最小二乘法的组合理论
针对上述情况,根据岩溶隧道岩性较差、施工环境相对恶劣等因素,可知在三维激光扫描技术中获取岩石产状,受到许多因素综合作用的影响,如果只是采用一种插值模型,则不能够全面、精确的提取出产状信息。在参考和总结以前的研究后,针对上述情况及Kriging算子和最小二乘拟合法在滤波插值中本身的缺点,提出一种利用函数参数估计插值的方法,即将Kriging算子插值法与最小二乘法曲面拟合相结合。
基于Kriging算法和最小二乘法组合方法是针对Kriging插值函数在距离不同的区域内,插值的点云数目的不同,确定和分析其可信度。即点云数目越多,插值函数越可信,所以在插值拟合时考虑在式(4)的基础上增加权重系数。其主要根据是最小二乘法原理对原始的点云数据实施变换,加入合适的权重系数ωi,据此分析,权重系数:

其中n(h)为距离相隔h的点云的数目。则组合插值模型的目标函数为
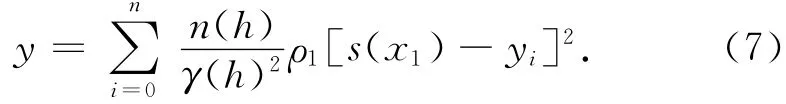
2 工程实例
新建沪昆铁路客运专线湖南段雪峰山1号隧道为特长隧道,涌水量大,穿越多条断层及石水坑、吉祥村大型背斜构造,地质条件极为复杂,工期风险很大。其构造属于剥蚀、溶蚀中低山地貌。隧道范围内地表为第四系全新统冲洪积岩(Q4),上更新统残坡积层(Q3),下伏基岩为震旦系上统金家洞组(Z2j),下统洪江组(Z1hj)。针对本区域内岩溶隧道的情况,使用徕卡HDS-4400三维激光扫描仪见图1(a)。
2.1 岩溶隧道掌子面点云数据的获取
由于三维激光扫描仪架设基点的确定需要进行大地坐标的转换,但是受到此岩溶隧道复杂的施工场地及起伏地形的限制,为了方便快速识别坐标控制基点,在岩溶隧道点云数据获取时应用三维激光扫描仪和地质罗盘相互配合进行简单、迅速的定位[13]。扫描操作:架设三脚架时,先按照测平的水泡,不断调整脚支架直至将三脚架顶部调整至水平,使得脚架固定好。利用标靶进行拼接,根据所测隧道的特点及隧道内的环境,确定测站数为2个,设置4个标靶,并且使得扫描仪在两个测站位置都能观测;启动扫描软件,设置亮度,扫描精度,并设置掌子面区域的扫描角度,设定采集间距,对测区掌子面和标靶进行高密度扫描,获取标靶和掌子面点云数据,并基于标靶进行拼接,得到测区完整点云图,如图1所示。

图1 点云数据的获取
2.2 岩溶隧道掌子面点云数据滤波、插值
三维激光扫描系统采集的数据为点云数据,点云数据首先处理滤波、插值。
为了验证该组合插值方法在基于三维激光扫描技术的岩溶隧道岩体信息——岩石产状获取中的有效性。根据式(7)的推导过程设置插值计算流程,建立组合插值模型的步骤如图2所示。
1)首先建立变异函数模型。按照原始数据直方图对数据的结构进行分析,剔除点云数据中的瑕点,绘制试验变异函数图形;再采用球状和高斯模型拟合变异函数解析式
2)调用Matlab软件工具箱中的适应度函数,并带入式(6)中的权重系数,完成基于组合模型的岩溶隧道掌子面的点云数据的插值。
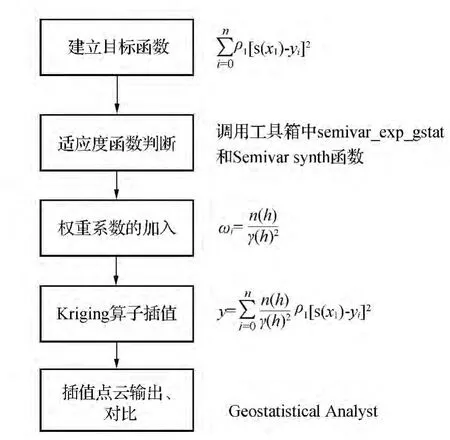
图2 建立组合插值模型的流程
2.3 岩溶隧道掌子面岩体信息——结构面产状
将点云数据应用建立的组合插值理论处理后,导入到HDS-4400三维激光扫描仪自身携带的软件I-site中,进行岩石结构面的辨别。原理:首先将要获取产状的结构面点云数据选中,并将按选中结构面点云拟合成一个平面——结构面。而后得出该平面的参数方程,即平面方程式中:A,B,C,D 均为参数,其中A,B,C 组成平面法向量坐标n,即n={A,B,C}。在扫描点云坐标系统中y轴对应工程坐标中的N(北)方向,x轴对应E(东)方向,z轴为垂直方向,由此可求出相对准确的结构面信息产状(见图3)。


图3 选中、识别的结构面
2.4 精度的评定
经过Kriging算法和最小二乘法的组合理论插值处理后的点云,根据结构面识别的方法,识别出其中30个结构面,并且解译出其结构面的产状,与单一的最小二乘法进行插值得到结果和罗盘获取的岩体信息—结构面产状进行了对比,见表1。

表1 组合模型、最小二乘法和罗盘获取产状对比
根据表1中三种岩体信息,分别绘制倾向、倾角对比图,见图4。

图4 倾向、倾角对比图
由文献[15,16]统计的罗盘测量倾向和倾角的中误差可知,其值分别为4°和3°,然后根据测量学中限差分析可知,其值一般取中误差的2倍或3倍作为限差,则由此确定罗盘一次测量倾向和倾角的限差值为12°和9°。并将两种方式解译的30组结构面产状与罗盘获得的结果进行比较,并依据式9计算出倾向、倾角的中误差。

通过计算可知,单一的最小二乘法插值处理后的中误差:m单-倾角=±2.54,m单-倾向=±2.94,基于Kriging算子和最小二乘法组合的插值方式插值结果 的 中 误 差:m组合-倾向=±1.586,m组合-倾角=±1.455。对比结果表明:两者之差均≤8°,合限率为100%,则基于三维激光扫描技术获取的点云数据,经最小二乘法和组合方法解译近似结构面的产状都满足限差要求,证明了组合方式解译出的结构面信息—岩体产状是有效的。
再将罗盘获得的产状值记为“实际监测值”,并计算出利用三维激光扫描仪获得的结构面信息—岩体产状时采用的不同差值方法:单一最小二乘法、组合模型与“实际监测值”的误差值,绘制成倾向和倾角的误差分布图,见图5。
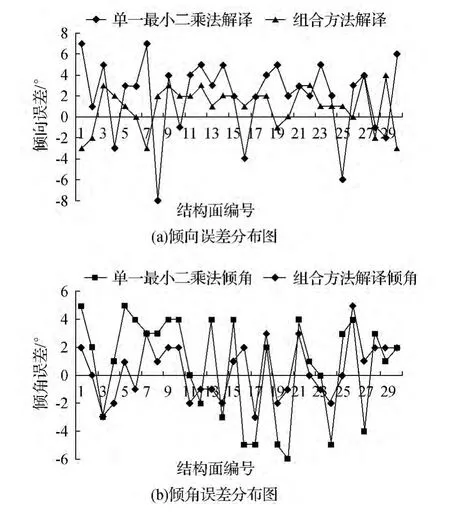
图5 倾向倾角误差分布图
由图5可知,对于沪昆铁路客运专线雪峰山隧道—岩溶隧道选取里程内岩体,在应用三维激光扫描技术获取岩体表面信息—结构面产状的过程中,基于Kriging算子和最小二乘法组合的插值方法解译获取的结构面产状的精度要比单一的最小二乘法获取的结果高,能够反映出三维激光扫描技术在岩溶隧道获取岩体信息—结构面产状时的长距离、高效性和精度高的特点,能够为岩溶隧道的施工提供一定的指导作用。
3 结 论
1)三维激光扫描技术突破了人工罗盘接触式获取岩溶隧道掌子面岩体信息——结构面产状的传统方式,可以快速、有效、全面获取结构面的信息。
2)基于三维激光扫描技术的Kriging算子和最小二乘法组合的插值方法可以快速解译获取结构面产状,结合传统单一的最小二乘法解译,通过与人工罗盘获取结构面产状的方法对比验证,证明方法的正确性和有效性。
3)在通过三维激光扫描技术获取岩溶隧道掌子面岩体信息—结构面产状时,基于Kriging算子和最小二乘法组合的插值处理方法比单一的最小二乘法的插值方法精度更高,能够更加有效的、精确地获取结构面产状,可以更好的指导隧道的建设、施工,提高施工效率。
[1] 田志宇,李海清,钟勇.岩溶隧道处治方案的支护参数的选取[J].现代隧道技术,2011,10(5):82-86.
[2] 丁延辉,邱冬炜.基于地面三维激光扫描数据的建筑物三维模型重建[J].测绘通报,2010(3):55-57.
[3] 曹先革,杨金玲,司海燕,等.地面三维激光扫描点云数据精度影响因素及控制措施[J].测绘工程,2014,23(12):5-7.
[4] 张洪栋,刘翔,时振伟.影响地面三维激光扫描仪数据质量的因素分析[J].测绘与空间地理信息,2014,37(2):183-186.
[5] 薛晓轩.基于三维激光扫描的文物保护管理系统的建立[J].测 绘与空 间地理信息,2014,37(2):99-101,105.
[6] 郝刚,胡鑫凡,岳朝林.一种三维激光扫描点云数据的预处理方法[J].测绘科学,2014,39(7):90-93.
[7] 严剑锋,邓喀中,邢正全.基于最小二乘拟合的三维激光扫描点云滤波[J].测绘通报,2013(5):43-46.
[8] ZHANG Keqi,CHEN Shuching,Whit man D,et a1.A Progressive Mor phological Filter for Removing Nongroud Measurements from Airborne Lidar Data[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41(4):872-88.
[9] 汪奇生,杨德宏.顾及系数矩阵常数列的总体最小二乘迭代解法[J].测绘工程,2014,23(7):38-40.
[10]刁鑫鹏,吴侃.基于Kriging算法与曲面拟合的三维激光扫描点云数据插值研究[J].大地测量与地球动力学,2012,2(1):110-114.
[11]徐亦唐.基于最小二乘法的曲线拟合及其在Matlab中的应用[J].电子世界,2013(10):102-103.
[12]严华雯,吴健平.加权最小二乘法改进遗传克里金计算机技术与发展与研究[J].计算机技术与发展,2012,3(3):92-95.
[13]董秀军,黄润秋.三维激光扫描技术在高陡边坡地质调查中的应用[J].岩石力学与工程学报,2006,12(Z2):112-116.
[14]邵才瑞,印兴耀.储层属性的遗传神经克里金插值方法及其应用[J].中国石油大学学报:自然科学版,2007,31(5):35-39.
[15]王凤燕,陈剑平.基于VirtuoZo的岩体结构面几何信息获取研究[J].岩石力学与工程学报,2008,27(1):169-175.
[16]王凤燕,陈剑平.基于数字近景摄影测量的岩体结构面几何信息解算模型[J].吉林大学学报:地球科学版,2012,42(6):1839-1842.
