天文经纬度归心实用算式推证
2015-03-28苏明晓赵军喜王玉峰
苏明晓,包 欢,赵军喜,王玉峰
(1.96633部队,北京 100096;2.信息工程大学 地理空间信息学院,河南 郑州450052;3.92292部队,山东 青岛 266405)
1 天文经纬度归算至标志中心算式的推证
1.1 归心计算式的推证过程
图1中设C为测站,天文经纬度为λ0,φ0。Z为库房测试间的地面标志中心,天文经度和纬度分别为λ,φ。归心的目的是将测站天文经纬度归算为标志中心的经纬度,需测定归心元素:d为测站C到标志中心Z之间的水平距离,α为CZ方向的方位角,由正北起算。CK为C点的平行圈,在球面三角形CZK中有
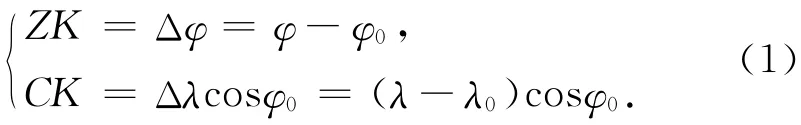
球面三角形CZK相对较小,可视作平面三角形,所以
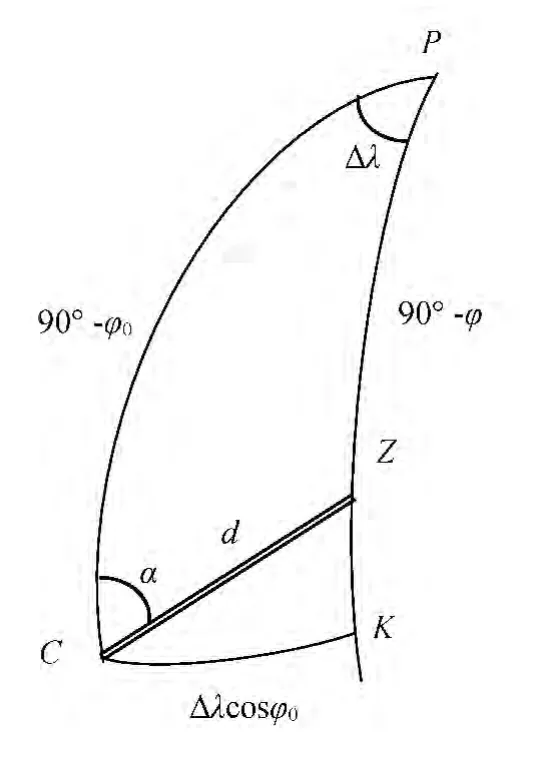
图1 测站归心

因此
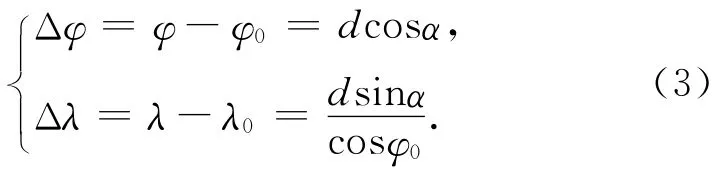
第一等式右边应乘以ρ/M0,第二等式右边应乘以ρ/N0,得到

其中ρ=206 265是角秒与弧度的换算常数;M0和N0为C点的子午圈曲率半径和卯酉圈曲率半径。在椭球测量学中[2]
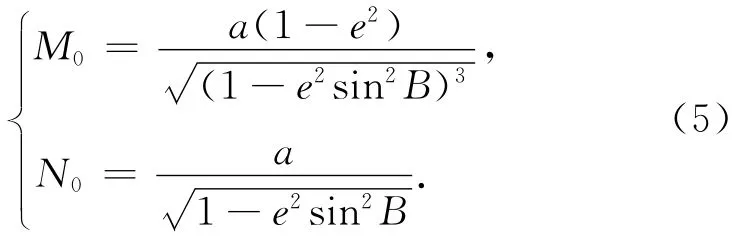
式(5)中a是参考椭球的长半轴,e2是由参考椭球基本元素导出的常数,B是测站点的大地纬度。于是得到精密的天文经纬度归心计算式
然而,国际米原器的准确度只有0.1微米,并且难以复现,容易损坏,随时间会有缓慢的变化。所以,随着科学技术的发展,用自然米取代实物米就成为了一个必然趋势。
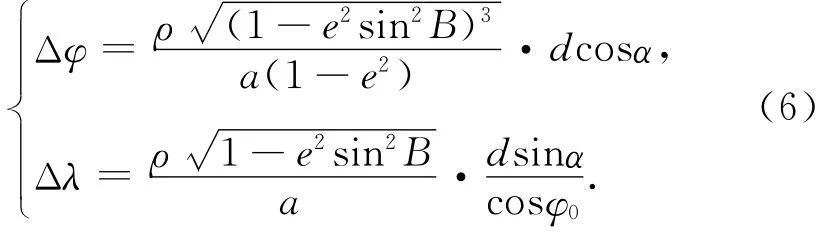
该式在一些文献中存在不同形式的谬误,数据处理人员在使用时务必注意。
由式(3)知测试间地面标志中心点的天文经纬度
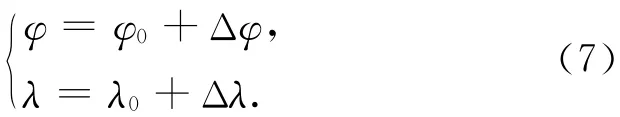
1.2 天文经纬度归心计算式中变量特点
分析式(6)中的变量:d,α和φ0是测站点的观测数据,随测站位置和实际条件而变化;ρ,a和e是(与参考椭球有关的)常数;B随测站位置的变化而变化,影响归心计算结果。在其它参数和变量确定不变的前提下,分析归心元素d,α对归心计算结果的影响:
1)d越大,Δφ和Δλ的绝对值也越大。
2)在α=0°或180°时,cosα绝对值最大为1,Δφ的绝对值也最大;sinα绝对值最小,Δλ的绝对值也最小为0。
3)在α=90°或270°时,cosα绝对值最小,Δφ的最小绝对值为0;sinα最大绝对值为1,Δλ的绝对值也最大。
2 天文经纬度归心计算实用公式的设计
2.1 天文经纬度归心计算实用公式的设计
我国自2008年7月1日起启用2000国家大地坐标系,归心计算使用的椭球参数是确定不变的[3-4]。不妨构建常数
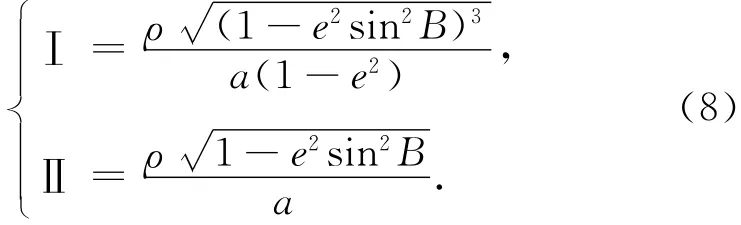
我国领土的地理纬度大体在北纬3°~55°之间,随着纬度B增大,sin B增大,(1-e2sin2B)减小,即常数Ⅰ和Ⅱ随B增大而减小。为获得有较好代表性的常数Ⅰ和Ⅱ的数值,分别取B=3°和B=55°,将2 000国家大地坐标系的椭球参数a=6 378 137 m、常数e2=0.006 694 380 022 9和ρ一并代入式(8)[5];得到3°和55°处常数Ⅰ、Ⅱ的数值,取其均值作为常数Ⅰ、Ⅱ的结果[6]

于是式(6)简化为

这就是适于我国境内使用的天文经纬度归心计算简化公式。Δφ和Δλ计算结果的单位分别是角秒和时秒。
2.2 归心元素测量精度的数学分析
式(10)中观测值d和α相互独立,其测量的中误差为md和mα,根据误差传播定律,Δφ和Δλ的误差mΔφ和mΔλ应为[7]
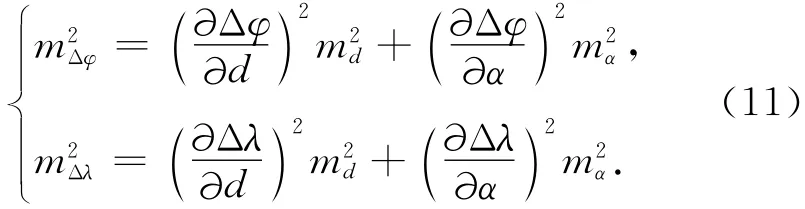
进一步计算偏导数
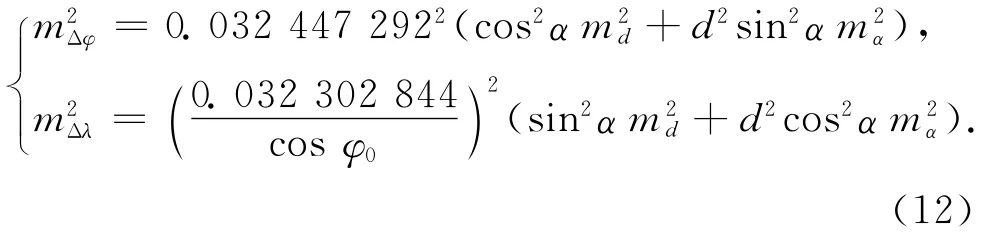
解得
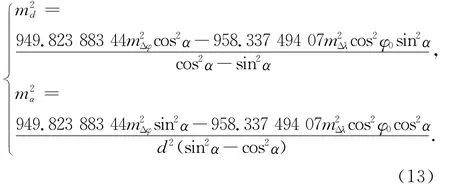
可见在Δφ和Δλ精度既定的情况下,归心元素的测量精度与测站点天文纬度φ0有关,且随偏心观测的水平距离d和方位角α的大小不同而变化,具体作业时宜根据作业条件确定归心元素的测量精度。
3 计算比对及结论
为分析归心计算式的精度,对试验数据做如下处理:
1)为保证公式的实用性,归心元素d使用近年实际数据处理作业中遇到的最大值350 m;
2为便于讨论,归心元素α分别取接近其最大值的0.1°和89.9°各两组数据;
3)大地纬度B分别取3°和55°各两组数据,以确保试验数据涵盖我国境内大部分地区;
4)天文纬度φ0与大地纬度B取值基本一致。
在使用简化天文经纬度归心式(10)计算的同时,使用精密天文经纬度归心式(6)进行比对计算。试验数据及计算、比较和统计结果见表1(为方便比较,Δλ单位也用角秒表示)。
专用工程需要的天文纬度和经度测量中误差分别是±0.5″和±0.4 s(相当于±0.6″)。
1)天文纬度和经度归心简化实用公式与精密公式计算结果最大互差分别是0.038″和0.022″,这种极值出现在我国疆域的南北两端,且小于所需天文纬度和经度测量中误差的10%。在我国中部广大地区其互差仅为测量中误差的1~2%。二者计算结果互差达到可以忽略的量级。

表1 两种天文经纬度归心计算结果比较表
2)天文纬经度归心简化实用公式与精密公式计算结果互差中误差分别是±0.02″和±0.01″,均达不到天文纬度和经度测量中误差的5%,忽略其差异不会对成果精度产生明显影响[8]。
即用简化天文经纬度归心公式计算获得的归心改正数Δφ和Δλ精度与精密计算公式相当,该式完全可以用于设备库房导航设备测试间的天文经纬度归心数据处理。
利用简化的天文经纬度归心计算实用公式,可在野外简陋环境下快速计算天文经纬度归心改正数,获取设备测试间地面标志中心点的天文经纬度;或作为归心改正精密计算结果正确性的检核手段,增强成果可靠性。
[1] 艾贵斌.导弹阵地大地测量原理与方法[M].北京:解放军出版社,2011:432-439.
[2] 郭群长,李仲勤,李辉.椭球大地测量学概论[M].成都:西南交通大学出版社,2009:50-55.
[3] 程鹏飞,成英燕,文汉江.2000国家大地坐标系实用宝典[M].北京:测绘出版社,2010:127-128.
[4] 田桂娥,宋利杰,尹利文,等.地方坐标系与CGCS2000坐标系转换方法的研究[J].测绘工程,2014,23(8):66-69.
[5] 吕志平,乔书波.大地测量学基础[M].北京:测绘出版社,2010:90-95.
[6] 中国人民解放军总装备部.GJB 6304-2008 2000中国大地测量系统[S].北京:总装备部军标出版发行部出版,2008.
[7] 孔祥元,郭际明.控制测量学[M].武汉:武汉大学出版社,2010:116-122.
[8] 隋立芬,宋力杰,柴洪洲,等.误差理论与测量平差基础[M].北京:测绘出版社,2010:40-45.
